2. 云南省无线传感器重点实验室, 昆明 650500
2. Key Laboratory of Wireless Sensor in Yunnan Province, Kunming 650500, China
现实生活中的事物都可以用复杂网络[1]模型来表示. 大数据[2]背景下, 复杂网络的规模不断变大. 研究表明, 复杂网络不仅具有小世界、无标度等特性外, 还呈现出明显的社区结构[3]. 社区结构能够更好地理解网络中的拓扑, 从而发现网络中隐藏的规律, 对网络进行预测和改造. 如社交网络分析、控制疾病传播等.
目前, 各种社区发现算法被提出并不断地改进. 其中2007年Raghavan等提出的标签传播算法[4](Label Propagation Algorithm, LPA)最典型. LPA算法因简单且具有接近线性的时间复杂度常用于处理大规模复杂网络. 由于算法中存在过多的随机策略, 导致社区发现的准确性和稳定性较差. LPA算法因此得到不断改进. 如Barber等提出基于模块度目标函数标签传播算法(LPAm)[5]来防止将网络划分成一个社区, 但导致形成大量的小社区影响划分结果. 赵卓翔等提出基于标签影响值的社区发现算法(LIB)[6]来提高社区发现的质量, 但计算时需要用到边的权重, 而网络中边的权值很难确定. 随着网络规模不断增大, 改进算法也面临巨大的挑战.
本文利用节点的K-Shell[7]指数对原始网络进行预处理: 去除边缘层的节点, 赋予核心层节点标签. 然后利用改进算法对预处理网络进行标签传播. 网络的预处理在一定程度缩小了网络规模, 减少了初始标签个数, 加快了算法的收敛速度. 同时改进算法降低了随机性, 提高了算法的准确性和稳定性.
1 LPA算法分析 1.1 LPA算法标签传播算法用给定节点的标签信息来对未给定标签的节点的标签进行预测. 初始时, 网络中每个节点分配一个唯一的标签; 其次, 随机选择节点进行标签更新; 根据式(1)选择其相邻节点中出现频率最高的标签. 经过若干次迭代, 网络中拥有相同标签的节点构成一个社区.
| ${c_x}(t) = \arg \max \mathop \sum \limits_{j \in {N^l}(x)} {w_j}$ | (1) |
LPA算法中存在着大量的随即策略. 初始时每个节点分配一个标签, 形成一些小的、零散的社区, 导致有意义的社区不能形成, 同时放慢了收敛速度; 节点的更新顺序是随机的, 导致最终的结果多样性, 稳定性自然而然降低; 在更新过程中, 忽略节点间重要性的差异, 影响力小的节点有可能反过来影响具有较大影响力的节点, 导致结果准确性降低.
随着大数据时代的到来, 使得可供研究的数据越来越丰富. 复杂网络规模不断增大, 网络中节点数不断增加. 标签传播算法除现有的准确性和稳定性问题外, 大规模复杂网络导致算法的运算量加倍增加, 收敛速度减慢, 失去了原始算法高效的特点.
2 改进的KLPA算法 2.1 网络分层在人际关系网中, 人与人间的影响力是有差异的. 有人是起决定性作用的“领导”, 而有人则是无关紧要的“路人”.同理, 复杂网络中节点间影响力[8]亦如此. 节点的影响力与节点在网络中所处的位置有关: 通常, 影响力大的节点处在网络中的核心位置, 相反影响力小的节点处在网络中的边缘位置. K核分解可以很好地衡量出节点在网络中的所处的位置, 将网络划分成核心—边缘的层次, 衡量节点在全局重要程度.
K核分解(K-core Decomposition): 将网络中所有度为1的节点删除, 删除后若还有度为1的节点, 则继续删除度为1的节点, 直到网络中剩余节点的度都大于1为止, 删除节点的K值为1. 同理K值等于2的节点亦如此, 依次类推. 分解过程结束后, 每个节点的K值都被确定.
K值将网络中的节点划分到不同的层, 即节点在网络中所处的位置.
定义1. 核心层: 网络中处于核心位置的节点, 它们在网络中起决定性用. 核心层节点的重要性往往大于其它层的节点.
| $core(i) = node(k = \max (k))$ | (2) |
定义2. 边缘层: 网络中处于边缘位置的节点, 作用相当于网络中的“路人”. 边缘层节点的影响力是整个网络中最小的.
| ${{brink(}}i{{)}} = node(k = \min (k))$ | (3) |
网络分层对改进标签传播算法具有很大的帮助, 尤其针对算法的初始化阶段.
2.2 预处理阶段分析LPA的结果发现, 节点的标签种类数远远少于初始标签的种类数, 大多数标签随着迭代更新而消失. 最终剩余的标签通常是初始时影响力较大的节点的标签, 它们在传播中起主导作用. 这些节点往往是每个社区的中心.
网络中具有较大影响力的节点通常处于核心层, 它们的标签决定着社区划分结果. 初始时只赋予核心层的节点标签, 其余层节点不赋予标签. 可以大大减少初始的标签, 避免出现零散、小的社区, 有助于提高划分的准确性.
网络中存在一些“无关紧要”的节点, 其影响力相对较小, 如边缘层节点. 在传播过程中它们对邻居节点标签并无影响, 只是单纯地服从更新. 但随着网络规模的增大, 边缘层节点的数量急剧增多. 它们不断地重复更新不仅增加了运算量, 还放慢了收敛速度.
如果将边缘层节点去除, 不仅减少节点个数, 缩小网络的规模, 对算法的结果几乎无影响, 从而提高了算法的有效性.
预处理阶段: 仅赋予核心层的节点标签, 同时去除边缘层节点, 对预处理网络进行标签更新.
2.3 更新阶段预处理阶段从网络整体出发简化初始网络. 而更新阶段, 则发生在网络的局部. 更新节点的标签与其邻居节点的标签有关, 它与邻居节点的影响力大小相关. K核分解是全局刻画节点的影响力, 并不能充分体现节点的局部影响力.
Kitsak等认为度能刻画节点周围局部特征[9]. 因此引入归一化度值作为节点的局部影响力.
| $lo(i) = \frac{{d(i)}}{{\max \left\{ {d(j)|d(j \in V)} \right\}}}$ | (4) |
为更加全面地衡量节点的影响力, 将全局影响力k值和局部影响力lo相结合, 得出节点在网络中的综合影响力.
| $IN(i) = k(i) + lo(i)$ | (5) |
原始算法中选择其邻居节点中出现频率最高的标签作为更新节点的标签. 更新节点的标签除与邻居节点的影响力大小相关外, 还与邻居中出现的标签个数相关. 选择其邻居中影响力最大的标签.
| $influence\left( l \right) = \sum\limits_{m \in {N^l}\left( x \right)} {IN\left( m \right)} $ | (6) |
| ${c_x} = \arg \max influence(l)$ | (7) |
当更新节点的邻节点都没有标签时, 则选择下一节点进行更新; 如果邻居节点有标签时, 则根据式(7)选择其中具有最大影响力的标签.
更新时确定的节点更新顺序可有效降低随机性. 预处理仅赋予核心层节点标签, 标签分布在网络的中心. 为提高更新效率, 节点应从网络中心向边缘(节点影响力降序顺序)大致有序进行更新.
2.4 后处理阶段预处理网络的社区划分结束后, 对边缘层节点的标签进行确定. 由于边缘层节点的影响力相对较小, 极易受到其邻居中影响力大的节点影响. 因此其标签由邻居中影响力最大的节点的标签所决定.
| ${C_x} = \arg \max IN(i)$ | (8) |
最后拥有相同标签的节点在同一个社区.
算法分3个步骤:
(1)预处理阶段
网络进行K核分解, 划分成核心-边缘层. 赋予核心层节点标签, 并去除边缘层节点.
(2)标签更新阶段-预处理网络
计算节点的综合影响力, 按影响力降序顺序依次更新节点;
依据式(7)选择标签作为更新节点的标签;
若节点标签不再变化, 算法结束.
(3)后处理阶段
边缘层节点的标签, 根据式(8)选择其邻居中具有最大影响力的节点的标签.
最后, 具有相同标签的节点划分到同一个社区.
相对于原始算法, 改进算法的预处理阶段缩小了网络规模, 减小了更新时节点的运算量改进的更新策略降低了随机性, 加快了算法的收敛速度.
3 实验与分析仿真工具MATLAB(matlab2012a, Win 7 64位, 4 GB内存). 为验证算法的有效性, 实验数据采用真实网络和LFR人工合成网络. 算法中存在随机性, 对实验运行1000次后取均值.
3.1 真实网络海豚网络是由栖息在新西兰的一个宽吻海豚群体所构造出的关系网(含2个家族).节点代表海豚, 边表示两个海豚之间接触频繁, 网络由62个节点和159条边组成. 采用改进算法对网络进行社区划分, 分析过程及结果如下所示.
网络被划分为4层, 边缘层的节点K=1, 核心层节点K=4.将边缘层节点去除后, 得到一个53个节点和150条边组成的新网络. 节点数减少14.5%, 边减少5.6%. 图1为算法的划分结果. 网络被划分为两大社区, 与实际社区对比, 节点的划分准确率为98%.为充分了解算法性能, 将改进算法与LPA和LPAD算法进行实验对比, 具体的实验数据结果如表1所示.
社区划分方式即社区的划分种类数, 数值越大, 说明社区划分结果越分散、不集中, 算法的稳定性也就越差. LPA划分方式为153种, LPAD为11种, KLPA仅为1种. 比较社区大小发现, LPA和LPAD算法会出现节点个数分别为2或5的零散、小社区, 与真实的社区情况不相符. 规范化交互信息(NMI)的值越大, 说明社区划分结果与实际社区越一致. 对比发现LPA的NMI值最低, 说明其准确性较低. LPAD的准确性得到提高, 而KLPA的准确性最高. 迭代次数越小表明算法收敛越快. KLPA算法的迭代次数最小, 加快了收敛速度, 依然保持高效的特点.

|
图 1 海豚网划分图 |
| 表 1 海豚网数据结果 |
同时还对其他网络进行分析—Karate网络、Football联赛网络、Polbooks联赛网络, 采用模块度函数Q值、标准化互信息NMI值和迭代次数来对比算法性能, 结果表2所示. 由表2可知KLPA算法的Q值和NMI值大于LPA和LPAD算法, 说明KLPA算法获得的社区质量相对较高, 社区划分的准确性也高于其他两种算法. KLPA算法的迭代次数明显低于LPA和LPAD算法, 算法的收敛速度加快.
| 表 2 实验网络结果 |
3.2 LFR网络
LFR基准网络常用来测试社区发现算法的性能. 当网络中社区结构明显时(0<mu< 0.45时), LPA算法的划分效果很好. 随着mu增大(mu> 0.45时), 网络社区结构变得越来越复杂, 社区划分效果也就变得较差. 针对社区结构复杂这种情况, 对算法的性能进行比. 网络参数设置: G1:N=1000, K=15, kmax=50, cmin=20, cmax=50, G2: N=2000, K=15, kmax=50, cmin=20, cmax=50. mu取值在0.4–0.65之间.
从图2可知, 无论网络中节点个数为1000或2000, 当网络结构变得复杂时, 两种算法的准确性均有所下降, 但KLPA算法的NMI值明显大于LPA算法. 说明当网络结构较复杂时, KLPA算法的社区发现准确性相对较高, 具有比LPA算法更好的性能. 当mu增大到0.65时, 网络中的社区结构变得模糊. 各社区间连接更加紧密, 相互渗透, 节点间的差异变小, 算法很难发挥作用, 准确性大大降低, 两种算法失效.

|
图 2 LFR网络NMI对比 |
同时对两种算法的迭代次数进行对比发现, KLPA算法的迭代次数远远小于原始算法. 说明改进算法加快了收敛速度, 提高了效率. 当mu>0.65时, LPA算法失效, 迭代次数也就失去意义, 如图3所示.
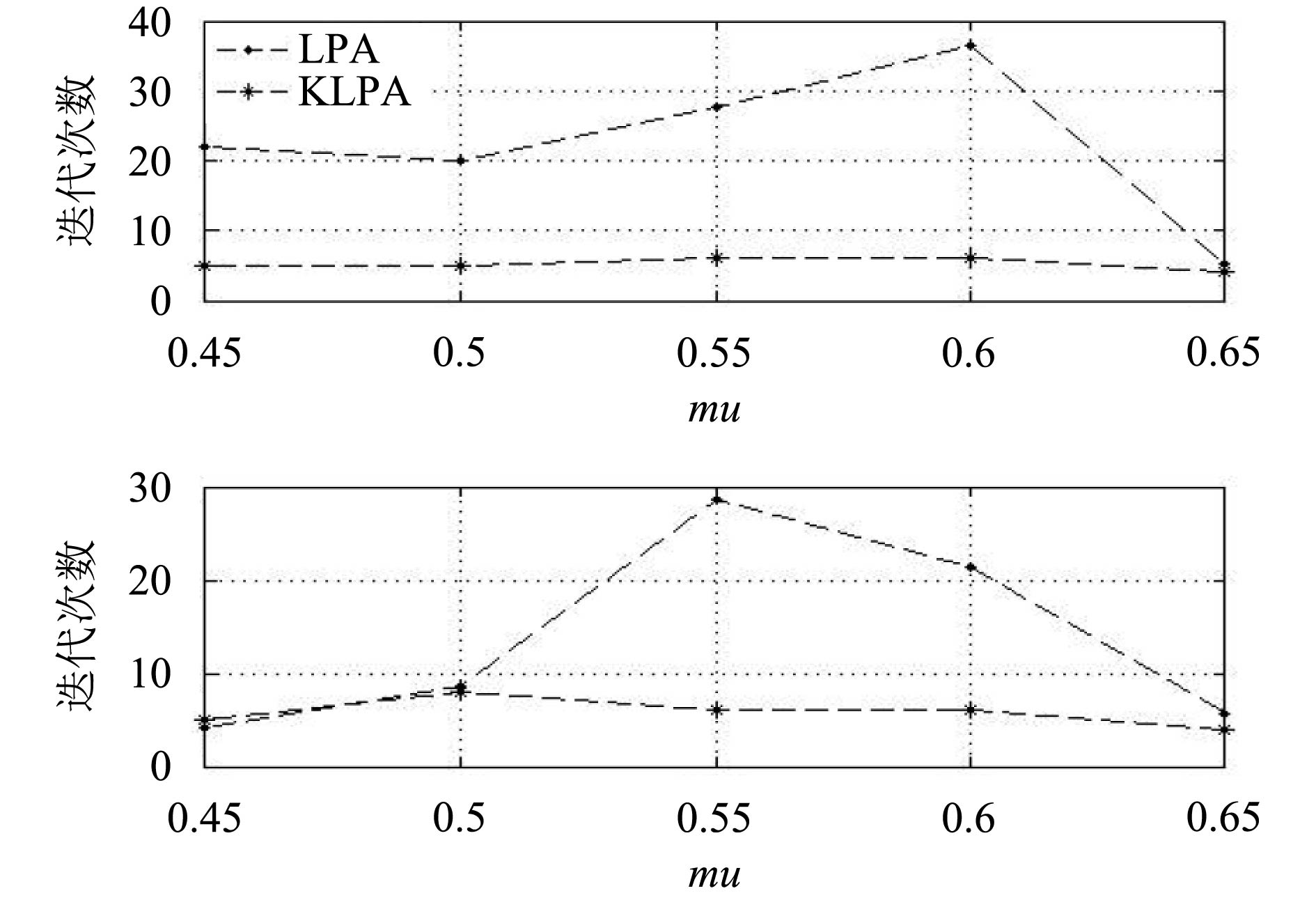
|
图 3 迭代次数对比 |
4 结论
随着网络规模的增大, 现有算法除准确性和稳定性问题外, 算法的收敛速度也减缓. 本文从整体上利用K-Shell指数将网络分层, 一定程度上缩小网络规模. 并在局部对算法的更新策略加以改进. 仿真实验证明KLPA算法不仅可以缩小网络规模, 并能提高社区划分的准确性和稳定性. 加快算法的收敛速度.
| [1] |
刘涛, 陈忠, 陈晓荣. 复杂网络理论及其应用研究概述. 系统工程, 2005, 23(6): 1-7. |
| [2] |
周涛. 网络大数据——复杂网络的新挑战: 如何从海量数据获取信息?. 电子科技大学学报, 2013, 42(1): 7-8. |
| [3] |
刘发升, 罗延榕. 基于多种群遗传算法的复杂网络社区结构发现. 计算机应用研究, 2012, 29(4): 1237-1240. |
| [4] |
张俊丽, 常艳丽, 师文. 标签传播算法理论及其应用研究综述. 计算机应用研究, 2013, 30(1): 21-25. |
| [5] |
Barber MJ, Clark JW. Detecting network communities by propagating labels under constraints. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 80(2 Pt 2): 026129. |
| [6] |
赵卓翔, 王轶彤, 田家堂, 等. 社会网络中基于标签传播的社区发现新算法. 计算机研究与发展, 2011, 48(S2): 8-15. |
| [7] |
顾亦然, 王兵, 孟繁荣. 一种基于K-Shell的复杂网络重要节点发现算法. 计算机技术与发展, 2015, 25(9): 70-74. |
| [8] |
任晓龙, 吕琳媛. 网络重要节点排序方法综述. 科学通报, 2014, 59(13): 1175-1197. |
| [9] |
Kitsak M, Gallos LK, Havlin S, et al. Identification of influential spreaders in complex networks. Nature Physics, 2010, 6(11): 888-893. DOI:10.1038/nphys1746 |
 2018, Vol. 27
2018, Vol. 27


