近年来快节奏的生活方式引发的亚健康人群数激增现象, 引起人们对养生学的重视, 饮食营养成为突破口, 现存的西医营养学过分注重化学成分(如卡路里、碳水化合物等)对人体的影响, 割裂了人体统一和谐的身体系统^[1], 而中医营养学从人体整体把握饮食对人的影响, 已成为主流. 中医营养学起源于中医药学“药食同源”, 人工流传记载为主, 其中大量营养属性值存在元素多元化、数据缺失、数据值模糊的问题, 规则提取后的知识冗余度高且存在冲突项.

应用粗糙集理论进行规则提取可以从已知的各种不完备的数据信息中快速获取知识和规律, 包括属性约简和值约简两个步骤. 对这个问题的探索已经存在一些方法, 文献[2]提出了基于加权变精度容差粗糙集模型; 文献[3]提出了一种基于粗糙集理论的值约简算法; 文献[4]提出了改进不可区分关系的值约简算法; 文献[5]提出一种基于差异关系的变精度粗糙集知识约简算法; 文献[6]等提出了基于广义优势决策函数的决策规则获取方法; 文献[7]改进了邻域粗糙集模型, 并将其应用到故障诊断规则提取中. 然而在分析现有规则提取的算法及数据特点时发现, 算法注重对决策属性之间的关系提取, 对得到矛盾规则不具备良好的处理力能.

因此, 引入具有噪声容忍机制的决策粗糙集模型, 使用α-正域约简启发式算法约简属性, 克服无关属性对决策值的干扰. 在决策表值约简过程中, 引入可覆盖关系和活跃值等概念, 构建待定矩阵和覆盖矩阵, 提出概率覆盖模型, 处理矛盾的知识规则, 得到普适性较高的规则.

1 决策粗糙集模型

决策粗糙集^[8]引入了Bayes风险决策理论, 使其在不确定性知识获取和数据处理中具有更加可靠的理M论依据和语义解释^[9], 是对经典Pawlak粗糙集理论模型缺乏容错能力的概率拓展.

定义1. 给定菜谱信息系统 $S = \left( {U,C \cup D,f} \right)$ , U为菜谱标号, C和D分别为中医营养学属性集与是否养肠胃的决策属性集, f是信息函数, $X \subseteq U$ , 设行为集合 $\{ {a_P},{a_B},{a_N}\} $ 表示接受菜谱x为养肠胃菜谱的决策行为、待定决策行为、拒绝决策行为, ${\lambda _{PP}},{\lambda _{BP}},{\lambda _{NP}}$ 表示 $x \in X$ 时采取行为 ${a_P},{a_B},{a_N}$ 所产生的风险损失, ${\lambda _{PN}},{\lambda _{BN}},{\lambda _{NN}}$ 表示 $x \in \neg X$ 时采取行为 ${a_P},{a_B},{a_N}$ 所产生的风险损失. 根据贝叶斯最小风险决策原则, 将其划分为三个部分, 正域 ${{POS}}\left( X \right)$ 、边界域 ${{BND}}\left( X \right)$ 、负域 ${{NEG}}\left( X \right)$ , 决策粗糙集有如下决策规则:

1) if $P\left( {X{{|}}{{\left[ x \right]}_C}} \right) \ge \alpha ,x \in {{POS}}\left( X \right)$

2) if $\beta < P\left( {X{{|}}{{\left[ x \right]}_C}} \right) < \alpha ,x \in {{BND}}\left( X \right)$

3) if $P\left( {X{{|}}{{\left[ x \right]}_C}} \right) \le \beta ,x \in {{NEG}}\left( X \right)$

其中, $\left\{ {\begin{array}{*{20}{c}}{\alpha = \displaystyle\frac{{{\lambda _{PN}} - {\lambda _{BN}}}}{{{\lambda _{BP}} - {\lambda _{PP}} + {\lambda _{PN}} - {\lambda _{BN}}}}}\\{\beta = \displaystyle\frac{{{\lambda _{BN}} - {\lambda _{NN}}}}{{{\lambda _{NP}} - {\lambda _{BP}} + {\lambda _{BN}} - {\lambda _{NN}}}}}\end{array}} \right.$ , 且 $\alpha,\; \beta \in \left[ {0,1} \right]$ .

由此, 定义决策粗糙集的下、上近似分别为:

$\underline {apr} _C^{\left( {\alpha ,\beta } \right)}\left( {{X}} \right) = \{ x \in U|P\left( {X|{{[x]}_C}} \right) \ge \alpha \} $

(1)

$\overline {apr} _C^{\left( {\alpha ,\beta } \right)}\left( X \right) = \left\{ {x \in U|P(X|{{[x]}_C}) > \beta } \right\}$

(2)

其中 $P\left( {X{{|}}{{\left[ x \right]}_C}} \right) = \frac{{\left| {X \cap {{\left[ x \right]}_C}} \right|}}{{\left| {{{\left[ x \right]}_C}} \right|}}$ , $\left| \cdot \right|$ 表示集合中元素的基数, ${\left[ x \right]_C}$ 为x在属性集C下的等价类.

定义2. $S \!=\! \left( {U,C \cup D,f} \right)$ 为一个菜谱决策表, $\alpha \!\in \!\left[ {0,1} \right]$ , 若属性子集 $B \subseteq C$ 满足下面2个条件:

(1)正域非减性, $|{{POS}}_B^\alpha \left( D \right)| \ge |{{POS}}_C^\alpha \left( D \right)|$ ;

(2) 属性独立性, 对任意 $\alpha \in B$ ,

$|{{POS}}_{B - \left\{ a \right\}}^\alpha \left( D \right)| < |{{POS}}_B^\alpha \left( D \right)|$

称属性子集B为属性全集C的一个决策粗糙集α-正域约简^[10].

定义3. 设 $S = \left( {U,C \cup D,f} \right)$ 为一个菜谱决策表, $\alpha \in \left[ {0,1} \right]$ 为条件概率阈值, $a \in C$ 为单个属性, 则属性a的α-正域全局重要度^[11]定义为:

$\gamma _a^{{\alpha }} = \frac{{\left| {{{POS}}_{\left\{ a \right\}}^{{\alpha }}\left( {{D}} \right)} \right|}}{{\left| U \right|}}$

(3)

2 基于决策粗糙集的概率覆盖模型

本节将建立基于决策粗糙集的概率覆盖模型, 解决中医学数据噪声产生的规则矛盾现象.

2.1 属性约简

原决策表中过多的不重要属性会影响规则提取的有效性, 因此, 本文采用决策粗糙集α正域约简算法^[11]对属性进行约简. 基于决策粗糙集的属性约简引入了决策损失函数确定阈值参数, 改进粗糙集零错误容忍率的局限性. 调整α的取值对属性重要度排序, 由专家确定最优属性组合模型, 进而确定α取值.

2.2 值约简

从决策表中得到的规则不一定是完全正确的, 原因有二: 一是上百年的中医传承记载, 样本数据本身可能含有矛盾信息, 即条件相同但决策不同; 二是营养数据离散化过程中, 由于菜谱中医属性值是计算求和所得, 忽略各原料之间相互作用, 因此属性程度概念模糊, 分类划分可能导致误差. 从而归纳得到的知识矛盾性大, 准确率低, 鲁棒性弱, 因此, 在决策表值约简过程中, 引入可覆盖关系和活跃值概念, 构建覆盖矩阵.

定义4. $S = \left( {U,C \cup D,f} \right)$ 为一个菜谱决策表, x_i, ${x_j} \in U \times \left( {C \cup D} \right)$ , $a_i^S$ 、 $a_j^S \in C\left( {i \ne j} \right)$ 分别表示在决策表中任意两个不相等的样本对应的属性值. 缺省集合 $T_{{a_i}}^S = \left\{ {{x_i} - a_i^S} \right\}, $ $T_{{a_j}}^S = \left\{ {{x_j} - a_j^S} \right\}$ 表示在决策表S中x_i和x_j去掉 $a_i^S$ , $a_j^S$ 后剩余的数据集合:

$T_{{a_i}}^S\underline \cup a_i^S = {x_i}$

$T_{{a_j}}^S\underline \cup a_j^S = {x_j}$

$\underline \cup $ 表示 $T_{{a_i}}^S$ 与 $a_i^S$ 有序合并. 例如: ${x_i} \!=\! \{ 1,0,2,0\} $ , $a_i^S \!=\! \{ 2\} $ , $T_{{a_i}}^S = \{ 1,0,0\} $ , 有 $T_{{a_i}}^S\underline \cup a_i^S = \{ 1,0,0\} \underline \cup \{ 2\} = \{ 1,0,2,0\}$ $ = {x_i}$ .

定义5. $S = \left( {U,C \cup D,f} \right)$ 为一个菜谱决策表, d_i, ${d_j} \in {{D}}$ , 对于菜谱U中的任意两条记录x_i和x_j有:

$\left\{ {\begin{aligned}{Tol\left( {{x_i},{x_j}} \right):T_{{a_i}}^S\underline \cup {d_i} = T_{{a_j}}^S\underline \cup {d_j}}\\{\overline {Tol} \left( {{x_i},{x_j}} \right):T_{{a_i}}^S = T_{{a_j}}^S\;\& \; {d_i} \ne{d_j}}\end{aligned}} \right.$

(4)

对表中的一条菜谱记录x_i, 去掉其中的一个属性值 $a_i^S$ , 缺省集合 $T_{{a_i}}^S$ 可以决定决策属性, 说明 $a_i^S$ 不重要, 两条菜谱有相似性, 可以融合, 称x_i、x_j为可覆盖关系 $Tol\left( {{x_i},{x_j}} \right)$ ; 如果缺省集合不能决定决策属性, 称x_i和x_j为不可覆盖关系 $\overline {Tol} \left( {{x_i},{x_j}} \right)$ .

定义6. 设 $S = \left( {U,C \cup D,f} \right)$ 为一个菜谱决策表, 论域 $U = \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}$ , $C = \left\{ {{c_1},{c_2}, \cdots ,{c_m}} \right\}$ , $D = \left\{ d \right\}$ , ${x_{ij}} \in U \times C$ .

${{M}}\left( {PT} \right) = {\left( {{c_{ij}}} \right)_{m \times n}}i = 1,2,3,\cdots,m;\;j = 1,2,3,\cdots,n$

(5)

定义 ${{M}}\left( {PT} \right)$ 为待定矩阵, ${c_{ij}}$ 为矩阵元素:

${c_{ij}} = \left\{ \begin{array}{c c}?, & {T_{{a_i}}^S \ne T_{{a_j}}^S}\\*, & {Tol\left( {{x_i},{x_j}} \right)}\\{x_{ij}}, & {\overline {Tol} \left( {{x_i},{x_j}} \right)}\end{array} \right.$

(6)

其中, “*”为x_i, x_j为覆盖关系时的值, “?”为待定矩阵中待评价的值, 定义矩阵元素标 “?”为活跃值 ${b_{ij}}$ , ${x_{ij}}$ 是原决策表S的值.

定义7. 一度覆盖矩阵 ${{{M}}_{S1}}\left( {PT} \right) = \left( {U,C \cup D,f} \right)$ , ${{{M}}_{S1}}\left( {PT} \right) \supseteq \left\{ {*,{x_{ij}}} \right\}$ , 对待定矩阵 ${{M}}\left( {PT} \right)$ 的活跃值 ${b_{ij}}$ 再判定:

${b_{ij}} = \left\{ {\begin{aligned}{x_{ij}^S}&,&{T_{{b_i}}^{{{M}}\left( {PT} \right)} = \emptyset }&\;\;\;\;{\overline {Tol} \left( {{x_i},{x_j}} \right)}\\*&,&{T_{{b_i}}^{{{M}}\left( {PT} \right)} \ne T_{{b_j}}^{{{M}}\left( {PT} \right)}}&\;\;\;\;{Tol\left( {{x_i},{x_j}} \right)}\end{aligned}} \right.$

(7)

其中 $x_{ij}^S$ 代表在决策表S中的取值.

定义8. 二度覆盖矩阵 ${{{M}}_{S2}}(PT) = \left( {U,C \cup D,f,\omega } \right)$ , ${{{M}}_{S2}}\left( {PT} \right) \supseteq \left\{ {*,{{{\omega }}_{{i}}},{x_{ij}}} \right\}$ , $\omega $ 为菜谱库U中规则R所覆盖的样例数目: $\omega = {[{x_i}]_R}$ .

定义9. 三度覆盖矩阵 ${{{M}}_{S3}}\left( {PT} \right) = (U,C \cup D,f,$ $\omega ,Support,Confidence)$ , ${{{M}}_{S3}}\left( {PT} \right) \supseteq \left\{ {*,{\omega _i},{x_{ij}},{{{\psi }}_S},{{{\psi }}_C}} \right\}$ ; $\forall {x_i},{x_j} \in C \cup D$ 且满足 $\overline {Tol} \left( {{x_i},{x_j}} \right)$ , $R|{{{M}}_{S2}}\left( {PT} \right)|$ 表示矩阵 ${{{M}}_{S2}}\left( {PT} \right)$ 的规则数目.

错误覆盖率:

$\theta \left( {{x_i},{x_j}} \right) = \frac{{\left| {{{[{x_i}]}_R} - {{[{x_j}]}_R}} \right|}}{{\max \left( {{{[{x_i}]}_R},{{[{x_j}]}_R}} \right)}}$

(8)

约简力度:

${{\mu }} = \frac{{R|{{{M}}_{Sk}}\left( {PT} \right)| - R|{{{M}}_{S(k + 1)}}\left( {PT} \right)|}}{{R|{{{M}}_{Sk}}\left( {PT} \right)|}}$

(9)

其中, $k = 1,2$ .

${\left[ x \right]_C} \in U/C$ , ${\left[ x \right]_D} \in U/D$ , 得到的一个规则 $f\left( {{{\left[ x \right]}_C},C} \right) \to f\left( {{{\left[ x \right]}_D},D} \right)$ , ${\left[ x \right]_C} \cap {\left[ x \right]_D} \ne \emptyset $ .

支持度:

${{{\psi }}_S} = \left| {{{\left[ x \right]}_C} \cap {{\left[ x \right]}_D}} \right|/\left| U \right|$

(10)

置信度:

${{{\psi }}_C} = \left| {{{\left[ x \right]}_C} \cap {{\left[ x \right]}_D}} \right|/\left| {{{\left[ x \right]}_D}} \right|$

(11)

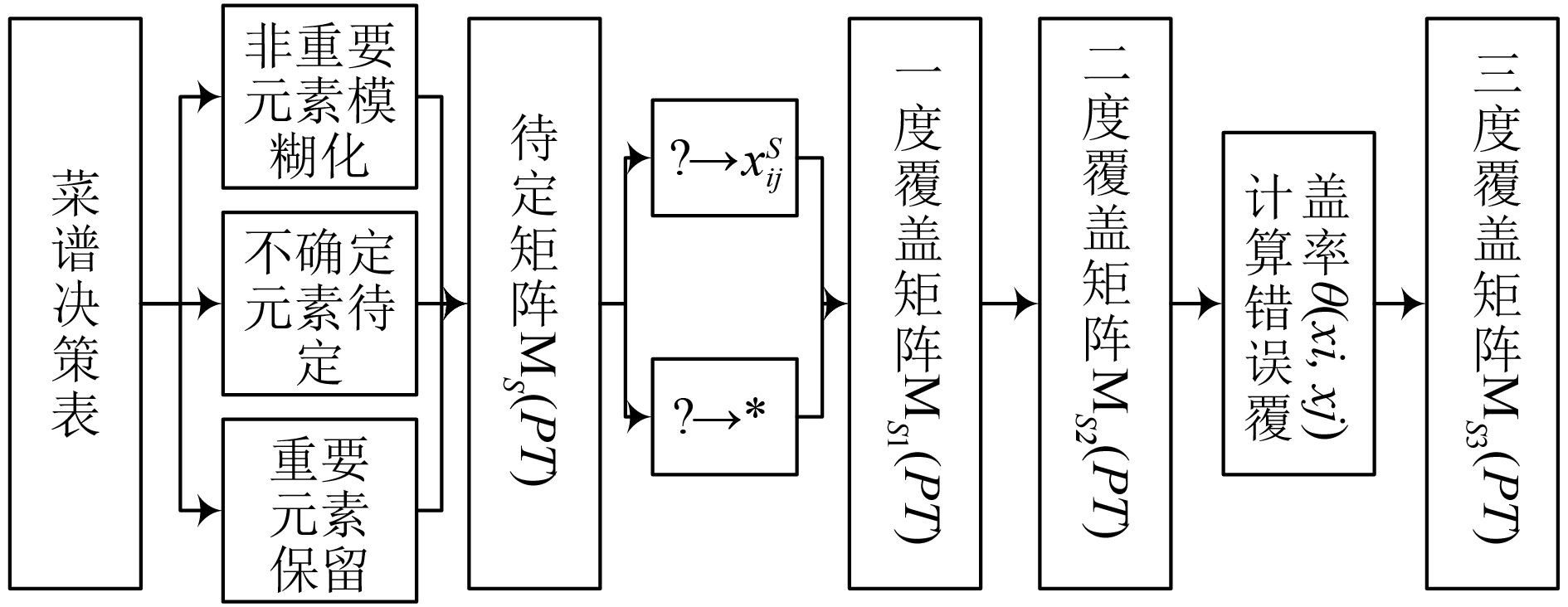
为了获得有用的规则, 需要保留重要的属性值, 删减非重要的属性值, 直至形成规则, 值约简流程图如图1所示.

首先初步对菜谱决策表进行重定义, 对表中的一条菜谱记录 ${x_i}$ , 去掉其中的一个属性值 $a_i^S$ , 校验剩下的属性集合 $T_{{a_i}}^S$ 能否决定决策属性: 如果 $T_{{a_i}}^S$ 可以独自推出决策属性, 则 ${x_i}$ 与决策表中某条记录 ${x_j}$ 构成可覆盖关系 $Tol\left( {{x_i},{x_j}} \right)$ , 即去掉 $a_i^S$ 不影响分类, 那么 $a_i^S$ 没有价值, 置为符号“*”; 如果 $T_{{a_i}}^S \ne T_{{a_j}}^S$ , 单条记录不能说明 $a_i^S$ 的重要性, $a_i^S$ 是待评价的值, 设置为活跃值, 用符号“?”代替; 如果 $T_{{a_i}}^S = T_{{a_j}}^S$ , 但决策属性值不同, 即产生冲突, 说明去掉 $a_i^S$ 就不能得到正确的规则, 那么需要保留重要属性值 $a_i^S$ . 此过程后可以得到待定矩阵 ${{M}}\left( {PT} \right)$ .

对待定矩阵 ${{M}}\left( {PT} \right)$ 中待定的活跃值b_ij再进行判定, 即可得到一度覆盖矩阵 ${{{M}}_{S1}}\left( {PT} \right)$ : 如果一条记录中, 除了活跃值, 其他属性值皆被标记为“*”, 说明在本条记录中活跃值重要, 则将其还原为原决策表的属性值; 如果记录中除去活跃值和“*”值属性, 剩下的属性组合可以推出决策条件, 则判定此活跃值b_ij不重要, 标记为“*”, 如果产生矛盾, 则说明属性值重要, 还原决策表属性值.

对一度覆盖矩阵去重处理, 并记录每条模糊规则的覆盖范围ω, 构成二度覆盖矩阵.

二度覆盖矩阵中存在矛盾项(即条件属性相同但决策属性不同), 定义错误覆盖率描述矛盾的两条规则的覆盖范围的差异程度, 认为低于所设θ的两条矛盾规则的较小项为误差, 进行舍弃. 错误覆盖率的设置: 选取在决策规则的覆盖范围较高且约简力度较大时的取值, 即可以得到覆盖样本最多且矛盾项最少的规则, 实现提取规则质量最优, 得到三度覆盖矩阵.

得到三度覆盖矩阵后, 仍存在错误覆盖率区分不开的少数冲突规则, 使用支持度、置信度进行规则约简, 置信度表示此条件属性的样例中满足此决策条件的比率, 支持度表示满足此规则的样例数占全部样本数的百分比, 比较冲突规则的支持度、置信度, 删减可信度较低的规则, 消除噪声样例造成的影响.

2.3 概率覆盖模型的算法描述

概率覆盖模型融合了决策粗糙集属性约简和值约简算法, 概率是指α正域约简中的α, 覆盖是指控制值约简中误差范围的错误覆盖率θ, 对原始矩阵不断进行精简覆盖.

2.3.1 属性约简

输入: 菜谱决策表S, 给定的概率阈值α

输出: 营养属性约简集R

(1)令初始约简属性集 $\scriptstyle R = \emptyset ;$

(2)根据式子(3)计算每个属性的α-正域重要度 $\scriptstyle \gamma _a^{{\alpha }}$ ;

(3)将属性按照重要度由大到小排列, 令其为P;

(4)在 $\scriptstyle\left| {{{POS}}_R^\alpha \left( D \right)} \right| < \left| {{{POS}}_C^\alpha \left( D \right)} \right|$ 时循环:

(5)令α为P中重要度最高的属性, 将α放入约简属性集R中, 即 $\scriptstyle R = R \cup \left\{ a \right\}$ ;

(6)当R不满足定义2时, 对 $\scriptstyle \forall a \in R$ , $\scriptstyle B = R$ , 若 $\scriptstyle |{{POS}}_{B - \left\{ a \right\}}^\alpha \left( D \right)\left| \ge \right|{{POS}}_B^\alpha \left( D \right)|$ 时, $\scriptstyle R = R - \left\{ a \right\}$ ;

(7)输出约简集R.

2.3.2 规则提取

输入: 属性约简后的菜谱决策表 $\scriptstyle S = \left( {U,C \cup D,f} \right)$ , θ

输出: 三度覆盖矩阵 $\scriptstyle{{{M}}_{S3}}\left( {PT} \right)$

(1)对 $\scriptstyle\forall {x_i},{x_j} \in S\left( {i \ne {{j}}} \right)$ ;

(2)选定x_i中一条属性 $\scriptstyle{c_k} \in {C_k}\left( {k = 1,2,3, \cdots ,m} \right)$ , 计算缺省值 $\scriptstyle T_{{a_i}}^S$ , 重复

① 判定 $\scriptstyle T_{{a_i}}^S$ 和其他记录x_i的缺省值 $\scriptstyle T_{{a_j}}^S$ 关系;

② 根据式(5)、(6)对决策表当前条件属性值重定义, 得待定矩阵 $\scriptstyle{{M}}\left( {PT} \right)$ ;

(3)对 $\scriptstyle \forall {x_i} \in {{M}}\left( {PT} \right)$

根据式(7), 对 $\scriptstyle{{M}}\left( {PT} \right)$ 的活跃值b_ij重定义;

(4)得到一度覆盖矩阵 $\scriptstyle{{{M}}_{S1}}\left( {PT} \right)$ ;

(5)对 $\scriptstyle\forall {x_i},{x_j} \in {{{M}}_{S1}}\left( {PT} \right)$

if x_i==*

删掉x_i所在记录

else if $\scriptstyle{x_i} = = {x_j}$

记录 $\scriptstyle{\omega _{{x_i}}} = {\omega _{{x_i}}} + {\omega _{{x_j}}}$ , 并删掉x_j;

(6)得到二度覆盖矩阵 $\scriptstyle{{{M}}_{S2}}\left( {PT} \right)$ ;

(7)对 $\scriptstyle\forall {x_i},{x_j} \in {{{M}}_{S2}}\left( {PT} \right)$

if $\scriptstyle{c_i} = {c_j}\& \& {d_i} \ne {d_j}\& \& \theta \left( {{x_i},{x_j}} \right) > \theta $

删减覆盖范围较小的菜谱项;

(8)剩下的菜谱规则构成三度覆盖矩阵 $\scriptstyle{{{M}}_{S3}}\left( {PT} \right)$ ;

(9) 输出三度覆盖矩阵 $\scriptstyle{{{M}}_{S3}}\left( {PT} \right)$ .

3 实验应用

中医营养学目前还没有专门的算法分析, 而中医医药学有很多研究方法^[12]: 专家系统、关联规则、神经网络、遗传算法、粗糙集、决策树, 如文献[13]等将关联规则应用于中医肝病处方用药分析, 文献[2]提出基于加权变精度容差粗糙集模型对中医处方的研究. 西医营养学现存一些探究方法, 文献[11,14,15]提出了Apriori算法、BP神经网络对营养元素的数据挖掘.

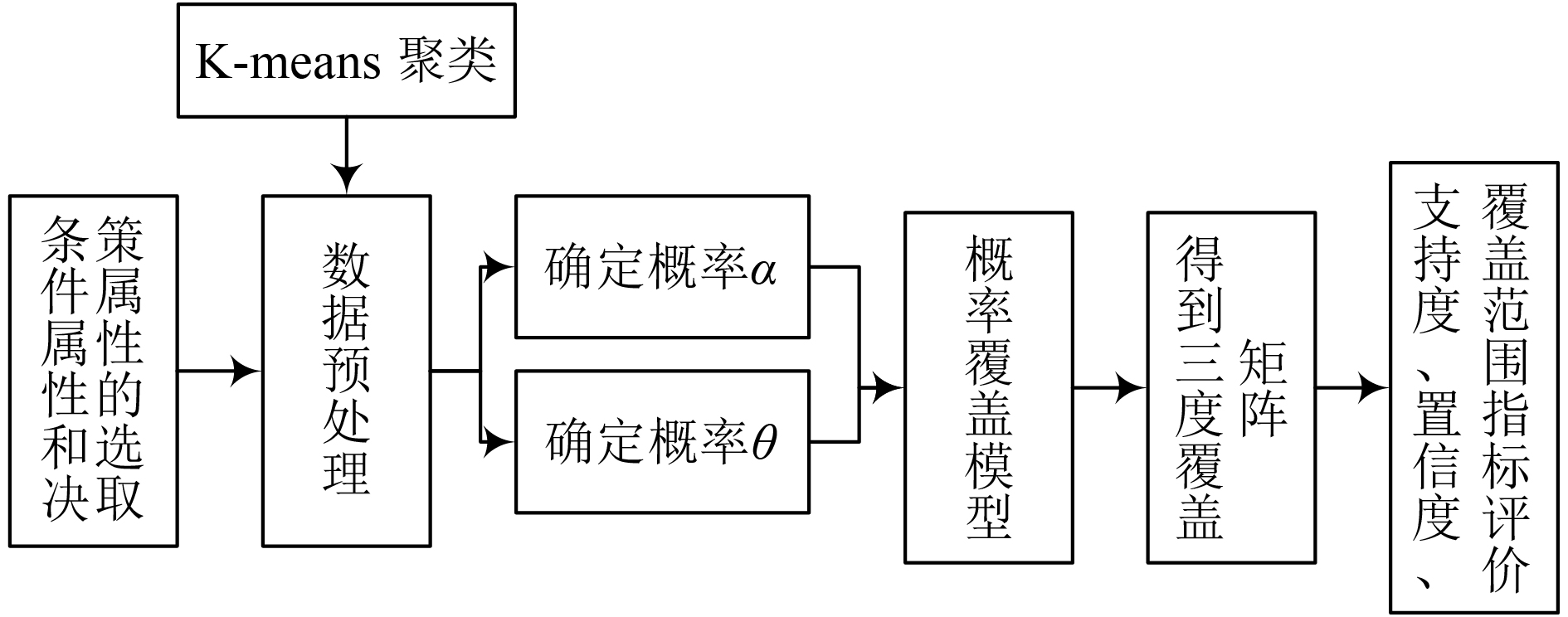
将本文的算法和模型应用到中医营养学菜谱分析, 以食物“四气五味”为切入口, 应用概率覆盖模型, 挖掘出对养肠胃好的决策规则, 从中医营养学的角度对养肠胃的人群提供指导性建议. 具体应用流程设计如图2所示.

3.1 条件属性和决策属性的选取

食物性能与药物性能一致, 包括性味归经、升浮沉降、补泻等^[16], 而中医营养学的研究侧重食物“四气”对人体的调和作用, 所谓“四气”, 即寒、热、温、凉四种性质, 另有不寒不热、不温不凉的饮食, 属于平性. 食物的温热寒凉平属性记载来源于《本草图经》、《植物名实图考》、《中国药植志》、《本草纲目》、《古今医鉴》等经典古书籍对食物类别的区分记载, 整理如表1所示, 另收集《钱家鸣教你养肠胃就该这样吃》^[17]中菜谱食材及其重量, 对一条菜谱有原料 ${y_i}(i = 1,2,3,\cdots )$ , 其原料对应的重量m_i, 所选每一种主要材料的含量均大于10 g, 即以10 g为最小计量单位, 根据公式: $\mathop \sum \limits_1^i \frac{{{m_j}}}{{10}}$ 计算菜谱的温热寒凉平五个属性值, 如表2部分所示. 对于预防一种类型的疾病来说, 这几种属性具有某种程度的紧密联系的特性, 在数据分析上具有可挖掘的意义.

3.2 数据预处理

本文研究目的是识别四气五味的菜谱对肠胃疾病的功能作用, 把属性值极其相似的归并成一类, 在一定程度上保留离散类的分布特征, 探究其属性等级对肠胃疾病的影响力, 因此使用K-means聚类算法^[18]对决策信息表进行数据离散化, K-means聚类含义表如表3.

经过K-means离散化处理后的菜谱决策表如表4所示, ${x_1},{x_2}, \cdots ,{x_n}$ 表示每条菜谱标号, 本文选取菜谱原料的寒、热、温、凉、平五种中医属性为研究对象, 称为条件属性集合C={a, b, c, d, e}, 菜谱是否具有养肠胃功能作为决策属性D={1, 0}.

3.3 参数选取 3.3.1 确定概率取值

α=1根据定义2, 其中正域为以一定的概率(大于阈值)正确分类的属性对象集, 本节探求在何值时, 属性对决策的分类正确率最好. α取值[0, 1](取值间隔为0.1), 时, 为经典粗糙集模型, 以公式(1)计算每个属性的α-正域集合, 并由公式(3)计算当前阈值下5个属性的重要度排序趋势如图3所示.

随着α的减小, 各属性重要度增加直至顶峰, 虽然分类精度允许一定程度的误差, 可以提高含误差的属性对决策的正确率, 但不能一味降低α值, 否则, 会使得各个属性都重要度全部提高, 失去属性约简的意义, 因此α为0.1~0.6时失去分类意义. 当设置α取值接近1时, 分类精度几乎不允许误差, 导致经典粗糙集出现的缺乏容错能力缺陷, 从而舍弃α为0.9、1的取值.

经专家经验: e属性代表菜谱的平性特征, 不论何种菜谱都具备广泛的平值属性, 因此平性不具备评价菜谱特性的标准, 选用平性重要度最小时的α作为概率覆盖模型的概率取值, 因此最优的温热寒凉趋势为α=0.8, 得重要度排序如表5所示.

3.3.2 确定错误覆盖率取值

分析属性值在决策表中出现的规律, 寻找对决策属性影响力最大的属性值, 约简冗余属性值, 舍弃冲突规则. 由公式(8)可知错误覆盖率描述一对冲突矛盾规则覆盖范围的差距性, 如果一条规则的覆盖范围达不到另一条矛盾规则的半数以上, 差距过小, 不能判定其中的矛盾为误差所致, 因此设置错误覆盖率的取值范围为[0.5, 1], 取值间隔为0.1, 控制错误覆盖率θ, 描绘约简力度与错误覆盖率的关系, 如图4所示.

为了提取高质量的知识规则, 由图4所示设置概率覆盖模型的错误覆盖率为0.5, 此时所得模型具备最优性能.

3.3.2 建立概率覆盖模型进行规则提取

由3.3.1节可确定0.8-正域约简集合R={a, b, c, d}, 精简后的菜谱决策表如表6所示.

使用属性约简后的决策表进行值约简, 代入概率覆盖模型得二度覆盖矩阵有20条规则, 如表7所示, 其中含有7对矛盾规则: 3和11、4和13、5和12、8和16、10和19、14和17、15和18, 矛盾规则占比35%, 矛盾规则覆盖样例33%, 矛盾规则现象较为突出, 如果完全舍弃矛盾项, 则所得规则少, 甚至有可能造成知识断层, 因此在分析菜谱营养成分数据时, 需要对矛盾规则进行评估和精简.

设置膳食属性错误覆盖率阈值为0.5, 按照决策表值约简的算法步骤, 低于错误覆盖率阈值的矛盾规则中的较小项判定为误差, 经公式(8)计算, 删减其中5对错误覆盖率率低于0.5的较小矛盾规则: 10、11、12、15、16, 约简后得15条规则的三度覆盖矩阵, 如表8所示.

三度覆盖矩阵决策表是相对比较精准的决策表, 由表8中分析可知, 仍存在两对错误覆盖率难以取舍的矛盾规则4和13、14和17, 比较规则4和13支持度和置信度, 0.0125>0.0063, 0.0183<0.0196, 规则4的支持度远高于规则13, 二者的置信度相差不大, 因此舍弃规则13. 规则14的置信度和支持度均大于规则17, 删减规则17.

经过概率覆盖模型及评价指标分析后, 终得到13条决策规则. 规则1、2、3、8、9相对其他规则而言具有较高的支持度, 在样本数据中也具有较高的覆盖范围, 具有较高的可信性. 规则1、2、3, 7、18、19、20显示寒凉性低、温性高且微热的菜谱有利于养肠胃, 可以暖胃健脾, 促进血液循环, 益气补血, 安神抗寒, 如羊肉萝卜粥、生姜羊肉粥、土豆炖牛肉等, 都属于温补的膳食^[19]. 由规则4、8、14所得, 寒性高的食物会刺激肠胃, 胃肠膜黏硬, 造成肠胃负担, 不利于肠胃吸收. 规则9显示过热的食物损害肠胃, 回归菜谱样例分析, 豆沙炸糕、炸大扁丸子等菜谱不利于肠胃消化吸收. 所得规则揭示了中医寒热调和的原理, 所以, 养肠胃人群要远离大寒过热的食物, 食用菜谱时也要选择少寒多温稍热的菜谱进行调节^[20].

3.4 实验总结

对得到规则质量的评价指标有: 矛盾规则对数, 提取规则条目, 非矛盾规则的覆盖率. 对比本文提出的概率覆盖模型、传统的基于粗糙集的值约简算法和文献[2]针对中医方剂提出的基于加权变精度容差粗糙集模型. 本文构建的概率覆盖模型提取得到较为精简的规则数, 规则中具备较少的矛盾冲突, 非矛盾规则的覆盖率较高, 如图5所示.

另抽取50条除标签菜谱样例为测试数据, 以文中相同的处理方法进行数据处理, 应用本文所得概率覆盖模型, 给菜谱样例标记决策属性, 对比原标签, 有41条标记正确, 正确率达82%, 可以给养肠胃人群饮食给予指导.

4 结束语

本文基于决策粗糙集α-正域约简算法, 利用中医经验确定属性重要度的α概率, 构建待定矩阵, 一度、二度、三度覆盖矩阵提取决策规则, 引入错误覆盖率对值约简规则提取进行了改进, 所得规则与中医医学知识相吻合. 实验结果表明, 该模型提取的矛盾规则数量相对较少, 得出的中医营养规则具有可信度, 对菜谱是否养肠胃具有辨识度, 可用于中医营养学饮食指导. 本文模型还可以应用到政府信访系统、师生教学评价、植物生长监测等领域, 根据不同应用背景控制模型参数, 研究矛盾规则的取舍问题.