目前, 越来越多的用户使用社交网络传播信息, 如微信、新浪微博等. 社交网络中, 信息传播是一个复杂的过程, 不仅受到信息记忆效应[1]、社会加强效应[2,3]、兴趣衰减效应[4]等社会因素影响, 同时还受到用户间亲密度[5]、知识背景[6]、遗忘机制[7]等个体因素影响. 社交网络中复杂的因素影响着用户行为, 考虑不同的传播影响因素, 建立一个符合实际情况的信息传播模型, 对于理解信息传播过程非常重要.
现有研究中, 信息传播常建立在流行病模型基础上进行分析. 张彦超等人[8]结合复杂网络和流行病动力学理论, 考虑节点度和传播机理的影响, 在SIR模型基础上构造了一个基于在线社交网络的信息传播模型, 结果表明初始传播节点的度越大, 信息越容易在网络中迅速传播. 但是, 该模型只是考虑到网络结构对信息传播的影响, 并没有考虑社交网络中社会因素对信息传播的影响.
文献[2]指出信息传播和流行病传播的主要区别是信息传播具有记忆效应和社会加强效应, 并考虑信息传播的记忆效应和社会强化效应建立信息传播模型, 分别在规则网络、小世界网络和随机网络上模拟了信息传播过程, 研究发现小世界网络具有较好的信息传播能力. 但是, 文献[2]只研究了促进信息传播的影响因素, 却没有考虑抑制信息传播的影响因素.
文献[3]认为, 社会加强效应分为正向和负向, 定义接受概率函数来表示社会加强效应对传播的影响, 在SIR模型的基础上提出了在线社交网络中的谣言传播模型. 文献[4]在社交网络上构建了具有社会加强和兴趣衰减效应的谣言传播模型, 认为社会加强和兴趣衰减效应会同时作用于传播态节点, 传播态节点会受到兴趣衰减效应转换为连接态, 连接态又会受到社会加强效应转换为传播态. 文献[9]考虑个体转发阈值差异, 同时将社会加强效应和兴趣衰减效应引入到谣言传播模型中, 建立了两层网络谣言传播模型. 虽然文献[4]和文献[9]同时考虑了促进信息传播的社会加强效应和抑制信息传播的兴趣衰减效应对信息传播的影响, 但是它们认为兴趣衰减是由于用户接收相同信息次数增多而导致的, 其本质与文献[3]所提出的社会负向加强效应是一致的.
以上的研究均指出社会加强效应的累积性对信息传播有重要影响, 但是社会加强效应的累积性需要用户在一段时间内持续多次接收到相同信息才能体现, 但是实际上社交网络中用户无法在短时间内接触到同样信息.
现有研究表明, 社交网络中大多数用户的活跃时间呈现异质性[10,11]. 用户的时间异质性是指, 网络中用户的活跃时间是不一致的, 有些用户是每天固定时间登录微信、微博等社交媒体查看信息, 而有些用户则是每个星期才会登录一次[12]. 同时, 社交网络中用户关注人数会较多, 所以用户接收的信息量大, 导致用户获取到自己感兴趣的信息概率会减少[12]. 因此, 认为社交网络中用户接收到曾经看过的信息会间隔较长时间.
王筱莉等人[7]则考虑用户传播兴趣会随时间的推移而遗忘减少, 指出传播态会自身失去传播兴趣转化为免疫态, 提出了遗忘率变化的谣言传播模型. 王彦本等人[13]根据Ebbinghaus遗忘规律, 时间越长, 人们对信息保持的记忆量减小, 而遗忘信息的概率增大, 研究了遗忘率为指数函数的谣言传播模型. 所以, 长时间没有接触到相同信息会使用户对此信息的新鲜感会降低, 传播信息的概率也会降低.
本文认为信息传播所受社会加强效应期间, 由于用户长时间内没有接收到相同信息, 这段时间会受到遗忘机制的影响, 并将这种影响考虑到SEIR模型中, 重新定义SEIR模型节点状态转移.
2 信息传播影响因素分析社会加强效应是指, 信息传播过程中用户往往会对信息持怀疑态度, 只接收一次信息就进行传播的概率非常有限, 但是如果邻居用户反复提示, 用户多次接收到相同信息, 则用户相信信息并进行传播的概率会大大增加.
由社会加强效应的发展过程可以看出, 用户需要在一段时间内持续多次接收到相同信息, 社会加强效应才能体现. 但是, 实际中用户往往接收到相同信息的时间间隔较长, 而长时间没有接收到信息, 人们会遗忘信息, 对信息传播概率会随着时间推移而减少. 因此, 本文认为社会加强效应期间会受到遗忘机制的影响.
在信息传播过程中, 社会加强效应期间受到遗忘机制的影响, 使信息的传播概率在社会加强效应影响的基础上减少, 所以将社会加强效应影响后的信息传播的概率作为遗忘机制的初值. 借鉴文献[3]关于社会加强效应的研究, 定义信息传播过程社会加强效应期间由遗忘机制引起的传播概率p为:
| $p = 1 - \left( {1 - \lambda } \right){{{e}}^{ - b \times \left( {m - 1} \right)}} - (1 - {{{e}}^{ - \beta \tau }})$ | (1) |
式中,
若接收到信息的时间间隔τ足够长, 使信息传播所受遗忘机制的影响大于社会加强效应的影响, 即:
| $1 - {{{e}}^{ - \beta \tau }} > 1 - \left( {1 - \lambda } \right){{{e}}^{ - b \times \left( {m - 1} \right)}}$ | (2) |
说明用户连续两次接收信息之间, 由于遗忘信息的速率过快, 用户已经完全遗忘信息, 此时认为用户不可能接收信息转变为传播用户.
对于不考虑社会加强效应期间遗忘机制的影响, 此时用户会连续接收到邻居用户的信息, 接收到信息的时间间隔τ=0, 则信息的传播概率p为:
| $p = 1 - \left( {1 - \lambda } \right){{{e}}^{ - b \times \left( {m - 1} \right)}}$ | (3) |
若接收到信息的时间间隔τ适中, 使信息传播所受遗忘机制的影响小于社会加强效应的影响, 即:
| $1 - {{{e}}^{ - \beta \tau }} < 1 - \left( {1 - \lambda } \right){{{e}}^{ - b \times \left( {m - 1} \right)}}$ | (4) |
则信息的传播概率p可化简为:
| $p = {{{e}}^{ - \beta \tau }} - \left( {1 - \lambda } \right){{{e}}^{ - b \times \left( {m - 1} \right)}}$ | (5) |
在SEIR模型中, 将网络中节点分为4中状态, 分别为: 未知态(S)、潜伏态(E)、传播态(I)、免疫态(R). 未知态是尚未接触到信息, 对信息处于完全未知, 但是有机会接收到信息的状态; 潜伏态是已经获知邻居节点发送的信息, 但是还没有确定信息的真实性没有进行信息传播, 存在一定的概率进行传播; 传播态是相信邻居节点发送的信息, 对进行传播, 并以一定的概率转化为免疫态; 免疫态是已经听过或知道信息, 不会再进行信息传播的状态.
由于未知态没有接触到信息, 即接收信息次数一直处于零, 所以不会受到社会加强效应和遗忘机制的影响; 潜伏态对信息持有怀疑态度, 会多次接收邻居传播态反复传来的信息, 受到社会加强效应的影响, 但是由于接收时间间隔较长, 在没有接收到信息期间, 会遗忘信息受到遗忘机制的影响; 由于传播态已经相信信息并进行传播, 所以传播态不会受到社会加强效应的影响, 但是随着时间的推移, 传播态同样也会遗忘信息受到遗忘机制的影响; 免疫态是传播过程中的终态, 其状态不会改变.
在SEIR模型中, 4类状态节点之间的状态转移不仅依赖于节点自身的状态, 还与邻居节点的状态有关, 其状态转移规则定义如下:
(1) 未知态S只与传播态I接触一次后, 未知态S以初始传播率λ转化为传播态I, 否则以概率p1转化为只接触到信息但并未传播的潜伏态E, p1=1–λ.
(2) 潜伏态E会与传播态I接触多次, 但是由于接触传播态I的时间间隔较长, 在没有接触传播态I期间, 会遗忘信息, 受到遗忘机制的影响, 因此潜伏态E会以概率p转化为传播态I; 对于足够长时间都没有接触到传播态I的潜伏态E, 认为该潜伏态已经遗忘信息, 不会传播信息, 从而转换为免疫态; 同时对于未转化传播态I的潜伏态, 会以概率p2转化为免疫态R, p2=1–p.
(3) 若传播态I的邻居节点存在未知态S或潜伏态E时, 传播态I将信息传播给邻居节点后, 传播态I直接转化为免疫态S; 若传播态I的邻居不存在未知态S或潜伏态E时, 传播态I自身会遗忘信息以概率p3转换为免疫节点,
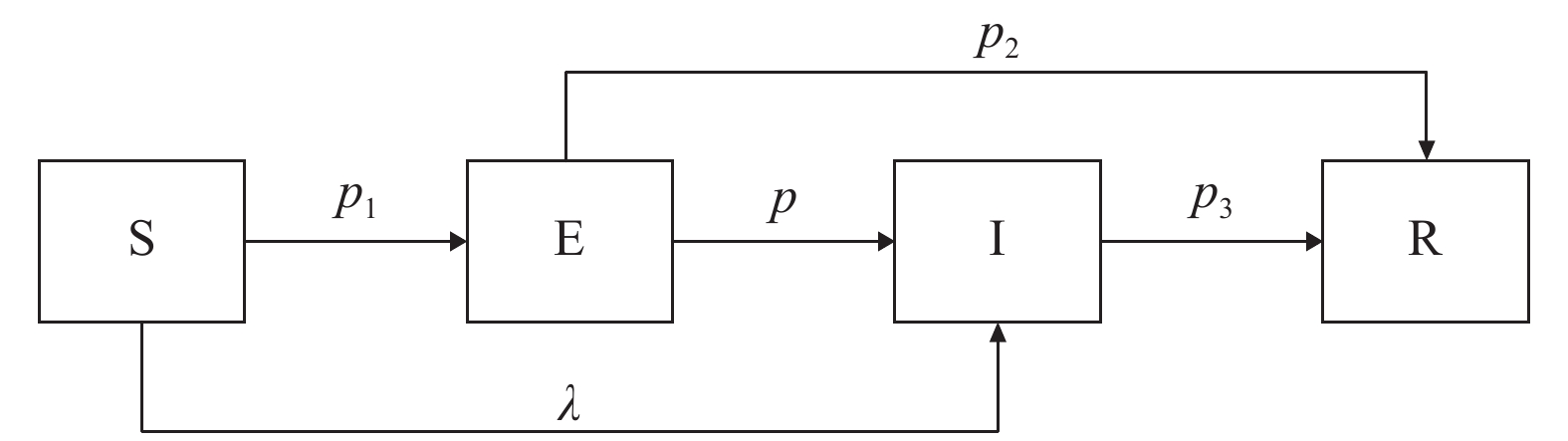
|
图 1 SEIR模型节点状态转移图 |
对于上述模型做以下说明:
(1) 假设节点的生命周期要远大于一条信息传播有效传播时间, 即在信息传播过程中不考虑用户的增加和用户的移出;
(2) 假设节点不会重复传播同一条信息, 即社会加强效应多次接收到的信息均是来自不同邻居用户所传播的;
(3) 假设用户同等看待不同邻居用户传来的信息, 即认为社会加强效应每次接收到的信息对于传播的影响权重是一样的.
4 实验仿真实验数据采用Facebook数据网络(Facebook数据取自http://snap.stanford.edu/data/)进行实验仿真, 运用社会网络分析软件Gephi统计出该网络的基本特征参数如下: 节点总数为4039, 总边数为88 234, 平均度为21.85, 网络直径为17, 平均聚集系数为0.60, 平均路径长度为4.33.
4.1 各种状态节点密度变化社会加强效应期间考虑遗忘机制情况下, 在SEIR模型中, 任意选取网络中一个节点为传播节点, 其余节点为未知节点, 设置初始参数为λ=0.5, b=1, β=1, τ=3, 进行了30次重复传播实验, 并对所得结果取平均值, 得到社会加强效应期间考虑遗忘机制情况下SEIR模型各类节点状态变化趋势如图2所示.
由于社交网络信息传播极快使得未知态S密度在初始传播阶段迅速减少, 最终趋于稳定, 稳定密度约为0.23; 潜伏态E密度逐渐增加, 然后达到一峰值, 峰值密度约为0.05, 然后逐渐减少, 最终减为0, 这是由于初始阶段部分未知态节点接收到信息没有转化为传播态而转化为潜伏态, 使潜伏态节点数量增大, 然后由于足够长时间没有再次接触到信息, 从而遗忘信息转化为免疫态; 传播态I密度在信息传播初期迅速增大呈现一峰值, 峰值密度约为0.13, 之后由于免疫节点抑制信息的扩散作用使得更多节点进入免疫状态, 从而传播节点逐渐减少, 最终减少0; 免疫态R密度在信息传播过程中快速增长最终达到稳定, 稳定密度为0.76.

|
图 2 考虑遗忘机制情况下SEIR模型各类节点状态变化趋势 |
4.2 接收信息的时间间隔对信息传播的影响
传播态密度代表着网络中信息传播的活跃程度, 可以反映出信息在网络中的传播速率. 任意选取网络中一个节点为传播节点, 其余节点为未知节点, 设置初始参数为λ=0.5, b=1, β=1, 分别取τ=1, τ=2, τ=3进行了30次重复传播实验, 对所得结果取平均值, 得到SEIR模型中传播节点密度的变化趋势, 如图3所示.
从图3中可以看出, 传播节点密度的变化趋势大致是相同的, 在信息传播初期快速增加, 然后达到一个峰值, 此时传播态密度是最大的, 之后传播态密度快速减少, 最后减为零. 接收信息的时间间隔对传播态密度峰值影响明显, 当τ=1时, 传播态峰值密度约为0.28, 当τ=2时, 传播态峰值密度约为0.21, 当τ=3时, 传播态峰值密度约为0.13. 接收信息的时间间隔越长, 传播态峰值密度越小, 并且达到峰值所需的时间越少. 因此, 接收信息的时间间隔越长, 信息的传播速率越慢.
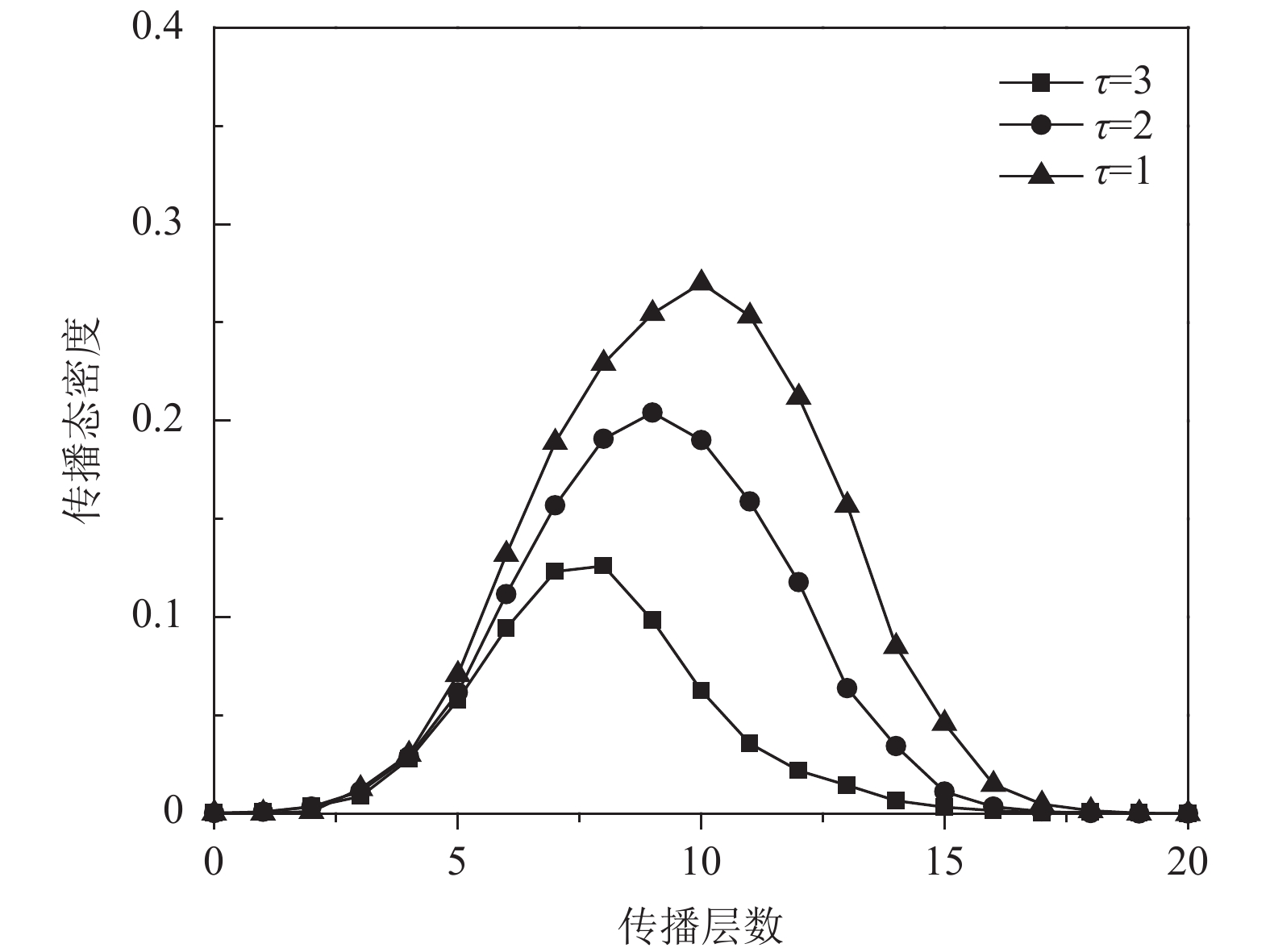
|
图 3 接收信息的时间间隔对传播态密度的影响 |
4.3 社会加强效应期间考虑遗忘机制和不考虑遗忘机制的比较
社会加强效应期间不考虑遗忘机制情况下, 在SEIR模型中, 取参数λ=0.5, b=1, 同样任意选取网络中一个节点为传播节点, 其余节点为未知节点, 进行了30次重复传播实验, 对所得结果取平均值, 得到信息传播社会加强效应期间不考虑遗忘机制情况下SEIR模型各类节点状态变化趋势如图4所示.
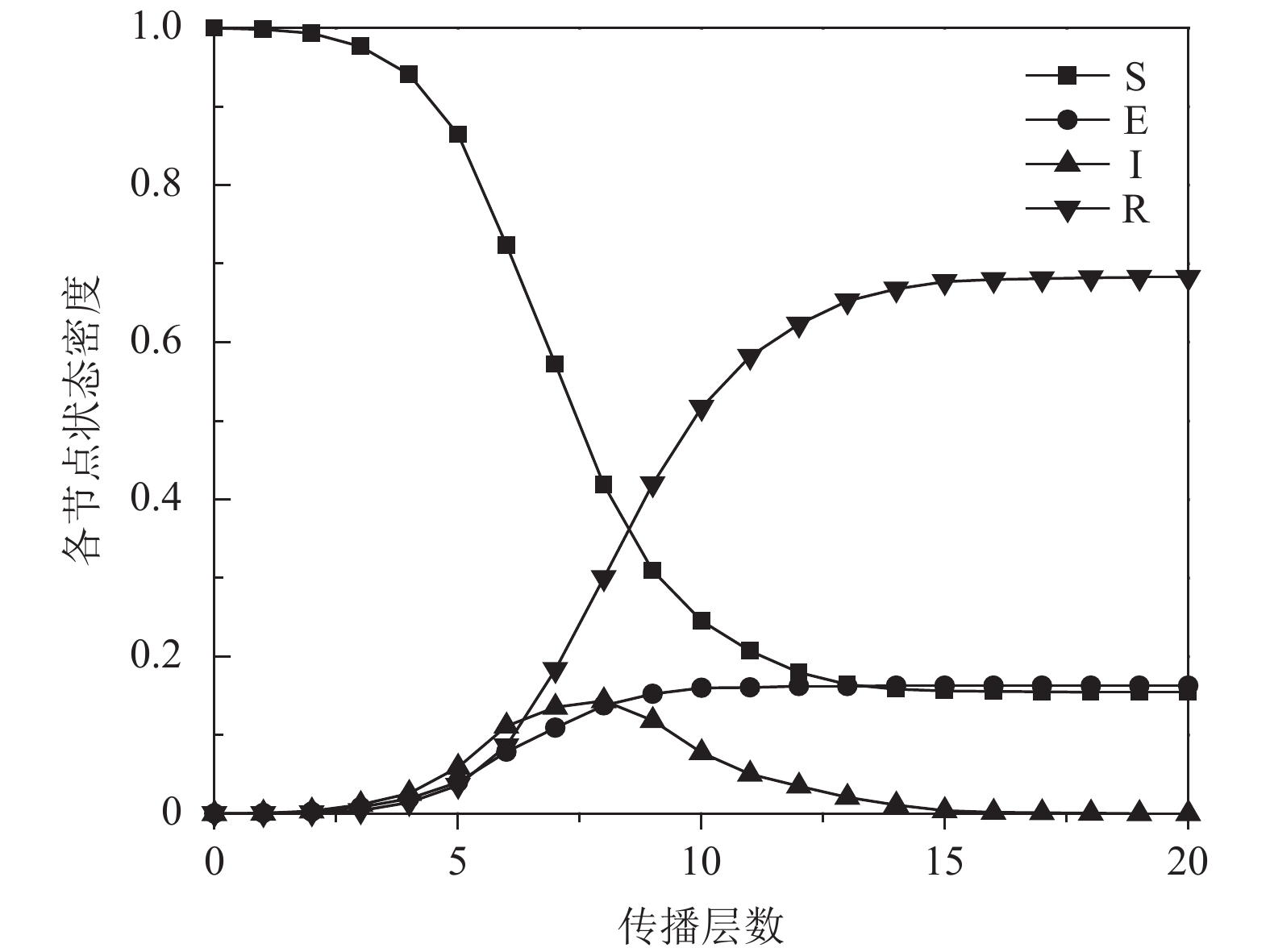
|
图 4 不考虑遗忘机制情况下SEIR模型各类节点状态变化趋势 |
对比图4和图2可以看出, 未知态S、传播态I和免疫态R的密度变化趋势大致是相同的, 对于图4不考虑机制情况下潜伏态E密度会持续增加最后达到稳定不再变化, 而图2考虑遗忘机制情况下潜伏态E密度先不断增加然后达到一峰值后逐渐减为零. 这是由于考虑遗忘机制情况下潜伏态接收相同信息期间存在较长的时间间隔, 受到遗忘机制的影响, 潜伏态用户会遗忘信息, 转换为免疫态, 所以潜伏态密度会有减少的趋势.
潜伏态、传播态和免疫态密度之和代表着网络中知道信息的用户比例, 可以反映出信息在网络中的传播范围. 图2中潜伏态、传播态和免疫态密度稳定时之和约为0.76, 图4中潜伏态、传播态和免疫态密度稳定时之和约为0.88. 所以, 考虑遗忘机制情况下潜伏态、传播态和免疫态密度之和较小, 信息的传播范围较窄.
5 结论分析本文研究了社交网络中信息传播所受社会加强效应影响期间, 由于用户长时间没有接收到信息, 会受到遗忘机制的影响, 并将这种影响考虑到SEIR模型中, 重新定义SEIR模型节点状态转移. 最后通过社交网络数据分析, 接收信息时间间隔对传播态用户影响明显, 接收信息的时间间隔越长, 信息的传播速率越慢; 社会加强效应期间考虑遗忘机制情况下潜伏态、传播态和免疫态密度之和较小, 信息的传播范围较窄.
| [1] |
葛晓艳, 张宁. 记忆效应在信息传播过程中的效用研究. 物流科技, 2015, 38(10): 21-23, 27. DOI:10.3969/j.issn.1002-3100.2015.10.005 |
| [2] |
Lü LY, Chen DB, Zhou T. The small world yields the most effective information spreading. New Journal of Physics, 2011, 13(12): 123005. DOI:10.1088/1367-2630/13/12/123005 |
| [3] |
王辉, 韩江洪, 邓林, 等. 基于移动社交网络的谣言传播动力学研究. 物理学报, 2013, 62(11): 96-107. |
| [4] |
张亚明, 唐朝生, 李伟钢. 在线社交网络谣言传播兴趣衰减与社会强化机制研究. 情报学报, 2015, 34(8): 833-844. |
| [5] |
阚佳倩, 谢家荣, 张海峰. 社会强化效应及连边权重对网络信息传播的影响分析. 电子科技大学学报, 2014, 43(1): 21-25. |
| [6] |
彭慧洁, 朱君璇. 微信网络的信息传播模型研究. 现代情报, 2016, 36(11): 37-42. DOI:10.3969/j.issn.1008-0821.2016.11.007 |
| [7] |
王筱莉, 赵来军, 谢婉林. 无标度网络中遗忘率变化的谣言传播模型研究. 系统工程理论与实践, 2015, 35(2): 458-465. DOI:10.12011/1000-6788(2015)2-458 |
| [8] |
张彦超, 刘云, 张海峰, 等. 基于在线社交网络的信息传播模型. 物理学报, 2011, 60(5): 050501. |
| [9] |
覃志华, 刘咏梅. 考虑转发阈值差异的微信两层网络谣言传播演化研究. 情报杂志, 2016, 35(8): 162-168. |
| [10] |
Zhao ZD, Cai SM, Huang JM, et al. Scaling behavior of online human activity. EPL (Europhysics Letters), 2012, 100(4): 48004-48009. DOI:10.1209/0295-5075/100/48004 |
| [11] |
Radicchi F. Human activity in the web. Physical Review E, 2009, 80(2): 026118. DOI:10.1103/PhysRevE.80.026118 |
| [12] |
李旭军, 刘业政, 荆科, 等. 节点的时间异质性对信息传播的影响. 系统科学与数学, 2016, 36(10): 1630-1642. |
| [13] |
王彦本, 蔡皖东. 社交网络中考虑遗忘机制的谣言传播. 西北工业大学学报, 2016, 34(2): 349-355. |
 2018, Vol. 27
2018, Vol. 27



