2. 武夷学院 认知计算与智能信息处理福建省高校重点实验室, 武夷山 354300;
3. 华东师范大学 上海可信研究重点实验室, 上海 200062
The Key Laboratory of Cognitive Computing and Intelligent Information Processing of Fujian Education Institutions, Wuyi University, Wuyishan 354300, China;
Shanghai Key Laboratory of Trustworthy Computing, East China Normal University, Shanghai 200062, China
超宽带(Ultra Wide-Band, UWB)脉冲无线电(Impulse Response, IR)系统引起了学术界和行业的兴趣. UWB-IR实现的主要挑战之一是信道估计[1]. 压缩感知(Compressive Sensing, CS)[2,3]可以应用于UWB信道估计, 以克服常规最大似然(Maximum Likelihood, ML)信道估计器的高速率采样问题[4]. 在文献[5]中, 采用贝叶斯压缩感知, 提出了两种有效的算法, 以减少主动传感器节点的数量, 同时保持高性能. 在文献[6]中, 采用基于贝叶斯压缩感知(Bayesian Compressive Sensing, BCS)的策略来解决入射到天线阵列上的电磁窄带信号(Direction of Arrivals, DoAs)估计问题. 在文献[7]中, 主要贡献是利用噪声方差学习在性能改进和适用性增强方面的能力. 在文献[8]中, 压缩感测技术应用于数据恢复, 模拟通信系统期间对采样率降低进行了分析. 文献[9]提出无线网络通信的实现方法以及对无线各模块具体的实现过程进行探讨.
在文献[10,11]中, BCS框架已被应用于各种UWB信道模式和噪声条件下的信道估计. 多任务CS(Muti-Task Compressive Sensing, MTCS)[12]应用于UWB信道估计中的多个任务. MTCS和隐马尔可夫模型(HiddenMarkov Model, HMM)层次Dirichlet过程(Hierarchy Dirichle Processing, HDP)多任务CS(HDP-HMM-MTCS)具有共享相似机制, 可以利用共享机制执行多任务压缩感知信号. 然而, 主要区别在于MTCS使用伽马-高斯先验, 而HDP-HMM-MTCS使用层次Dirichlet过程HDP. 在本文中, HDP-HMM-MTCS用于解决多个集群之间的数据共享问题, 用于UWB通信中的信道估计和降低计算复杂度. 本文的贡献如下:
(1) 提出了一种新颖的CS框架, 表示为HDP-HMM-MTCS, 用于UWB信道估计. HDP-HMM-MTCS的优点是利用隐马尔可夫模型采用树形结构来解决多个任务中的数据共享问题, 采用HDP [8]以前的方法, 减少了数据传输过程中的数据丢失; 而MTCS算法可以使用伽马-高斯先验在多个群集之间共享数据.
(2) 对于CS测量, 比较HDP-HMM-MTCS和MTCS [12], 单任务CS (Simple-Task Compressive Sensing, STCS)[12], 正交匹配追踪(Orthogonal Matching Pursuit, OMP)[10], L1 magic[1]和新的算法如改进的BCS算法[13], 多经字典自适应算法BCS[14]和特征字典自适应算法BCS[14]的信道估计性能, K=200, 相对于CS比率(CSR)和信噪比(SNR)值. 图3和图4分别显示视距(LOS)和非视距(NLOS)环境几种算法比较情况. 仿真结果表明, HDP-HMM-MTCS的信道估计性能(如均方误差(Mean Square Error, MSE), 误码率(Bit Error Ratio, BER), 归一化均方误差(Normalized Mean Square Error, NMSE)和峰值SNR(Peak Signal Noise Ratio, PSNR))优于那些MTCS和其他算法. 此外, 从表1可以看出, HDP-HMM-MTCS的计算时间小于MTCS和其他算法的计算时间.
降低信号传输误差和信号数据共享是UWB信道估计的挑战之一. MTCS算法[11] 采用高斯先验方法的共享机制执行多任务压缩感知信号. 本文采用HDP-HMM-MTCS算法即采用隐马尔可夫模型层次Dirichlet过程解决多信号集群之间的共享问题. 同时, 算法仿真结果显示虽然HDP-HMM-MTCS算法的计算复杂度和MTCS算法的计算复杂度相等, HDP-HMM-MTCS算法的时间复杂度却要低于MTCS算法的时间复杂度, 同时和最新算法比较时间复杂度, 仿真结果同样显示HDP-HMM-MTCS算法的时间复杂度要比最新算法复杂度低.
本文的其余部分安排如下. 在第1节中, 建立了HDP-MTCS框架. 在第2节中, 描述了HDP-HMM-MTCS基本框架, 并提供了在UWB系统中用于信道估计的详细HDP-HMM-MTCS框架. 在第3节中, 介绍和讨论了仿真结果, 并在第4节中得出结论.
1 HDP-MTCS框架应用于UWB信道估计在本节中, 我们提出了一个离散时间等效的UWB信道模型. 在任何信号的稀疏域(时域, 频域等)中, 随机较小的测量降低采样率.
1.1 UWB的MTCS框架首先, 为了实现离散时间信道模型, 将通用连续时间信道脉冲响应(CIR) h(t):
| $h(t) = \mathop \sum \limits_{m = 1}^M {h_m}\xi (t - {\gamma _m})$ | (1) |
其中
| $h(t) = \mathop \sum \limits_{p = 1}^P {\omega _p}\xi (t - p\Delta T)$ | (2) |
其中, P为信道离散时间间隔数.
| $h = {[{\omega _{1,}}{\omega _2},\cdots,{\omega _P}]^{\rm T}}$ | (3) |
考虑到h具有K个非零系数, 假定测量值K<<P, 则信道的稀疏假设是有效的.
假设由K个测量值接受信号表示为
| ${\vec g_i} = \mathop \sum \limits_{j = 1}^K {\vec E_j}{h_j} + {\vec \eta _j}$ | (4) |
其中, 标量矩阵
| $\begin{array}{*{20}{l}}{{{\tilde g}_i} = \mathop \sum \limits_{j = 1}^K {\Theta _j}{{\tilde E}_j}{h_j} + {\Theta _j}{{\tilde \eta }_j}}\\\quad { = \mathop \sum \limits_{j = 1}^K {\Theta _j}{{\tilde H}_j} + {{\tilde \rho }_j}}\end{array}$ | (5) |
白噪声(Additive White Gaussian Noise, AWGN)
| ${\vec H_i} = \max \left\| {\vec H_i} \right\|_1\text{且}\left\| \Theta {\vec H_i} - {\vec g_i} \right\| \ge \varsigma $ | (6) |
| ${\vec g_i} = \mathop \sum \limits_{j = 1}^K {\Theta _j}{\tilde {\vec H}} + {\vec \rho _j}$ | (7) |
| $p({\tilde {\vec g}_i}|{\vec {\tilde H}_i},{\vec \beta _0}) = 2\pi \vec \beta _0^{ - {K_{1/2}}}\exp \left\{ {\frac{{{\beta _0}}}{2}\left\| {{\theta _i}{{\vec H}_i} - {{\mathop g \limits^ \rightharpoonup}_i}} \right\|_2^2} \right\}$ | (8) |
在可压缩条件下, 信道估计问题变为线性回归. 对于关于上述超先验的MTCS模型[7], 参数β是Gamma-Gaussian先验参数和数据共享多个群集, 服从
为了解决分组数据共享问题, HDP在先前的分布中被应用于分组数据因子[12]. 假设CS测量对于接受信号 
| $\begin{array}{*{20}{l}}{{{\vec {\tilde g}}_0}|\beta ,{{\tilde g}_0}\sim DP({{\tilde \beta }_0},{{\tilde g}_0})}\\{{\varpi _{ij}}|{{\vec {\tilde g}}_i}\sim{{\vec g}_i}}\\{{S_{ij}}|{\varpi _{ij}}\sim F({\varpi _{ij}})}\end{array}$ | (9) |
其中,

| ${{\vec {\tilde g}}_i} = \mathop \sum \limits_{i = 1}^\infty {\chi _{11}}{\xi _q}$ | (10) |
基于公式(9), 每子模型对应不同组, χ是混合权重

|
图 1 四组HDP混合模型的图形表示 |
1.3 UWB系统的HDP-MTCS信道估计算法
为了便于后验计算, 采用指标变量
HDP-MTCS模式表示为:
| $\begin{array}{*{20}{l}}{{{\vec {\tilde g}}_i}|{h_i},{\xi _0}\sim DP(\vec E{h_i},\xi _0^{ - 1})}\\{{h_{ij}}|{l_{j,}}\left\{ {{\xi _i}} \right\}_{i-1},P\sim DP(0,\xi _{i - 1}^{ - 1})}\\{{l_j}|\left\{ {{\alpha _q}} \right\}\sim Multinomial\left( {{{\left\{ {{\alpha _q}} \right\}}_{k - 1, \cdots P}}} \right)}\\{{\alpha _q}\sim Beta(1,{\xi _0})}\\{{\xi _i}|e,f\sim\mathop \prod \limits_{j = 1}^m Ga(e,f)}\\{{\xi _0}{\rm{\sim}}Ga(c,d)}\end{array}$ | (11) |
其中
| $P({\vec {\tilde h}_i}|{\kern 1pt} e,f){\kern 1pt} = \mathop \prod\nolimits_{j = 1}^K DP({h_{i,j}}{\kern 1pt} |{\kern 1pt} {\kern 1pt} 0,\xi _q^{ - 1})Ga({\xi _q}{\kern 1pt} |{\kern 1pt} {\kern 1pt} e,f)d{\xi _q}$ | (12) |
| $P(Q\left\| {U,V} \right. ) = \frac{{P(U\left| {Q)P(Q} \right|V)}}{{\mathop \smallint P(U\left| {Q)P(Q} \right|V)dQ}}$ | (13) |
其中,
| $Q = \left\{ {{\beta _0},{\alpha _i},{{\left\{ {{{\tilde h}_i}} \right\}}_{i = 1, \cdots ,M}},{{\left\{ {{\ell _j}} \right\}}_{i = 1, \cdots ,M}},{{\left\{ {{\xi _i}} \right\}}_{i = 1, \cdots ,M}}} \right\}$ |
表示信道估计测量参数矩阵集合.
| $\log P(U{\kern 1pt} | V) = \Gamma (\lambda (Q))+ {\Psi _{KL}}(\lambda (Q) \left\| \right. \rho (Q | U,V))$ | (14) |
其中,
| $\Gamma (\lambda (Q)) = \mathop \smallint \lambda (Q)\log \frac{{P(U\left| {Q)P(Q} \right|V)}}{{\lambda (Q)}}dQ$ | (15) |
同时,
| $\lambda (Q) = \lambda ({\xi _0})\lambda (\xi )\lambda (\alpha )\mathop \prod \nolimits_{j = 1}^K \lambda ({\ell _j})\mathop \prod \nolimits_{j = 1}^K \lambda ({g_j})\mathop \prod \nolimits_{q = 1}^K \lambda ({\xi _q})$ | (16) |
根据文献[11], 式(15)中,
| $\begin{array}{*{20}{l}}{\lambda ({\xi _0})\sim Ga(c,d)}\\{\lambda (\xi )\sim Ga(e,f)}\\{\lambda ({\ell _j})\sim Multino\min al({{\left\{ {{\alpha _q}} \right\}}_{k = 1, \cdots ,N}})}\\{\lambda ({\vec {\tilde g}})\sim DP(\Theta {{\vec {\tilde H}}_i}\xi _{0.1}^{ - 1})}\\{\lambda ({\xi _q})\sim \mathop \prod \limits_{j - 1}^m Ga({\xi _q}|{c_{q,j}}{d_{q,j}})}\end{array}$ |
HDP应用开发多任务压缩感知MTCS信号空间的隐马尔可夫模型. HMM模型涉及系列混合模型, 其中涉及到当前状态的每个值. 当前状态
|
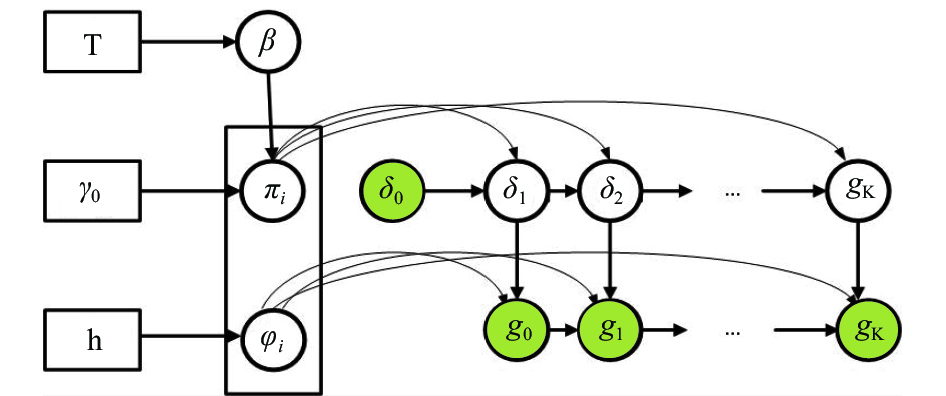
图 2 分层Dirichle隐马尔科夫模型过程模型(HDP-HMM-MTCS) |
因此, 通过经典HMM的HDP混合模型替换传统的有限混合模型集来定义非参数变量HMM, 就是HDP-HMM. 利用棍棒公式描述HDP-HMM模型(如图2):
| $\begin{array}{*{20}{l}}{\beta {\rm{|}}T\sim GEM(T)}\\{\pi {\rm{|}}{\gamma _0},\beta \sim DP({\gamma _0},\beta )}\\{{\varphi _k}|H,h\sim H(h)}\\{{\delta _t}|\left\{ \pi \right\}_{j = 1}^\infty ,{\delta _{t - 1}}\sim {\pi _{{\chi _{t - 1}}}}}\\{{g_t}|\left\{ \varphi \right\}_{j = 1}^\infty ,{\delta _t}\sim f({\varphi _{{\chi _t}}})} \end{array}$ | (17) |
其中, 可变序列
| $\begin{array}{*{20}{l}}{{\delta _k}|{\delta _{k - 1}}({\pi _i})_{i = 1}^\infty \sim {\pi _{{\delta _{k - 1}}}}}\\{{g_k}|{\delta _k},({\varphi _i})_{i - 1}^\infty \sim G({\varphi _{{\delta _k}}})}\end{array}$ | (18) |
采用棍棒模型描述
| ${\vec g_0} = \mathop \sum \limits_{q = 1}^\infty {\alpha _q}{\xi _q}$ |
同时,
| ${\xi _q} \sim {\vec g_0},\alpha \sim Beta(1,\varepsilon ),{\alpha _q} = \alpha _q^{\prime}\prod\limits_{i = 1}^\infty {{\chi _{i1}}} {\xi _i}$ |
假设
下一节, 我们研究了CS比率, 表示为CSR, 定义为K/P, SNR区域和IEEE 802.15.4a信道模型对HDP-HMM-MTCS信道估计性能的影响, 并将结果与STCS[12], MTCS [12], OMP[10]和l1 magic[1]比较.
3 仿真结果假设CS测量的性能K=200, 我们评估估计信道向量的NMSE和PSNR性能, 通道系数为

图3(a)和(b)绘制了重建NMSE和PSNR与UWB通信的CSR; 可以看出, 在稀疏信道与CSR中, HDP-HMM-MTCS框架的NMSE和PSNR性能优于MTCS和其他算法的NMSE和PSNR性能. 因此, (1)提出的HDP-HMM-MTCS框架达到最佳效果, (2)具有树结构的模型(HDP-HMM-MTCS)优于没有结构的模型. 这可能是因为HDP-HMM-MTCS算法可以使用先前的HDP从群集中的“K”任务共享所有CS数据, 而MTCS算法仅使用Gamma-Gaussian先验共享数据. 因此, HDP-HMM-MTCS算法提高了NMSE和PSNR性能, 超越了MTCS和其他算法的性能.
图4分别描述了LOS和NLOS情况下的MSE和BER曲线. 图4(a)和(c)分别描述了LOS和NLOS环境下的BER性能曲线; 比较确定了HDP-HMM-MTCS算法的BER性能优于MTCS和其他算法, 不管LOS和NLOS环境如何. 图4(b)和(d)分别显示LOS和NLOS环境下的MSE性能曲线, 确定与MTCS和其他算法相比, HDP-HMM-MTCS具有最低的MSE, 因为HDP-HMM-MTCS解决了数据共享问题在使用HDP先验的K任务中, MTCS使用Gamma-Gaussian先验解决问题, 而另一种算法无法解决数据共享问题. 因此, HDP-HMM-MTCS可以是稀疏信道模式的有效信道估计方法.

|
图 3 比较STCS (CS measure k=200), MTCS, HDP-MTCS, OMP, and the L1 MAGIC算法的MSE和PSNR性能 |

|
图 4 比较LOS和NLOS情况下的MSE和BER性能 |
最后, 在表1中, 提出了HDP-HMM-MTCS, MTCS-MTCS, STCS, OMP, l1 magic以及最新的算法如改进的贝叶斯压缩感知(BCS)算法[13], 多经字典自适应算法BCS[14]和特征字典自适应算法BCS[14]的计算时间; 其主要信道模型适用于IEEE 802.15.4a信道估计. 模拟在具有2.4 GHz, Intel Core i34000M CPU和12 GB RAM的计算机上实现. 在LOS环境下, 我们假设传输的参数时间为5 s, T=200 ns, 采用2-PPM调制方案. 在表1中, 作为STCS, OMP和l1 magic只处理简单的CS任务, 对于四个CS任务(K=200, 300, 400和500), STCS的计算时间{1.3711 s, 3.0223 s, 5.2044 s}分别低于其他两种算法. 然而, MTCS和HDP-HMM-MTCS算法可以同步4项任务(K=200, 300, 400和500)的实现, 仿真结果表明, HDP-HMM-MTCS(1.92145 s)的计算时间明显小于MTCS, {6.4797 s}和其他算法. 从仿真结果可以看出, HDP-HMM-MTCS算法比MTCS和其他算法更有效.
| 表 1 K不同测量数据时STCS, MTCS, HDP-MTCS, OMP和L1 MAGIC的执行时间比较 |
5 结论
在本文中, 我们研究了HDP-HMM-MTCS在LOS和NLOS环境下的UWB通信的信道估计性能. 使用标准化IEEE 802.15.4a信道模式的稀疏结构, 我们研究HDP-HMM-MTCS信道估计性能, 并将其与MTCS, STCS, OMP, l1 magic以及最新的估计结果进行比较. 仿真结果表明, 由于HDP-HMM-MTCS采用树形结构解决了多个任务间的数据共享问题, 所以在信道估计中使用HDP, 在LOS和NLOS下, 优于MTCS和其他具有稀疏信道结构的算法环境;因此, 它是一种有效的信道估计方法. 此外HDP-HMM-MTCS的计算时间在MTCS和其他算法中是最小的, 其计算复杂度为O(PK2), 其比常规ML解决方案更有效. 本文研究的UWB通信中的HDP-HMM-MTCS应用只是一个开始; HDP-HMM-MTCS将来会在其他各个领域得到应用.
| [1] |
Cheng XT, Wang MY, Guan YL. Ultrawideband channel estimation: A Bayesian compressive sensing strategy based on statistical sparsity. IEEE Transactions on Vehicular Technology, 2015, 64(5): 1819-1832. DOI:10.1109/TVT.2014.2340894 |
| [2] |
Donoho DL. Compressed sensing. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [3] |
Candes EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [4] |
Paredes J, Arce GR, Wang ZM. Ultra-wideband compressed sensing: Channel estimation. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(3): 383-395. DOI:10.1109/JSTSP.2007.906657 |
| [5] |
Ji SH, Xue Y, Carin L. Bayesian compressive sensing. IEEE Transactions on Signal Processing, 2008, 56(6): 2346-2356. DOI:10.1109/TSP.2007.914345 |
| [6] |
Özgör M, Erkucuk S, Cirpan HA. Bayesian compressive sensing for ultra-wideband channel models. Proceedings of the 35th International Conference on Telecommunications and Signal Processing (TSP). Prague, Czech Republic. 2012. 320–324.
|
| [7] |
Ji SH, Dunson D, Carin L. Multitask compressive sensing. IEEE Transactions on Signal Processing, 2009, 57(1): 92-106. DOI:10.1109/TSP.2008.2005866 |
| [8] |
Teh YW, Jordan MI, Beal MJ, et al. Hierarchical dirichlet processes. Journal of the American Statistical Association, 2006, 101(476): 1566-1581. DOI:10.1198/016214506000000302 |
| [9] |
邢彦廷, 吕立, 廉东本. 视频会议中的网络通信控制系统. 计算机系统应用, 2015, 24(4): 249-252. |
| [10] |
Jhang JW, Huang WH. A high-SNR projection-based atom selection OMP processor for compressive sensing. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2016, 24(12): 3477-3488. DOI:10.1109/TVLSI.2016.2554401 |
| [11] |
Cadavid AN, Ramos M. Simulation and analysis of compressed sensing technique as sampling and data compression and reconstruction of signals using convex programming. Proceedings of the 21st Symposium on Signal Processing, Images and Artificial Vision (STSIVA). Bucaramanga, Columbia. 2016. 1–7.
|
| [12] |
Qi YT, Liu DH, Dunson D, et al. Multi-task compressive sensing with dirichlet process priors. Proceedings of the 25th International Conference on Machine Learning. Helsinki, Finland. 2008. 768–775.
|
| [13] |
常苗苗, 周金和. 基于改进贝叶斯压缩感知的正交频分复用系统信道估计. 计算机应用与软件, 2016, 33(2): 98-101. |
| [14] |
王玲玲, 齐丽娜. 特征字典与自适应联合的BCS-UWB信道估计. 计算机技术与发展, 2015, 25(12): 195-200. |
 2018, Vol. 27
2018, Vol. 27



