蝙蝠算法(Bat Algorithm, BA)是剑桥大学的Xin-She Yang基于蝙蝠的回声定位特性提出的一种群体智能搜索算法[1], 它完美结合了现有成功算法的主要优点[2], 具有模型简单、求解效率高、潜在并行性和分布式等特点[3,4], 其准确性和有效性优于遗传算法(Genetic Algorithm, GA)、粒子群优化(Particle Swarm Optimization, PSO)算法等经典算法[5,6], 已被应用于多个学科和工程领域[7–9]. 但BA没有变异机制, 难以保持种群的多样性, 容易陷入局部最优而发生早熟收敛, 致使求解精度较低; 它比PSO算法加强了局部搜索, 却也引起了后期收敛速度变慢的问题. 为了改善性能, 已研究出各种进化的、有效的变种蝙蝠算法[10], 如: 刘长平等通过引入逻辑自映射函数改进局部搜索能力, 提出了一种具有混沌搜索策略的蝙蝠优化算法[3,6]; 肖辉辉等将差分进化(Differential Evolution, DE)算法的变异、交叉和选择机制融合到基本蝙蝠算法中, 增强了种群的多样性、全局寻优能力和搜索能力, 形成了一种基于算法改进的蝙蝠算法[4]; 薛威力等通过动态调整参数和高斯扰动避免陷入局部最优, 提出了一种基于方差改进的蝙蝠算法[10]. 这些改进策略能够增强全局寻优能力、提高求解精度, 但同时对算法的简捷性和运行效率带来了不利影响.
本文提出一种基于权重因子、Cauchy分布随机数扰动和非线性规划的改进蝙蝠算法, 并将其应用于模糊层次分析中的判断矩阵一致性修正与因素权重计算, 取得了较为满意的结果.
1 蝙蝠算法及其改进 1.1 基本蝙蝠算法 1.1.1 蝙蝠算法的仿生原理BA是模拟自然界中蝙蝠利用超声波来探测猎物、绕过障碍物的一种随机搜索算法: 设有若干蝙蝠构成群体, 其个体映射为多维空间中的可行解, 将搜索最优解的过程模拟成蝙蝠个体移动和搜寻猎物过程; 利用求解问题的适应度函数值衡量蝙蝠所处位置的优劣, 将个体的优胜劣汰过程类比为优化过程中以较优的可行解替代较差可行解的迭代过程.
1.1.2 蝙蝠行为与算法描述将蝙蝠的回声定位行为按如下规则理想化:
(1) 所有蝙蝠利用超声波回音的感觉差异来区分食物/猎物和障碍物.
(2) 每只蝙蝠以速度vi、固定频率fmin(或波长λ)在位置xi(问题的解)随机飞行. 在搜索猎物时, 它们根据目标的远近调整波长λ(或频率f)、响度A和脉冲发射率r∈[0, 1].
(3) 响度A从最大值A0(正数)以一定方式衰减到最小值Amin.
对于求解非线性最小值函数min fx, 设蝙蝠群体规模为n, 在d维搜索空间中, 个体
| ${f_i} = {f_{\min }} + \beta ({f_{\max }} - {f_{\min }})$ | (1) |
| $v_i^{t + 1} = v_i^t + {f_i}(x_i^t - {x_*})$ | (2) |
| $x_i^{t + 1} = x_i^t + v_i^{t + 1}$ | (3) |
式中,
在优化过程中, 当满足条件时BA会自动转为局部搜索, 从当前最优解集中选择一个解, 并令每只蝙蝠在其邻域随机游走产生局部新解:
| $x' = x + \varepsilon {A^t}$ | (4) |
式中, x'是在当前最优解x附近产生的局部新解; ε∈[–1, 1]为d维随机向量;
蝙蝠在接近猎物的过程中, 其脉冲发射速率ri逐步提高, 同时声波的响度Ai逐渐降低, 并在发现猎物时达到最小. 相应迭代更新公式为:
| $r_i^{t + 1} = r_i^0[1 - \exp ( - \gamma t)],\;A_i^{t + 1} = \alpha A_i^t$ | (5) |
式中,
与其它群体智能优化算法相似的是, BA也未能避免易陷入局部最优、发生早熟收敛等问题, 因而对复杂高维多目标优化问题的求解精度不高. 究其原因, BA的寻优能力主要来自于蝙蝠个体间的相互作用, 由于个体没有变异机制, “超级蝙蝠”可能吸引其它个体迅速向其聚拢, 致使种群多样性严重下降; 同时, 随着蝙蝠个体在迭代过程中不断移向最优个体, 种群逐渐丧失进化能力, 故而后期的收敛速度大为降低甚至停滞. 由此可见, 对BA的改进应着眼于全程保持种群的多样性, 使其全局搜索能力和迭代后期的进化能力得以增强.
本文通过在BA中引入权重因子、Cauchy分布随机数扰动和非线性规划来改进其性能.
1.2.1 引入速度权重因子PSO算法以惯性权重w控制粒子对原有速度的继承性, 其值较大则粒子多样性好, 算法的全局搜索能力强; 反之则粒子移动性减弱, 局部搜索能力增强. 在实际应用中, 通常令w在指定取值区间内线性递减, 使PSO算法由前期强调全局搜索逐步转为后期重在局部搜索, 从而提高其整体优化性能.
蝙蝠算法与粒子群算法同属群智能优化算法, 二者的数学模型相近, 故其运行机制非常相似, 前者强化了局部搜索能力, 但可通过一定的参数设置演变为后者. 同时, 两种算法都存在早熟收敛、求解精度较低等问题, 因而可采用某些相同的策略来进行改进. 为此, 我们将PSO算法的惯性权重引入BA, 即为蝙蝠的速度增加一个权重因子w, 并令其在区间[wl, wu]线性递减, 则将式(2)变为如下式(6):
| $v_i^{t + 1} = {w_i}v_i^t + {f_i}(x_i^t - {x_*})$ | (6) |
显然, 式(2)是w≡1时的一种特殊情况[11]. 每次迭代时, 权重因子w按式(7)计算:
| ${w_i} = {w_u}({w_u} - {w_l}) \times \frac{{T - t}}{T}$ | (7) |
式中,
在基本BA流程中, 若均匀分布随机数
Cauchy分布的概率特性是两翼较长, 易于产生远离原点的随机数. 因此, 对蝙蝠位置进行Cauchy分布随机数扰动, 可较好地保持蝙蝠群体的多样性, 降低其陷入局部最优的概率, 从而提高算法的全局搜索能力, 有效防止早熟现象的发生. 扰动公式如下:
| $x_i^{t + 1} = x_i^t + x_i^t \times Cauchy$ | (8) |
式中,Cauchy表示标准Cauchy分布随机数, 其值为
将速度权重因子和Cauchy分布随机数扰动引入BA, 能改善其群体的多样性, 使其全局搜索能力得以提高, 但也可能由于蝙蝠移动性的增强而错过最佳解, 为此在算法中融入非线性规划函数, 以提高其局部搜索效率和整体优化精度, 并加快收敛速度.
非线性规划(Nonlinear Programming, NP)研究n元实函数在一组等式或不等式约束条件下的极值问题, 其目标函数和约束条件必有至少一个为未知量的非线性函数. 一般形式如下:
| $\begin{array}{*{20}{c}}{\min f(x)} & {s.t.\left\{ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{g_i}(x) = 0} & {i = 1,2, \cdots,p}\end{array}}\\{\begin{array}{*{20}{c}}{{h_j}(x) \le 0} & {j = 1,2, \cdots,q}\end{array}}\end{array}} \right.}\end{array}$ |
其中,
设计非线性规划函数fnp(或直接使用MATLAB的fmincon函数), 从变量的初始值开始搜索约束条件下的函数最小值, 在BA寻优过程中调用之: 传送x的当前值(蝙蝠位置)至fnp函数, 以之为初始值进行最佳函数值的搜索, 并将所得x的更好值返回BA继续迭代过程. 为避免对算法的运行速度产生明显影响, 可根据优化问题的实际需要, 每完成10次或20次迭代调用1次fnp函数.
1.3 改进蝙蝠算法的流程对于函数
(1) 设置算法参数. 确定蝙蝠数量n、变量维度d和最大迭代次数T, 设置搜索脉冲频率范围[fmin, fmax]、脉冲速率最大值r0及其增强系数γ、响度最大值A0及其衰减系数α, 给出变量空间[xl, xu]、蝙蝠速度范围[vl, vu]及其权重取值区间[wl, wu];
(2) 随机初始化蝙蝠位置xi、速度vi及搜索脉冲的频率fi、速率ri和响度Ai, 并根据适应度值找出当前最优个体位置x*;
(3) 根据式(1)更新脉冲频率fi, 依次由式(7)、式(6)计算蝙蝠的速度vi, 再按式(3)更新其位置xi, 即得新一代蝙蝠群体;
(4) 若随机数rand>ri, 则利用式(4)对当前最优蝙蝠位置进行随机扰动, 以扰动结果替换当前蝙蝠个体位置, 并计算其适应度值;
(5) 若蝙蝠位置得到改善且rand<Ai, 则接受所得新解, 并按式(5)更新脉冲响度Ai和发射速率ri. 否则按式(8)对蝙蝠位置施加Cauchy分布随机数扰动, 并进行越界处理;
(6) 根据适应度值找出蝙蝠群体的当前最优解和最优值;
(7) 若迭代次数t为20(或10)的倍数, 则调用非线性规划函数fnp加强局部搜索;
(8) 若达到最大迭代次数T(或优化精度ε), 停止搜索并输出全局最优解和最优值, 否则转到步骤(3)进入下一次迭代.
1.4 改进蝙蝠算法的测试采用标准测试函数, 在32位Windows7系统环境用MATLAB R2015b编程运行. 为了方便叙述和比较分析, 将仅引入速度权重和Cauchy分布随机数扰动的蝙蝠算法称为WCBA, 而将在此基础上融入非线性规划的改进算法简称WCNBA.
1.4.1 测试函数及参数设置选用5个标准测试函数, 其属性如表1所示.
| 表 1 5个测试函数 |
由于测试目的是将WCBA和WCNBA与BA进行比较, 以验证改进的有效性, 因此没有刻意对算法的参数进行优化, 而是统一设置为: n=40, T=300; fi∈[–1, 1], r0=0.75, A0=0.25, γ=α=0.9; vi∈[–1, 1], wi∈[1.0, 0.5].
同时, 我们也选取两种经典算法DE和PSO对一些函数进行测试, 以便进一步对蝙蝠算法及其改进效果进行对比分析. DE算法参数: 缩放因子F0=0.5, 交叉概率CR=0.25; PSO算法参数: 学习因子c1=c2=2.05, 速度取值区间v∈[–1, 1]. 结果表明, BA、WCBA和WCNBA全面优于DE和PSO算法, 其中单峰函数Sphere与多峰函数Rastrigin的求解迭代曲线分别如图1、图2所示.
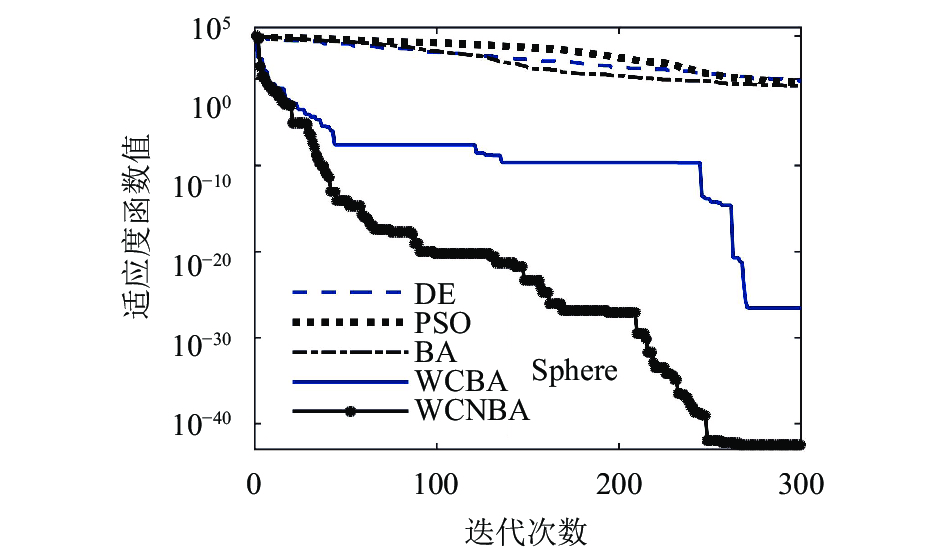
|
图 1 Sphere函数的求解迭代曲线 |
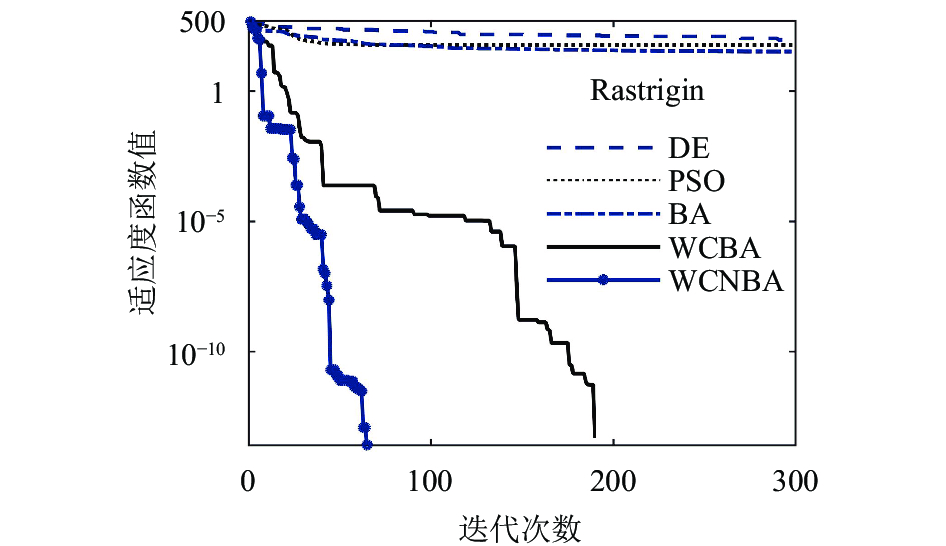
|
图 2 Rastrigin函数的求解迭代曲线 |
1.4.2 测试结果分析
每个测试函数独立运行30次, 取最优值、最差值、平均值和寻优成功率(获得理论最优值的次数占独立运行总次数的比率)进行比较, 所得结果如表2所示.
| 表 2 标准函数测试结果 |
从表2的测试结果看, 基于BA改进的WCBA和WCNBA皆显著优于基本蝙蝠算法. 其中, WCNBA对f1~f4都能完全收敛到理论最优值, 寻优成功率达到100%; 对于f5所得结果的平均值也非常接近理论最优值. 而WCBA对f4可完全收敛于理论最优值, 对f1和f3的寻优成功率则分别达到70.0%和33.3%, 对f2和f5所得结果也远优于BA. 因此, WCNBA是一种成功的BA改进算法, WCBA也具有一定的实用价值.
2 改进蝙蝠算法在模糊层次分析中的应用 2.1 模糊层次分析的步骤与关键环节层次分析法(Analytic Hierarchy Process, AHP)是将决策问题作为一个系统, 将其影响因素分解为目标、准则和方案等层次, 在此基础上将定性指标模糊量化, 遵照人类的思维、判断规律进行决策过程的一种实用方法. 因在处理复杂决策问题方面的实用性和有效性, AHP广泛应用于众多领域.
将AHP应用于模糊环境即为模糊层次分析法(Fuzzy Analytic Hierarchy Process, FAHP), 它应用模糊数学的隶属度来量化指标实测值, 从而解决层次分析中的模糊性(如因素类属之间不明晰、专家认识上的模糊性等)问题, 最大限度地降低人为因素的影响. FAHP的主要步骤为:
(1) 分析决策问题, 构建层次结构模型;
(2) 确定各层因素分别对其直接上级重要程度两两比较的隶属度, 以之建立模糊互补矩阵;
(3) 层次单排序(计算各层因素的相对权重);
(4) 方案总排序(方案层对目标层的合成权重).
模糊层次分析的数据量大、计算复杂繁琐, 其关键环节为计算因素权重, 它决定了决策结果的科学性、合理性和可信度. 计算因素权重的必要条件是模糊互补矩阵具有满意一致性, 因此还需先对其进行一致性检验和修正.
2.2 用改进蝙蝠算法求解因素权重对于模糊互补矩阵M=(mij)n×n(n为因素个数):
| $M = \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{m_{11}}} & {{m_{12}}} & \cdots & {{m_{1n}}}\end{array}}\\{\begin{array}{*{20}{c}}{{m_{21}}} & {{m_{22}}} & \cdots & {{m_{2n}}}\end{array}}\\ \vdots \\{\begin{array}{*{20}{c}}{{m_{n1}}} & {{m_{n2}}} & \cdots & {{m_{nn}}}\end{array}}\end{array}} \right]$ |
以0.1~0.9标度法表示其元素值, 则由模糊互补矩阵的定义可知: mii=0.5、mij+mji=1(i, j=1, 2,…, n分别为元素mij的行号和列号), 亦即M的对角线元素恒为0.5、其左下区域元素mji=1–mij. 因此, 在应用中只需确定右上区域元素mij, 即可算得左下区域元素mji.
传统做法是先用手工调整或数学变换法进行模糊互补矩阵的一致性检验与修正, 再以方根法、特征值法、和行归一化法和排序法等由模糊互补一致性矩阵计算因素权重, 其计算量大、繁琐费时. 应用WCNBA可将这两步工作合二为一, 即同时完成模糊互补矩阵的一致性检验、修正和相应的因素权重计算, 从而简化步骤、提高效率.
2.2.1 模糊互补一致性矩阵的充要条件定义1. 对于模糊互补矩阵M=(mij)n×n, 若
| ${m_{ij}} = {m_{ik}} - {m_{jk}} + 0.5$ | (9) |
则称M为加性一致性模糊互补矩阵. 由此可推知模糊互补一致性矩阵的充要条件为: 任意指定行与其余各行对应元素之差为某一常数.
定理1. 设M=(mij)n×n为模糊互补矩阵, 则M是模糊一致性矩阵的充要条件为: 存在一阶非负归一化向量w=(w1, w2,…, wn)T及正数α, 使得
| ${m_{ij}} = \alpha ({w_i} - {w_j}) + 0.5,\;\alpha \ge (n - 1)/2$ | (10) |
式中, α是对因素之间重视程度差异的度量, 其值小则决策者越重视这种差异; wi为因素权重.
2.2.2 用改进蝙蝠算法求解因素权重设R=(rij)n×n为修正后的模糊互补矩阵, 将式(9)的推论和式(10)结合起来, 可得模糊互补矩阵一致性的指标函数:
| $\begin{aligned}\min f(n) & = \sum\limits_{i = 1}^n {\sqrt {\frac{1}{n}{{\sum\limits_{j = 1}^n {({d_{ij}} - {{\bar d}_i})} }^2}} } /n \\& +\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{[0.5 + \alpha ({w_i} - {w_j}) - {r_{ij}}]}^2}/{n^2}} } \\& {\rm{s}}.{\rm{t}}.\;\left\{ {\begin{aligned}& {{r_{ii}} = 0.5,\;{r_{ij}} + {r_{ji}} = 1}\\& {{r_{ij}} = {r_{ik}} - {r_{jk}} + 0.5}\\& {{w_i} > 0,\;\sum\limits_{i = 1}^n {{w_i} = 1} }\\& {\alpha \ge (n - 1)/2}\end{aligned}} \right.\end{aligned}$ | (11) |
式中,
该指标函数值越小, 则R的一致性越好; 其值为0时, R具有完全一致性. 在实际应用中, 通常以f(n)<0.1为模糊互补矩阵具有满意一致性的标准.
应用WCNBA同步进行模糊互补矩阵的一致性修正和因素权重计算时, 以因素权重及矩阵右上区域(不含对角线)除第一行之外的元素为优化变量(共有(n–1)(n–2)/2+n个, n为因素个数), 以实数形式编码, 并设其搜索区间为[0, 1]; 以式(11)为适应度函数进行搜索, 当其值<0.1或达到最大迭代次数时, 返回因素权重和修正后的元素值.
2.2.3 应用实例在某校的课程建设质量评价中, 采用模糊层次分析法确定各级评价指标的主观权重, 其中有如下两个模糊互补矩阵[13]:
| $\begin{array}{l}{M_1} = \left[ {\begin{array}{*{20}{c}}{0.5} & {0.7} & {0.6} & {0.8}\\{0.3} & {0.5} & {0.4} & {0.7}\\{0.4} & {0.6} & {0.5} & {0.7}\\{0.2} & {0.3} & {0.3} & {0.5}\end{array}} \right]\\{M_2} = \left[ {\begin{array}{*{20}{c}}{0.5} & {0.4} & {0.4} & {0.2} & {0.3}\\{0.6} & {0.5} & {0.6} & {0.3} & {0.4}\\{0.6} & {0.4} & {0.5} & {0.3} & {0.3}\\{0.8} & {0.7} & {0.7} & {0.5} & {0.6}\\{0.7} & {0.6} & {0.7} & {0.4} & {0.5}\end{array}} \right]\end{array}$ |
用WCNBA进行M1、M2的一致性修正和因素权重计算, 算法的运行参数均按1.4.1设置, 其寻优迭代过程如图3所示, 所得结果如表3所示.
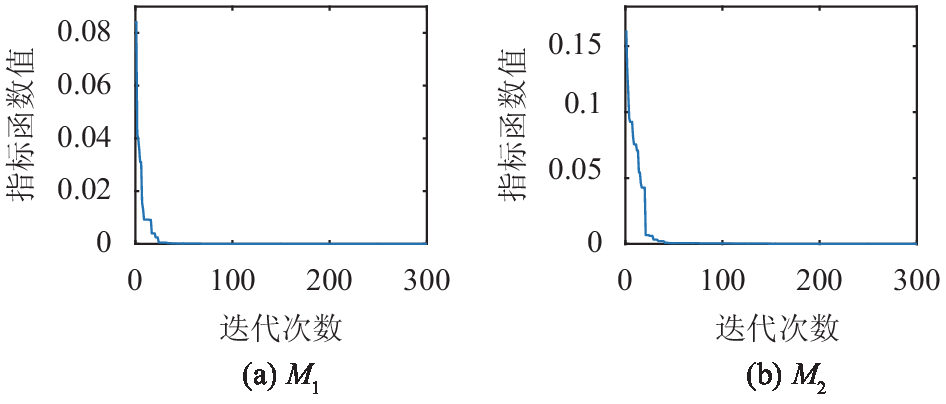
|
图 3 用WCNBA对M1、M2的寻优迭代过程 |
将表3与M1、M2的数据对比可知, M1的(2, 4)和M2的(2, 3)、(3, 5)位置处的元素得到了修正, 于是相应的模糊互补一致性矩阵R1和R2如下:
| $\begin{array}{l}{R_1} = \left[ {\begin{array}{*{20}{c}}{0.5} & {0.7} & {0.6} & {0.8}\\{0.3} & {0.5} & {0.4} & {\underline {0.6} }\\{0.4} & {0.6} & {0.5} & {0.7}\\{0.2} & {\underline {0.4} } & {0.3} & {0.5}\end{array}} \right]\\{R_2} = \left[ {\begin{array}{*{20}{c}}{0.5} & {0.4} & {0.4} & {0.2} & {0.3}\\{0.6} & {0.5} & {\underline {0.5} } & {0.3} & {0.4}\\{0.6} & {\underline {0.5} } & {0.5} & {0.3} & {\underline{\underline {0.4}} }\\{0.8} & {0.7} & {0.7} & {0.5} & {0.6}\\{0.7} & {0.6} & {\underline{\underline {0.6}} } & {0.4} & {0.5}\end{array}} \right]\end{array}$ |
| 表 3 M1、M2的一致性修正和因素权重计算结果 |
3 结论
本文针对基本蝙蝠算法在寻优过程中难以保持种群的多样性、易发生早熟收敛、求解精度较低等问题, 通过引入速度权重因子、施加Cauchy分布随机数扰动和融入非线性规划函数等措施, 设计并实现了改进的蝙蝠算法WCBA和WCNBA. 经用标准函数测试, 并在模糊层次分析中应用, 结果表明改进的蝙蝠算法显著优于基本蝙蝠算法.
| [1] |
Yang XS. A new metaheuristic bat-inspired algorithm. González JR, Pelta DA, Cruz C, et al. Nature Inspired Cooperative Strategies for Optimization. Berlin Heidelberg: Springer, 2010. 65–74.
|
| [2] |
李煜, 马良. 新型全局优化蝙蝠算法. 计算机科学, 2013, 40(9): 225-229. |
| [3] |
刘长平, 叶春明. 具有混沌搜索策略的蝙蝠优化算法及性能仿真. 系统仿真学报, 2013, 25(6): 1183-1188, 1195. |
| [4] |
肖辉辉, 段艳明. 基于DE算法改进的蝙蝠算法的研究及应用. 计算机仿真, 2014, 31(1): 272-277, 301. |
| [5] |
贺兴时, 丁文静, 杨新社. 基于模拟退火高斯扰动的蝙蝠优化算法. 计算机应用研究, 2014, 31(2): 392-397. |
| [6] |
刘长平, 叶春明, 刘满成. 来自大自然的寻优策略: 像蝙蝠一样感知. 计算机应用研究, 2013, 30(5): 1320-1322, 1356. |
| [7] |
盛晓华, 叶春明. 蝙蝠算法在PFSP调度问题中的应用研究. 工业工程, 2013, 16(1): 119-124. |
| [8] |
李枝勇, 马良, 张惠珍. 0-1规划问题的元胞蝙蝠算法. 计算机应用研究, 2013, 30(10): 2903-2906, 2935. DOI:10.3969/j.issn.1001-3695.2013.10.005 |
| [9] |
张蓉. 蝙蝠算法优化最二乘支持向量机的网络入侵检测. 激光杂志, 2014, 35(11): 101-104. |
| [10] |
薛威力, 贺兴时, 杨新社. 蝙蝠算法的一种改进. 哈尔滨商业大学学报(自然科学版), 2016, 32(6): 706-712. |
| [11] |
李枝勇, 马良, 张惠珍. 蝙蝠算法收敛性分析. 数学的实践与认识, 2013, 43(12): 182-190. DOI:10.3969/j.issn.1000-0984.2013.12.026 |
| [12] |
胡振. QPSO混合算法在PID控制器优化中的应用. 计算机系统应用, 2014, 23(10): 233-238. DOI:10.3969/j.issn.1003-3254.2014.10.042 |
| [13] |
陈素彬, 胡振. 高职院校分析化学课程建设的量化评价方法. 化学教育, 2017, 38(8): 44-50. |
 2018, Vol. 27
2018, Vol. 27


