蛋白质是生物体内生命活动的主要承担者, 是一切生命活动的基础, 它的生理功能除了体现在氨基酸构成上还体现在它的空间结构上[1]. 因此, 预测蛋白质结构是生物信息学领域的一个重要任务. 通常, 蛋白质结构包括4个层次[2]: 一级结构即氨基酸的排列顺序; 二级结构主要是由氢键维持的α-螺旋和β-折叠; 三级结构是完全折叠的蛋白质的空间结构残基的立体排列模式; 四级结构是多个蛋白质亚基组成的蛋白质复合体的结构(即蛋白质之间的交互作用). 蛋白质二级结构是联系蛋白质一级结构和三级结构的纽带, 而且也是从一级结构预测其三级结构的关键步骤[3,4]. 当蛋白质二级结构预测正确率达到80%时, 就可以准确预测一个蛋白质分子的三维空间结构[5]. 可见, 蛋白质二级结构预测已经成为研究蛋白质结构和功能的重要手段.
由于已测定结构的蛋白质数量远远小于已知的蛋白质序列数量[6], 并且传统的生物实验测定蛋白质结构的方法花费昂贵且耗时时间较长. 因此, 采用数据驱动的方法(如机器学习技术)来预测未知的蛋白质的结构和功能广受青睐. 在过去的一段时间内, 很多方法被提出来用于蛋白质结构类的预测. 而影响蛋白质结构类预测效果的关键因素主要集中在两个方面上: 一是分类预测算法, Zhou等人使用神经网络[7], Mandle等人使用支持向量机[8], Wang和Peng等使用深度卷积神经网络技术来进行蛋白质结构预测[9]; 二是蛋白质特征信息提取, 如Chou等人提出的伪氨基酸组成(PseAA法)[10–12], Cao等人提出的基于简化PSSM与蛋白质结构位置信息的特征表示算法[13].
一般的预测方法通常使用BLOSUM62矩阵构造特征向量, 对蛋白质进化过程中存在的氨基酸位点突变现象缺乏考虑. 本文提出一种新的特征表示方法, 对于一条蛋白质序列, 同时使用多种进化趋异度的矩阵来表示蛋白质序列, 更全面的考虑了残基替换的可能性. 不同的进化矩阵对不同相关程度的蛋白质序列的敏感性不同. 这使得多重进化矩阵这种蛋白质序列特征表示方法, 不仅可以很好地反映序列中氨基酸的位置信息, 而且全面考虑序列内部近相关和远相关蛋白质区域[14]之间的相互影响. 本文结合交叉验证法和网格搜索法来确定实验参数, 先在大范围大步距粗搜, 初步确定一个最优参数区间, 之后在此区间进行小步距精搜, 结合网格搜索法和交叉验证法共同确定实验参数. 在数据集RS126、CB513和25PDB上进行的多组实验, 表明本文所提出的基于多重进化矩阵的特征向量构造方法能够有效提高蛋白质二级结构预测精度.
1 相关知识 1.1 位置特异性矩阵通过蛋白质序列的位置特异性打分矩阵而不是仅依靠序列来预测蛋白质结构, 是公认的提高预测精度的方法. 序列的多重比对反映了蛋白质家族的共同特征, 提取了结构的保守信息及家族中特定的残基替换模式, 同时多序列比对所携带的进化信息也表明了蛋白质进化过程中的相互作用[15].
本文主要采用了BLAST的本地化使用来获得蛋白质序列的profile. 将BLAST软件包下载到本地以后, 可以通过命令行的形式去调用相应的可执行文件. 在这里, 我们使用PSI-BLAST程序(h=0.001, j=3)搜索和调整无冗余的NR数据库. 该程序将返回一个20维矢量的PSSM[16], 其值是20个氨基酸保守的突变分数. 这样得到的PSI-BLAST profile是一个L×20的矩阵(其中L是蛋白质序列的长度), 也称之为位置特异性打分矩阵(Position-Specific Score Matrix, PSSM). PSSM矩阵形式如公式(1)所示.
| ${\rm{PSSM}}_s \!=\!\! \left[\! {\begin{array}{*{20}{l}}{{P_{1 \to 1}}} & {{P_{1 \to 2}}} & \cdots & {{P_{1 \to j}}} & \cdots & {{P_{1 \to 20}}}\\{{P_{2 \to 1}}} & {{P_{2 \to 2}}} & \cdots & {{P_{2 \to j}}} & \cdots & {{P_{2 \to 20}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\{{P_{i \to 1}}} & {{P_{i \to 2}}} & \cdots & {{P_{i \to j}}} & \cdots & {{P_{i \to 20}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\{{P_{L \to 1}}} & {{P_{L \to 2}}} & \cdots & {{P_{L \to j}}} & \cdots & {{P_{L \to 20}}}\end{array}}\! \right]\!\!$ | (1) |
PSSM矩阵的每一行代表在查询序列的相应位置发生在氨基酸替代的对数似然得分. 位于矩阵第i行第j列的元素Pij表示在进化过程中查询序列的第i个位置的氨基酸突变成j类氨基酸的得分.
1.2 二级结构划分标准蛋白质二级结构通常分为8类: G(310-helix), H(α-helix), I(π-helix), B(isolated β-bridge), E(β-stand), S(bend), T(hydrogen bonded turn)和rest(apparently random conformations). 主流的PSSP思想会将这8类结构归纳为3种构象(H、E和C). 通常情况下, H、E和C三种构象之间没有明确的界限而且也没有统一的标准去划分这三种构象. 然而在1999年, Cuff和Barton两位学者证实了划分方案可以影响最后的预测精度, 所以人们希望找到一种划分方案可以获得更高的预测精度. 由此, 蛋白质二级结构字典法(DSSP[17])获得了广泛的认可. 该方法依据已知的氢键相连的部分划分二级结构. 本文选用DSSP方法, 将8类结构明确归纳为: H、G属于Helices, 记作H; E、B属于Sheets, 记作E; G、S、T、C、I属于Coils, 记作C.
2 基于多重进化矩阵的特征向量构造方法在实际中, 蛋白质的结构是不断折叠式的, 某个残基不仅与它相邻的残基发生作用, 还可能与它在序列上相差较远的某些残基发生作用, 且蛋白质进化过程中氨基酸位点存在突变的可能. PAM矩阵和BLOSUM矩阵就反映了蛋白质中存在的氨基酸突变.
因PAM矩阵和BLOSUM矩阵都是PSI-BLAST程序中的打分标准, 不同的打分矩阵对于评价氨基酸突变是不同的[18,19], 例如PAM250矩阵假设每100个氨基酸发生250次点突变, PAM矩阵存在从PAM1到PAM250的情况. 由于PAM矩阵是基于近相关蛋白比对得到的打分矩阵, BLOSUM矩阵是基于观测到的远相关蛋白对比得到的打分矩阵. 本文参考了PAM矩阵和BLOSUM矩阵之间的相互关系[20], 如图1所示, 设计了多重进化矩阵编码方式. 为更详细的描述氨基酸位点发生突变的可能性和序列内部近距离和远距离的氨基酸之间的相互影响, 选择了低趋异度矩阵PAM30和高趋异度矩阵PAM250和BLOSUM62矩阵三种不同趋异度的进化矩阵来表达蛋白质序列.

|
图 1 PAM矩阵和BLOSUM矩阵概要 |
首先将蛋白质序列送入PSI-BLAST程序, 通过调整参数, 得到广泛使用的BLOSUM62矩阵、低趋异度矩阵BLOSUM90和高趋异度矩阵PAM250. 将得到的三种不同趋异度的进化矩阵对齐特征维度, 组合得到60维的向量表示原来的蛋白质序列, 考虑临近残基的影响, 采用滑动窗口法对所得特征向量进行处理, 设置滑动窗口为13, 得到一个780维向量表示原来的序列, 构成多重进化矩阵特征.
为了能够用计算方法进行训练和预测, 需要将相差较大的原始值进行规范化处理. 本文利用公式(2)把多重进化矩阵的元素标准化到0~1之间.
| $f(x) = \frac{1}{{1 + {e^{ - x}}}}$ | (2) |
其中x是多重进化矩阵中元素的原始值.
3 蛋白质二级结构预测框架为了在构造特征向量时能更好的反映蛋白质序列中氨基酸残基存在突变的可能性, 且考虑预测过程中存在分类器参数选择困难及可靠性差等问题, 本文提出基于多重进化矩阵的蛋白质二级结构预测方法, 其具体过程如下:
1) 首先要将BLAST本地化. 下载蛋白质NR数据库及BLAST程序本地软件包, 对BLAST进行本地配置.
2) 计算蛋白质序列的位置特异性打分矩阵(PSSM)矩阵, 设置PSI-BLAST程序的参数为(-num_iterations: 3, -eavlue: 0.001, -matrix: BLOSUM62), 得到该参数条件下的PSSM矩阵.
3) 调整PSI-BLAST程序参数, 将matrix分别设置为BLOSUM90和PAM250, 计算该参数条件下的PSSM矩阵.
4) 将3)中得到的三种进化矩阵对齐特征维度, 组合得到60维的向量来表示原来的蛋白质序列. 采用滑动窗口法处理向量, 设置滑动窗口为13, 得到一个780维向量来表示原来的蛋白质, 构成多重进化矩阵特征, 对矩阵进行标准化处理.
5) 利用网格搜索法和K折交叉验证来优选实验参数. 选取强分类器多分类支持向量机M-SVMCS来说明实验过程:
① 设定网格搜索的变量(c, p)的范围以及搜索步距, 选择使分类准确率最高的一组c和p;
② 在寻得了局部最优参数之后, 再在这组参数附近选择一个小区间, 采用小步距进行二次精搜, 再次选择使分类准确率最高的一组c和p;
③ 涉及的所有参数对都用7折交叉验证进行实验, 按数据集条数平均分成7份, 每次选择其中6份做训练集, 剩下的1份做测试集, 重复7次;
④ 上述提到的分类准确率的参数对按照以下原则确定: 若参数选择过程中有多组c和p对应于最高的验证分类准确率, 则选取能够达到最高验证分类准确率中参数c最小的那组c和p作为最佳的参数; 如果对应最小的c有多组p, 就选取搜索到的第一组c和p作为最佳参数对;
6) 按照5)中获得的最优参数模型, 输入结构未知的蛋白质序列特征, 预测各个位点残基二级结构.
4 实验与结果分析 4.1 数据集为了检验模型的预测精确性, 选择数据集要慎重, 需要结合机器学习和生物学方面的知识. 伴随着PDB等主要蛋白质结构数据库中的蛋白质结构资源的日益丰富, 可用的蛋白质二级结构预测的样本也越来越多. 出于对实验结果的公平及公正性的考虑, 本文选择三个广泛应用的低同源性数据集RS126[21]、CB513[22]和25PDB[23]作为本文的实验数据集, 序列相似性均低于25%. RS126数据集含有126条非同源蛋白质序列. CB513数据集含有513条非同源蛋白质序列. 25PDB数据集含有 1673条非同源蛋白质和从PDB中下载和扫描的高分辨率结构域.
4.2 参数选择为了证明本文提出的多重进化矩阵是一种有效特征向量表示方法, 本文选择了两种弱分类器Logistics、RandomForest和一种强分类器MSVMpack进行实验. 其中Logistics和RandomForest来自WEKA软件, M-SVMCS来自MSVMpack软件[24]. 三种分类器都是通过网格搜索法来挑选实验参数. 为了对分类器参数进行优化, 且保证优化结果的可靠性, 本方法结合七折交叉验证与网格搜索法来确定实验参数.
经过多组实验, 对所获得的实验结果进行对比, 选择其中最好的一组作为最优参数. 对于数据集CB513和25PDB我们将针对不同分类算法得到的最优参数汇总如表1所示.
| 表 1 最优参数结果表 |
4.3 结果评价标准
关于蛋白质二级结构预测结果的评价标准有很多种. 目前在国际上大多使用以下几种标准:
(1) 整体预测准确率Q3
目前应用最广泛的准确率, 它指的是被正确预测的3种二级结构(残基)的总百分比, 可由公式(3)计算得出.
| ${Q_i} = \frac{P_{\rm{H}}+P_{\rm{E}}+P_{\rm{C}}}{N_{\rm{H}}+N_{\rm{E}}+N_{\rm{C}}}*100\% $ | (3) |
其中, NH、NE和NC分别表示序列中二级结构为H、E和C的残基的总个数, PH、PE和PC分别表示被正确预测为H、E和C构象的残基个数.
(2) 三态预测准确率Qi
我们用Qi来表示每种二级结构被正确预测为H, E或C构象的预测准确率. 可由公式(4)计算得出:
| ${Q_i} = \frac{{{P_i}}}{{{N_i}}}*100\% ,i \in \{\rm{ H,E,C}\} $ | (4) |
其中, Pi是待预测序列中被正确预测的处于i构象的残基数目, Ni是待预测序列中被正确预测的处于i构象的残基数目, i属于H构象、E构象或C构象.
根据本文第4节的方法, 我们在RS126、CB513和25PDB数据集上进行实验. 在RS126数据集上三个独立分类器得到的整体预测准确率分别为67.86%、67.90%和73.90%, 其各项独立指标如表2所示. 在CB513数据集上三个独立分类器得到的整体预测准确率分别为65.53%、71.32%和75.50%, 其各项独立指标如表3所示. 在25PDB数据集上三个独立分类器得到的整体预测准确率分别为68.57%、72.62%和76.72%, 其各项独立指标如表4所示.
| 表 2 RS126数据集使用BLOSUM62矩阵预测结果(%) |
| 表 3 CB513数据集使用BLOSUM62矩阵预测结果(%) |
| 表 4 25PDB数据集使用BLOSUM62矩阵预测结果(%) |
然后, 我们组合三种不同进化趋异度的矩阵, 作为三个独立分类器的输入向量, 通过网格搜索法和7折交叉法优选实验参数, 获得优化参数模型, 输入结构未知的蛋白质序列特征, 预测各个位点残基二级结构. 对数据集RS126使用三种分类器获得的整体预测准确率分别是66.40%、68.08%和74.05%, 各类别的预测准确率如表5所示. 对数据集CB513使用三种分类器获得的整体预测准确率分别是69.18%、71.89%和75.92%, 各类别的预测准确率如表6所示. 通过对比表2和表5可以看出, 相比于传统的实验方法, 多重进化矩阵这种表示方法在RS126数据集上分别高出了-1.37%、0.18% 和0.15%. 通过对比表3和表6可以看出, 相比于传统的实验方法, 多重进化矩阵这种表示方法在CB513数据集上分别高出了3.65%、0.57% 和0.42%. 而对于数据集25PDB得到的整体预测准确率分别是70.57%、73.16%和78.05%, 各类别的预测准确率如表5所示. 通过对比表4和表7可以看出, 相比于传统的实验方法, 多重进化矩阵这种表示方法在25PDB数据集上分别高出了2.00%、0.54% 和1.33%. 各表中整体预测准确率提高的值用粗体显示.
| 表 5 RS126数据集使用多重进化矩阵预测结果(%) |
| 表 6 CB513数据集使用多重进化矩阵预测结果(%) |
| 表 7 25PDB数据集使用多重进化矩阵预测结果(%) |
为了更为直观的体现本文方法的有效性, 本文将在RS126数据集、CB513数据集和25PDB数据集上使用不同算法得到的整体预测准确率表示成图2、图3和图4, 从中可以看出, 本方法相对于原BLOSUM62蛋白质序列表示方法, 除去对RS126数据集使用Logistics分类器得到的结果有所下降, 在其他对比实验中得到的整体预测准确率均有提高. 对于这种现象, 由于:
(1) 相对于CB513数据集和25PDB数据集, RS126数据集数据量比较少, 包含的蛋白质种类少 .
(2) Logistics分类器的分类精度受样本数据量的影响, 当样本数量较小时, 结果存在的风险较大.
综合这两种因素, 我们认为, 对于逻辑回归分类器, 使用多重进化矩阵反而分类精度有所下降这种现象是正常的, 不能否认多重进化矩阵是一种有效的蛋白质序列特征表示方法. 我们将对于三个数据集的使用M-SVMCS分类器得到的结果汇总, 如图5所示. 从表2至表7和图5可以看出, 在整体预测准确率上, 本文方法比BLOSUM62矩阵表示方法在不同数据集上分别提高了 0.15%、0.42%和1.33%, 对于数据集RS126提升较小, 对于25PDB数据集提升较大. 说明多分类支持向量机比较适用于大样本数据集, 而对于小样本数据集效果并不明显.

|
图 2 不同方法在数据集RS126的整体预测准确率 |

|
图 3 不同方法在数据集CB513的整体预测准确率 |
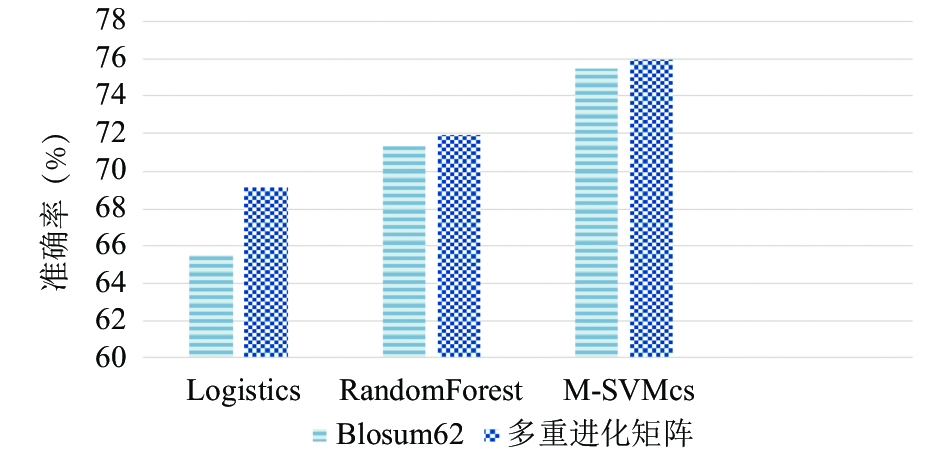
|
图 4 不同方法在数据集25PDB的整体预测准确率 |

|
图 5 M-SVMCS分类器在不同数据集的整体预测准确率 |
5 结语
本文根据蛋白质序列不同进化趋异度之间的关系, 组合PAM矩阵和BLOSUM矩阵, 设计了一种新的方法来构成特征向量表示蛋白质序列信息; 选用Logistics、RandomForest和M-SVMCS机器学习模型作为预测工具, 采用交叉验证法和网格搜索法相结合来确定实验参数, 预测各个位点残基二级结构. 在数据集RS126、CB513和25PDB上开展的对比实验, 表明本文所提出基于多重进化矩阵的蛋白质特征向量构造方法能够有效提高蛋白质二级结构的预测精度.
在下一步的工作中, 我们可以从下面几点做出改进: (1)深入研究蛋白质信息特征提取算法, 加入对蛋白质二级结构特征信息的描述; (2)尝试利用特征选择算法优选特征, 降低特征向量维度, 提高分类器计算速度. 在分类算法上进行可能的改进也是下一步研究的重点.
| [1] |
Jones DT. Protein structure prediction in the postgenomic era. Current Opinion in Structural Biology, 2000, 10(3): 371-379. DOI:10.1016/S0959-440X(00)00099-3 |
| [2] |
泽瓦勒贝, 鲍姆. 理解生物信息学. 李亦学, 郝沛, 译. 北京: 科学出版社, 2012.
|
| [3] |
Floudas CA. Computational methods in protein structure prediction. Biotechnology and Bioengineering, 2007, 97(2): 207-213. DOI:10.1002/(ISSN)1097-0290 |
| [4] |
Khoury GA, Smadbeck J, Kieslich CA, et al. Protein folding and de novo protein design for biotechnological applications. Trends Biotechnology, 2014, 32(2): 99-109. DOI:10.1016/j.tibtech2013.10.008 |
| [5] |
张海霞, 唐焕文, 张立震, 等. 蛋白质二级结构预测方法的评价. 计算机与应用化学, 2003, 20(6): 735-740. |
| [6] |
Lee D, Redfern O, Orengo C. Predicting protein function from sequence and structure. Nature Reviews Molecular Cell Biology, 2007, 8(12): 995-1005. DOI:10.1038/nrm2281 |
| [7] |
Cai YD, Zhou GP. Prediction of protein structural classes by neural network. Biochimie, 2000, 82(8): 783-785. DOI:10..1016/S0300-9084(00)01161-5 |
| [8] |
Mandle AK, Jain P, Shrivastava SK. Protein structure prediction using support vector machine. International Journal on Soft Computing, 2012, 3(1): 67-78. DOI:10.5121/ijsc |
| [9] |
Wang S, Peng J, Ma JZ, et al. Protein secondary structure prediction using deep convolutional neural fields. Scientific Reports, 2016, 6: 18962. DOI:10.1038/srep18962 |
| [10] |
Lu Z, Szafron D, Greiner R, et al. Predicting subcellular localization of proteins using machine-learned classifiers. Bioinformatics, 2004, 20(4): 547-556. DOI:10.1093/bioinformatics/btg447 |
| [11] |
Chou KC, Cai YD. Predicting protein localization in budding yeast. Bioinformatics, 2005, 21(7): 944-950. DOI:10.1093/bioinformatics/bti104 |
| [12] |
Cai YD, Chou KC. Predicting 22 protein localizations in budding yeast. Biochemical and Biophysical Research Communications, 2004, 323(2): 425-428. DOI:10.1016/j.bbrc.2004.08.113 |
| [13] |
Wang JR, Wang C, Cao JJ, et al. Prediction of protein structural classes for low-similarity sequences using reduced PSSM and position-based secondary structural features. Gene, 2015, 554(2): 241-248. DOI:10.1016/j.gene.2014.10.037 |
| [14] |
梅娟, 赵吉, 傅毅. 基于图聚类和序列信息的蛋白质远同源性探测. 计算机与应用化学, 2015, 32(8): 945-950. |
| [15] |
Wang L, You ZH, Xia SX, et al. Advancing the prediction accuracy of protein-protein interactions by utilizing evolutionary information from position-specific scoring matrix and ensemble classifier. Journal of Theoretical Biology, 2017, 418: 105-110. DOI:10.1016/j.jtbi.2017.01.003 |
| [16] |
Ben-Gal I, Shani A, Gohr A, et al. Identification of transcription factor binding sites with variable-order Bayesian networks. Bioinformatics, 2005, 21(11): 2657-2666. DOI:10.1093/bioinformatics/bti410 |
| [17] |
Sebastiani F. Text categorization. Rivero LC, Doorn JH, Ferraggine VE. Encyclopedia of Database Technologies and Applications. Hershey, US: Idea Group Reference, 2005. 683–687.
|
| [18] |
Ortuño FM, Valenzuela O, Prieto B, et al. Comparing different machine learning and mathematical regression models to evaluate multiple sequence alignments. Neurocom-puting, 2015, 164: 123-136. DOI:10.1016/j.neucom.2015.01.080 |
| [19] |
Lal D, Verma M. Large-scale sequence comparison. Keith JM. Bioinformatics: Volume I: Data, Sequence Analysis, and Evolution. New York: Springer, 2017. 191–224.
|
| [20] |
乔纳森•佩夫斯纳. 生物信息学与功能基因组学. 孙之荣, 译. 北京: 化学工业出版社, 2006.
|
| [21] |
Rost B, Sander C. Prediction of protein secondary structure at better than 70% accuracy. Journal of Molecular Biology, 1993, 232(2): 584-599. DOI:10.1006/jmbi.1993.1413 |
| [22] |
Cuff JA, Barton GJ. Evaluation and improvement of multiple sequence methods for protein secondary structure prediction. Proteins Structure Function and Bioinformatics, 1999, 34(4): 508-519. DOI:10.1002/(ISSN)1097-0134 |
| [23] |
Kurgan LA, Homaeian L. Prediction of structural classes for protein sequences and domains-impact of prediction algorithms, sequence representation and homology, and test procedures on accuracy. Pattern Recognition, 2006, 39(12): 2323-2343. DOI:10.1016/j.patcog.2006.02.014 |
| [24] |
http://www.Loria.fr/lauer/MSVMpack.
|
 2018, Vol. 27
2018, Vol. 27


