情绪是一种综合了人的感觉, 思想和行为的状态, 它包括人对外界或自身刺激的心理反应, 也包括伴随这种心理反应的生理反应, 在人们的日常工作和生活中, 情绪的作用无处不在. 因此, 基于人类的视觉特征和脑电特征, 采用计算机技术, 对情绪特征进行归类的情绪识别成为人机交互、情感计算、智能控制、机器视觉、图像处理与模式识别等领域的重要研究课题.
1.2 研究现状(1)关于人脸表情识别的研究
20世纪70年代美国心理学家Ekman和Friesen对现代人脸表情识别做出了开创性的工作[1]. Ekman定义了人类的6种基本表情: 高兴、生气、吃惊、恐惧、厌恶和悲伤, 确定了识别对象的类别; 其次是建立了面部动作编码系统 (Facial Action Coding System, FACS ). Shao等人在2015年提出一种基于子集选择的面部识别的方法, 用来提取人脸的特征[2]. Hu等人在2016年提出一种从单一人脸图像中进行3D人脸重建的方法, 用于进行人脸信息的扩充[3]. 2003年, 北京科技大学的王志良教授领导的团队, 将人脸表情识别算法应用于机器人的情感控制研究中[4]. 人脸表情识别的研究具有很大的开发潜力. 但检测出准确的表情并不总可以代表人的真正情绪, 因为人可以伪装表情.
(2)关于基于脑电的情绪识别研究
对于提取出的脑电特征, 如何从脑电特征中学习出情绪状态的模型, 是脑电能否在情绪识别中得到应用是关键性的一步. Murugappan等人利用模糊C均值和模糊K均值的方法对高兴、厌恶、恐惧三种情绪进行聚类, 并通过对聚类效果的观察, 选择能对情绪进行区分的最少特征集合[5]. Bos利用费雪判别分析, 针对正向、负向、兴奋、平静情绪中每一类分别训练一个分类器, 使得正向情绪的分类准确率为37/39, 兴奋、平静情绪分类准确率为38/39[6]. Yazdani等人利用贝叶斯线性判别分析, 将脑电特征针对喜悦、愤怒、厌恶、悲伤、惊讶、恐惧等六种情绪进行了分类, 达到80%以上的准确率[7]. Pertrantonakis和Hadjileon-tiadis利用二次判别分析(Quadratic Discriminant Analysis, QDA)以及SVM对情绪在愉快、惊讶、生气、恐惧、厌恶、悲伤六种类别下进行分类, 分别达到了62.3%和83.33%的准确率[8]. 但是基于脑电的情绪识别方法, 存在信号难以提取的问题. 在采集脑电信号时, 会存在较大的其他电位干扰(如肌电, 眼电等).
(3) 关于利用信息融合技术的研究
尽管基于单一模态的情绪识别方法上携带着准确的情绪信息, 但是信号强度十分微弱, 所以在提取过程中要求较高. 近年来, 随着多源异类信息融合处理领域的发展, 可以将来自多类别参考情绪状态的特征进行融合. 利用不同类别的信号相互支持, 通过对互补信息进行融合处理, 可以得到很大改善. 因此, 人们开始利用人脸表情、语音、眼动、姿态和生理信号等多个通道的情绪信息之间的互补性来研究识别问题, 即基于多模态的情绪识别. 多模态信息融合识别相对于单一信号识别无疑是可以提高识别准确率的.
本文的工作就是融合人脸图像和脑电识别的结果, 以提高情绪识别的准确率.
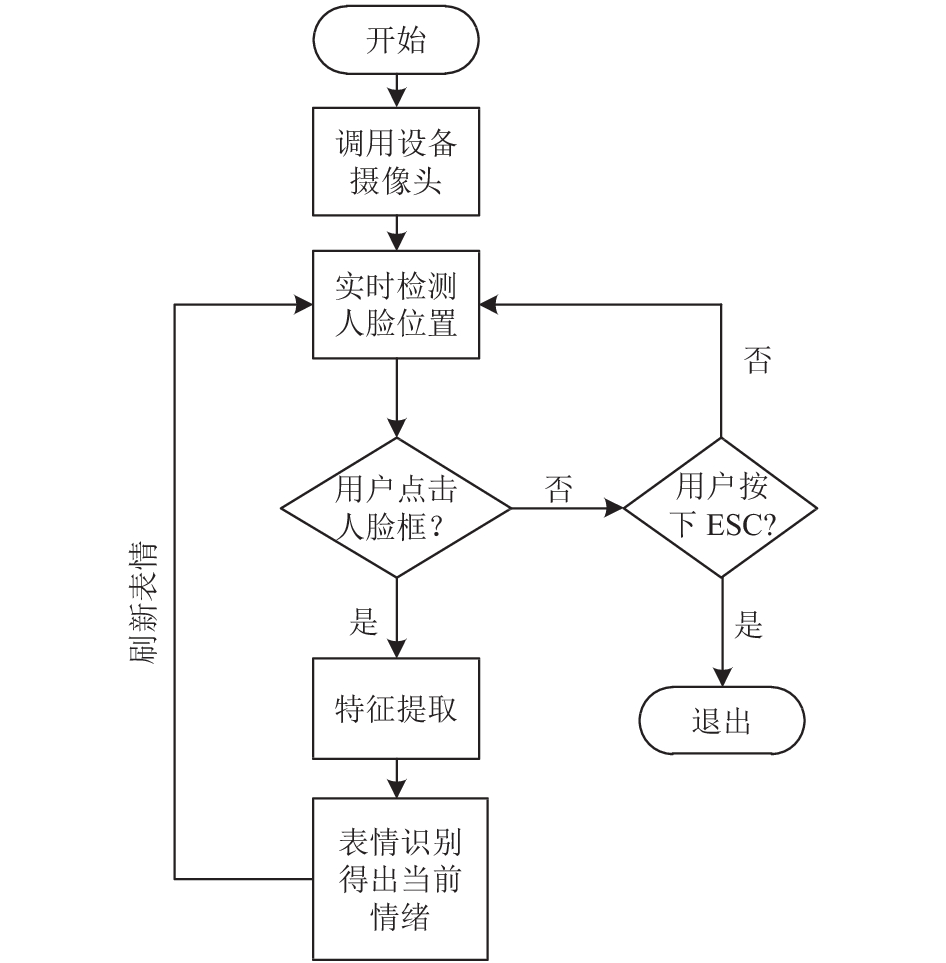
2 人脸表情识别的基本原理和实现 2.1 人脸表情识别过程程序通过摄像头采集到图像, 通过基于Haar特征值的Adaboost算法, 实时检测人脸位置. 利用主成分分析(Principal Component Analysis, PCA)对提取人脸特征值进行降维处理. 将降维后的特征值利用卷积神经网络进行分类. 详细过程见图1. 下面重点讲述Adaboost算法, PCA降维和卷积神经网络算法.
|
图 1 人脸表情识别流程图 |
2.2 使用基于Haar特征值的Adaboost算法进行人脸检测基本原理
基于人脸图像的人脸检测方法, 采用基于Haar特征值的Adaboost算法[9], 它实际上是Boosting算法的一个应用, Haar分类器用到了Boosting算法中的Adaboost算法, 把Adaboost算法训练出的强分类器进行了级联.
Adaboost是一种迭代算法, 其核心思想是针对一个训练数据集
其算法本身是通过改变数据分布来实现的. 通过每次训练集之中每个样本分类结果是否准确来训练弱分类器. 并通过上一次的总体分类准确率来确定每个弱分类器在强分类器中的权重, 最终将多个弱分类器结合成强分类器.
将提取到的Haar特征值作为输入, 利用Adaboost算法进行分类器训练, 最终得出可用于人脸检测的分类器.
2.3 表情特征提取表情特征提取是人脸表情识别中最重要的部分, 有效的表情特征提取工作将使识别的性能大大提高. 通过对大量文献的总结, 可知好的表情特征提取结果应该具备以下几个条件: (1) 可完整表示出人脸表情的本质特征; (2) 可通过灰度处理, 高斯滤波等方法去除噪声、光照及其他与表情无关的干扰信息; (3) 数据表示形式紧凑, 可避免过高的维数(常见的方法有PCA和LDA, 本文利用PCA进行数据降维操作); (4) 不同类别表情特征之间有较好的区分性. 要得到满足这些条件的表情特征, 特征提取的过程可能需要数个步骤来完成. 首先, 利用某种形式的信息来获得表情的原始特征, 如特征形状与几何关系, 局部纹理, 光流场等, 这一步骤称为原始特征获取. 然而, 这些原始特征一般都存在信息冗余, 维数过高, 区分性不够等问题. 为了能够更有效地表征输入人脸表情的本质, 需要对原始特征数据需要较好的预处理方法, 因此使用PCA进行降维. 主要提取的方式如图2所示.

|
图 2 人脸特征点提取过程 |
PCA是一种分析、简化数据集的技术. 主成分分析经常用于减少数据集维数, 同时保持数据集中对方差贡献最大的特征.
利用PCA进行特征值降维的基本原理如下:
对于一个M×N的矩阵, 其中M为样本数, 每个样本包含N个特征(n维).
1) 进行样本矩阵中心化, 每一维的数据都减去该维的均值, 将每一维的均值变为0.
即对于第m个样本, 第n个特征值, 将该值代入式(1)进行运算.
| ${{X}}[m,n] = {{X}}[m,n] - \frac{1}{M}\sum\limits_{m = 1}^M {{{X}}[} m,n]$ | (1) |
2) 计算样本特征的协方差矩阵
协方差矩阵的第
| ${\rm{cov}}\left( {{{{X}}_i},{{{X}}_j}} \right) = {\rm{E}}[\left( {{{{X}}_i} - {u_i}} \right)\left( {{{{X}}_j} - {u_j}{)^{\rm{T}}}} \right]$ | (2) |
则协方差矩阵如式(3)所示[10].
| ${{C}} = {\rm{E}}\left[ {\left( {{{X}} - {\rm{E}}\left[ {{X}} \right]} \right){{\left( {{X} - {\rm{E}}\left[ {{X}} \right]} \right)}^{\rm{T}}}} \right] = \frac{1}{N}{{X}} \bullet {{{X}}^{\rm{T}}}$ | (3) |
矩阵中第
2) 计算协方差矩阵的特征值和特征向量
得到N个特征值与N个特征向量. 将N个特征向量根据其对应的特征值从大到小进行排列, 取其中前k列, 组成一个N×k的降维矩阵[11].
3) 降维计算
将原M×N矩阵与上述步骤得到的降维矩阵N×k相乘, 便得到结果, 一个M×k的矩阵. 其中M为样本数量, k为其维度.
4) 应用
应用到人脸图像的特征值处理, 将原始特征作为初始的输入维度, 进行人脸特征值降维处理, 减少接下来表情识别的计算量.
2.4 人脸表情识别方法在表情识别方面, 采用基于卷积神经网络的方法.
卷积神经网络的训练方法总体上与传统神经网络类似, 但是由于其特殊结构, 不同的层在误差回传、前向激活时有所不同, 其具体步骤如下[12]:
1) 前向传导阶段
从样本集中选取一个样本
| ${\rm{g}}\left( {{w_i}*{a_i}} \right) = {a_{i + 1}}$ | (4) |
其中, wi表示第i层各个神经元的权重, ai表示第i层各个神经元输入, ai+1表示第i层各个神经元输出. 这个输出将作为第i+1层神经元的输入, 迭代直到输出层.
2) 反向传播阶段
定义代价函数Loss如式(5)所示.
| $Loss = - \frac{1}{m}\mathop \sum \limits_{i = 1}^m {y_i}{\rm{log}}f\left( {{x_i}} \right) + \lambda \mathop \sum \limits_{k = 1}^l{\rm{ sum}}\left( {w_k^2} \right)$ | (5) |
其中m为样本集中样本的个数, l为卷积神经网络的层数.
网络参数更新需要计算网络参数残差, 其中包括输出层残差, 下一层为池采样层(pooling层)的卷积层的残差以及下一层为卷积层的pooling层的残差.
在反向传播阶段里, 需要将损失函数产生的残差依层次往前传递, 在传递的过程中, 全连接层、pooling层、卷积层的残差计算方法和更新权值矩阵的计算方法不同, 如下为具体几种情况的计算方式和步骤.
1) 计算输出层的残差
针对单个样本
| $Loss = l\left( {f\left( x \right),y} \right) = - \mathop \sum \limits_c {l_{\left( {y = c} \right)}}{\rm{log}}f{\left( x \right)_c} = - {\rm{log}}f{\left( x \right)_y}$ | (6) |
其中下标c的含义如式(7)所示.
| $f{(x)_c} = p(y = c|x)$ | (7) |
由此可得如式(8)所示此时Loss值相对于输出层的残差.
| $\frac{\partial }{{\partial {\alpha ^{\left( {L + 1} \right)}}{{\left( x \right)}_c}}}\left( { - {\rm{log}}f{{\left( x \right)}_y}} \right) = - \left( {e\left( y \right) - f\left( x \right)} \right)$ | (8) |
式中
式(9)为第L层的权值Wl的偏导数.
| $\frac{{\partial Loss}}{{\partial {W_L}}} = - \frac{1}{m}\left( {e\left( y \right) - f\left( x \right)} \right)*f{\left( x \right)'} + \lambda {W_L}$ | (9) |
式(10)为输出层偏置的偏导数.
| $\frac{{\partial Loss}}{{\partial {b_l}}} = - \frac{1}{m}\left( {e\left( y \right) - f\left( x \right)} \right)$ | (10) |
其中
2) 下一层是pooling层的卷积层的残差值
假设第一层为卷积层, 第l+1层为pooling层, 且pooling层的残差如式(11)所示.
| ${\rm{\delta }}_J^l = upsample\left( {{\rm{\delta }}_J^{l + 1}} \right) \bullet h{\left( {a_J^l} \right)'}$ | (11) |
其中•表示矩阵的点乘操作, 卷积层和unsample后的pooling层节点是一一对应的, 所以下标都用j表示, 符号
3) 再下一层是卷积层的pooling层残差计算
假设pooling层(第l层)有 N个通道, 即有N张特征图, 卷积层(l+1层)有M个特征, l+1层中每个通道图都对应有自己的残差项, 则式(12)为第l+1层第j个通道的残差计算方法.
| $\frac{{\partial Loss}}{{\partial {k_{ij}}}} = x_i^l \otimes \delta _J^{l + 1}$ | (12) |
其中, 符号
4) 卷积层相连接层的权值、偏置值的导数计算
第l层第i个通道与第l+1层第j个通道之间的权值和偏置的导数计算方法如式(13)所示.
| $\frac{{\partial Loss}}{{\partial {b_l}}} = \mathop \sum \limits_{u,v} {\left( {{\rm{\delta }}_J^{l + 1}} \right)_{u,v}}$ | (13) |
对于训练完的分类器, 将上文利用PCA提取到的特征值, 将其作为输入输进神经网络的输入层, 如上述前向传导的过程, 迭代直到输出层, 输出表情结果.
3 脑电信息处理的基本原理和实现 3.1 脑电信息处理流程通过Neurosky公司的脑电设备, 即时提取脑电波的特征值, 当接收到识别的命令, 将当前的值先做特征处理, 再作为输入传入SVM分类器, 得出结果. 详细过程见图3.

|
图 3 脑电处理流程 |
3.2 脑电特征值的预处理和特征分类
使用Neurosky公司的脑电提取设备, 提取出来每种的脑电波的值是一个无符号整数. 特征预处理采用的方法是特征标准化和归一化, 再使用训练好的SVM分类器进行特征的分类, 将特征分为虚弱、普通、强烈三类, 分别对应情绪的不同状态.
3.3 利用SVM算法进行脑电特征值训练的基本原理对于给定训练样本:
| $D = \left\{ {\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right), \cdots ,\left( {{x_m},{y_m}} \right)} \right\}$ |
分类学习最基本思想就是基于训练集D在样本空间找到一个划分超平面, 使得不同类别的样本分开[13].
设线性可分时存在超平面可表示为式(14):
| $f\left( x \right) = {{w}^{\rm{T}}}x + b$ | (14) |
其中, w为待确定的行向量. 则每个样本点到超平面的距离r如式(15)所示.
| $r = \frac{{\left| {{{w}^{\rm{T}}} + b} \right|}}{{w}}$ | (15) |
若
若
令
| $\left\{ {\begin{array}{*{20}{c}}{{{w}^{\rm{T}}}x + b \ge + 1}\\{{{w}^{\rm{T}}}x + b \le - 1}\end{array}} \right.$ | (16) |
距离超平面最近的训练样本点使得上式等号成立, 他们被称为“支持向量”. 支持向量的点到超平面的距离之和如式(17)所示.
| $r = \frac{2}{{w}}$ | (17) |
因此要求出超平面, 就是求出满足式(18)的w值.
| $\mathop {\max }\limits_{{w},b} \frac{2}{{w}},\;\;{\rm{s.t.}}\;\;{y_i}({{w}^{\rm{T}}}x + b) \ge 1,\;\; i = 1,2, \cdots ,m$ | (18) |
为了简化计算, 等价于计算式(19).
| $\mathop {\min }\limits_{{w},b} \frac{{{{w}^2}}}{2},\;\;{\rm{s.t.}}\;\;{y_i}({{w}^{\rm{T}}}x + b) \ge 1,\;\;i = 1,2, \cdots ,m$ | (19) |
式(19)是一个二次规划问题, 可用拉格朗日乘子法求得最优解.
线性不可分时存在超平面可将样本从原始空间映射到一个更高维的特征空间, 使得样本在整个样本空间线性可分.
令
| $f\left( x \right) = {{w}^{\rm{T}}}g\left( x \right) + b$ | (20) |
求解w过程类似于上述线性可分情况.
对于多分类问题, 将多分类任务拆解为若干个二分类任务求解.
应用到脑电波训练问题, 对于每个样本点
| $\begin{array}{l}{x_i} = \left[ \begin{array}{l}DELTA,THETA,ALPHA1,ALPHA2,\\BETA1,BETA2,GAMMA1,GAMMA2\end{array} \right]\\{y_i} = \left\{ {\begin{array}{*{20}{c}}{ - 1\quad\small\text{虚弱}}\\{0\quad\small\text{普通}}\\{ + 1\quad\small\text{强烈}}\end{array}} \right.\end{array}$ | (21) |
求解一个w, 使得存在
| $f\left( x \right) = {{w}^{\rm{T}}}x + b$ | (22) |
使得样本分为两类(先把–1和0看成一类, 1看成另一类). 若找不到存在的w满足条件, 则通过核函数向高维映射. 然后再通过分成多类的方法(区分–1和0类), 将其分为三类.
4 信息融合的基本原理和实现 4.1 信息融合主要流程
|
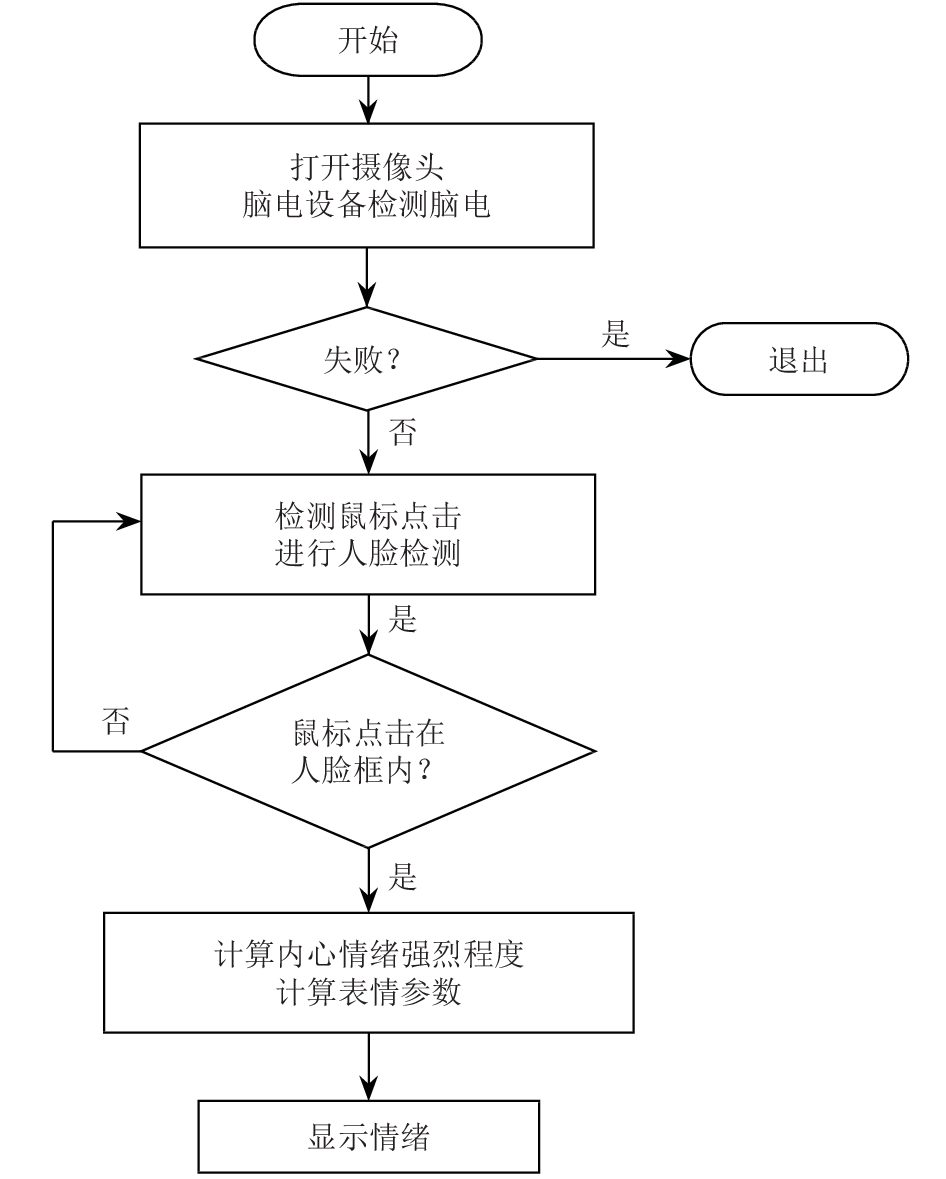
图 4 信息融合主要流程图 |
如图4所示, 首先利用设备摄像头检测当前画面图像, 利用所训练的Haar分类器, 找出人脸位置, 框出来. 与此同时, 脑电设备每隔1 s检测人脑电波, 不断更新.
当系统接收到要进行情绪识别的信号(即鼠标点击人脸框). 人脸图像模块进行人脸特征提取和表情计算返回当前人脸表情. 脑电处理模块进行特征预处理和特征分类返回当前人内心情绪的波动程度. 信息融合模块汇总上述2个模块的信息, 给出最终结果, 判断出人的真正情绪.
5 实验和结果下面三种实验分别分为在线和离线实验, 在线实验用来产生训练数据, 离线实验的数据用来测试本文方法的准确率.
每次实验开始, 首先在大屏幕的中心呈现固定十字, 以吸引实验对象的注意力, 2秒后, 对应不同情绪的片段出现在屏幕中心. 每个片段2~3分钟, 片段之间间隔10秒让实验对象恢复情绪. 情绪的得分使用Manikin自我评定表获取[14].
实验中采用摄像头(25FPS, 800×600图像大小)获取人脸图像. 采用脑电设备(Neurosky, Inc., Abbotsford, Australia)获取脑电, 从“Fz”电极获取用于分析的脑电信号. 所有电极的电阻保持在5 kΩ以下.
实验数据在Windows下采用python3.5进行处理. 图像方面算法用谷歌的开源深度学习框架tensorflow. 脑电方面算法用python开源库scikit-learn. 信息融合算法自己用python实现.
5.1 表情识别效果表情识别实验对象为20个18~22岁的青年, 男女比例1:1. 每个对象检测八种基本表情, 每种表情检测3次. 检测环境有在光照强度大的环境, 也有在光照较差的环境. 被测人的内心状态各有不同, 但都被要求做出所需要的表情.
表情识别实验效果准确率如图5表示, 其中, x轴表示实验者编号, y轴表示准确率.

|
图 5 人脸表情检测准确率 |
表情识别实验效果显示, 虽然对人脸表情检测准确率能够高达81.35%, 但是对内心情绪波动程度的辨别程度几乎为0. 单纯基于人脸图像对真实情绪检测的准确率并不高, 其曲线如图9 (三种情绪识别效果对比可以体现出来).
5.2 脑电信息进行情绪强弱程度分析效果以上进行表情检测的20个人, 只利用脑电设备, 在其内心情绪的不同状态, 检测10次, 每人每次作为一个样本. 进行内心情绪波动程度的检测. 检测的效果如表1.
| 表 1 脑电情绪强弱程度分析效果 |
可以看到, 利用脑电信息对内心情绪波动检测的方法对内心情绪波动微弱检测的召回率较差, 但在其他方面均可达到0.8左右的效果.
5.3 表情识别与脑电信息进行信息融合的效果用相同的20个人, 在表情识别实验基础上, 加入利用脑电信息进行情绪波动分析的方法进行检测. 很大程度上弥补了表情识别无法识别出内心情绪波动的缺陷.

|
图 6 情绪强烈的效果图 |

|
图 7 正常情绪效果图 |
|
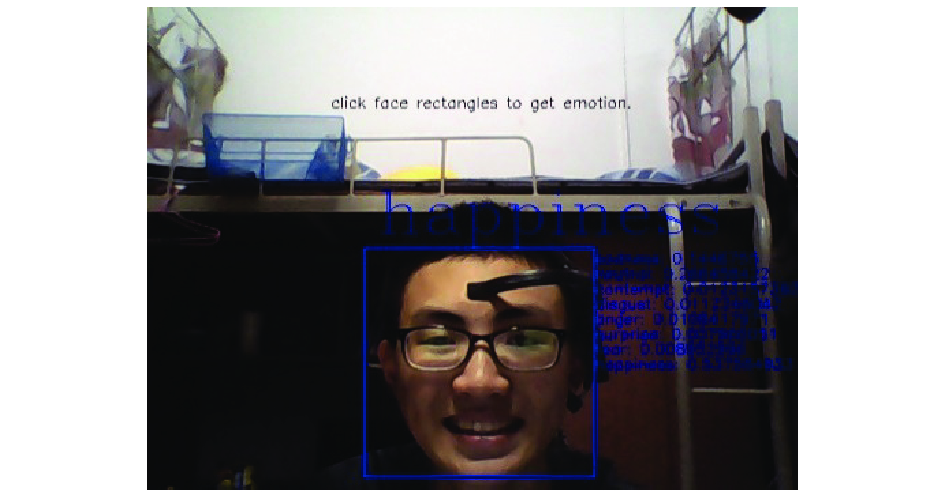
图 8 微弱情绪效果图 |
开心情绪的识别效果如图6, 7, 8所示, 被实验人都被要求做出微笑表情. 图6是在被实验人听欢快音乐1分钟后所试验, 图8是在被实验人听悲伤音乐1分钟后所试验, 图7是在被实验人情绪波动正常时试验.
三种情绪识别的效果图如图9所示, 其中,x轴表示实验者编号, y轴表示准确率.

|
图 9 三种情绪识别的效果图 |
可以看到, 只基于面部表情进行真实情绪识别有较高的波动性, 这是因为只要被实验人懂得假装自己的面部表情就可以成功地“骗”过机器. 利用人脸表情和脑电信息进行情绪识别很好地弥补了只基于单一信息源识别信息单一的缺陷. 在检测出面部表情的基础上, 还检测出了内心情绪的波动程度, 这部分的准确率在71.53%. 很大程度上拓宽了情绪信息的广度.
6 总结本文利用信息融合技术结合人脸表情识别技术与脑电情绪识别技术. 不仅检测出了情绪的分类, 还检测出了情绪的强弱程度. 对比其他文献的实验结果, 他们大多只检测了情绪的分类, 对于情绪的强弱程度这方面, 目前并没有太多的研究者去做. 比如说, Murugappan等人从脑电信号中提取多解析度的小波变换作为特征, 对高兴、厌恶、恐惧三种情绪进行了聚类[5]. Li等人指出Gamma频带的脑电信号对于愉悦和悲伤两种情绪的分类有很高的解析度[15].
这些实验大多只检测出了情绪的种类, 而且检测出情绪的种类并不够多. 而利用信息融合的方法, 不仅可以检测出情绪的种类, 而且还可以检测出情绪的强弱程度. 说明利用信息融合的方法更适合用于情绪识别. 下一步的工作: 由于内心情绪的不可控性, 导致进行内心情绪的检测过程困难, 难以得到高质量的脑电数据. 这进一步导致了脑电部分的估测准确率不高. 但是一旦有高质量的脑电数据, 进行分类器的重新训练, 就可以大大提高基于脑电信息的内心情绪识别的准确率.
| [1] |
Ekman P, Friesen WV. Facial action coding system: A technique for the measurement of facial movement. Palo Alto: Consulting Psychologists Press, 1978.
|
| [2] |
Shao H, Chen S, Zhao JY, et al. Face recognition based on subset selection via metric learning on manifold. Frontiers of Information Technology & Electronic Engineering, 2015, 16(12): 1046-1058. |
| [3] |
Hu XP, Wang Y, Zhu FY, et al. Learning-based fully 3D face reconstruction from a single image. Proceedings of 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Shanghai, China. 2016. 1651–1655.
|
| [4] |
王志良, 陈锋军, 薛为民. 人脸表情识别方法综述. 计算机应用与软件, 2003, 20(12): 63-66. DOI:10.3969/j.issn.1000-386X.2003.12.027 |
| [5] |
Murugappan M, Rizon M, Nagarajan R, et al. EEG feature extraction for classifying emotions using FCM and FKM. International Journal of Computers and Communications, 2007, 2(1): 21-25. |
| [6] |
Bos DO. EEG-based emotion recognition. The Influence of Visual and Auditory Stimuli, 2006.
|
| [7] |
Yazdani A, Lee JS, Ebrahimi T. Implicit emotional tagging of multimedia using EEG signals and brain computer interface. Proceedings of the First SIGMM Workshop on Social Media. Beijing, China. 2009. 81–88.
|
| [8] |
Petrantonakis PC, Hadjileontiadis LJ. Emotion recognition from EEG using higher order crossings. IEEE Transactions on Information Technology in Biomedicine, 2010, 14(2): 186-197. DOI:10.1109/TITB.2009.2034649 |
| [9] |
江伟坚, 郭躬德, 赖智铭. 基于新Haar-like特征的Adaboost人脸检测算法. 山东大学学报(工学版), 2014, 44(2): 43-48. DOI:10.6040/j.issn.1672-3961.1.2013.003 |
| [10] |
曾阳艳, 叶柏龙. 基于PCA方法的人脸特征提取和检测. 电脑知识与技术, 2008, 1(4): 742-744. |
| [11] |
高绪伟. 核PCA特征提取方法及其应用研究[硕士学位论文]. 南京: 南京航空航天大学, 2009.
|
| [12] |
王剑云. 基于深度神经网络的表情识别算法[硕士学位论文]. 绵阳: 西南科技大学, 2015.
|
| [13] |
张国云. 支持向量机算法及其应用研究[博士学位论文]. 长沙: 湖南大学, 2006.
|
| [14] |
Bradley MM, Lang PJ. Measuring emotion: The self-assessment Manikin and the semantic differential. Journal of Behavior Therapy and Experimental Psychiatry, 1994, 25(1): 49-59. DOI:10.1016/0005-7916(94)90063-9 |
| [15] |
Li M, Lu BL. Emotion classification based on gamma-band EEG. Proceedings of 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Minneapolis, MN, USA. 2009. 1223–1226.
|
 2018, Vol. 27
2018, Vol. 27



