我国股票市场是一个年轻且成长迅猛的市场. 据统计, 到2016年4月底, 上交所股票个数高达1140只, 股票市价总值高达249 670.56亿元, 中国股市已经成为中国金融体系中越来越重要的一份子. 中国股市在飞速发展的过程中伴随着多样的波动性特征, 对股票的统计特征规律进行全面的挖掘研究为风险管理及投资管理提供了坚实的理论基础.
国外对股票波动规律的研究起步较早, 目前已有的经典理论有如: 投资组合理论、资本资产定价模型、有效市场理论、期权定价模型等. 但上述经典理论中, 学者们通常认为股票收益率是一个服从高斯分布, 且标准差为某常数的独立序列. 然而20世纪60年代后, 有学者提出股票收益率不服从正态分布, 却具有“尖峰厚尾”的特征[1]. 于是, 国外学者开始考虑不同时间范围、股票指数、个股市值下的股票收益率不同的分布特征. 如Drożdż等[2](2007)收集了S&P、DAX和WIG200股票市场从2004年至2006年的股票收益率, 并将时间刻度从高频的4 min逐渐调整到120 min, 发现标准化后的股票收益的累计分布大致从q-正态分布. Lillo等[3](2000)研究了纽约交易市场中个股流通市值对个股的收益率分布特征的影响, 发现流通市值越高, 股票收益率越收敛于正态分布. 另外, 国外学者们也开始利用各种模型针对股票的聚类性、持续性以及“肥尾”的特点对收益率进行拟合, 如Yanhui Xi等[4] (2015)通过建立基于学生t分布的市场微观模型来拟合金融时间序列, 并发现这种模型优于带学生t分布的SV-t模型. Horváth等[5](2016)采用带有学生t分布和正态分布的GARCH模型对S&P 500股票市场的尾部进行了估计. 国内方面, 较早的有陶亚民, 蔡明超等[6] (1999)通过非参数的拟合检验和收益率的统计参数考察上海股票市场的收益率, 发现股票收益率不服从正态分布, 而且与股票持有期有关. 后来王志诚、邓召明[7] (2001)采用沪深A股1995年至2000年的市场交易数据, 研究了每只股票和每个时间这两个截面的数据, 并发现收益计算周期的延长, 会导致资产收益的峰度逐渐消失. 近年来, 国内学者主要采用GARCH族模型和SV模型对收益率进行拟合, 如刘玄和冯彩[8] (2009)、吴鑫育等[9](2014). 纵观国内外文献, 我们可以发现国内外学者大多利用某固定的时间范围和时间刻度的股票数据, 并通常选择某股票指数如上证指数、沪深300指来研究股市的总体变化. 然而这不仅不能灵活调控时间范围和时间刻度, 而且没有很好地反映个股之间具体属性的差异(如流通市值和所属行业)对股票收益率带来的影响. 因此, 本文旨在研究多时间范围、多时间刻度下的单只股票或不同股票行业的收益率统计特征, 而如果手工搜集不同范围的股票数据且利用相同方法进行研究, 这无疑工作量巨大且效率低下. 为此, 本文基于上证A股的每日、周、月行情数据建立数据库系统, 同时建立Matlab GUI界面以便于查询相应数据和挖掘研究.
本篇论文的结构如下. 第1部分介绍了数据选取及建立的数据库系统. 第2部分的研究对象是单只股票截面下的收益率, 探究了收益率的概率密度分布特征受个股流通市值的影响, 结果表明个股的流通市值越大, 收益率的概率密度分布越为尖峰. 同时, 本文还通过改变研究的时间刻度和股票行业类别来分析分布特征的变化情况. 第3部分的研究对象是单位时间截面下股票集合的收益率, 并讨论了收益率的统计特征, 包括均值的概率密度分布、股票之间与时间之间的相关性、波动率及其自相关性. 最后为结论.
1 数据选取及数据库建立 1.1 数据选取本文选取上证A股(共765只)的历史行情数据, 时间刻度是日/周/月, 时间范围为2006年1月4日到2015年12月31日共10年, 除去周末及节假日, 共有2429个交易日, 513周, 120个月. 经统计, 日股票综合数据量约为175万, 周股票综合数据量约为36.2万, 月股票综合数据量约为8.5万.
股票数据具体介绍: 本文中的日/周/月股票数据来自于RESSET金融研究数据库. 由于上交所成立时间为1990年12月19日, 因此选择上市日期在1990年12月19日至2005年12月31日, 当前状态为“正常上市”的所有A股股票, 共765只. 因此对于这个上市时间区间内的所有股票都拥有完整的近十年数据. 此时, 对于所选择的上市日期区间内的股票, 当前状态共有5种可能: 正常上市、ST、*ST、暂停上市、退市及三板市场, 本文只选择正常上市的股票.
1.2 数据库建立利用股票的收盘价数据, 本文首先根据公式(1)计算股票收益率Ri(t), 然后将股票收益率数据存入数据库SQL SERVER中.
| ${R_i}\left( t \right) = \frac{{{Y_i}\left( t \right) - {Y_i}\left( {t - \tau } \right)}}{{{Y_i}\left( {t - \tau } \right)}}$ | (1) |
上式中, i=1, 2, 3,…, n; τ=1日/周/月; Yi(t)是单位时间t下第i只股票的收盘价. Ri(t)则代表第i只股票t时刻下的股票收益率.
建立股票收益率数据库后, 将Matlab通过ODBC与数据库连接, 达到在Matlab GUI端调控时间范围、时间刻度和股票行业的目的, 进而灵活地挖掘多个时间子区域、多种时间刻度以及不同股票行业下股票收益率的统计特征.
2 单只股票截面统计特征 2.1 研究方法不同上市公司具有不同的公司规模, 本文用流通市值代表公司规模. 为了研究公司规模、时间刻度以及股票行业对股票收益率分布特征的影响, 下面具体按照五个步骤进行研究:
步骤1. 对每只股票的收益率按公式
| ${\mu _i} = \frac{1}{{{T_i}}}\sum\limits_{t = 1}^{{T_i}} {{R_i}(t)} $ | (2) |
| ${\sigma _i} = \sqrt {\frac{1}{{{T_i}}}(\sum\limits_{t = 1}^{{T_i}} {{{({R_i}(t) - {\mu _i})}^2})} } $ | (3) |
步骤2. 按2015年12月31日的流通市值大小对所选股票由大到小排序, 并重新编号.
步骤3. 按流通市值大小顺序同步绘制单只股票收益率的概率密度分布图, 其反映在坐标系中是以股票的经验概率密度分布曲线为X-Z面, 以个股流通市值排序后的序号为Y轴的三维图, 从而在三维图中可直观判断单只股票收益率分布的形状及其与流通市值的关系. 其中,Z轴采用自然对数坐标.
步骤4. 步骤3是通过直接观察分布图定性地概括分布特征与流通市值的关系. 而为了更定量地得出结论, 在此采用Lillo[3]文中检验正态分布的方法, 度量单只股票收益率的经验概率密度分布与正态分布的差距, 并分析这种差距与流通市值的关系.
下面是具体的检验正态分布的量化方法, 即1)-3):
1) 对每一组数据按照公式(4)计算h值. 公式中,
| $h \equiv \frac{{\left\langle {\left. {\left| x \right|} \right\rangle } \right.}}{{\sqrt {\left\langle {\left. {{x^2}} \right\rangle } \right. - {{\left\langle {\left. x \right\rangle } \right.}^2}} }}$ | (4) |
2) 利用正态分布的函数表达式得出hG的计算公式, 见公式(5):
| ${h_G} = \sqrt {\frac{2}{\pi }} \left[ {\exp \left( { - \frac{{{\mu ^2}_G}}{{2{\sigma ^2}_G}}} \right) + \sqrt {\frac{\pi }{2}} \frac{{{\mu _G}}}{{{\sigma _G}}}Erf\left( {\frac{{{\mu _G}}}{{\sqrt 2 {\sigma _G}}}} \right)} \right]$ | (5) |
由公式(5)可知参数hG是比率μG/σG的函数, 取值范围从最低的
3) 比较h和hG的距离, 来量化经验概率密度分布正态分布的差距. 与此同时, 本文通过绘制个股h值随流通市值变化的散点图反映收益率分布特征与流通市值的关系.
步骤5. 改变所研究股票的行业类别和时间刻度, 按公式(4)计算相应的h值, 对比分析后得出更多结论.
2.2 实证研究与分析由于文章篇幅限制, 本节只改变时间刻度和股票行业的取值, 而时间范围则均为全部十年. 因此分为三块进行挖掘研究: (1) 时间刻度为日, 股票行业为全部行业; (2) 时间刻度为月和周, 其他不变; (3) 股票行业为各个子行业, 其他不变.
(1) 时间刻度为日, 股票行业为全部行业.
|
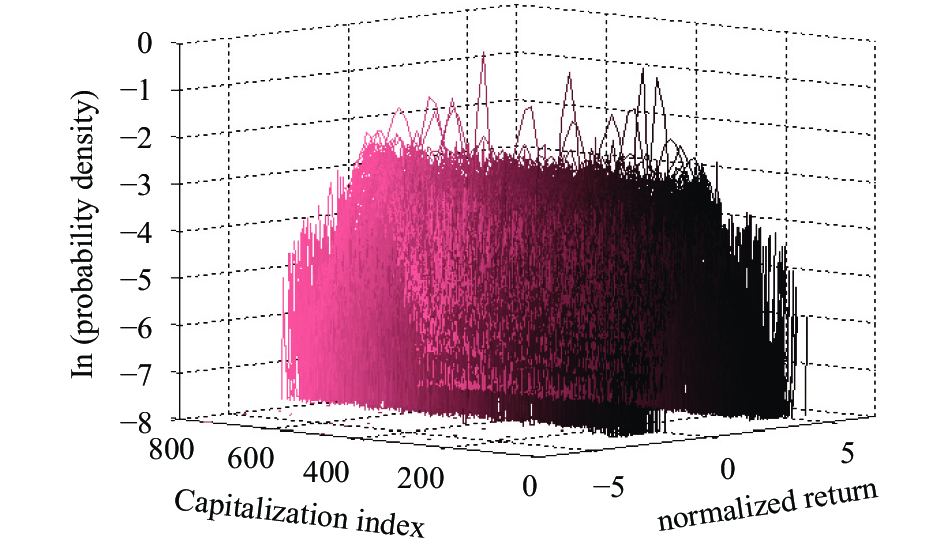
图 1 由每只股票收益率的概率密度分布与其流通市值绘制而成的三维图 |
|
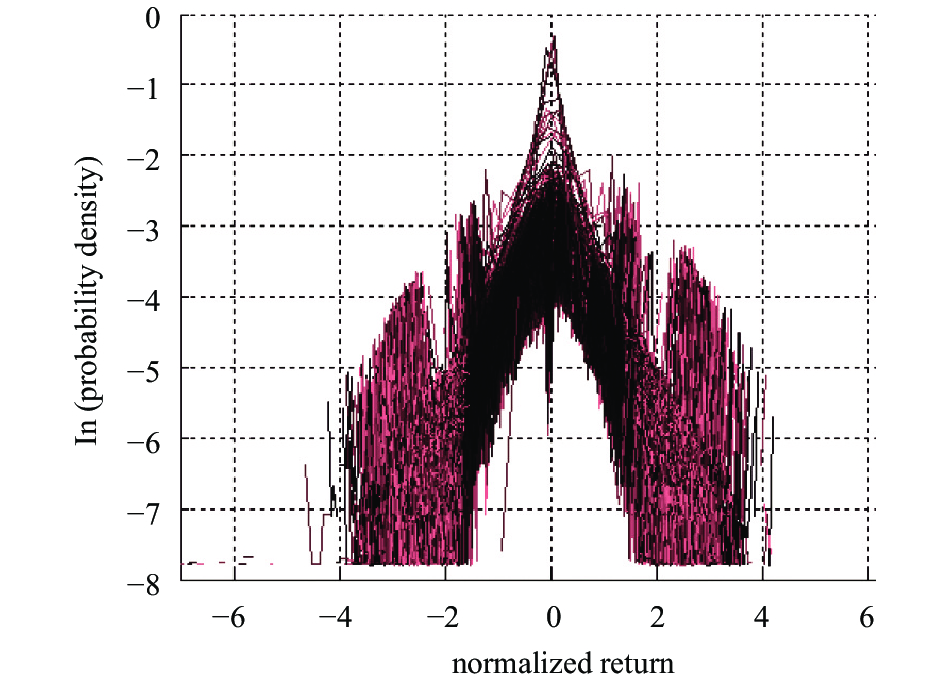
图 2 图1的X-Z视图 |
图1展示了每只股票收益率的经验概率密度分布, 按个股流通市值的大小依次排列形成的三维图. 由图1我们可以观察到每只股票的形状大多数都是相似的, 为铃铛形状, 只有个别股票更加尖峰. 但由于曲线较为密集, 我们很难看出不同股票的分布特征与其流通市值的关系, 因此下面对图1的X-Z视图(图2)进一步分析.
为便于观察, 在仿真中, 本文将不同流通市值的股票用深浅不同的颜色表示, 即流通市值越大, 颜色越浅. 图2表示所有股票的收益率概率密度分布的X-Z视图. 从图2中我们可以观察到图形的中部颜色较深, 因此, 流通市值高的股票的密度分布比流通市值少的股票的密度分布更具高狭峰.
2) 由步骤4, 系统可以得出图3.

|
图 3 正态分布检验图 |
图3中每个点的纵坐标表示单只股票收益率分布的h值, 横坐标表示该股票流通市值的常用对数值. 最上方的虚线表示
由图3我们可以观察到基本上所有股票都满足h<hG; 且经计算, 日时间刻度下的h值hd的平均值为0.6954, 这表明个股收益率的经验概率密度分布是尖峰分布. 另外, 从散点图的整体走势来看, h随流通市值的增加而缓慢减小. 因此, 流通市值较大的股票比较小流通市值的股票具有一个峰值更高的收益概率密度分布.
(2) 时间刻度为月和周, 其他不变.
为研究收益率的分布规律与时间刻度的关系, 下面按公式(4)计算时间刻度为周和月的h值: hm和hw, 它们的均值分别是: 0.7023和0.7108. 对比hd、hw和hm的均值可知: 当时间刻度增加时, h值向
(3) 股票行业为各个子行业, 其他不变.
股票行业种类不同, 相应的分布特征亦不同. 对该规律的探索可以加强投资者对行业动态的关注. 本文采用的股票行业分类标准是证监会行业分类2012版, 共19个一类分类.
表1即为不同股票行业种类的h值由大到小排序后的结果. 居民服务、修理和其他服务业种类的股票数量为0, 未列入表中.
| 表 1 不同行业的h值 |
对比表1中各行业的h值, 我们可以发现金融业的h值最低, 约为0.6550; 科学研究和技术服务业的h值最高, 约为0.7740. 经计算, h均值为0.69989, 而制造业与h均值的差值最小, 因此, 制造业反映了所有股票行业分布特征的一个平均状况, 投资者需要更加关注制造业的发展动态.
3 时间截面下股票集合的统计特征第3部分研究的是单只股票截面下股票收益率的统计特征, 而对每个交易日来讲, 所有股票形成一个股票集合. 此部分则研究单位时间股票集合的统计特征, 包括均值的概率密度分布、股票两两之间与时间两两之间的相关性、波动率及其自相关性(本节均利用日股票收益率数据).
3.1 股票集合的收益率均值 3.1.1 均值的概率密度分布为研究2013.01-2015.12这三年所有股票的收益率均值的分布特征, 系统首先利用公式(2)和公式(6)分别计算相应时间范围内的μ(t)和μi, 即每日股票集合的收益率均值和每只股票的收益率均值, 然后分别绘制两个变量的概率密度分布图, 最后可得出图4.
| $\mu \left( t \right) = \frac{1}{{{n_t}}}\sum\limits_{i = 1}^{{n_t}} {{R_i}\left( t \right)} $ | (6) |
图4采用对数-对数坐标系, 图(a)表示μ(t)的密度分布, 图(b)表示μi的密度分布. 直观来看, 变量μ(t)和μi的统计特征明显不同: μ(t)的概率密度分布图像比μi的更宽, 具体原因将在3.1.2中讨论.

|
图 4 μ(t)和μi的概率密度分布对比图 |
3.1.2 股票之间与时间序列之间的相关性
为探究μ(t)和μi的概率密度分布特征不同的原因, 下面先假设市场中共T个交易日, N只股票. 那么, 我们可得到公式(7).
| ${\left\langle {\left. {{\mu _i}} \right\rangle } \right._i} = {\left\langle {\left. {\mu \left( t \right)} \right\rangle } \right._t} \equiv \mu $ | (7) |
其中,
虽然μi和μ(t)的均值相同, 但它们的方差一般是不相同的. 接下来按公式(8)表示μ(t)的方差, 公式(10)表示μi的方差.
| $Var\left[ {\mu \left( t \right)} \right] \equiv \frac{1}{T}{\sum\limits_{t = 1}^T {\left[ {\mu \left( t \right) - \mu } \right]} ^2} = \frac{1}{{{N^2}}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\sigma ^2}_{ij}} } $ | (8) |
其中,
| ${\sigma ^2}_{ij} = \left\langle {{{\left. {{R_i}\left( t \right){R_j}\left( t \right)} \right\rangle }_t}} \right. - \left\langle {{{\left. {{R_i}\left( t \right)} \right\rangle }_t}} \right.{\left\langle {\left. {{R_j}\left( t \right)} \right\rangle } \right._t}$ | (9) |
| $Var\left[ {{\mu _i}} \right] \equiv \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{\mu _i} - \mu } \right)}^2}} = \frac{1}{{{T^2}}}\sum\limits_{t = 1}^T {\sum\limits_{t' = 1}^T {{\sigma ^2}_{tt'}} } $ | (10) |
其中,
| ${\sigma ^2}_{tt'} = \left\langle {{{\left. {{R_i}\left( t \right){R_i}\left( {t'} \right)} \right\rangle }_i}} \right. - \left\langle {{{\left. {{R_i}\left( t \right)} \right\rangle }_i}} \right.\left\langle {{{\left. {{R_i}\left( {t'} \right)} \right\rangle }_i}} \right.$ | (11) |
经推导后得到公式(12)[3]:
| $Var\left[ {\mu \left( t \right)} \right] - Var\left[ {{\mu _i}} \right] \cong \left\langle {{{\left. {{\sigma ^2}_{ij}} \right\rangle }_{i \ne j}}} \right. - \left\langle {{{\left. {{\sigma ^2}_{tt'}} \right\rangle }_{t \ne t'}}} \right.$ | (12) |
因此, 相关强度的大小则可以转化为两个均值的方差大小. 从图4中我们可以发现
本文通过计算单位时间股票集合的收益率标准差σ(t), 来测定股票集合的波动性, 见公式(13).
| $\sigma \left( t \right) = \sqrt {\frac{1}{{{n_t}}}\left( {\sum\limits_{i = 1}^{{n_t}} {{{\left[ {{R_i}\left( t \right) - \mu \left( t \right)} \right]}^2}} } \right)} $ | (13) |
其中, nt代表单位时间t下的股票总数. 标准差σ(t)是股票集合收益率密度分布的宽度, 它反映了单位时间下不同公司收益率的差距. 因此, 标准差也被称为股票的波动率.
3.2.2 波动率的自相关性关于波动率的一个重要的统计特征是它们的自相关性. 为研究波动率σ(t)关于自身的相关性, 本文利用公式(14)所示的自相关函数:
| $R(\tau) \equiv \frac{\langle {x(t)x(t+\tau)} \rangle - \langle {x(t)} \rangle \langle x(t+\tau) \rangle }{\langle {x( t)^2} \rangle - \langle x(t) \rangle ^2}$ | (14) |
在公式(14)中, 设置τ的最大值为100日, 通过改变时间间距τ的大小(从1逐一变化到100), 可以计算出标准差σ(t)的一组的自相关函数值, 共100个; 然后系统对得出的自相关函数值进行幂律函数(见公式(15))拟合, 得到具体的函数表达式. 具体拟合结果见图5.
| $R(\tau ) \propto {\tau ^{ - \delta }}$ | (15) |
由图5可知波动率σ(t)的自相关函数服从幂律分布, 得到拟合系数–7.006, 即δ=7.006, 并且拟合误差很小, 这表明变量σ(t)在市场中具有长期记忆性.

|
图 5 自相关函数值的幂律函数拟合图 |
4 结语
本文从单只股票截面和单位时间截面的两个角度出发, 建立股票收益率挖掘系统对上证A股近十年的收益率数据进行挖掘. 在系统上适当改变时间范围、股票行业和时间刻度的基础上, 本文得出以下结论: (1)个股收益率的分布特征与其流通市值确实有关系, 从整体趋势上来看, 流通市值越大, 收益率的概率密度分布越尖峰. (2)当股票收益率的时间刻度由小到大发生变化时, h会变大, 即收益率更加收敛于正态分布. (3)股票收益率的分布特征与行业种类密切相关, 金融业更加尖峰, 而制造业则反映了所有行业的平均水平. (4)时间截面上股票集合收益率均值的概率密度分布的宽度明显大于个股收益率均值的相应宽度, 这是因为股票两两之间的相关性强度远大于时间之间的相关性. (5)股票波动率的自相关函数符合幂律函数, 这说明股票波动率具有长期记忆性.
本文为挖掘股票收益率的统计特征提供了简便灵活的仿真过程. 如今股市发展迅速, 数据亦爆发式增长, 而通过对股市数据的统计特征的观察可以让人们更加清楚金融市场更本质的运行特征和规律. 因此如何处理好股票大数据与适合中国国情的多种统计模型之间的快捷交互是未来的研究重点.
| [1] |
Mandelbrot B. The variation of certain speculative prices. The Journal of Business, 1963, 36(4): 394-419. DOI:10.1086/jb.1963.36.issue-4 |
| [2] |
Drożdż S, Forczek M, Kwapień J, et al. Stock market return distributions: From past to present. Physica A: Statistical Mechanics and Its Applications, 2007, 383(1): 59-64. DOI:10.1016/j.physa.2007.04.130 |
| [3] |
Lillo F, Mantegna RN. Variety and volatility in financial markets. Physical Review. E, Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 2000, 62: 6126-6134. |
| [4] |
Xi YH, Peng H, Qin YM, et al. Bayesian analysis of heavy-tailed market microstructure model and its application in stock markets. Mathematics and Computers in Simulation, 2015, 117: 141-153. DOI:10.1016/j.matcom.2015.06.006 |
| [5] |
Horváth R, Šopov B. GARCH models, tail indexes and error distributions: An empirical investigation. The North American Journal of Economics and Finance, 2015, 37: 1-15. |
| [6] |
陶亚民, 蔡明超, 杨朝军. 上海股票市场收益率分布特征的研究. 预测, 1999(2): 57-58, 78. |
| [7] |
王志诚, 邓召明. 中国A股股票收益率的统计特征. 经济问题, 2001(12): 46-47, 53. DOI:10.3969/j.issn.1004-972X.2001.12.020 |
| [8] |
刘玄, 冯彩. 中国股市波动特征及非对称效应研究——以股改以来上证综指为例. 财会通讯, 2010(1): 76-78. |
| [9] |
吴鑫育, 马超群, 汪寿阳. 随机波动率模型的参数估计及对中国股市的实证. 系统工程理论与实践, 2014, 34(1): 35-44. DOI:10.12011/1000-6788(2014)1-35 |
 2018, Vol. 27
2018, Vol. 27


