近年来, 新兴体域网技术(Body Sensor Networks, BSN)[1,2]在人体健康监测、老年人预防跌倒、人体步态康复评价等领域得到广泛关注和应用. 其技术实现思路在于将多个采集传感节点(内嵌加速度计或陀螺仪传感器)佩戴于人体肩、手腕、肘、髋、膝、踝等关节处, 构建体域网运动模式获取人体运动数据信息, 为判别人体运动功能变化提供可靠数据. 基于体域网运动数据构建泛化性能优越的动作分类模型是近年来评价人体运动变化研究中的焦点问题, 也是国内外众多学者深入探讨的热点问题. 早期, 相关研究较多关注采用传统机器学习分类算法(诸如人工神经网络技术[3]、支持向量机[4–6]、决策树[7–9]、马尔科夫模型[10,11]等)构建体域网动作模式分类模型. 文献[3]提出一种基于二维加速度数据的三层神经网络动作模式分类模型, 所构建分类模型虽简单, 但识别率仅为85%; 文献[4]提出了一种基于无权重特征值的支持向量机体域网动作模式分类模型, 虽然识别率可高达97.21%, 但所设计分类算法复杂度高、耗时, 难以推广实际应用. 文献[11]提出一种基于半马尔科夫模型(Semi-Markov Conditional Random Fields)的体域网动作模式分类算法, 适用范围虽广, 但该算法需大量训练样本数据准确获得模型参数, 且最高识别率仅为88.47%. 此外, 早期相关研究较多基于四种动作模式探讨相关动作模式分类模型性能, 局限性较强, 难以准确判别体域网动作模式连续变化状况. 近年, 一种新兴稀疏表示分类(Sparse Representation Classification, SRC)算法在体域网动作模式识别研究中受到广泛关注[12,13]. 其基本思路: 将所有训练样本构建一个过完备字典, 准确稀疏表示测试样本(即, 与测试样本同类为非零系数, 非同类为零系数), 将体域网动作模式分类问题转化为测试样本稀疏表示系数求解问题, 然后基于所求解的稀疏表示系数定义残差确定测试样本类别. 文献[14]基于多传感节点加速度数据, 提出一种基于稀疏表示分类算法的的分布式体域网动作模式识别模型, 对13种不同动作模式分类, 平均识别率可达93.5%. 文献[13]提出一种基于单个传感节点加速度数据的人体动作模式稀疏表示分类算法, 对9种不同动作模式分类, 平均识别率可达95.3%. 虽然近年相关研究基于稀疏表示分类算法探讨人体动作模式连续变化状况取得较大进展, 但仍忽视由大量高维训练样本数据所构建的较大过完备字典对体域网动作模式分类算法性能的影响. 更重要的是, 近年相关研究大多采用简单平均叠加方法计算测试样本稀疏表示余差, 难以准确逼近不同动作模式在空间的分布状况, 也可能影响其分类性能. 如何在基于大量训练样本数据优化设计规模较小过完备字典的基础上, 准确估计逼近测试样本残差分布, 对于减少分类计算复杂度和时间、提高体域网动作模式分类性能至关重要, 也是近年相关研究探讨的热点问题.
近年来, 一种基于K-SVD学习算法[15]优化设计过完备字典在人脸稀疏表示识别、动态手势稀疏表示识别研究中得到广泛应用, 其基本思路就是基于优化学习算法, 从大量训练样本数据中获得优化过完备字典, 即可有效减少样本数据量, 又可准确稀疏表示测试样本, 确保判别信息不丢失. 上述研究成果为我们优化设计过完备字典提供了可借鉴思路. 此外, 近年一些相关研究提出了基于最大似然估计(Maximum Likelihood Estimation, MLE)模型[16,17]准确逼近稀疏表示残差, 其基本思想就是将余项的求解由l1或l2范式优化转化为一个似然估计算子, 利用最大似然函数, 更加准确估算稀疏表示残差值. 目前, 就相对于由l1或l2范式优化而言, 基于最大似然估计模型构建稀疏表示体域网动作模式分类算法, 使体域网动作模式训练样本所得最大似然估计函数更具有通用性, 能够获得更精确的测试样本表示残差, 有效提升体域网动作模式分类性能.
为此, 本文提出了一种基于K-SVD的最大似然稀疏表示体域网动作模式分类新算法, 其基本思想: 首先基于K-SVD优化学习算法, 将不同动作模式训练样本按其所属类别分组优化训练, 避免各类样本数据训练时相互干扰, 得到不同动作模式类别所属的子字典, 然后将子字典拼合构成一个完整字典, 准确稀疏表示测试样本, 最后基于最大似然稀疏模型准确估算稀疏表示系数残差, 有效提高动作模式分类性能. 本研究采用包含多传感数据的人体动作数据库WARD[14]验证本文所提算法有效性. 与传统稀疏表示分类算法相比较, 本文所提算法能够准确估计测试样本稀疏表示残差, 显著提高体域网动作模式识别率.
1 基于K-SVD的最大似然稀疏表示体域网动作分类算法本文所提算法旨在将K-SVD优化学习算法和最大似然估计相结合, 优化设计过完备字典, 基于较少训练样本数据准确稀疏表示测试动作样本, 然后构建测试样本稀疏表示残差最大似然估计模型, 判断其类别. 算法框架如图1所示, 由优化设计过完备字典的训练阶段和基于最大似然稀疏表示的动作识别阶段组成. 训练阶段主要是基于K-SVD分别每个动作类别优化学习获得子字典, 然后将所有优化子字典整合一个完整字典, 有效减少冗余样本数据, 准确稀疏表示测试样本. 识别阶段主要是采用最大似然估计模型估算稀疏表示余差分布密度函数, 然后基于余差分布密度函数求解测试样本稀疏表示残差, 判别测试样本所属类别.
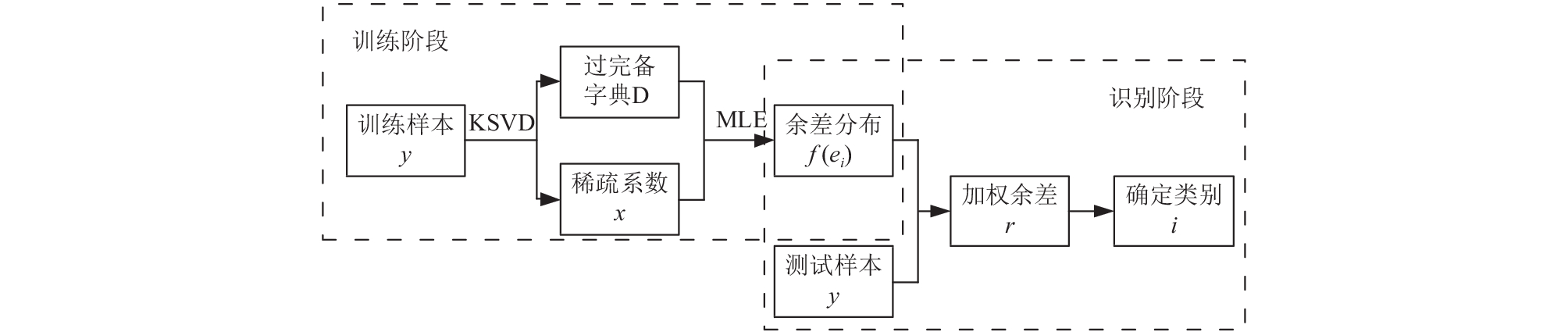
|
图 1 最大似然估计稀疏表示分类算法整体框图 |
1.1 基于K-SVD优化设计过完备字典
K-SVD是近年来提出的一种非常经典的字典训练算法, 其基本思想是依据误差最小原则, 对误差项进行SVD分解, 选择使误差最小的分解项作为更新的字典原子和对应的原子系数, 经过不断的迭代从而得到优化的解. 本研究为有效降低较大过完备字典对稀疏表示分类算法复杂度的影响, 以及避免不同动作类别的相互干扰, 提出基于动作类别的K-SVD优化设计过完备字典, 减少冗余动作样本信息. 假设包含所有动作类别的样本训练集表示为
| $\begin{array}{l}\left\langle {{D_i},{X_i}} \right\rangle = \arg \min \left\{ {\left\| {{Y_i} - {D_i}X} \right\|_2^2} \right\}\\\qquad s.t.\;\;\;\;\forall j,{\rm{ }}{\left\| {{x_j}} \right\|_0} \le {T_0}\end{array}$ | (1) |
式中,
基于上述步骤, 可得到由每一动作类别的子字典级联而成的一个完整优化过完备字典D, 既可减少字典规模, 又可有效确保动作样本中的判别信息不丢失.
1.2 最大似然稀疏表示动作分类模型基于所得优化过完备字典D, 可将测试样本y稀疏表示为:
| $y = Dx + \sigma $ | (2) |
式中, σ表示为误差容限, 尽可能确保稀疏表示系数
| $\widehat x = \arg \min {\left\| x \right\|_1}\;\;\;\;{\rm{s.t.}}\;\;\;\;\left\| {y - Dx} \right\|_2^2 \le \sigma $ | (3) |
式中, 约束条件要求余项
将字典D改写为
在稀疏表示模型中, 系数x具有稀疏性约束. 因此, 系数x的最大似然估计求解可以转化为式(4)所示的最小优化问题.
| $\widehat x = \arg \min \sum\nolimits_{i = 1}^n {{\rho _\theta }\left( {{y_i} - {d_i}x} \right)} \;\;\;\;{\rm{s.t.}}\;\;\;\;{\left\| x \right\|_1} \le \sigma $ | (4) |
一般来说, 余差e不符合高斯分布. 但是, 可以假设余差e的概率密度函数
设
| ${\widehat F_\theta }\left( e \right) = {F_\theta }\left( {{e_0}} \right) + {\left( {e - {e_0}} \right)^{\rm{T}}}F{'_\theta }\left( {{e_0}} \right) + {R_1}\left( e \right)$ | (5) |
式中,
| ${W_{i,i}} = \rho {'_\theta }\left( {{e_{0,i}}} \right)/{e_{0,i}}$ | (6) |
根据函数
| $\widehat x = \arg \min \left\| {{W^{1/2}}\left( {y - Dx} \right)} \right\|_2^2\;\;\;\;s.t.\;\;\;\;{\left\| x \right\|_1} \le \sigma $ | (7) |
比较式(7)和式(3)可以看出, 最大似然稀疏表示分类方法就是一个加权的稀疏表示模型. 由于权重矩阵W是一个对角矩阵,
本研究选用美国加州伯克利大学公开发布的包含多传感数据的人体动作模式数据库WARD. 该数据库采集20名受试者(13名男性, 7名女性, 年龄在19~70岁)13种不同动作模式: 站立、坐、躺、向前走、向左转、向右转、上楼、下楼、慢跑、跳、推轮椅、顺时针走、逆时针走. 每名受试者要求佩戴5个相同传感节点(内嵌一个三轴加速度计传感器和一个二轴陀螺仪), 分别置于左手腕、右手腕、左足踝、右足踝、腰部. 采用率设置为30 Hz. 本研究选用上述前11种动作模式数据验证本文所提算法有效性.
为确保所选动作模式数据信息完整性, 本文采用滑动窗口方法截取数据段, 窗口长度设置为200点. 选用三个方向的加速度数据和二个方向的陀螺仪数据定义采样数据向量维数为m=1000. 采用五阶平滑滤波对所选样本数据消噪.
为客观评价本文所提算法的分类性能, 我们采用留一交叉验证法, 即从所有20名受试者(每名受试者每种动作取5个样本)任意选取19名受试者数据作为训练样本集, 剩余1名受试者作为测试样本. 为确保动作样本训练、测试的可靠性, 上述交叉验证任意重复75次, 取最终平均结果作为分类器的识别率.
2.2 优化设计过完备字典由于样本数据维数为m=1000, 含一些冗余信息, 影响优化过完备字典的获取和分类器的最优性能. 在实验中, 我们采用随机投影方法压缩数据, 降低样本数据冗余信息. 压缩率(Compressive Proportion, cp)的定义如式(8).
| ${\rm{cp}} = m'/m$ | (8) |
式中,
| 表 1 本文算法基于不同压缩率的识别率和运行时间 |
从表1可以看到, 识别率和运行时间均随压缩率的增大而增大, 但压缩率为0.5时能够获得与压缩率为1时几乎相同的最大识别率, 运行时间却明显减少(约7.2秒). 这些结果表明, 最优压缩率为0.5. 因为当cp=0.5时, 压缩数据不仅可包含与原始数据几乎相同的动作模式差异信息, 同时可以有效降低本文所提算法复杂度, 提高动作分类性能.
在选取最优压缩率为0.5状况下, 我们进一步评估了基于本文所提算法选取优化过完备字典对动作分类性能的影响. 实验中, 每种动作训练样本数量选取为95. 图2给出了选取不同字典对动作分类性能的影响结果. 从图2可以看到, 本文所提算法随选取字典大小变化而变化. 当选取字典大小从10增加到40时, 动作识别率上升至最大(约95%); 其后, 识别率呈下降趋势. 这些结果表明, 字典规模过小, 难以包含动作模式完整差异信息; 字典规模过大, 所选样本数据必含过多冗余信息, 两者均影响动作分类性能. 但通过优化学习选取规模适当字典, 既可包含动作模式完整差异信息, 又可降低样本数据冗余信息, 有效提高动作模式分类性能.
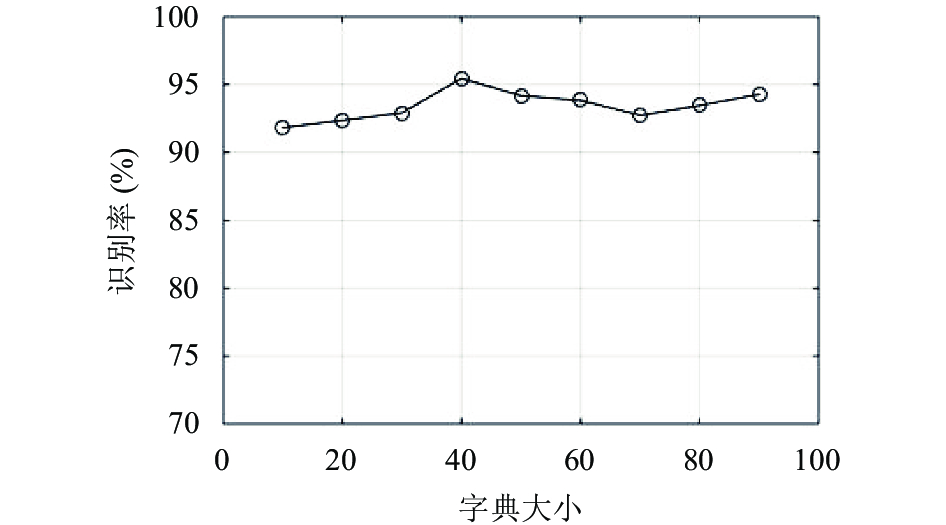
|
图 2 基于不同字典大小的识别率变化结果 |
2.3 最大似然稀疏表示动作分类性能
实验中, 我们选取传统的近紧邻算法(NN)、稀疏表示分类算法(SRC)、基于K-SVD的稀疏表示分类算法(KSVD+SRC), 作为比较, 进一步客观评价本文所提算法(KSVD+MLE)的有效性. 最优字典选取为40, 其比较结果如图3所示.
从图3可以看到, 四种动作分类算法动作识别率均随数据维度增长而增长, 比较而言, 本文所提算法(KSVD+ MLE)可获得最大识别率(96.36%), 分类性能明显优于其他所选三种分类算法性能, NN动作分类性能最差. 这些结果表明, 本文所提最大似然稀疏表示模型能够准确估计动作模式稀疏表示系数残差, 有效提高动作模式分类性能.

|
图 3 基于不同动作分类算法的比较结果 |
此外, 从图3中我们观察到, 基于SRC的动作分类性能(识别率为92.27%)明显优于基于KSVD+ SRC的动作分类性能(83.64%), 原因是K-SVD优化字典难以为SRC算法提供精确的稀疏表示系数残差, 影响其分类性能.
此外, 在实验中, 我们基于最优选取字典以及最优压缩率, 验证本文所提算法对所选11种动作模式分类性能, 进一步评估本文所提算法对连续动作模式分类有效性. 其分类混淆矩阵如表2所示. 从表2可以看到, 本文所提算法对11种不同动作模式识别率均达到94%以上, 平均识别率高达96%以上. 特别是, 站立、躺、左转、右转等动作识别率均可高达98%以上. 作为对比, SRC算法对所选11种动作模式的分类混淆矩阵如表3显示. 可以看出, SRC算法对坐、上楼、下楼、推轮椅四种动作模式识别率均在90%以下, 平均识别率仅为92%, 比之本文所提算法平均识别率低4%. 综上, 本文所提算法能够准确估计动作模式稀疏表示系数残差分布, 可有效识别动作模式连续变化.
3 结论与展望本文提出了一种基于K-SVD的最大似然稀疏表示动作分类算法. 该算法可有效利用K-SVD优化学习算法, 将不同动作模式训练样本按其所属类别分组优化训练, 避免各类样本数据训练时相互干扰, 将不同动作模式类别所属的子字典拼合一个完整字典, 准确稀疏表示测试样本, 使最大似然稀疏模型准确估计稀疏表示系数残差, 有效提高动作模式分类性能, 有助于判别动作模式连续变化.
| 表 2 本文所提算法基于11种动作信号的分类混淆矩阵 |
| 表 3 SRC算法基于11种动作信号分类混淆矩阵 |
| [1] |
Movassaghi S, Abolhasan M, Lipman J, et al. Wireless body area networks: A survey. IEEE Communications Surveys & Tutorials, 2014, 16(3): 1658-1686. |
| [2] |
Rawat P, Singh KD, Chaouchi H, et al. Wireless sensor networks: A survey on recent developments and potential synergies. The Journal of Supercomputing, 2014, 68(1): 1-48. DOI:10.1007/s11227-013-1021-9 |
| [3] |
Randell C, Muller H. Context awareness by analysing accelerometer data. The Fourth International Symposium on Wearable Computers. Atlanta, GA, USA. 2000. 175–176.
|
| [4] |
He ZY, Liu ZB, Jin LW, et al. Weightlessness feature-A novel feature for single tri-axial accelerometer based activity recognition. 19th International Conference on Pattern Recognition. Tampa, FL, USA. 2008. 1–4.
|
| [5] |
He ZY, Jin LW. Activity recognition from acceleration data based on discrete consine transform and SVM. Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics. San Antonio, TX, USA. 2009. 5041–5044.
|
| [6] |
He ZY, Jin LW. Activity recognition from acceleration data using AR model representation and SVM. Proceedings of the Seventh International Conference on Machine Learning and Cybernetics. Kunming, China. 2008. 2245–2250.
|
| [7] |
Jatoba LC, Grossmann U, Kunze C, et al. Context-Aware mobile health monitoring: Evaluation of different pattern recognition methods for classification of physical activity. 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Vancouver, BC, Canada. 2008. 5250–5253.
|
| [8] |
Bao L, Intille SS. Activity recognition from user-annotated acceleration data. International Conference on Pervasive Computing. Linz and Vienna, Austria. 2004. 1–17.
|
| [9] |
Ermes M, Parkka J, Cluitmans L. Advancing from offline to online activity recognition with wearable sensors. 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Vancouver, BC, Canada. 2008. 4451–4454.
|
| [10] |
Zhu C, Sheng WH. Human daily activity recognition in robot-assisted living using multi-sensor fusion. 2009 IEEE International Conference on Robotics and Automation. Kobe, Japan. 2009. 2154–2159.
|
| [11] |
Vinh LT, Lee S, Le HX, et al. Semi-Markov conditional random fields for accelerometer-based activity recognition. Applied Intelligence, 2011, 35(2): 226-241. DOI:10.1007/s10489-010-0216-5 |
| [12] |
Wright J, Yang AY, Ganesh A, et al. Robust face recognition via sparse representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. DOI:10.1109/TPAMI.2008.79 |
| [13] |
Zhang M, Sawchuk AA. Human daily activity recognition with sparse representation using wearable sensors. IEEE Journal of Biomedical and Health Informatics, 2013, 17(3): 553-560. DOI:10.1109/JBHI.2013.2253613 |
| [14] |
Yang AY, Jafari R, Sastry SS, et al. Distributed recognition of human actions using wearable motion sensor networks. Journal of Ambient Intelligence and Smart Environments, 2009, 1(2): 103-115. |
| [15] |
Aharon M, Elad M, Bruckstein A. rmK-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
| [16] |
Yang M, Zhang L, Yang J, et al. Robust sparse coding for face recognition. 2011 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI, USA. 2011. 625–632.
|
| [17] |
胡正平, 宋淑芬. 基于类别相关近邻子空间的最大似然稀疏表示鲁棒图像识别算法. 自动化学报, 2012, 38(9): 1420-1427. |
| [18] |
Zhang J, Jin R, Yang YM, et al. Modified logistic regression: An approximation to SVM and its applications in large-scale text categorization. Proceedings of the Twentieth International Conference on Machine Learning. Washington DC, USA. 2003. 888–895.
|
 2018, Vol. 27
2018, Vol. 27



