2. 遵义医学院附属医院 信息科, 遵义 563003;
3. 遵义医学院 医学信息工程学院, 遵义 563003;
4. 沙子坡中学 教务处, 铜仁 555202
2. Information Section, Affiliated Hospital of Zunyi Medical College, Zunyi 563003, China;
3. School of Medical Information Engineering, Zunyi Medical College, Zunyi 563003, China;
4. Academic Affairs Office, Shazipo Middle School, Tongren 555202,China
工作流建模一直是工作流研究领域热点方向之一. 对工作流的研究, 有以活动为中心研究工作流的资源管理与配置、动态变更与实例迁移以及工作流的路径求取算法等; 也有因为以活动为中心缺乏组织人员和角色的重视而提出以角色为中心基于其它建模工具对工作流进行建模. 迄今为止, 基于Petri Nets、Agent、UML等建模工具产生了许多工作流模型. 其中, 西安交通大学的李宗斌、高新勤等人在文献[1,2]提出了工作流的的动态变更和实例迁移模型以及工作流区域识别算法与排序规则, 并指出动态变更主要是对工作流模型结构的添加/删除、结构转换和结构的组合, 他们在文献[3]中通过多色集合理论建立相关的围道矩阵对工作流建模并给出了工作流路径求取算法, 并在文献[4,5]中运用提出的离析运算为工作流过程推理和配置资源, 实现工作流过程与工作流资源的集成, 其中还对多色图的边进行了扩展, 将边分为连接、与分、或分、与合、或合. 北京航空航天大学软件工程研究院的徐亮、张莉等人在文献[6]通过扩展UML针对实时系统建立了实时工作流元模型, 主要考虑了工作流中的时间约束和异常处理, 对活动属性扩展了启动、执行时间与并发时间约束, 最后还定义了实时工作流描述语言. 同济大学的杨书新等人在文献[7]中提出了业务流程动态变更模型与业务过程实例动态迁移算法, 其目的是解决工作流管理系统中流程柔性演进变化问题. 南京大学的葛季栋等在文献[8]中用Petri Nets对工作流进行了分解并提出了面向交互的Petri Nets模型来对跨组织的工作流协同进行描述. 复旦大学的赵静、赵卫东等人在文献[9,10]中基于角色的视角对工作流进行了研究, 它们将提出了工作流日志挖掘与流程分解结合的角色识别算法, 最终生成与业务流程相关的角色树, 他们在文献[11]中还利用agent技术基于角色对工作流进行建模形成了一种面向角色的工作流多agent管理系统模型与原型. 以上这些研究构建的工作流模型体现出了活动间的逻辑关系, 缺乏活动间交互时涉及的资源等性质.
以活动为中心对工作流交互过程进行建模, 不仅需要考虑活动及其逻辑关系, 还需要考虑活动交互间消息的发送与接收以及相关资源的交互. 多色集合理论是在传统集合的基础上与模糊数学、数理逻辑等知识相结合形成的. 由于多色集合理论中对象的集合与元素都能被涂上不同的颜色来表示对象的性质, 用该理论研究工作流的交互过程较易描述工作流中活动的静态属性与动态行为, 并且通过本文提出的连接运算能够描述活动间交互涉及的消息与资源, 由矩阵与相关的规则构成工作流过程交互多色图模型, 使活动与交互的消息和资源进行良好的整合.
课题组前期在研究系统交互的过程中对多色集合理论进行了扩展, 为便于描述系统的动态行为, 因此提出了围道分割的思想, 将对象的整体性质F(A)分割成静态属性FS(A)与动态行为FD(A), F(A)=FS(A)∪FD(A). 并提出了单元素多色集合, 其中的对象集合A仅包含了一个元素, 那么对象的个人颜色就与对象的整体着色相同, 并在此基础上提出了实体聚合运算与功能聚合运算. 为了用围道矩阵描述活动的交互关系, 在矩阵中使用0、1、–1、2、–2分别表示活动间的顺序、并分、或分、并合、或合关系.
本文基于多色集合理论对工作流过程中活动的交互进行研究, 有助于工作流整体建模. 首先提出单元素二元组多色集合与多元素二元组多色集合; 其次为了能够完整地描述一个对象的静态性质与动态行为, 对普通的围道布尔矩阵进行了扩展, 使围道的边不再局限于单个的元素而是由多元组构成, 并对多色图中的节点进行了区域的划分; 最后, 对工作流交互过程的步骤进行分析, 用HIS与RIS间的交互为例验证.
1 基本理论 1.1 多色集合理论多色集合理论是在传统集合的基础上与模糊数学、数理逻辑以及矩阵相关知识结合而成的, 它的特点是使用相同的数学模型来仿真不同的对象[12], 由多色集合与多色图两部分构成.
1.1.1 多色集合[13]多色集合是在传统集合基础上对集合的整体及其元素进行着色, 用以表示对象的性质、属性、参数等特性以及对象与元素、元素与元素之间的关系. 如果集合中存在着多个元素, f(ai)表示元素ai∈A的个人颜色, F(A)表示对象A的整体着色, F(A)={F1(A), F2(A),…, Fj(A),…, Fp(A)}, 统一的颜色布尔矢量空间F包含了集合的整体着色F(A)和元素ai的个人着色f(ai), 即
| $\begin{aligned}{\left\| {c_{i(j)}} \right\|_{A,F(A)}} & =[A \times F(A)]\\& =\mathop {\left[ {\begin{array}{*{20}{c}}{{F_1}}& \cdots &{{F_j}}& \cdots &{{F_m}}\\{{c_{1(1)}}}& \cdots &{{c_{1(j)}}}& \cdots &{{c_{1(m)}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\{{c_{i(1)}}}& \cdots &{{c_{i(j)}}}& \cdots &{{c_{i(m)}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\{{c_{n(1)}}}& \cdots &{{c_{n(j)}}}& \cdots &{{c_{n(m)}}}\end{array}} \right]}\limits^{\begin{array}{*{20}{c}}\end{array}} \begin{array}{*{20}{c}}{{a_1}}\\ \vdots \\{{a_i}}\\ \vdots \\{{a_n}}\end{array}\end{aligned}$ | (1) |
多色集合的表达式为公式(2)[15].
| ${\rm{PS}} \! = \! (A,F(a),F(A),[A \! \times \! F(a)],[A \! \times \! F(A)],[A \! \times \! A(F)])$ | (2) |
若集合中只有一个元素, 那么f(a)=F(A), 其多色集合的表达式为公式(3).
| ${\rm{SPS}} = (A,F(a))$ | (3) |
被称为单元素多色集合. 并且还提出了单元素多色集合的析取与合取运算. 使得在描述单个元素时模型更加的简化[16].
1.1.2 多色图[17]多色图是在普通图G=(V, E)上对其边与节点进行着色, 并且多色图的边与节点都是由多色集合构成, 丰富了多色图的表达能力. PG=(F(G), PSA, PSC), 其中F(G)是图的整体着色, PSA是节点的多色集合, PSC是边的多色集合. 如果节点和边均有颜色, 那么F(G)=F(A)∪F(C); 如果节点无颜色, 那么F(G)=F(C); 反之F(G)=F(A). 在某些特殊情况下, 节点与边均无颜色, 那么多色图就退变为普通图, 因此, 普通图也是特殊的多色图.
1.1.3 二元组多色集合为更好地描述交互对象, 提出二元组多色集合, 对象间只要存在着交互行为, 必有一方是调用方, 一方是响应方. 将对象、个人颜色、整体着色都分割成二元组的形式, A=<AI, AP>,F(A)=<FI(A), FP(A)>, 其中,AI表示对象的调用方, AP表示对象的响应方, FI(A)表示对象调用方的整体性质, FP(A)表示响应方的特性. 多色集合中分割后的元素之间可能存在着某些联系, 例如, 对象aI可能会调用对象bp, 形成调用-响应布尔矩阵[AI×AP]等.
当集合A中包含多个元素时, 此时元素的整体着色就会与个人着色有区别, 会产生冗余的性质, 因此可以将典型的多色集合分割, 形成多元素二元组多色集合(Mult-elements Binary Polychromatic Sets, MBPS), 见公式(4).
| $\begin{align}{\rm{MBPS}} & = \bigg( < \! {{A}_{I}},{{A}_{P}}\! >,<\! {{F}_{I}}\left( a \right),{{F}_{P}}\left( a \right)\! >,<\! {{F}_{I}}\left( A \right),{{F}_{P}}\left( A \right) \! >, \\ & \quad \left[ {{A}_{I}}\times {{A}_{P}} \right],<\left[ {{A}_{I}}\times {{F}_{I}}\left( A \right) \right],\left[ {{A}_{P}}\times {{F}_{P}}\left( A \right) \right]>, \\ & \quad < \! \left[ {{A}_{I}}\times {{F}_{I}}\left( a \right) \right],\left[ {{A}_{P}}\times {{F}_{P}}\left( a \right) \right] \! >,\left[ {{F}_{I}}\left( A \right) \! \times \! {{F}_{p}}\left( A \right) \right] \! \bigg) \\ \end{align}$ | (4) |
如果A中只有一个元素, 那么F(A)=F(a), 多元素二元组多色集合可以简缩, 称其为单元素二元组多色集合(Single Binary Polychromatic Sets, SBPS), 其表达式为公式(5).
| $\begin{aligned}{\rm{SBPS}} & \! = \! (< \! {{A}_{I}},{{A}_{P}} \! > ,< \! {{F}_{I}}\left( A \right),{{F}_{P}}\left( A \right) \! > ,< \! \left[ {{A}_{I}}\times {{F}_{I}}\left( A \right) \right], \\ & \left[ {{A}_{P}}\times {{F}_{P}}\left( A \right) \right] \! > < \! \left[ {{A}_{I}} \! \times \! {{F}_{P}}\left( A \right) \right],\left[ {{A}_{P}} \! \times \! {{F}_{I}}\left( A \right) \right] \! > ) \\ \end{aligned}$ | (5) |
可以根据实际情况对成分进行增加或删除.
1.1.4 K元组围道矩阵用典型的围道矩阵描述对象的性质时, 围道的边都是对象的单个特征, 当一个对象存在着多个静态属性与动态行为时, 就会加大矩阵规模. 因此在围道矩阵中引入元组, 用元组将对象的静态属性与动态行为进行组合, 一方面可以减小矩阵的规模, 另外通过扩展的矩阵能够清楚地了解到对象的整体性质.
在K元组围道矩阵中, 矩阵的边是单个元素或多元组与多元组构成, 矩阵的值也不再是单个的布尔值, 也是由K元组组成, 并且K元组中的值是由0, 1组成, 便于矩阵之间进行运算. 其形式为公式(6).

|
(6) |
其中,cij是K元组,
(1) 析取计算
K元组矩阵的析取运算由原来布尔围道矩阵中单个元素的析取转换为元组与元组之间的析取运算. 如果围道表示功能元组, 那么元素的析取就能表示总体功能, 具体运算如公式(7) .
| $\begin{array}{*{20}{c}}{}&{ < F_1^1,F_1^2,F_1^3,F_1^4 > }&{ < F_2^1,F_2^2,F_2^3,F_2^4 > }&{ < F_3^1,F_3^2,F_3^3,F_3^4 > }&{ < F_4^1,F_4^1,F_4^3,F_4^4 > }\\\hline{{a_1}}&{ < 1,0,0,1 > }&{ < 0,1,1,1 > }&{ < 0,0,1,1 > }&{ < 0,1,0,1 > }\\ \vee &{}&{}&{}&{}\\{{a_2}}&{ < 1,0,0,0 > }&{ < 0,0,0,1 > }&{ < 1,1,1,1 > }&{ < 1,1,0,0 > }\\\hline{{a_1} \vee {a_2}}&{ < 1,0,0,1 > }&{ < 0,1,1,1 > }&{ < 1,1,1,1 > }&{ < 1,1,0,1 > }\end{array}$ | (7) |
元素a1与a2具有<F11, F14>, <F22, F23, F24>, <F31, F32, F33, F34>, <F41, F42, F44>的性质.
(2) 合取运算
ai∧aj表示ai, aj具有的共同性质, 当元组中两个值同为1时, 结果才为1, 否则为0. 在工作流活动的交互过程中, 将每个活动拥有资源、方法用围道布尔矩阵表示后, 对它们进行合取运算, 可得出两个或多个活动间拥有的相同资源、方法等. 在信息安全方面, 通过该运算可表示两个角色拥有的共同权限, 数据等.
(3) 顺序连接运算
如果两个围道布尔矩阵, [A×F(A)]是i×j的单元素或多元组矩阵, [A×F(B)]也是i×j的单元素或多元组矩阵, F(A), F(B)是单元素或K元组, 将F(B的围道和值分别与[A×F(A)]中的围道与值连接后构成二元组或2K元组, 如公式(8)所示. 具体矩阵运算如公式(9)所示.
| $\left[ {A \times F\left( A \right)} \right] \oplus \left[ {A \times F\left( B \right)} \right] = \left[ {A \times {\rm{ }} < F\left( A \right),F\left( B \right) > } \right]$ | (8) |
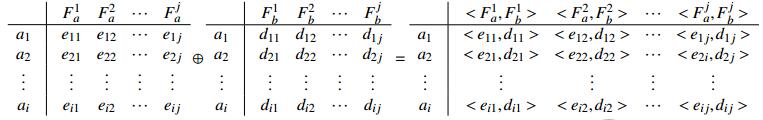
|
(9) |
(4) 自由连接运算
在实际运算的过程中, 存在着两个矩阵的行数与列数不相等, 此时, 顺序连接运算不适用于该种情况.
两个矩阵[A×F(A)]与[B×F(B)]的行对应的运算对象不相同并且行数也不同时, 可以将其中一个矩阵的行对象移入另一个矩阵中, 并且列上标是两个矩阵的对应列组合而成, 其值也是两个矩阵中对应列的值组合而成.
对某个对象进行多色集合表达时, 首先对该对象与其相应的属性形成普通的围道布尔矩阵, 然后通过连接运算形成多元组围道布尔矩阵, 在最终结果的围道元组中, 能够清楚地知道对象完成某个功能需要哪些资源、数据、方法等.
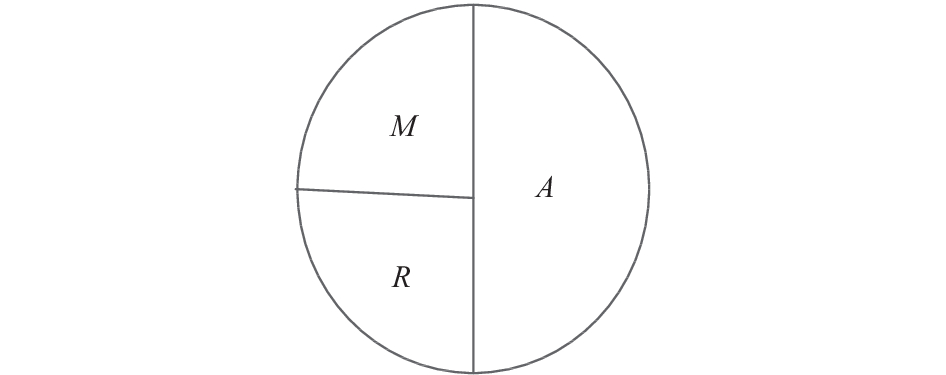
1.1.5 多色图节点的扩展在用多色图表示工作流中活动的交互时, 文献[17]提出对多色图的边进行分类, 以明确活动交互间的关系, 但是活动交互所需的数据、应用程序等资源、时间约束条件、消息等在图中不能够体现出来, 因此, 对多色图中的节点进行区域划分, 将节点分为三部分分别表示资源R、消息M、活动A, 如图1所示.
|
图 1 节点区域划分图 |
图1中, M是活动A的前驱活动向活动A发送的消息, 即活动A收到的消息为M, R是活动A向其后继活动传输的信息资源. 可以根据实际情况对多色图中的节点进行区域划分.
2 系统间交互分析在一个系统中包含许多的类, 类是现实世界中实体的形式化描述, 它将该实体的数据和函数封装在一起. 因此, 类可以表现为静态属性和动态行为, 其静态属性可以用一般的布尔矩阵“类—属性”围道矩阵描述, 其动态行为用以上提出的K元组围道矩阵对其进行描述. 类中的方法M (Method)包含参数P (Paramater), 局部变量LV (Local-Varation), 返回的结果R (Result).
系统间的交互实际就是类实例化后产生的对象间方法的调用与响应, 那么, 方法M就应该分割成<调用方, 响应方>, 即M=<MI, MP>, 调用方与响应方的个人性质F(m)=<FI(m), FP(m)>, 即FI(m)=(PI, LVI, RI), FP(m)= (PP, LVP, RP), 多个方法组合会产生一些新的功能F(M), 用多色集合描述系统间的交互过程步骤如下.
(1) 分析系统的某一模块中包含的类Class, 形成一个类集C;
(2) 将类中的静态属性抽象成FS(C), 动态性质抽象成为FD(C), 那么, FD(C)=(<MI, MP>, <FI(m),FI(m)>, <FI(M), FI(M)>);
(3) 对步骤(2)中的调用方和响应方的方法M分别进行描述, 形成“方法—参数”、“方法—局部变量”、“方法—结果”的布尔矩阵, 即[M×P]、[M×LV]、[M×R];
(4) 方法之间的调用与响应形成方法交互布尔矩阵, 即[MI×MP];
(5) 利用本文提出的连接运算对步骤(3)与步骤(4)中的矩阵进行连接运算. 最终形成[MI×<MP, PP, LVP, RP>]的矩阵.
因此, 系统间交互多色集合SIBPS (System of Interaction between Polychromatic Sets)可以描述为公式(10).
| $\begin{split}S\! IBPS = (C,{F_S}\left( C \right), < \! {M_I},{M_P} \! > , < \! {F_I}\left( m \right),{F_P}\left( m \right) \! > , \!\!\! \\\quad < \! {F_I}\left( M \right),{F_P}\left( M \right) \! > ,\left[ {{M_I} \times < \! {M_P},{P_{P,}},L{V_P},{R_P} \! > } \right)\!\!\! \end{split}$ | (10) |
根据最后得出的4元组矩阵能明确地知道两个系统间交互涉及的方法以及调用方法后产生的结果.
3 作流过程活动交互以活动为研究对象, 工作流过程间的交互表现为活动之间消息的发送与接收以及相关资源的交互. 为了构建出工作流过程交互的多色图模型, 首先应该分析工作流中的活动、消息、资源, 然后形成相关的普通围道矩阵; 其次, 对这些矩阵进行连接运算得出对象的完整描述矩阵; 最后, 利用相关规则形成多色图模型. 工作流过程交互分析的流程图如图2所示.
3.1 规则(1) 在矩阵[A×A]中, 如果活动ai与活动aj之间对应的值不为空, 则ai是aj前驱活动, aj是ai后继活动.
(2) 如果矩阵中活动ai的列的值全为空, 则活动ai是起始活动; 如果活动aj的行的值全为空, 则aj是终止活动.

|
图 2 工作流交互分析流程图 |
3.2 工作流过程交互分析
工作流过程间的交互从整体上来说表现为角色之间的交互, 其可细化为活动之间的直接交互. 在工作流过程交互中, 以活动为研究对象, 用集合A表示, 活动间交互所需的数据、应用程序、约束条件等活动的性质用F(A)描述, 用O表示包含活动的对象角色, F(O)描述角色的性质, 其中, 角色之间是通过消息的传递进行交互的, 因此, 消息集M、部分活动集G是角色的性质. 角色与活动形成布尔矩阵[O×A], 角色与其对应的性质用[O×F(O)]描述, 工作流中活动间的交互表现为矩阵[A×A], 活动集A与活动性质形成矩阵[A×F(A)]. 因此, 工作流过程活动的交互用交互多色集合IPS (Interaction Polychromatic Sets)描述为公式(11).
| $\begin{split}IPS & = \left( {O,A,F\left( O \right),F\left( A \right),\left[ {O \times A} \right],\left[ {O \times F\left( O \right)} \right],} \right.\\& \quad \left.{ \left[ {A \times A} \right],{\rm{ }}\left[ {A \times F\left( A \right)} \right]} \right)\end{split}$ | (11) |
可将交互多色图划分为三部分, 如果存在着分支结构, 其中, 左分支中的活动构成活动集Gi, 右分支中的活动构成活动集Gk, 剩余除起始逻辑活动与结尾逻辑活动外的活动构成Gj.
3.2.1 工作流过程交互分析步骤对工作过程的交互建模不是一蹴而就的, 需要先分析交互中涉及的活动、消息、资源, 然后构成相关的矩阵.
工作流过程交互步骤:
(1) 识别此过程中涉及的对象角色集O、活动集A、消息集M并形成[O×F(O)];
(2) 形成活动交互矩阵[A×A]以及活动交互消息矩阵[A×A×M]、活动交互资源矩阵[A×A×R];
(3) 运用连接运算形成过程交互矩阵[A×A×F(A)], 最后可形成交互多色图, 并根据交互多色图形成部分活动集G以及活动集矩阵[G×G].
文献[5,17]中提出了对多色图的边进行分类, 活动间存在着五种关系: 顺序、并分、或分、并合、或合.
| 表 1 活动间关系标识 |
3.2.2 工作流过程交互多色图建模
建立多色图模型前, 需要完成3.2.1中工作流过程交互分析的前两步, 然后再对相应的矩阵进行操作.
交互多色图的构成步骤:
(1) 利用3.1中的规则找到起始活动ai;
(2) 在活动围道矩阵中找到起始活动ai的后继活动aj, 如果ai与对应aj的值为0, 则用顺序关系进行描述; 如果有多个后继活动并且对应的值为1, 则用并分关系进行描述; 如果有多个后继活动并且值为–1, 则用或分进行描述; 如果对应的值为2, 则用并合描述; 如果对应的值为–2, 则用或合描述;
(3) 根据矩阵[A×A×M]、[A×A×R]分别找到相应活动的接收的消息与活动发出的信息流;
(4) 如果用3.1中规则判断活动ak是否是终止活动, 若不是终止活动, 继续步骤(2)、(3); 反之, 结束.
4 实例医院HIS与RIS的门诊过程中, 病人首先到挂号处排队挂号, 然后到门诊分诊台分诊, 门诊医生利用门诊医生工作站根据需要开出放射检查医嘱, 收费处根据检查医嘱进行划价收费, 检查科医生根据检查申请信息进行检查预约安排, 最后病人根据时间安排到放射科做检查, 放射科医生根据放射科医生工作站对检查影像进行读片, 并书写检查诊断报告, 同时检查完后, 影像图片会自动上传至PACS, 门诊医生可以通过医生工作站查看病人影像检查报告并进一步作出治疗方案.
此过程中, 对象角色包含病人Patient, HIS, LIS, 即O=(Patient, HIS, LIS).
活动集A=(b1, a11, a12, a13, a14, a21, a22, a23, a24, b2), 其中, b1, b2是无意义的活动, 只是表示活动的开始与结束.
消息集M=(M1, M2, M3, M4, M5, M6, M7, M8).
资源集R=(R1, R2, R3, R4, R5, R6, R7, R8,R9,R10).
三个集合中元素含义见表2至表4. 用0、1、–1、2、–2分别标识活动间的顺序、并分、或分、并合、或合, 可以构建出活动关系矩阵[A×A], 见图3. 若活动ai与aj无任何关系, 则其对应的值为空; 若为0, 表示存在顺序关系; 若为1, 表示并分关系; 若为–1, 表示或分关系; 若为2, 表示并合关系; 若为–2, 表示或合关系.
| 表 2 活动集A各元素含义 |
| 表 3 消息集M各元素含义 |
| 表 4 资源集R各元素含义 |
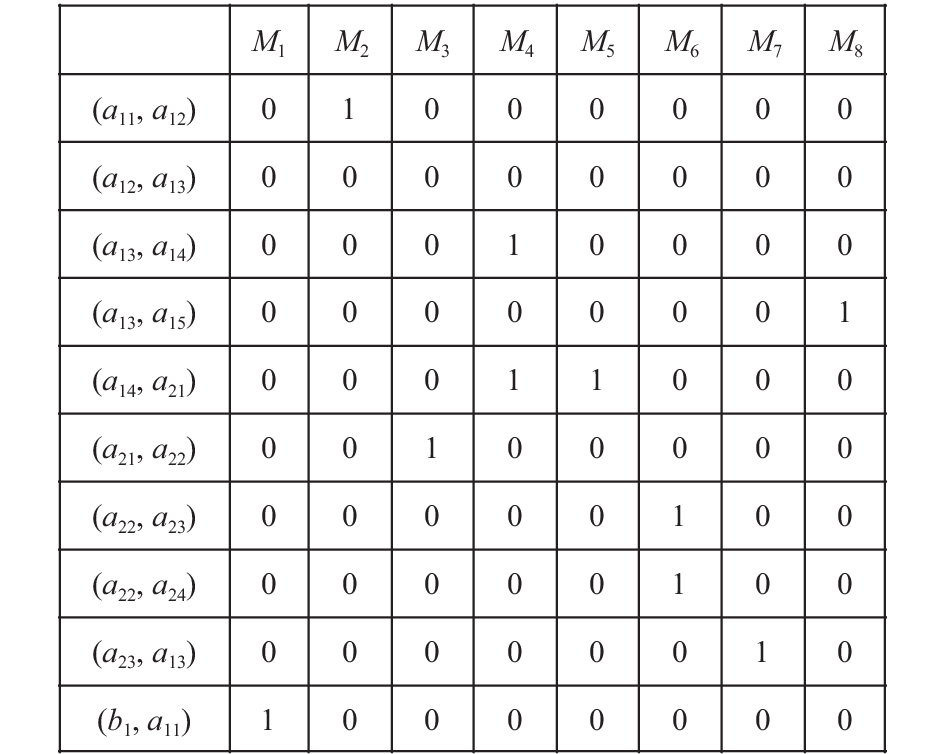
如果活动aj收到ai的消息Mk, 则矩阵中对应的值为1, 否则, 值为0, 见图4.
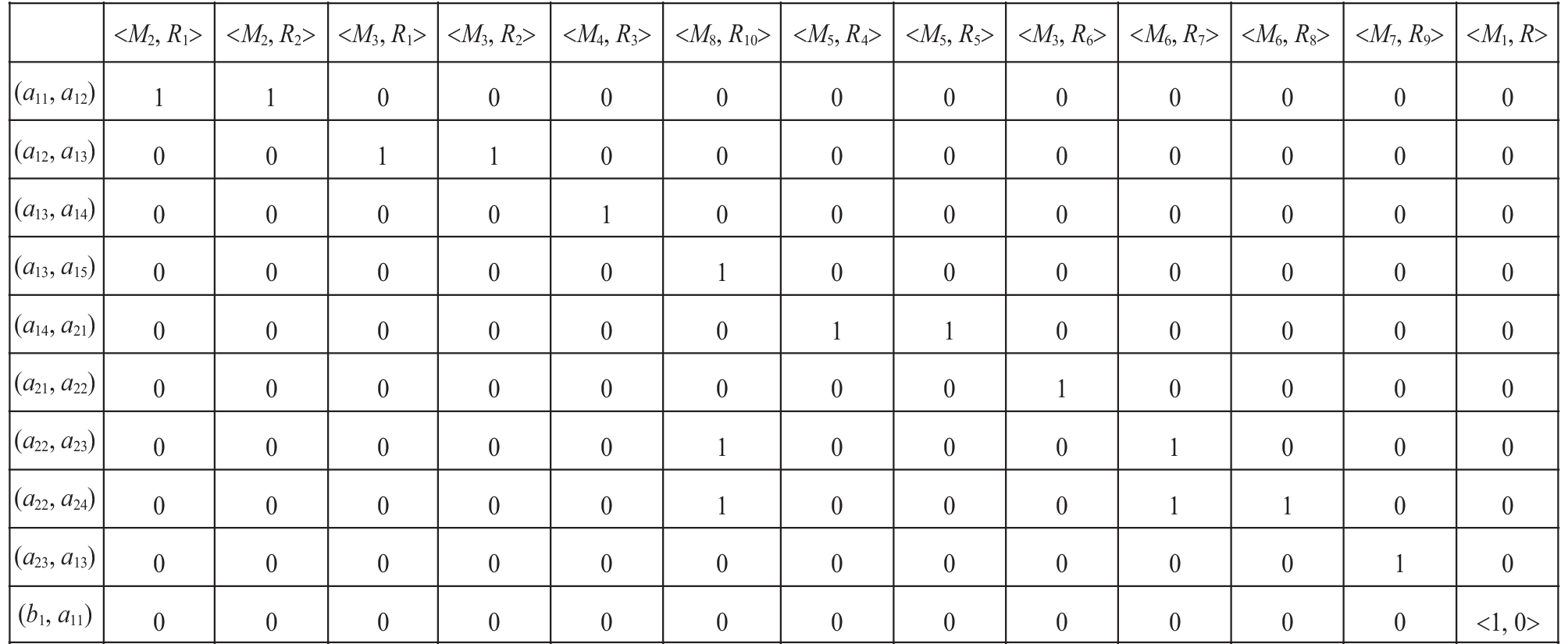
通过前面所提出的自由连接运算, 将活动间事件关系矩阵与活动间信息流关系矩阵整合成一个矩阵, 能够清楚地知道活动间交互的消息与所需要的信息资源, 如图5所示. 根据图5以及3.1中的规则和表1可以形成工作流过程交互多色图模型, 如图6所示.
由图7可知, G1与G2对应的值为1, G3与G1对应的值为1, HIS与RIS之间工作流交互. 图8矩阵中, 若活动ai与aj之间存在信息流, 则值为1, 反之, 为0.

|
图 3 活动交互矩阵[A×A] |
|
图 4 活动间消息关系矩阵[A×A×M] |
|
图 5 活动过程交互矩阵[A×A×F(A)] |

|
图 6 工作流过程交互多色图 |

|
图 7 矩阵[G×G] |

|
图 8 活动间信息流关系矩阵[A×A×R] |
5 总结
本文采用多色集合理论对不同系统间工作流过程的交互进行了研究, 将元组与多色集合相结合, 提出K元组围道矩阵以及它的析取、合取与连接运算, 有利于描述对象的整体性质, 通过扩展的K元组围道矩阵能够同时描述对象的静态属性与动态行为. 运用该运算对工作流交互中的消息以及资源进行整合, 建立了工作流交互多色图模型. 该模型中不仅体现了活动及其逻辑关系, 还描述了与活动相关的性质与行为. 但是, 有关工作流过程活动间交互产生的安全问题没有进行考虑, 下一步将对工作流交互中涉及的安全问题展开研究.
| [1] |
高新勤, 李宗斌, 杜轩. 工作流管理系统动态变更模型与实例迁移方法研究. 计算机集成制造系统, 2008, 14(8): 1521-1528. |
| [2] |
Gao XQ, Wang XP, Li Y, et al. Workflow dynamic change and instance migration approach based on polychromatic sets theory. International Journal of Computer Integrated Manufacturing, 2016, 29(4): 386-405. DOI:10.1080/0951192X.2015.1034181 |
| [3] |
朱景, 李宗斌, 高新勤. 基于多色集合的工作流建模及路径求取算法. 西安交通大学学报, 2006, 40(3): 348-352. |
| [4] |
高新勤, 李言, 杨明顺, 等. 基于多色集合离析运算的工作流资源管理与配置方法. 计算机集成制造系统, 2011, 17(9): 1905-1912. |
| [5] |
Gao XQ, Xu LD, Wang XP, et al. Workflow process modelling and resource allocation based on polychromatic sets theory. Enterprise Information Systems, 2013, 7(2): 198-226. DOI:10.1080/17517575.2012.745617 |
| [6] |
徐亮, 张莉, 樊志强. 一种基于UML的实时工作流建模方法研究. 计算机研究与发展, 2010, 47(7): 1184-1191. |
| [7] |
杨书新, 王坚, 马福民. 工作流管理系统的流程柔性动态变更研究. 计算机应用, 2006, 26(11): 2736-2738. |
| [8] |
葛季栋, 胡海洋, 周宇, 等. 一种基于不变量的工作流协同模型分解方法. 计算机学报, 2012, 35(10): 2169-2181. |
| [9] |
赵静, 赵卫东. 基于工作流日志挖掘的流程角色识别. 计算机集成制造系统, 2006, 12(11): 1916-1920. DOI:10.3969/j.issn.1006-5911.2006.11.032 |
| [10] |
赵卫东, 戴伟辉. 基于角色的跨组织工作流研究. 系统工程与电子技术, 2003, 25(8): 954-958. |
| [11] |
赵卫东, 黄丽华. 面向角色的多agent工作流模型研究. 管理科学学报, 2004, 7(2): 55-62. |
| [12] |
高新勤, 李宗斌, 赵姗姗. 基于多色集合理论的概念设计建模和推理技术研究. 中国机械工程, 2006, 17(3): 255-259. |
| [13] |
Li ZB, Xu LD, Zhao SS. Polychromatic sets theory and its application in enterprise information systems. In: Tjoa AM, Xu L, Chaudhry SS, eds. Research and Practical Issues of Enterprise Information Systems. IFIP International Federation for Information Processing. Boston, MA: Springer, 2006. 721–728.
|
| [14] |
多色集合在加工系统建模与分析时的应用. 西安交通大学学报, 2001, 35(9): 926-929, 986. |
| [15] |
李丹. 基于多色集合的冷链物流仓储流程优化研究[硕士学位论文]. 西安: 陕西科技大学, 2014.
|
| [16] |
杨敏, 王晓华, 冉梅梅. 基于多色集合理论的两系统间互操作方法. 计算机系统应用, 2017, 26(9): 128-134. DOI:10.15888/j.cnki.csa.005930 |
| [17] |
李春玲. 基于多色图理论的离散制造企业生产物流系统建模与优化[硕士学位论文]. 沈阳: 沈阳大学, 2014.
|
| [18] |
王颂, 李云龙, 陈富民. 基于多色集合的飞机连接装配工艺规划与资源配置. 计算机集成制造系统, 2013, 19(2): 411-420. |
 2018, Vol. 27
2018, Vol. 27