2. 西安电子科技大学 计算机学院, 西安 710071
2. School of Computer Science and Technology, Xidian University, Xi’an 710071, China
NAND闪存是非易失性存储器(Non-Volatile), 由于其高容量、低成本、读写速度快等优点被广泛的应用于消费电子产品中, 如手机、笔记本电脑等[1,2]. 多级单元(Multi-Level Cell, MLC)技术成为提高NAND型闪存数据容量和降低成本的有效手段. 然而, 目前NAND闪存芯片封装尺寸减少, MLC闪存浮栅中可存储的电子变少、相邻电位窗口间隔变窄、相邻MLC单元之间的寄生耦合电容效应变大, 单元间干扰(Cell-to-Cell Inference, CCI)成为影响闪存阈值电压失真的主要原因. 因此, NAND闪存的可靠性急剧下降[3].
随着NAND闪存封装尺寸减小和MLC技术的应用, 传统的纠错码已不能满足MLC型NAND闪存的可靠性要求[4,5]. LDPC码是具有低译码复杂度和逼近香农限的良好性能成为提高MLC型NAND闪存可靠性的研究方向之一[3–6]. Wang和Courtade研究利用闪存信道的统计信息获得更好的LDPC码软判决译码性能[7]. 对于MLC闪存软信息的准确度会影响到LDPC码译码器的纠错性能. 基于均匀感知策略的MLC电压感知方法需要提高感知精度才能获取高精度的对数似然比(Log-Likelihood Ratio, LLR)值. 但是, 高感知精度会消耗更长的感知时间, 影响闪存的读取速度. 本文提出了一种基于非均匀感知策略的MLC闪存最小和译码方法, 该方法是对MLC相邻阈值电压分布重叠区间进行均匀划分, 而不采用均匀感知策略中将每个MLC状态的阈值电压区间的均匀划分方法. 在相同的感知精度下, 相比于均匀感知策略, 非均匀感知策略能够提高LLR的准确度, 进而能够在LDPC码最小和译码过程中传递更多的有效信息, 提高译码器的译码性能.
1 MLC型NAND闪存NAND闪存的最小存储单元是带浮栅(Floating Gate)的MOS晶体管. 其中浮栅被氧化绝缘层隔离, 电荷注入其中可以长期稳定保存(如图1所示). 浮栅中电荷数量决定闪存单元的阈值电压, 不同的阈值电压可以映射为不同的状态, 从而表示不同的数据.

|
图 1 闪存单元基本结构 |
MLC型NAND闪存通过一个浮栅单元存储4个不同电位表示2比特数据, 提高NAND闪存的数据存储密度. MLC型NAND闪存使用标准的格雷码来映射闪存单元中的四个状态
MLC闪存芯片在擦除操作(将浮栅中的电子移除)之后闪存单元的阈值电压可近似地使用一个高斯分布来表示. 因此使用公式(1)来表示MLC闪存单元擦除状态的阈值电压分布[8]:
| ${p_e}\left( x \right) = {p_{{s_0}}}\left( x \right) = \frac{1}{{{\sigma _e}\sqrt {2\pi}}}{\rm{exp}}\left\{-\frac{\left({x-{\mu _e}}\right)^2}{2\sigma_e^2}\right\}$ | (1) |
其中,
随着闪存封装尺寸的减小(65 nm及以下), 编程操作(向浮栅充电至不同的电位)使MLC闪存单元阈值电压增加, 其数学模型
| ${p_p}\left( x \right) = {p_{{s_1}|{s_2}|{s_3}}}\left( x \right) = \frac{1}{{{\sigma _p}\sqrt {2\pi } }}{\rm{exp}}\left\{-\frac{\left({x-{\mu _p}}\right)^2}{2\sigma_p^2}\right\}$ | (2) |
其中,
MLC阈值电压模型参数设置为: 擦除状态阈值电压分布概率密度函数

|
图 2 理想情况下的MLC阈值电压统计直方图 |
1.2 单元间干扰噪声模型的建立
MLC闪存由于单元间存在寄生耦合电容效应, 所以当MLC单元经过编程操作增加阈值电压之后, 这种电压的增量会对其邻近MLC单元的阈值电压产生影响, 这种影响称之为单元间干扰[9](如图3所示). 目前, CCI噪声已经成为影响MLC闪存可靠性的主要噪声源. CCI噪声影响大小F可用公式(3)计算[3]:
| $F = \mathop \sum \limits_k \left( {\Delta V_{}^{\left( k \right)} \cdot {\gamma ^{\left( k \right)}}} \right)$ | (3) |

|
图 3 CCI干扰示意图 |
其中,
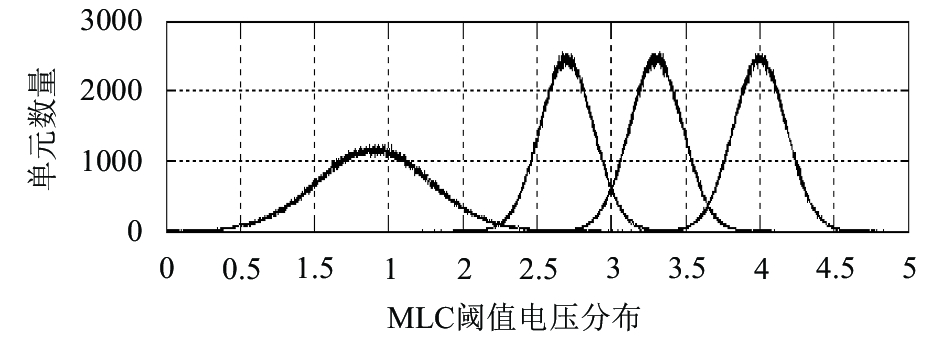
|
图 4 CCI噪声干扰后的MLC阈值电压统计直方图 |
由图4分析可得, MLC闪存在加入CCI噪声后, MLC闪存单元阈值电压发生波动, 相邻的阈值电压分布出现重叠区域, 位于此区域的MLC单元在判决时出错概率较高, 进而导致错误读取存储的数据.
2 MLC闪存的最小和译码算法 2.1 MLC阈值电压的均匀感知和非均匀感知策略读取MLC闪存中存储的信息必须借助阈值电压感知才能得到. 感知方法是通过设定参考电压将每个MLC状态的阈值电压区间进行划分(如图5所示), 将参考电压从小至大加载到被感知单元的控制栅, 根据控制栅的导通性来判断被感知单元的阈值电压是否落入当前参考电压的区间内, 记为

|
图 5 MLC阈值电压均匀感知策略
|
| $\begin{aligned}{L_{{b_0}}} & = {\rm{ln}}\frac{{P\left( {{V_{th}} \in \left[ {{R_l},{R_r}} \right){\rm{|}}{b_0} = 1} \right)}}{{P\left( {{V_{th}} \in \left[ {{R_l},{R_r}} \right){\rm{|}}{b_0} = 0} \right)}}\\& = {\rm{ln}}\frac{{\mathop \sum \nolimits_{l \in \left\{ {0,1} \right\}} P\left( {{V_{th}} \in \left[ {{R_l},{R_r}} \right){\rm{|}}l} \right)}}{{\mathop \sum \nolimits_{l \in \left\{ {2,3} \right\}} P\left( {{V_{th}} \in \left[ {{R_l},{R_r}} \right){\rm{|}}l} \right)}}\\& = {\rm{ln}}\left[ {\frac{{\int_{{R_l}}^{{R_r}} {\{ {p_{{s_0}}}({V_{th}}) + {p_{{s_1}}}({V_{th}})\} d{V_{th}}} }}{{\int_{{R_l}}^{{R_r}} {\{ {p_{{s_2}}}({V_{th}}) + {p_{{s_3}}}({V_{th}})\} d{V_{th}}} }}} \right]\end{aligned}$ | (4) |
| $\begin{aligned}{L_{{b_1}}} & = {\rm{ln}}\frac{{P\left( {{V_{th}} \in \left[ {{R_l},{R_r}} \right){\rm{|}}{b_1} = 1} \right)}}{{P\left( {{V_{th}} \in \left[ {{R_l},{R_r}} \right){\rm{|}}{b_1} = 0} \right)}}\\& = {\rm{ln}}\frac{{\mathop \sum \nolimits_{l \in \left\{ {0,3} \right\}} P\left( {{V_{th}} \in \left[ {{R_l},{R_r}} \right){\rm{|}}l} \right)}}{{\mathop \sum \nolimits_{l \in \left\{ {1,2} \right\}} P\left( {{V_{th}} \in \left[ {{R_l},{R_r}} \right){\rm{|}}l} \right)}}\\& = {\rm{ln}}\left[ {\frac{{\int_{{R_l}}^{{R_r}} {\{ {p_{{s_0}}}({V_{th}}) + {p_{{s_3}}}({V_{th}})\} d{V_{th}}} }}{{\int_{{R_l}}^{{R_r}} {\{ {p_{{s_1}}}({V_{th}}) + {p_{{s_2}}}({V_{th}})\} d{V_{th}}} }}} \right]\end{aligned}$ | (5) |
MLC阈值电压的均匀感知策略(Uniform Sensing Strategy)是对每个状态的阈值电压分布区间进均匀分割进而得到若干个参考电压区间, 图5为感知精度
非均匀感知策略(Non-Uniform Sensing Stra- tegy)动机是若阈值电压处于重叠区域的MLC单元由于判决时不确定性高, 因而需要较高的感知精度, 而处于非重叠区域只需较低感知精度就可保证感知的可靠性. 非均匀感知策略的方法是在相邻阈值电压分布的重叠区间内, 将该区间划分为多个相等的参考区间(如图6所示). 非均匀感知策略可以在保持总体感知精度不变的同时, 提高感知数据的精确度.

|
图 6 MLC阈值电压非均匀感知策略
|
对于非均匀感知策略需要计算MLC阈值电压相邻状态重叠区域的边界. 记第k个
| $\frac{{{p_{{s_k}}}\left( {B_l^{\left( k \right)}} \right)}}{{{p_{{s_{k + 1}}}}\left( {B_l^{\left( k \right)}} \right)}} = \frac{{{p_{{s_{k + 1}}}}\left( {B_r^{\left( k \right)}} \right)}}{{{p_{{s_k}}}\left( {B_r^{\left( k \right)}} \right)}} = R$ | (7) |
为了验证非均匀感知策略的有效性, 在MLC闪存信道下对比均匀感知策略和非均匀感知策略的感知性能. 仿真参数设置为: MLC闪存模型和CCI噪声模型与1.1和1.2节相同, 感知精度p分别使用3, 4, 5和6, 概率比值系数R=512和单元间耦合因子s=1.2下, 统计两种感知策略下RBER.
由图7可以看出, 在MLC闪存单元的阈值电压感知策略中, 使用非均匀感知策略比使用均匀感知策略能够获得更低的RBER, 感知精度为4的非均匀感知策略下的RBER基本等同于感知精度为5的均匀感知策略下的RBER, 减小了感知延迟.

|
图 7 不同感知精度下两种感知策略的性能对比图 |
2.2 MLC闪存的最小和译码算法
和积译码算法是LDPC码的软判决译码算法, 具有较好的译码性能, 但计算复杂度高, 译码时延较大. 最小和译码算法通过简化和积译码算法中校验节点消息更新处理过程, 降低译码算法的计算复杂度, 同时又可以达到同和积译码算法近似的译码效果[10]. 本文采用最小和译码算法作为MLC闪存的纠错码(算法1), 既可保证纠错性能, 又具有较低的译码复杂度, 适用于MLC闪存系统的应用.
3 仿真实验及分析
为了验证这两种感知策略对最小和算法译码性能的影响, 仿真实验使用码率为0.95(34520, 32794)QC-LDPC码, 列重为4, 环长为6, 该码避免了迭代译码过程中出现的短环, 可以提高迭代译码的性能. 设最大迭代次数为20. 仿真使用的单元间干扰耦合因子s∈[0.6,2], 感知精度p取值为3, 4和5, 在MLC阈值电压感知过程中分别使用均匀感知策略(Uniform)和非均匀感知(Non-uniform)策略.
根据图8的仿真结果可以得出, 在MLC闪存模型及相同的CCI噪声作用下, 与均匀感知策略下的最小和译码算法相比, 基于非均匀感知策略的最小和译码算法能够为MLC闪存模型提供更好的纠错性能. 随着MLC阈值电压感知精度的提高, 均匀感知策略和非均匀感知策略下的最小和码算法译码性能都相应提高, 说明感知精度的增加有助于提高LLR值计算的准确性, 进而提高LDPC码的译码性能.

|
图 8 均匀与非均匀感知策略下最小和译码的性能图 |
4 结语
在深入分析MLC闪存模型和CCI噪声的基础上, 由于MLC阈值电压均匀感知策略得到不精确的LLR值会影响LDPC码最小和译码算法译码性能, 因此本文提出一种可以提高LLR计算精度的非均匀阈值电压感知策略, 并将该策略应用到MLC闪存模型中, 通过实验仿真结果表明在相同的感知精度下, 非均匀感知策略比均匀感知策略能够获得更低的原始比特错误率, 而且能提升最小和译码性能, 从而为MLC闪存提供了更高的可靠性保证.
| [1] |
Takeuchi K. NAND flash application and solution. IEEE Solid-State Circuits Magazine, 2013, 5(4): 34-40. DOI:10.1109/MSSC.2013.2278087 |
| [2] |
Klein D. The history of semiconductor memory: From magnetic tape to NAND flash memory. IEEE Solid-State Circuits Magazine, 2016, 8(2): 16-22. DOI:10.1109/MSSC.2016.2548422 |
| [3] |
Dong GQ, Xie ND, Zhang T. On the use of soft-decision error-correction codes in NAND flash memory. IEEE Transactions on Circuits and Systems I: Regular Papers, 2011, 58(2): 429-439. DOI:10.1109/TCSI.2010.2071990 |
| [4] |
Sala F, Immink KAS, Dolecek L. Error control schemes for modern flash memories: Solutions for flash deficiencies. IEEE Consumer Electronics Magazine, 2015, 4(1): 66-73. DOI:10.1109/MCE.2014.2360965 |
| [5] |
Micheloni R, Marelli A, Ravasio R. Error Correction Codes for Non-Volatile Memories. Springer Science & Business Media, 2008: 85–101.
|
| [6] |
Dong GQ, Li S, Zhang T. Using data postcompensation and predistortion to tolerate cell-to-cell interference in MLC NAND flash memory. IEEE Transactions on Circuits and Systems I: Regular Papers, 2010, 57(10): 2718-2728. DOI:10.1109/TCSI.2010.2046966 |
| [7] |
Wang JD, Dong GQ, Courtade T, et al. LDPC decoding with limited-precision soft information in flash memories. arXiv: 1210.0149, 2012: 652–657.
|
| [8] |
Aslam CA, Guan YL, Cai K. Detector for MLC NAND flash memory using neighbor-a-priori information. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2016, 24(9): 2827-2836. DOI:10.1109/TVLSI.2016.2523759 |
| [9] |
Park KT, Kang M, Kim D, et al. A zeroing cell-to-cell interference page architecture with temporary LSB storing and parallel MSB program scheme for MLC NAND flash memories. IEEE Journal of Solid-State Circuits, 2008, 43(4): 919-928. DOI:10.1109/JSSC.2008.917558 |
| [10] |
陈正康, 张会生, 李立欣, 等. LDPC码最小和译码算法的整数量化. 系统工程与电子技术, 2015, 37(10): 2371-2375. DOI:10.3969/j.issn.1001506X.2015.10.28 |
 2018, Vol. 27
2018, Vol. 27


