实现三维场景中目标的尺寸测量的前提是获得目标到达摄像头的距离, 即测距, 而测距分为主动式测距和被动式测距. 主动测距技术主要包括超声波测距、雷达测距、激光测距等, 此测距技术大都需要发射辅助设备. 近年来, 激光雷达传感器因其全方位视角和高分辨率的优点而兴起, 越来越多的被应用于自动驾驶领域, 但其技术垄断, 价格昂贵.
被动式测距中利用视觉信号测距, 相对于激光、雷达和超声波等传感器, 具有探测范围宽、目标信息完整、价格相对便宜, 而且更符合人的认知习惯等优势[1]. 这其中主要包含双目测距[2]和单目测距. 双目测距是基于双目视差的原理, 可实现高精度远距离测距, 特别适用于设备测距、航空目标测距[3]. 双目测距需要用到常见的Tsai的两步法和Zhang的平面法[4]来进行标定求得摄像机内外部参数进行精确的立体匹配[5], 且对于一些特殊约束条件有很高的要求[6], 故其成本高, 计算量大, 技术难度高. 单目视觉测量是其他视觉测量方法的基础[7], 具有可用性更强, 操作简单和成本低等优点. 在单目视觉方法中, 一般采用标定信息获取世界坐标系与图像坐标系间的一一映射关系[4]. 相比于双目测距, 单目测距尽管需要先验的场景信息和几何约束条件, 但仍具有硬件配置和算法更简单的优势.
目前国内外关于单目测距算法的研究大多数应用于车辆和船舶的检测和测距, 单目测距技术有被用来测量智能飞机运动姿态, 测量物体高度, 测量精密元器件[2], 而应用于智能监控领域的很少. 单目测距有基于图像面积变化量的方法和利用针孔模型下的投射几何关系计算的基于交比不变性方法[8,9]; 还有用深度传感器来获取场景的深度信息完成场景的三维重建的方法, Meng Ding等人利用深度传感器完成了人体姿态的跟踪[10]; 另一种常见的方法是将深度感知与模式识别相结合, 并且有实验使用自带图像处理算法的微飞行器验证了该算法[11]. 而近来利用插值思想的三维距离函数测距方法经实验证明简单有效, 但是其受制于限定的平面和特定的静态固定场景, 无法适用于变化多样的应用场景, 且存在误差相对较大的数据结果[12].
1.2 应用场景图1表示的是单摄像头监控下的大范围三维场景画面. 为了获得在此大范围场景下特定目标的大小尺寸, 我们采取了简单快速, 方便有效的单目测量技术. 利用三维距离函数模型来进行平面图像对图片中场景进行三维空间的重建.

|
图 1 单摄像头下的监控场景 |
2 三维场景建模方法 2.1 三维距离函数
图2表示了摄像头成像的几何关系. 凸透镜I为摄像头的简化模型, 其中O是摄像头的光心, OO′为摄像头的光轴, 点A, B是区域的两个顶点, C是AB线上任意一点, A′, B′, C′分别是A, B, C三点的像, O′是光轴OO′与像平面的交点, O′是光心O的像. 三维距离函数是利用摄像头成像的几何原理并采用梅涅劳斯定理, 通过已知AO和BO的距离来求取CO的距离[12].

|
图 2 摄像头成像几何关系图[12] |
2.2 提高三维距离测量精度的方法
图3表示了摄像头成像的立体几何关系. 成像平面简化为面A′B′C′D′, 其中O为摄像头的光心, OO′为与像平面A′B′C′D′垂直的摄像头光轴, 面ABCD是监控区域. 其中, AB是区域的一条边界线. 在图2中我们可以看出, 在一个实际的投射面OAB (面OA′B′)上, 三维距离函数的计算需要用到OO′[11], 图2中的OO′的物理意义应为图3中摄像机光轴OO′在投射面上的投影. 图3中, OO″的值随着监控区域投射面的位置变化而变化, 本文选择OO″作为轴线进行计算, 从而提高了三维距离函数测量的精度.

|
图 3 摄像头成像立体几何关系图 |
2.3 场景标记
针对一般监控(单摄像头俯拍角度)拍摄的画面, 我们需要对监控视图进行三维立体建模. 首先我们标记出视图中地面区域, 图4中用多边形ABCDEFGHI表示.

|
图 4 监控视野水平面图 |
接下来对与地面垂直的建筑物进行标定, 这里我们选取了AINM面作为实验面, 选取场景中的行人为实验目标, 选取行人身高高度为尺寸测量参数. 至此, 监控视图下的三维空间标记已经完成.
2.4 三维立体空间的距离我们事先已知边界角点到摄像头的距离, 并通过相邻边界角点来计算此边界上任意一点到摄像头的距离, 进而利用边界点求取边界围成的区域内任一点到摄像头的距离. 故运用改进的三维距离函数我们可以依次计算出ABCDEFGHI边界上的任一点的距离, 从而计算出ABCDEFGHI平面内任一点的距离[11].
3 扩大测量范围的方法 3.1 垂直面测量函数通过三维场景建模我们求得图4中ABCDEFGHI平面内任一点到摄像头的距离, 接下来求解图5中垂直面AINM面内任一点到摄像头的距离. 在图6中, 我们构造垂直面成像几何关系图, 其中O为摄像头的光心, OO′为光轴在投射面上的投影, I′N′为垂直面, OA′为摄像头到垂直面的距离, OD为摄像头到水平面的距离为d.

|
图 5 监控视野垂直面图 |

|
图 6 垂直面成像几何关系图 |
求解垂直面内任一点到摄像头距离M′O过程如下:
| $|OA'| = \sqrt {|OI'{|^2} - |OD{|^2}} $ | (1) |
| $\angle I'OD = \arcsin (\frac{{|OA'|}}{{|OI'|}})$ | (2) |
| $|OI''| = \sqrt {|OO'{|^2} + |O'I''{|^2}} $ | (3) |
| $|OQ| = |OI''| \cdot \sin \angle I'OD$ | (4) |
| $|I''Q| = |OI''| \cdot \cos \angle I'OD$ | (5) |
| $|I''A''| = \frac{{|I''Q|}}{{\cos \angle QI''A''}}$ | (6) |
| $|A''Q| = |I''A''| \cdot \sin \angle QI''A''$ | (7) |
| $|OA''| = |A''Q| + |OQ|$ | (8) |
| $\cos \angle M''OA'' = \frac{{|OM''{|^2} + |OA''{|^2} - |M''A''{|^2}}}{{2 \cdot |OM''| \cdot |OA''|}}$ | (9) |
| $|M'O| = \frac{{|OA'|}}{{\cos \angle M''OA''}}$ | (10) |
| $|M'I'| = |OD| - \sqrt {|M'O{|^2} - |OA'{|^2}} $ | (11) |
其中M′I为垂直面内任一点到地面的垂直距离. 至此三维空间视野内任一平面内点到摄像头的距离即已知.
垂直面上任意两点的距离:
| $|M'A'| = \sqrt {|OM'{|^2} - |OA{|^2}} $ | (12) |
| $|N'A'| = \sqrt {|ON'{|^2} - |OA{|^2}} $ | (13) |
| $|M'N'| = |M'A'| + |N'A'|$ | (14) |
至此, 我们可以求得垂直面上任意两点之间的距离, 实现了垂直面上的尺寸测量. 针对传统三维距离函数模型中测量目标部分跳出监控区域地面的情况, 本文在此基础上进一步提出了水平垂直联合检测函数.
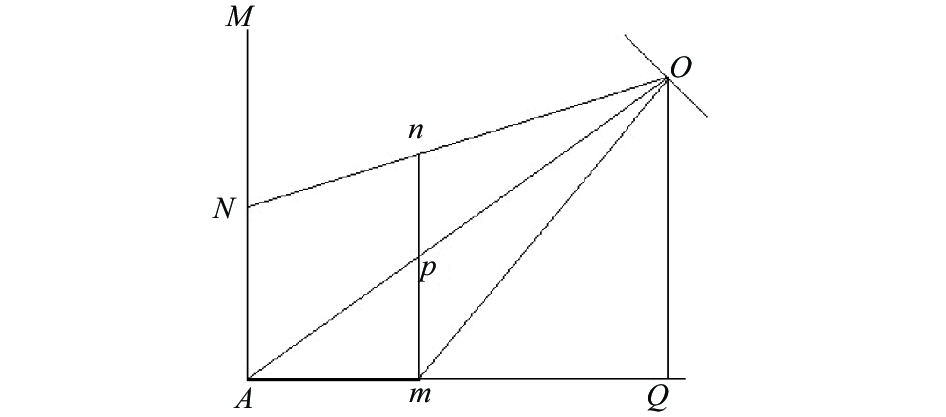
3.2 水平垂直联合测量函数图7中, AQ为地面, MA为与垂直面, O为摄像头的光心, mn为待测目标. 当地面上的目标部分超出了图4中预设的ABCDEFGHI面时, 我们将目标mn分为mp和np分别测量. mp部分利用传统三维距离函数模型即可求[11].
|
图 7 水平垂直联合检测 |
np部分的求解: 由垂直面测量部分已知|AN|, |mO|, |AO|, |NO|.
| $|mQ| = \sqrt {|mO{|^2} - |OQ{|^2}} $ | (15) |
| $|AQ| = \sqrt {|AO{|^2} - |OQ{|^2}} $ | (16) |
| $|np| = \frac{{|mQ|}}{{|AQ|}} \cdot |NA|$ | (17) |
| $|mn| = |np| + |mp|$ | (18) |
至此, 我们实现了地面、垂直面的单独尺寸测量和水平垂直联合测量.
4 实验内容与分析 4.1 优化后三维距离函数实验本实验选取了在摄像头监测区域的水平地面上均匀分布的8个点, 光轴OO′距离分别取3.8 mm、4.0 mm、4.2 mm和4.4 mm, 通过优化后的三维环境距离函数获得八组距离值. 表1表示了测量距离与实际距离的对比.
| 表 1 目标距离测量表(单位: mm) |
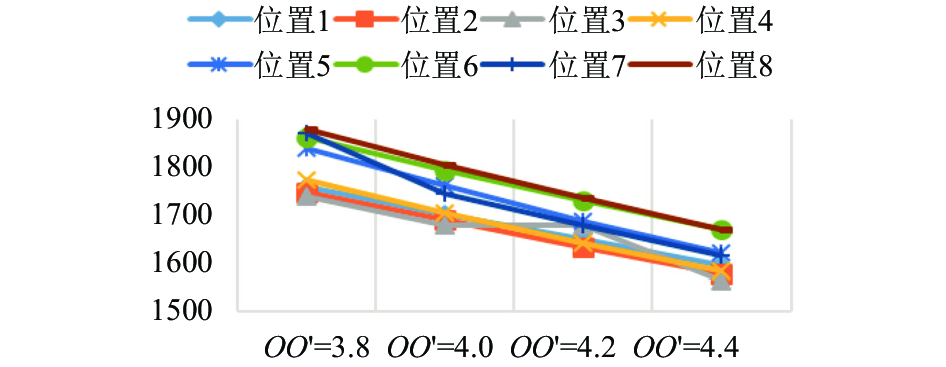
4.2 水平面行人高度测量实验
本实验同样选取了在摄像头监测区域的地面上均匀分布的8个点, 即为表1中测距时的8个点. 光轴OO′距离也分别取3.8 mm、4.0 mm、4.2 mm和4.4 mm. 表2表示了同一个人被测量的高度与实际高度的对比.
| 表 2 目标身高测量表(单位: mm) |
4.3 垂直面测量实验
本实验分别选取了在摄像头监测区域图4中AINM面上的目标门(位置1), 黄牌(位置2), 白牌(位置3), 光轴OO′距离分别取3.8 mm、4.0 mm、4.2 mm和4.4 mm. 通过垂直面测量函数分别获取目标的尺寸. 表3表示了垂直面上测量尺寸与实际尺寸的对比.
| 表 3 垂直面尺寸测量表(单位: mm) |
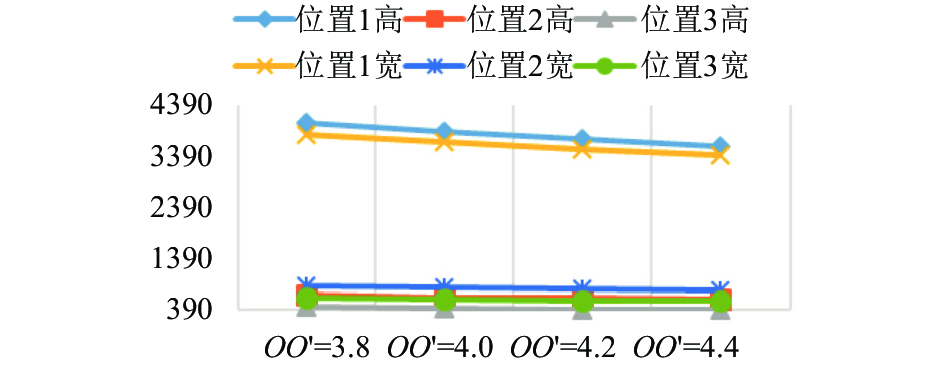
4.4 水平垂直面联合检测实验
本实验选取了在摄像头监测区域内, 目标同时出现在面AINM和面ABCI的情况, 光轴OO′距离分别取3.8 mm、4.0 mm、4.2 mm和4.4 mm. 因为通过4.1, 4.2, 4.3的实验基础, 这里我们只选取了两个位置. 通过水平垂直联合测量函数分别获取目标的高度. 表4表示了联合检测时测量高度与实际高度的对比.
| 表 4 联合高度测量表(单位: mm) |
4.5 实验数据分析
通过实验数据, 我们做出图8至图11, 当光轴OO′距离分别取3.8 mm、4.0 mm、4.2 mm和4.4 mm时, 测量数据与实际数据都存在一定误差, 本文采用(
综上, 我们可以发现, 当光轴OO′距离取4.2 mm时, 四项实验的平均相对误差都较小. 此时距离平均误差为0.9%, 相比于双目摄像的测距系统不到3%[13]的平均误差、基于小孔模型的单目测距中的未校正误差2%–4%[6]和传统三维距离函数模型下2.3%[12]的平均误差都有了一定程度上的降低. 而此时身高部分的三组实验平均误差分别为2.0%、1.2%、0.4%, 与传统三维距离函数模型下1.74%的平均误差基本持平并有下降趋势.

|
图 8 目标距离测量折线图 |
|
图 9 水平面目标高度折线图 |

|
图 10 垂直面尺寸测量折线图 |
|
图 11 联合检测高度折线图 |
5 实验结论
本文提出一种三维场景建模的方法, 修改了三维距离函数中光轴参数OO′的选择过程, 而且针对原有三维距离函数存在的空间局限性问题提出了扩大测量范围的方法. 经实验数据分析证明, 此方法简单有效地实现了固定单摄像头下三维场景的目标尺寸测量, 扩大了测量范围、提高了测量精度.
| [1] |
周欣, 黄席樾, 黎昱. 基于单目视觉的高速公路车道保持与距离测量. 中国图像图形学报, 2003, 8(5): 590-595. |
| [2] |
姜雨彤, 杨进华, 刘钊, 等. 双目CCD测距系统的高精度标定. 计算机工程, 2013, 39(7): 228-232. |
| [3] |
李春艳, 王立, 卢欣, 等. 一种双目立体视觉相机标定方法. 空间控制技术与应用, 2010, 36(3): 51-54. |
| [4] |
Zhang ZY. A flexible new technique for camera calibration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. DOI:10.1109/34.888718 |
| [5] |
Wahab MNA, Sivadev N, Sundaraj K. Development of monocular vision system for depth estimation in mobile robot-robot soccer. 2011 IEEE Conference on Sustainable Utilization and Development in Engineering and Technology (STUDENT). Semenyih, Malaysia. 2011. 36–41.
|
| [6] |
王士明. 基于计算机视觉的车辆单目测距系统研究[硕士学位论文]. 天津: 天津大学, 2012.
|
| [7] |
李强. 单目视觉实时测距算法研究[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2014.
|
| [8] |
Wang SM, Fan YL. A vision location algorithm for CCD camera based on geometric knowledge. 2nd International Conference on Environmental Science and Information Application Technology. Wuhan, China. 2010. 430–433.
|
| [9] |
朱梦哲, 冯瑞. 基于三维模型的粒子滤波行人跟踪算法. 计算机系统应用, 2016, 25(11): 112-117. DOI:10.15888/j.cnki.csa.005420 |
| [10] |
Ding M, Fan GL. Generalized sum of Gaussians for real-time human pose tracking from a single depth sensor. 2015 IEEE Winter Conference on Applications of Computer Vision (WACV). Waikoloa, HI, USA. 2015. 47–54.
|
| [11] |
Celik K, Chung SJ, Clausman M, et al. Monocular vision SLAM for indoor aerial vehicles. The 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. St. Louis, MO, USA. 2009. 1566–1573.
|
| [12] |
钱娜. 基于三维距离函数的视频多目标检测与跟踪研究[硕士学位论文]. 济南: 济南大学, 2009.
|
| [13] |
李千, 尹业安. 基于双目摄像的测距系统及立体匹配算法研究. 通信电源技术, 2016, 33(2): 66-67. |
 2018, Vol. 27
2018, Vol. 27



