红外与可见光图像融合在公共安全方面均有广泛的应用, 特别是在国家和社会安全监控等民用领域^[1]. 图像融合评估有助于研究人员设计出更为科学、精度更高的图像融合方法. 图像融合质量评价分为主观评价和客观评价^[2]. 主观评价是由观察者的主观感觉和统计结果对融合图像的优劣做出主观定性评价. 例如, Petrovixc^[3]建立一个包含120组图像的数据集, 其中110组为遥感图像融合, 6组为红外与可见光融合, 4组为可见光与可见光图像融合, 每组图像包含2幅源图像和2幅融合图像, 并提供组内两幅融合图像获得的投票数, 客观评价采用数学公式定量评价图像融合质量. 常用的客观评价指标有很多种, 大致分为四类: 1)基于统计特性的评价指标; 2)基于信息论的评价指标; 3)基于结构相似度的评价指标; 4)基于人眼视觉系统的评价指标.

张小利等人^[4]在Petrovixc图像融合数据库的基础上, 研究了评价指标的正确率排名, 结果表明: 大部分评价指标的正确率排名均小于0.8, 故单个评价指标很难完成准确评估融合质量的任务, 需要进行综合评价. 因此面临的主要问题在于: 所选的评价指标必须满足非冗余性原则. 虽然文献[4]研究了融合图像质量评价指标的相关性, 但结合红外与可见光图像融合质量评价, 该研究存在以下不足: 1) Petrovixc图像融合主观数据库中遥感图像的个数占91.7%, 文献[4]侧重分析遥感图像图像融合质量评价指标的相关性; 2) 文献[4]采用的融合方法比较陈旧, 已经无法满足现阶段融合方法质量评价的需求; 3) 文献[4]采用阈值分类对评价指标进行聚类分析, 所选阈值具有随机性, 无法保证分类的有效性.

借鉴文献[4]总结的融合图像质量评价指标, 本文从斯皮尔曼等级相关系数和灰色关联分析理论研究评价指标在红外与可见光图像融合质量评价的相关性.

1 客观评价指标

根据图像融合质量评价原理, 将图像融合质量评价方法分为4类: 基于统计特性的评价指标、基于信息论的评价指标、基于结构相似度的评价指标、基于人眼视觉系统的评价指标.

设A, B分别表示两源图像, 采用融合算法将两源图像进行融合, 得到融合图像F, 图像的大小均为M×N, 图像中的灰度级数为L.

1.1 基于统计特性评价指标

本文主要介绍常用的统计特性评价指标, 包括: 平均梯度(Average Gradient, AG)、空间频率(Spatial Frequency, SF)、均方误差(Mean Square Error, MSE)、峰值信噪比(peak signal to noise ratio, PSNR)、相关系数(Correlation Coefficient, CC). 其中, AG反映图像微小细节变化与纹理变化的反差特征, SF反映图像灰度的变化率, MSE反映变量之间的差异, PSNR衡量有效信息与噪声之间的比率, CC衡量变量间相关关系密切的程度. 上述评价指标的计算公式详见文献[4].

1.2 基于信息论的评价指标

信息熵作为图像融合质量评价指标, 用于衡量融合图像信息丰富程度. 但该指标只是衡量了融合图像自身的信息量, 无法衡量源图像传递给融合图像的信息量, 评价结果具有片面性. 互信息用于衡量融合图像保留源图像信息量的多少, 较为准确地反映图像融合质量. 故本文介绍源图像与融合图像间的互信息及其改进算法.

(1) 互信息

对于图像X, Y, 它们间的互信息计算公式如下:

${I_{X,Y}} = \sum\limits_{x,y} {{p_{XY}}\left( {x,y} \right){{\log }_2}\frac{{{p_{XY}}\left( {x,y} \right)}}{{{p_X}\left( x \right){p_Y}\left( y \right)}}} $

式中, ${p_{XY}}\left( {x,y} \right)$ 是图像X, Y间的归一化联合灰度直方图, ${p_X}\left( x \right)$ 和 ${p_Y}\left( y \right)$ 分别为图像X, Y的概率密度分布.

在已知源图像A, B和融合图像F的基础上, 基于互信息的融合质量评价指标计算公式如下:

$M_{A,B}^F = {I_{F,A}} + {I_{F,B}}$

融合图像的互信息越大, 融合图像质量越优, 反之, 则融合图像质量越差.

(2) Taillis熵

Cvejic^[5]利用Taillis熵改进了互信息, 其计算公式如下所示:

$M_{F,A,B}^\alpha = I_{F,A}^\alpha + I_{_{F,B}}^\alpha $

这里,

$I_{F,A}^\alpha \left( {f,a} \right) = \frac{1}{{1 - \alpha }}\left( {1 - \sum\limits_{f,a} {\frac{{{{\left( {{p_{F,A}}\left( {f,a} \right)} \right)}^\alpha }}}{{{{\left( {{p_F}\left( {f,a} \right){p_A}\left( a \right)} \right)}^{\alpha - 1}}}}} } \right)$

$I_{F,B}^\alpha \left( {f,b} \right) = \frac{1}{{1 - \alpha }}\left( {1 - \sum\limits_{f,b} {\frac{{{{\left( {{p_{F,B}}\left( {f,b} \right)} \right)}^\alpha }}}{{{{\left( {{p_F}\left( {f,a} \right){p_B}\left( b \right)} \right)}^{\alpha - 1}}}}} } \right)$

融合图像的Taillis熵越大, 则融合图像质量越优, 反之, 则融合图像质量越差.

1.3 基于结构相似度的图像融合评估指标

结构相似度理论是一种关于图像质量评价的新思想. 它自顶向下地模拟HVS整体功能, 使得测量结构信息的改变与感知图像质量的变化非常接近. 图像X, Y间的结构相似度表达式如下:

$SSIM\left( {X,Y} \right) \! = \! \frac{{2{\mu _X}{\mu _Y} \! + \! {C_1}}}{{\mu _X^2 + \mu _Y^2 \! + \! {C_1}}}\frac{{2{\sigma _X}{\sigma _Y} \! + \! {C_2}}}{{\sigma _X^2 \! + \! \sigma _Y^2 \! + \! {C_2}}}\frac{{2{\sigma _{XY}} \! + \! {C_3}}}{{{\sigma _X}{\sigma _Y} \! + \! {C_3}}}$

这里, ${\mu _X},{\mu _Y},{\sigma _X},{\sigma _Y}$ 分别为图像X, Y的均值和标准差, ${\sigma _{XY}}$ 是图像X, Y的协方差, ${C_1},{C_2},{C_3}$ 为常数.

在此基础上, Piealla^[6]提出了三个融合图像质量评价指标: $Q,{Q_w},{Q_E}$ . 融合图像的评价指标 $Q,{Q_w},{Q_E}$ 值越大, 表明融合图像质量越优; 反之, 则评价指标质量越差.

下面对三个指标进行描述:

(1) 评价指标Q

评价指标Q的计算思想: 首先分别计算融合图像F和源图像A, B在局部窗口w内的结构相似度SSIM $\left( {A,F|w} \right)$ 和 $SSIM\left( {B,F|w} \right)$ ; 然后利用输入图像的局部显著度构成归一化局部权重系数 $\lambda \left( w \right)$ , 表示源图像之间的相对重要程度; 最后通过加权乘法获得融合图像质量. 其表达式如式(1).

$\begin{split}Q\left( {A,B,F} \right) & = \; \frac{1}{{\left| W \right|}}\sum\limits_{w \in W} {\lambda \left( w \right)SSIM\left( {A,F|w} \right) } \\&+ \left( {1 - \lambda \left( w \right)} \right)SSIM\left( {B,F|w} \right)\end{split}$

(1)

其中, $\left| W \right|$ 是W的基数. $\lambda \left( w \right)$ 是源图像的局部显著度构成的归一化权重, 其表达式如下:

$\lambda \left( w \right) = \frac{{s\left( {A|w} \right)}}{{s\left( {A|w} \right) + s\left( {B|w} \right)}}$

这里, $s\left( {A|w} \right),s\left( {B|w} \right)$ 分别表示图像A, B在窗口w的显著性.

(2) 评价指标Q_w

Piella考虑到窗口重要性不同, 对式(1)进行改进, 得到加权结构相似度 ${Q_w}\left( {A,B,F} \right)$ :

$\begin{split}{Q_w}\left( {A,B,F} \right)& = \; \sum\limits_{w \in W} {c\left( w \right)} \left[ {\lambda \left( w \right)SSIM\left( {A,F|w} \right) } \right.\\& + \left. {\left( {1 - \lambda \left( w \right)} \right)SSIM\left( {B,F|w} \right)} \right]\end{split}$

其中, $c\left( w \right)$ 是图像块w在整个图像中的重要程度:

$c\left( w \right) = \frac{{C\left( w \right)}}{{\sum\limits_{w’ \in W} {C\left( {w’} \right)} }},C\left( w \right) = \max \left\{ {s\left( {A|w} \right),s\left( {B|w} \right)} \right\}。$

(3) 评价指标Q_E

考虑到图像质量优劣与边缘的完整度、清晰度有关, Piella在获得评价指标 ${Q_w}\left( {A,B,F} \right)$ 的基础上, 分别获取源图像和融合图像的边缘图像 $A’,B’,F’$ , 然后求出 ${Q_w}\left( {A’,B’,F’} \right)$ , 得到基于边缘结构相似指标Q_E:

${Q_E} = {Q_w}{\left( {A,B,F} \right)^{1 - \alpha }} + {Q_w}{\left( {A’,B’,F’} \right)^\alpha }$

1.4 基于人眼视觉系统的评价指标

基于人眼视觉系统的评价指标是模仿人眼对像素层绝对差值的认知机制, 通过掩盖低于人眼感知能力的差异修正评测结果. 该类指标主要被划分为2部分: 1)基于显著性几何评价指标; 2)基于边缘保持度的评价指标.

1.4.1 基于显著性几何评价指标

Luo等人^[7]利用图像区域显著性对结构相似度进行改进, 提出了基于显著性几何评价指标. 该指标的计算过程如下:

首先, 分别计算源图像A, B的显著性, 将所得结果存入到 ${S_A},{S_B}$ 中, 当源图像A, B在点 $\left( {x,y} \right)$ 处的显著性大于阈值t, 则认为此处是显著性位置; 否则, 则认为是非显著性位置.

然后, 分别统计源图像A, B与融合图像F在显著性区域、非显著性区域的相似度. 以源图像A和融合图像F为例, 计算方法如下所示:

$\begin{array}{l}{S_{SSIM}}\left( {F,A} \right) = \frac{1}{{{m_1}}}\sum\limits_{{S_{A\left( {x,y} \right) \ge t}}} {\left| {SSI{M_{FA}}\left( {x,y} \right)} \right|} \\{L_{SSIM}}\left( {F,A} \right) = \frac{1}{{{m_2}}}\sum\limits_{{S_{A\left( {x,y} \right) < t}}} {\left| {SSI{M_{FA}}\left( {x,y} \right)} \right|} \end{array}$

式中, ${m_1},{m_2}$ 分别表示显著性区域、非显著区域中像素的个数.

其次, 将它们进行整合, 得到源图像A和融合图像F的整体相似度为:

$FIQRO\left( {F,A} \right) = {\left[ {{S_{SSIM}}\left( {F,A} \right)} \right]^\alpha }{\left[ {{L_{SSIM}}\left( {F,A} \right)} \right]^{1 - \alpha }}$

同样, 获得源图像B和融合图像F的整体相似度 $FIQRO\left( {F,B} \right)$ .

结合 $FIQRO\left( {F,A} \right)$ 和 $FIQRO\left( {F,B} \right)$ , 基于显著性几何评价指标表达式为:

$FIFQ = 1 - \sqrt {\frac{{{{\left( {{a_1} - FIQRO\left( {F,A} \right)} \right)}^2} + {{\left( {{a_2} - FIQRO\left( {F,B} \right)} \right)}^2}}}{2}} $

其中, ${a_1},{a_2}$ 为参数, 通常取 ${a_1} = {a_2} = 1$ .

1.4.2 基于边缘保持度的评价指标

根据视觉系统特性, Xydeas等人^[8]提出了一种衡量边缘信息量从源图像到融合图像多少的客观评价指标. 其实质是通过Sobel算子分别计算输入、输出图像的边缘信息, 得到边缘信息传递的量化值, 然后对源图像的边缘保持度加权求和得到最终值. 其计算步骤如下:

Step 1. 计算源图像A, B到融合图像F的边缘信息保留值 ${Q_{AF}}\left( {x,y} \right)$ 和 ${Q_{BF}}\left( {x,y} \right)$ .

以 ${Q_{AF}}\left( {x,y} \right)$ 的计算过程为例进行说明.

首先, 应用式(2)计算源图像A和融合图像F在点 $\left( {x,y} \right)$ 处的边缘强度 ${g_A}\left( {x,y} \right)$ 和 ${g_F}\left( {x,y} \right)$ :

$\left\{ {\begin{array}{l}{g_A}\left( {x,y} \right) = \sqrt {S_x^A{{\left( {x,y} \right)}^2} + S_x^A{{\left( {x,y} \right)}^2}} \\{g_F}\left( {x,y} \right) = \sqrt {S_x^F{{\left( {x,y} \right)}^2} + S_x^F{{\left( {x,y} \right)}^2}} \end{array}}\right.$

(2)

其中, $S_x^A\left( {x,y} \right),S_y^A\left( {x,y} \right)$ 分别为应用Sobel算子对源图像A进行x方向和y方向滤波的结果.

再应用式(3)计算源图像A和图像F在点 $\left( {x,y} \right)$ 处的边缘方向 ${\alpha _A}\left( {x,y} \right),{\alpha _F}\left( {x,y} \right)$ :

$\left\{ {\begin{aligned}{\alpha _A}\left( {x,y} \right) = \arctan \frac{{S_y^A\left( {x,y} \right)}}{{S_x^A\left( {x,y} \right)}}\\{\alpha _F}\left( {x,y} \right) = \arctan \frac{{S_y^F\left( {x,y} \right)}}{{S_x^F\left( {x,y} \right)}}\end{aligned}}\right.$

(3)

然后, 应用式(4)计算源图像A相对于融合图像F的相对边缘强度 ${G_{AF}}\left( {x,y} \right)$ 和边缘方向 ${A_{AF}}\left( {x,y} \right)$ :

$\left\{ {\begin{aligned} {G_{AF}}\left( {x,y} \right) & = \left\{ \begin{aligned} & \frac{{{g_F}\left( {x,y} \right)}}{{{g_A}\left( {x,y} \right)}}, \;\;\;\;if \;\;{g_A}\left( {x,y} \right) > {g_F}\left( {x,y} \right) \\ & \frac{{{g_A}\left( {x,y} \right)}}{{{g_F}\left( {x,y} \right)}}, \;\;\;\;otherwise \end{aligned} \right.\\ {A_{AF}}\left( {x,y} \right) & = \frac{{\left| {\left| {{\alpha _A}\left( {x,y} \right) - {\alpha _F}\left( {x,y} \right)} \right| - \pi /2} \right|}}{{\pi /2}} \end{aligned}}\right.$

(4)

应用式(5)得到源图像A到融合图像F的边缘信息保留值 ${Q_{AF}}\left( {x,y} \right)$ :

$\begin{aligned}{Q_{AF}}\left( {x,y} \right) & = Q_g^{AF}\left( {x,y} \right)Q_\alpha ^{AF}\left( {x,y} \right)\\& = \frac{{{\Gamma _g}}}{{1 + {e^{{k_g}\left( {{G_{AF}}\left( {x,y} \right) - {\sigma _g}} \right)}}}}\frac{{{\Gamma _\alpha }}}{{1 + {e^{{k_\alpha }\left( {{A_{AF}}\left( {x,y} \right) - {\sigma _\alpha }} \right)}}}}\end{aligned}$

(5)

其中, ${\Gamma _g},{k_g},{\sigma _g},{\Gamma _\alpha },{k_\alpha },{\sigma _\alpha }$ 均为常量.

同样, 应用式(2)至式(5)得到源图像B到融合图像F的边缘信息保留值 ${Q_{BF}}\left( {x,y} \right)$ .

Step 2. 计算基于边缘保持度的质量评价指标 ${Q_{AB/F}}$ .

${Q_{AB/F}} = \frac{{\sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {\left( {{Q_{AF}}\left( {x,y} \right){\omega _A}\left( {x,y} \right) + {Q_{BF}}\left( {x,y} \right){\omega _B}\left( {x,y} \right)} \right)} } }}{{\sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {\left( {{\omega _A}\left( {x,y} \right) + {\omega _B}\left( {x,y} \right)} \right)} } }}$

(6)

这里, ${\omega _A}\left( {x,y} \right)$ 和 ${\omega _B}\left( {x,y} \right)$ 分别是源图像A, B的边缘强度, 其表达式分别为:

${\omega _A}\left( {x,y} \right){\rm{ = }}{\left( {{g_A}\left( {x,y} \right)} \right)^L},\;\;{\omega _B}\left( {x,y} \right){\rm{ = }}{\left( {{g_B}\left( {x,y} \right)} \right)^L}$

式中, L是常数.

Xydeas等人^[9]在进一步考虑人眼视觉感知性能后, 通过对融合图像与源图像之间各像素点上的边缘强度添加阈值T_g和计算各邻域内像素方向的一致性程度来分辨融合图像中出现的噪声和边缘情况, 在此基础上, 改进了加权系数 ${\omega _A}\left( {x,y} \right)$ 和 ${\omega _B}\left( {x,y} \right)$ , 具体表达式见式(7).

$\left\{ {\begin{aligned}{\omega _A}\left( {x,y} \right) = \left\{ \begin{array}{l}\omega _{\min }^A,\begin{array}{*{20}{c}}{}&{}&{}&{}&{}\end{array}{g_A}\left( {x,y} \right) \le {T_g}\\{g_A}\left( {x,y} \right) \times {c_A}\left( {x,y} \right),{g_A}\left( {x,y} \right) > {T_g}\end{array} \right.\\{\omega _B}\left( {x,y} \right) = \left\{ \begin{array}{l}\omega _{\min }^B,\begin{array}{*{20}{c}}{}&{}&{}&{}&{}\end{array}{g_B}\left( {x,y} \right) \le {T_g}\\{g_B}\left( {x,y} \right) \times {c_B}\left( {x,y} \right),{g_B}\left( {x,y} \right) > {T_g}\end{array} \right.\end{aligned}}\right.$

(7)

式中, ${c_A}\left( {x,y} \right)$ 和 ${c_B}\left( {x,y} \right)$ 表示图像A, B邻域内像素方向一致性程度. 为方便起见, 均记为 $c\left( {x,y} \right)$ , 表达式如式(8).

$c\left( {x,y} \right) = \frac{{\sum\limits_{\left( {x{\rm{*}},y{\rm{*}}} \right) \in W{\rm{*}}} {g\left( {x{\rm{*}},y{\rm{*}}} \right)} }}{{\sum\limits_{\left( {x{\rm{*}},y{\rm{*}}} \right) \in W} {g\left( {x{\rm{*}},y{\rm{*}}} \right)} }}$

(8)

这里, W是中心处在 $\left( {x,y} \right)$ , 且大小为 $k \times l$ 的窗口, 窗口 $W*{\rm{ = }}W \cap \left[ {\alpha \left( {x,y} \right) - \delta ,\alpha \left( {x,y} \right) + \delta } \right]$ , $\delta $ 为常数.

将新的权重系数 ${\omega _A}\left( {x,y} \right)$ 和 ${\omega _B}\left( {x,y} \right)$ 代入式(6), 获得基于改进的边缘保持度图像融合质量评价指标.

2 相关性指标

本文采用斯皮尔曼等级相关系数和灰色关联理论分析图像融合质量评价指标在红外与可见光图像融合中的相关性.

2.1 基于灰色关联度的相关性分析

灰色系统理论对样本数据量的要求不高、设计思路相对简单, 能够解决因统计资料不足而造成的信息不完善的问题. 灰色关联分析理论是灰色系统理论的重要组成部分, 它通过各个样本序列的曲线几何形状的相似度来判断序列之间的关系.

向量 $x = {\left( {{x_i}} \right)_{1 \times N}}$ 和 $y = {\left( {{y_i}} \right)_{1 \times N}}$ 间的灰色绝对关联度表达式如式(9).

${r_{xy}} = \frac{1}{{N{\rm{ - }}1}}\sum\limits_{i = 1}^{N{\rm{ - }}1} {\frac{1}{{1{\rm{ + }}\left| {\left( {{x_{i + 1}} - {x_i}} \right) - \left( {{y_{i + 1}} - {y_i}} \right)} \right|}}} $

(9)

2.2 斯皮尔曼相关系数

设两变量X和Y, 它们的长度均为N. X和Y均按降序排列后分别记为X_sort和Y_sort. X’和Y’分别记录X和Y中元素在X_sort和Y_sort中的位置, 并称其为秩次. 记 ${d_i} = X’\left( i \right) - Y’\left( i \right)$ , 斯皮尔曼相关系数 ${\rho _s}$ 表示为式(10).

${\rho_s} = 1 - \frac{{6\sum\limits_{i = 1}^N {d_i^2} }}{{N\left( {{N^2} - 1} \right)}}$

(10)

${\rho _s}$ 反映客观评价指标的单调性, ${\rho _s} \in \left[ { - 1,1} \right]$ . 当 ${\rho _s} = 1$ 时, 表示X和Y秩次完全相同; 当 ${\rho _s} = - 1$ 时, 表示X和Y的秩次完全相反; 当 ${\rho _s} = 0$ 时, X和Y不相关. 当 ${\rho _s}$ 越接近1, 表明客观评价指标单调性越好.

2.3 选取聚类阈值

通过计算两两评价指标间的相关度得到对角线为1的相关矩阵 $R = {\left( {{r_{ij}}} \right)_{N \times N}}$ . 将R中除了对角线元素以外的所有互不相同的元素按照从大到小的顺序编排, 表示为:

$1 = {\theta _1} > {\theta _2} > {\theta _3} > \cdots $

(11)

取阈值 $\theta = {\theta _k}$ , 当 ${r_{ij}} \ge {\theta _k}\left( {i \ne j} \right)$ , 则认为指标u_i和指标u_j具有相同特性并将其分为一类.

设 ${B_1},{B_2}$ 是聚类阈值为 ${\theta _k}$ 时的两个类, 若 ${B_1} \cap {B_2} \ne \emptyset $ , 称它们是相似的, 将所有相似的类合并成一个类, 最后得到的分类就是阈值 ${\theta _k}$ 时的等价分类.

Zhang^[10]采用 $\theta $ 的变化率C_i确定聚类阈值 $\theta $ :

${C_i} = \frac{{{\theta _{i - 1}} - {\theta _i}}}{{{n_i} - {n_{i - 1}}}}$

(12)

其中, i为 $\theta $ 从大到小的聚类次数, n_i和 ${n_{i - 1}}$ 分别为第i次和第 $i - 1$ 次聚类的对象个数, ${\theta _i}$ 和 ${\theta _{i - 1}}$ 分别为第i次和第 $i - 1$ 次聚类时的阈值, 若

${C_i} = \mathop {\max }\limits_j \left( {{C_j}} \right)$

(13)

则认为第i次聚类对应阈值为最优聚类阈值.

从公式(12)可以看出: 阈值θ的变化率C_i越大, 表明类别之间的差异越大, 类与类之间的边界就越明显. 因此, 取最大C_i对应的θ_i为最优聚类阈值.

3 融合图像质量评价指标相关性分析

实验图像来源于美国麻省理工学院林肯实验室、荷兰人力资源研究所、美国海军研究生院在网络上提供的红外与可见光源图像, 共计10组图像, 见图1.

本文采用融合方法包括: 基于奇异值分解的PCNN融合方法^[11]、基于Tetrolet变换的融合方法^[12]、基于非下采样Contourlet变换和稀疏表示的融合方法^[13]、基于对比度增强的融合方法^[14]、基于多特征的融合方法^[15]和基于剪切波变换的图像融合方法^[16]. 上述融合方法既具有代表性, 且融合效果比较好. 由于篇幅限制, 图2给出了第七组源图像及其融合图像.

采用的评价指标有: 峰值信噪比 $\left( {{u_1}} \right)$ 、显著性几何评价指标VIFF $\left( {{u_2}} \right)$ 、平均梯度 $\left( {{u_3}} \right)$ 、指标Q $\left( {{u_4}} \right)$ 、互信息 $\left( {{u_5}} \right)$ 、指标Q_w $\left( {{u_6}} \right)$ 、边缘保持度Q_AB/F $\left( {{u_7}} \right)$ 、指标Q_E $\left( {{u_8}} \right)$ 、Taillis熵 $\left( {{u_9}} \right)$ 、空间频率 $\left( {{u_10}} \right)$ 、相关系数 $\left( {{u_11}} \right)$ .

3.1 评价指标规范化处理

图像融合质量评价指标的物理意义和计量单位不相同, 在对融合图像质量评价指标进行相关性分析时, 需要对评价指标进行规范化处理. 根据评价指标与融合图像质量的关系, 除了均方误差属于“越小越优型”外, 其它评价指标均属于“越大越优型”. 本文采用公式(14)对评价指标值进行规范化处理.

${x_{ij}} = \left\{ \begin{array}{l}\frac{{{x_{ij}} - \mathop {\min }\limits_i \left\{ {{x_{ij}}} \right\}}}{{\mathop {\max }\limits_i \left\{ {{x_{ij}}} \right\} - \mathop {\min }\limits_i \left\{ {{x_{ij}}} \right\}}},{u_j} \in {T_1}\\\frac{{\mathop {\max }\limits_i \left\{ {{x_{ij}}} \right\} - {x_{ij}}}}{{\mathop {\max }\limits_i \left\{ {{x_{ij}}} \right\} - \mathop {\min }\limits_i \left\{ {{x_{ij}}} \right\}}},{u_j} \in {T_2}\end{array} \right.$

(14)

这里, ${T_1},{T_2}$ 分别表示指标属于“越大越优型”和“越小越优型”.

3.2 基于灰色关联度的相关性分析

本文利用数据集内10组融合图像, 分别计算两两客观评价指标间的灰色关联度, 并求其均值. 计算结果见表1所示.

图3给出了基于灰色关联度的动态聚类图. 由公式(12)和公式(13)确定聚类阈值 $\theta {\rm{ = }}0.9$ , 由图3可知的聚类结果为:

$\left\{ {\left( {3,10} \right), \left( {1,11} \right), \left( {2,8,4,6} \right), \left( {5,9,7} \right)} \right\}$

3.3 基于斯皮尔曼等级相关系数的分析

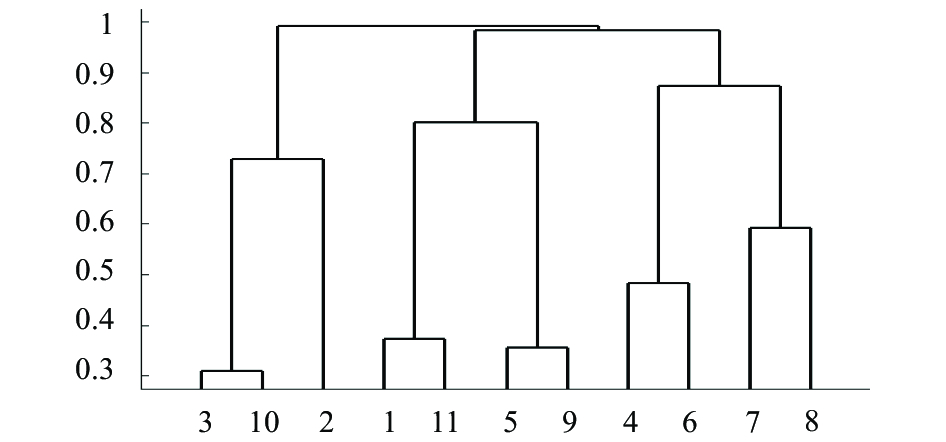
图4给出了基于斯皮尔曼相关系统的动态聚类图.

确定聚类阈值 $\theta {\rm{ = }}0.9$ , 由图4可以看出聚类结果为:

$\left\{ {\left( {3,10,2} \right),\left( {1,11,5,9} \right),\left( {4,6,7,8} \right)} \right\}$

显然, 上述两种聚类结果不一致, 这是因为基于灰色关联度的聚类方法反映两变量间的相关系数; 基于斯皮尔曼等级相关系数的聚类分析法反映两变量之间联系的强弱程度. 结合上述两种分类结果, 将上述11个评价指标分为6类, 即:

$\left\{ {\left( {3,10} \right),\left( {1,11} \right),\left( {5,9} \right),\left( {4,6,8} \right){\rm{,2,7}}} \right\}$

因此, 在建立红外与可见光图像融合质量评价指标体系时, 可以选择相关性较低的评价指标, 保证了评价指标的合理性和非冗余性, 既提高了综合评价的速度, 同时也保证了综合评价的合理性.

4 结论与展望

红外与可见光图像融合质量评价能够进一步丰富和完善图像融合理论框架. 单个评价指标往往不能准确地评价图像融合质量, 需要进行综合评价. 评价指标体系是进行综合评价的关键, 它的建立应该满足非冗余性原则. 本文选取有代表性的评价指标共计11个, 采用斯皮尔曼相关等级系数和灰色关联度研究评价指标的相关程度, 在此基础上分析阈值变化率选取最优聚类阈值, 将评价指标进行分类. 为后续研究红外与可见光图像融合质量综合评价提供理论支持.