2. 广州中国科学院沈阳自动化研究所分所, 广州 511458
2. Shenyang Institute of Automation, Guangzhou, Chinese Academy of Sciences, Guangzhou 511458, China
随着社会和科技的发展, 人们的生活水平不断提高, 对于高营养价值的生鲜货物的需求量增加迅速, 使冷藏运输工具及技术也得以发展[1]. 航运咨询机构德路里(Drewry)预计, 到2020年, 海运冷藏货物贸易量预计将达到1.2亿吨, 平均每年的海运量将以2.5%的速度增长. 由于海运货物量不断增加, 冷藏集装箱使用率将出现提高, 冷藏集装箱船在市场上的份额也将不断上升. 数据表明[2], 冷藏集装箱及风机的实际消耗功率约占船舶总负载2/3左右, 且冷藏集装箱总制冷功率需求波动大, 这直接影响了船舶电站容量的配置. 减小冷藏集装箱总制冷功率需求的波动, 可降低船舶电站装机容量或增大冷藏集装箱的装载量, 无论是对于航运公司降低运营成本还是对各制冷机组制造商抢占市场都具有重要的意义.
1 现状分析目前, 集装箱船对各冷藏集装箱的控制相互独立, 船上缺乏对冷藏集装箱的统一管理, 且单个冷藏集装箱工况是全自动的, 也就是对电力需求是随机的, 可能造成总制冷功率需求出现较大的波动. 为应付最劣情况, 船上制冷发电机组必须根据冷藏集装箱制冷的最大功率工况进行配置以保证船上的电力安全, 由此可能出现的频繁峰谷变化会导致船上的发电机组难以长时间以合适的负荷率运行, 造成船舶营运成本增加和实际使用功率闲置[3].
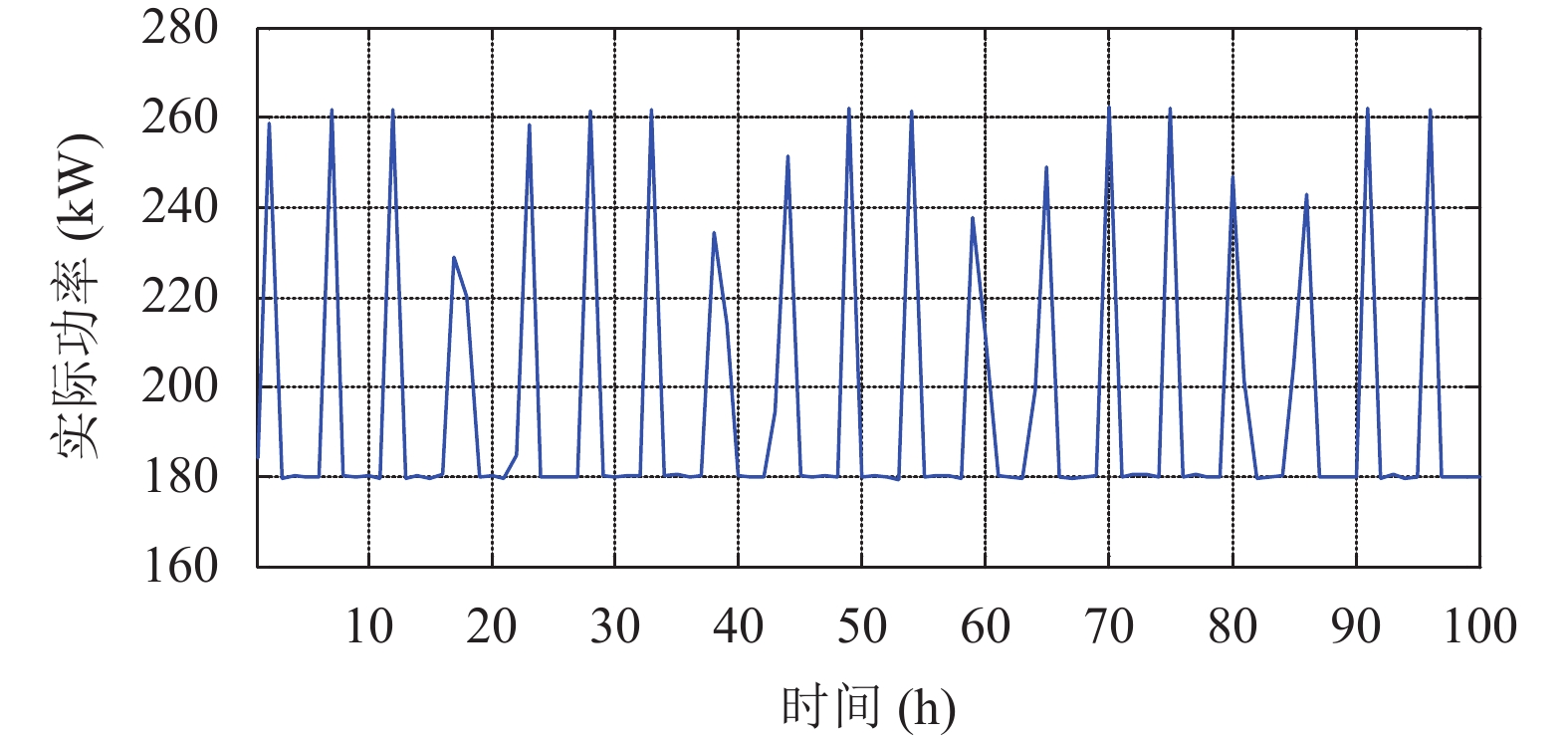
冷藏集装箱船100 h时间内50箱冷藏集装箱自然情况下的电力需求变化情况如图1.
从图1可看出, 冷藏集装箱只在部分时间内以最大功耗工作, 其他时间的功率需求较为稳定. 冷藏集装箱的总电力需求存在较大的波动, 存在多个波峰波谷, 峰谷变化频繁且峰谷差值较大.
因此, 有必要对冷藏集装箱进行功率平衡, 实现优化调度管理, 起到平抑电力峰值需求, 降低船舶电站装机容量或增大冷藏集装箱装载量的作用.
|
图 1 自然状态下实际功率变化曲线 |
国内外众多学者对优化调度问题的建模及求解展开大量的研究工作. 文献[4]建立集装箱场桥的智能调度优化数学模型, 设计基于遗传算法的求解策略, 验证该方法可较大幅度地缩短作业时间, 降低运作成本. 文献[5]提出一种平板车运输调度遗传算法模型, 表明该模型可获得较优的平板车调度任务计划, 提高平板车的运输效率. 采用遗传算法求解优化调度问题, 具有极高鲁棒性及广泛适用性, 但其存在收敛速度慢, 容易陷入局部最优的不足, 将量子计算与遗传算法的原理相结合, 可克服遗传算法的这些缺点. 例如, 文献[6]建立水电站群长期优化调度模型, 并提出了一种具有量子行为的遗传算法对其求解; 文献[7]利用量子遗传算法, 在流水车间调度及随机作业车间调度方面取得了良好的效果.
本文对冷藏集装箱优化调度问题建立数学模型, 确定其优化目标及约束条件, 对该问题采用一种基于量子遗传算法的方法求解, 以获得冷藏集装箱的最优调度策略.
2 冷藏集装箱优化调度问题数学模型不同类型货品的制冷保鲜原理有所不同, 冷冻类货品, 冷藏类货品及温控类货品的控温范围如表1所示[3].
| 表 1 几类货品的温控范围(℃) |
冷藏集装箱需根据其装载货品的不同种类采取不同的控温制冷方式, 以保证货品质量.
2.1 温度等级划分假设船上设有n个冷藏集装箱, 各个冷藏集装箱的温度为Ti(i=1, 2, …, n), 初始温度Ti都处在保证货品质量的温度范围内, 在该算法模型中应划分冷藏集装箱的温度等级, 对冷藏集装箱的温度进行制冷排队, 假设第i个冷藏集装箱在时刻t下的温度值为Ti, 其装载货品温度范围的上下界为Tl, Tu,
| ${\text{划分温度等级}}\left\{ {\begin{aligned}& {{\text{维持}},\;\;\;\;\;\;{T_i} < {T_u} - \Delta {T_{{\text{控}}}}}\\& {{\text{优先}},\;\;{T_l} < {T_i} < {T_l} + \Delta {T_{{\text{控}}}}}\\& {{\text{立即}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{T_i} > {T_l}}\end{aligned}} \right.$ | (1) |
由文献[3]可知, 冷藏集装箱箱内温度的变化过程可以视作一个线性变化模型. 在外界温度不变的情况下, 经过时间Δt小时之后, 对于某个冷藏集装箱在不制冷的情况下, 可求得它在Δt时间后箱内温度的变化量
| $\Delta T = b * ({T_1} - {T_2}) * \Delta t$ | (2) |
其中, T1为箱外温度, T2为箱内温度, b为冷藏集装箱不制冷状态时箱内温升系数;
冷藏集装箱在制冷的情况下, 经过Δt时间后, 其箱内温度变化量
| $\Delta T = k * ({T_1} - {T_2}) * \Delta t$ | (3) |
其中, k为制冷时箱内温降系数.
由于受到周围环境的干扰, 冷藏集装箱的温度总是处于不断变化之中. 因此, 为冷藏集装箱的温度加上一个扰动
根据冷藏集装箱的温度来判定其状态, 执行冷藏集装箱的制冷和不制冷状态的切换, 将冷藏集装箱i的工作状态模型表示如下:
| ${S_{{i}}} = \left\{ {\begin{array}{*{20}{l}}{0,\;\;{\text{不制冷}}}\\{1,\;\;{\text{制冷}}}\end{array}} \right.,\;\;\;i = 1,2, \cdots, n$ | (4) |
Si为一个二值函数, 用于表示冷藏集装箱的状态.
2.4 冷藏集装箱温度, 状态, 功率之间的关系冷藏集装箱温度等级与其状态的关系表示如下:
| ${S_i} = \left\{ \begin{array}{l}0,\;\;{\text{维持}}\\0 {\text{或}}1 ,\;\;{\text{优先}}\\{\rm{1,}}\;\;{\text{立即}}\end{array} \right.$ | (5) |
由文献[8]可知, 冷藏集装箱的实际输入功率取决于其运行状态和内外温差. 表2的数据为外界温度为37.8 ℃和电网频率为60 Hz时的两种冷藏集装箱在不同箱内温度情况下对应的制冷量和输入电功率. 在本模型中, 对404A涡旋式压缩机的冷藏集装箱进行讨论[8,9].
| 表 2 冷王制冷机组的制冷量和电功率数据 |
对冷藏集装箱[–29 ℃, –18 ℃]及(–18 ℃, 2 ℃]两个温度范围下的输入电功率的变化曲线分段拟合成一次函数曲线. 对于冷藏集装箱的输入电功率有, 当冷藏集装箱不制冷时, 即S=0时:
| ${P_i} = a$ | (6) |
当冷藏集装箱制冷时, 即S=1时:
| ${P_i} = \left\{ {\begin{array}{*{20}{l}} { - 0.15({T_c} - {T_i}) + 14.47, \;\;- 18 < {T_i} \leqslant 2} \\ { - 0.07273({T_c} - {T_i}) + 10.16,\;\; - 29 \leqslant {T_i} \leqslant - 18} \end{array}} \right.$ | (7) |
其中, a, Tc均为常数, Tc为环境温度.
冷藏集装箱的电力需求会受到季节, 纬度, 环境温度, 及装箱位置的影响, 对于冷藏集装箱功率, 根据经验值, 添加一个扰动
| ${P_i} = {P_i} + {\varepsilon _2}$ | (8) |
冷藏集装箱船上会开启风机为工作中的冷藏集装箱散热, 以满足冷藏集装箱的制冷需求[8]. 在本文中, 根据集装箱船货舱风机配置方案, 设置一台货舱风机负责给一组10个冷藏集装箱提供风量. 本文将风机的数量设为l, 风机的功率设为p(常数), 冷藏集装箱的运行状态与风机运行状态Sf存在这样的关系; 即有冷藏集装箱处于制冷状态时, 风机就必须启动. 对于一组冷藏集装箱, 将二者的关系表示如式(9).
| ${S_f} = \left\{ {\begin{array}{*{20}{c}} {p,\sum\limits_{j = 1}^{10} {{S_j} \ne 0} } \\ {0,\sum\limits_{j = 1}^{10} {{S_j} = 0} } \end{array}} \right.$ | (9) |
对于冷藏集装箱功率平衡调度问题, 已知冷藏集装箱的稳定状态下的功率约等于总制冷功耗的均值Pavr, Pavr为冷藏集装箱最大总制冷功耗Pzmax的1/3, 在满足各项约束条件的前提下, 以求平均制冷功耗与总事实功率差值的绝对值的最小值为优化目标, 找出最接近平均制冷功耗的总事实功率[9,10]. 冷藏集装箱总事实功率由两部分功率组成, 一是各冷藏集装箱功率之和, 二是各风机功率之和. 在某时刻t时, 目标函数可表示如下:
| $Minimize:\;\;\Delta P = \left| {{P_{\rm{avr}}} - \sum\limits_{i = 1}^n {{P_i} - \sum\limits_{j = 1}^l {{P_f}} } } \right|$ | (10) |
| $Subject:\;\;{T_l} < {T_i} < {T_u},\;\;i = 1,2,3, \cdots, n$ | (11) |
式中, Pavr表示总制冷功耗的平均值, n为冷藏集装箱的个数, Pi(i=1, 2, …, n)是各冷藏集装箱的功率, l表示风机个数, Pf为风机功率.
冷藏集装箱功率平衡调度问题旨在搜索一个与平均总制冷功耗相差最小的总事实功率值, 是一种目标寻优问题. 群智能优化算法如遗传算法适合用于解决该类问题. 遗传算法(GA)模拟生物进化过程的优胜劣汰规则与染色体交换机制, 通过选择, 交叉, 变异三种基本操作寻找最优个体. 但是遗传算法的收敛速度慢, 且容易陷入局部最优[11,12]. 量子遗传算法(QGA)结合了量子计算与遗传算法的原理, 使用量子比特的几率幅来表示染色体的编码, 并利用量子旋转门实现染色体的更新操作, 完成进化搜索, 可以克服常规遗传算法易发生未成熟收敛, 且收敛速度慢的缺点, 达到更好的搜索效果[13].
3 算法寻优过程 3.1 量子遗传算法寻优过程(1) 量子比特编码
采用量子比特编码染色体的各个基因, 假设染色体有n个基因, m表示进化代数, 则第m代, 第j个染色体
| $Q_j^m = \left( {\begin{array}{*{20}{c}} {\alpha _1^m} \\ {\beta _1^m} \end{array}\left| {\begin{array}{*{20}{c}} {\alpha _2^m} \\ {\beta _2^m} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {\alpha _3^m} \\ {\beta _3^m} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {...} \\ {...} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {\alpha _{n - 1}^m} \\ {\beta _{n - 1}^m} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {\alpha _n^m} \\ {\beta _n^m} \end{array}} \right.} \right)$ | (12) |
其中,
(2) 初始化种群
随机生成M个以量子比特为编码的染色体, 将种群中全部染色体的所有基因
(3) 测量个体
对初始种群中的各个个体测量, 获得一组确定的解, 该解是长度为n的二进制序列. 在本文中冷藏集装箱的工作状态是用0-1二值函数来表示的, 0表示不制冷, 1表示制冷, 即, 这一组二进制序列可视作一组冷藏集装箱的工作状态序列. 每个基因位上是0或1根据量子比特的概率(
(4) 计算适应度
该问题的优化目标是求解平均制冷功耗与总事实功率差值的绝对值的最小值. 因此, 在该步骤设适应度函数为目标函数的相反数, 即, 目标函数值越小的个体, 其适应度值越大. 适应度函数Fi, 表示如下:
| ${F_i} = - \Delta P = - \left\{ {\left| {{P_{avr}} - \sum\limits_{i = 1}^n {{P_i}} - \sum\limits_{j = 1}^l {{P_f}} } \right|} \right\}$ | (13) |
计算出各个个体的适应度之后, 记录下最优个体和其对应的适应度, 同时将其作为下一步进化的目标值.
(5) 量子旋转门更新
量子旋转门的调整操作为(14):
| $U({\theta _i}) = \left[ {\begin{array}{*{20}{c}} {\cos ({\theta _i})}&{ - \sin ({\theta _i})} \\ {\sin ({\theta _i})}&{\cos ({\theta _i})} \end{array}} \right]$ | (14) |
更新过程表示成(15):
| $\left[ {\begin{array}{*{20}{c}} {\alpha _i'} \\ {\beta _i'} \end{array}} \right] = U({\theta _i})\left[ {\begin{array}{*{20}{c}} {{\alpha _i}} \\ {{\beta _i}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos ({\theta _i})}&{ - \sin ({\theta _i})} \\ {\sin ({\theta _i})}&{\cos ({\theta _i})} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\alpha _i}} \\ {{\beta _i}} \end{array}} \right]$ | (15) |
其中,
算法进入迭代过程后, 以记录下的最优个体作为进化方向, 根据设定的调整策略, 利用量子旋转门更新种群, 再记录下当前种群中的最优个体并与之前的目标值比较, 从而决定下次迭代的目标值, 如此往复, 直到迭代次数终止.
3.2 参数选择(1) 量子遗传算法各项参数
种群大小M及每个个体的二进制长度(冷藏集装箱数量)n由问题规模大小确定, 设计问题规模M×n分别为20×30, 40×50, 70×80的三个算例, 进化终止代数MAXGEN为200. 量子旋转门旋转角调整方案如表3.
同时, 为验证QGA对冷藏集装箱功率平衡优化调度的效果, 设计相同条件(种群大小, 个体长度, 进化代数)下, GA对冷藏集装箱优化调度的实验进行对比. 采用二进制编码, 轮盘赌选择, 单点交叉, 交叉概率为Px=0.7, 二进制变异, 变异概率Pm=0.01.
| 表 3 旋转角调整方案 |
(2) 算例的各项参数
以下表中的各项参数为算例进行仿真. 算例中的参数如表4所示.
| 表 4 冷藏集装箱各项参数及取值 |
3.3 结果
本文分别用GA和QGA对问题规模M×n分别为

|
图 2 M=20, n=30的实际功率变化情况 |
|
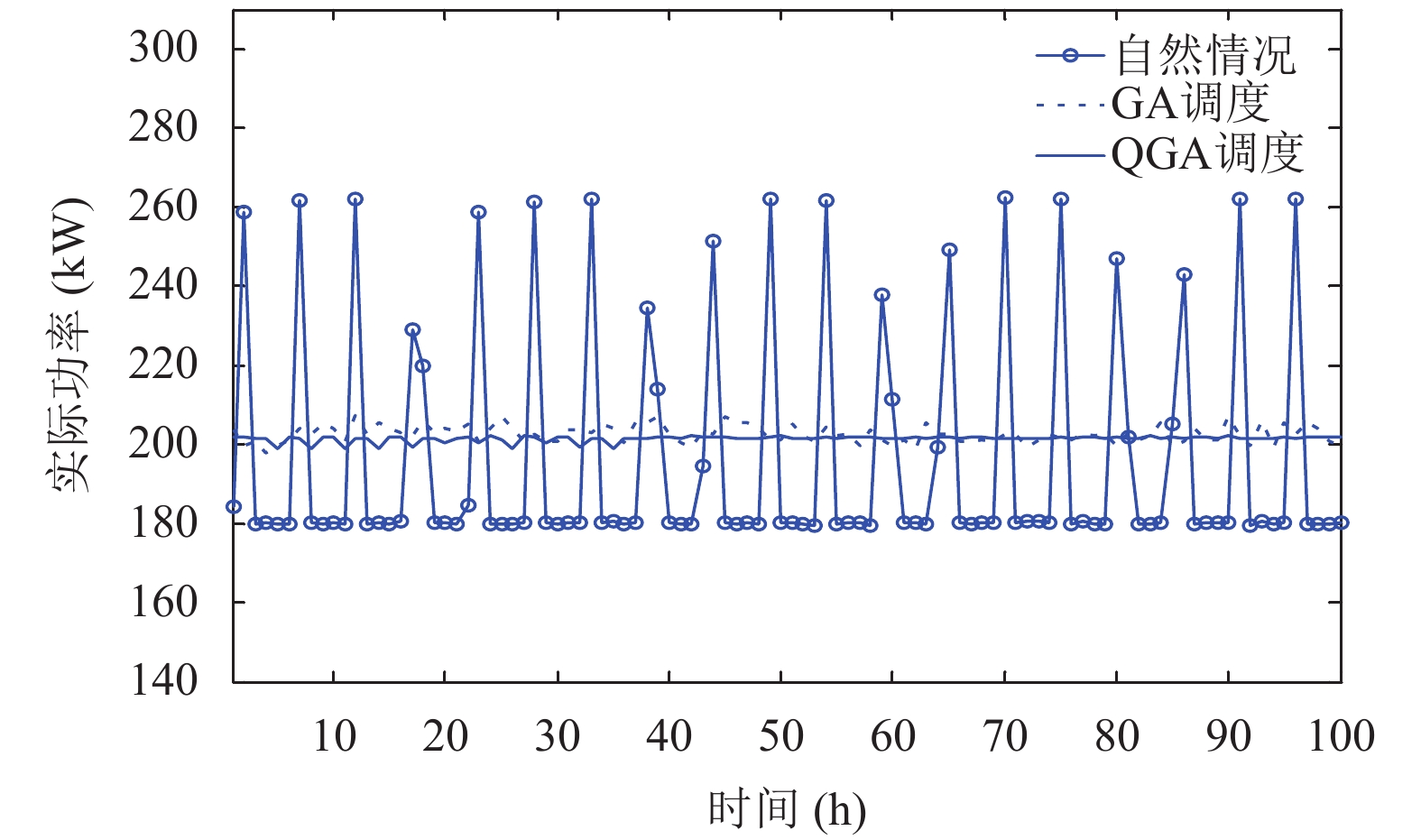
图 3 M=40, n=50的实际功率变化情况 |
|
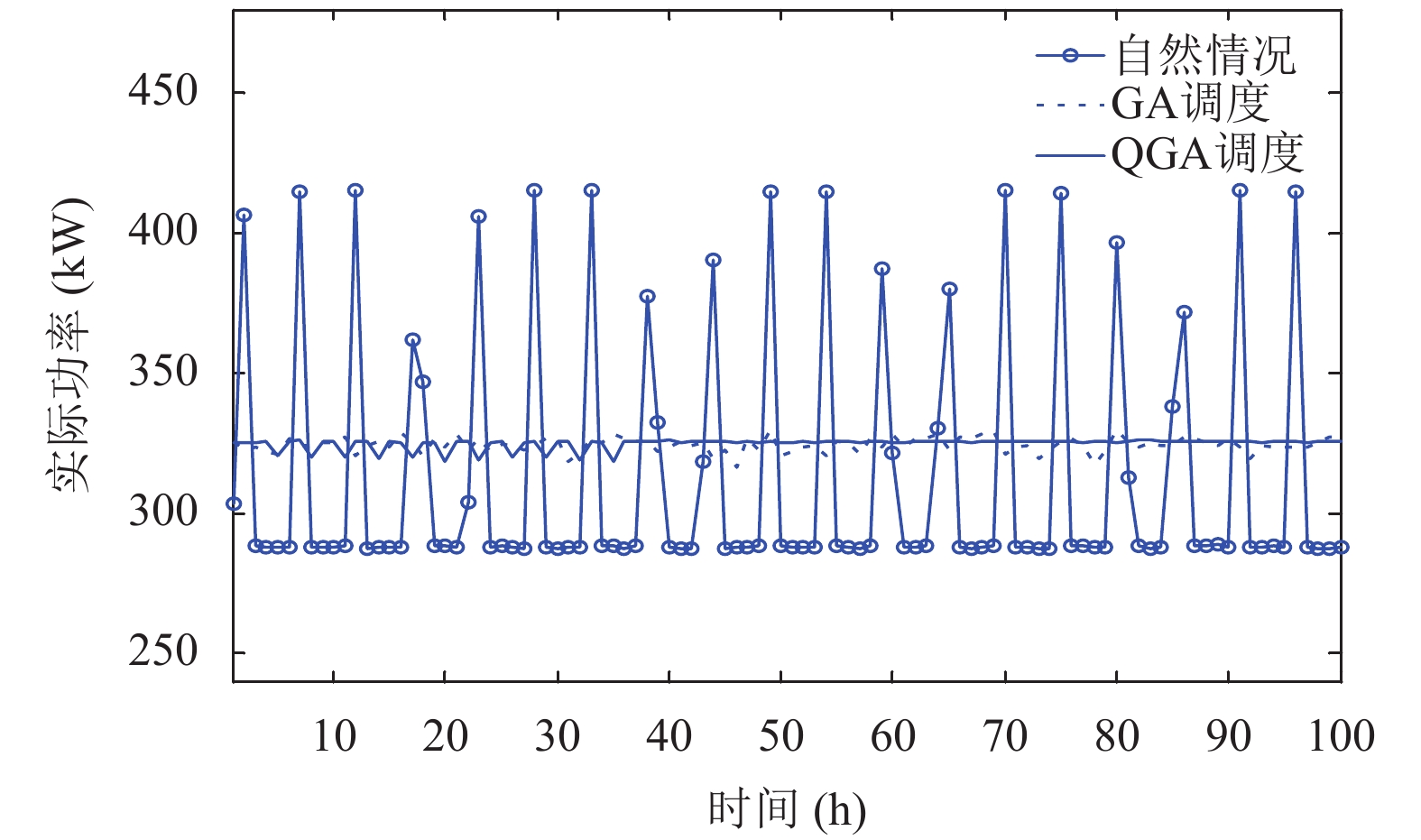
图 4 M=70, n=80的实际功率变化情况 |
4 分析与比较 4.1 算法收敛度
GA中采用二进制编码, 每个基因位只能表示0或1的状态, 而在QGA中, 一个量子位不仅仅只能表示0或1的状态, 还能表示两种状态间的任意叠加态. QGA采用的这种量子比特染色体的表示形式, 使一个染色体可以同时表示多个状态信息, 这样就可以大大减少染色体数目, 并且可以在较小的种群规模的情况下, 仍然能保持种群的多样性, 相比GA来说, QGA能克服早熟收敛, 个体具有跳出局部极值的能力.
|
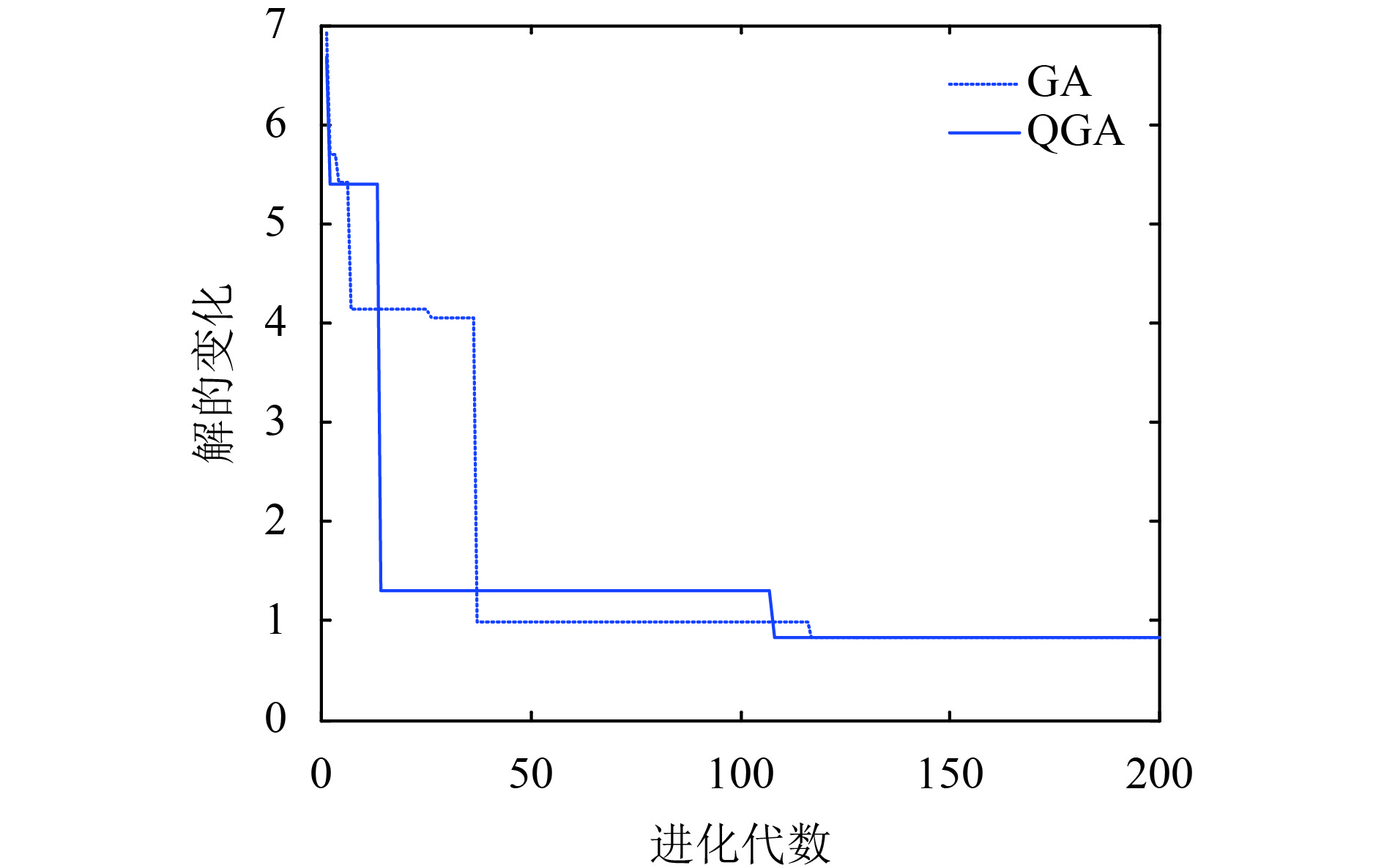
图 5 M=20, n=30算法收敛图 |
|
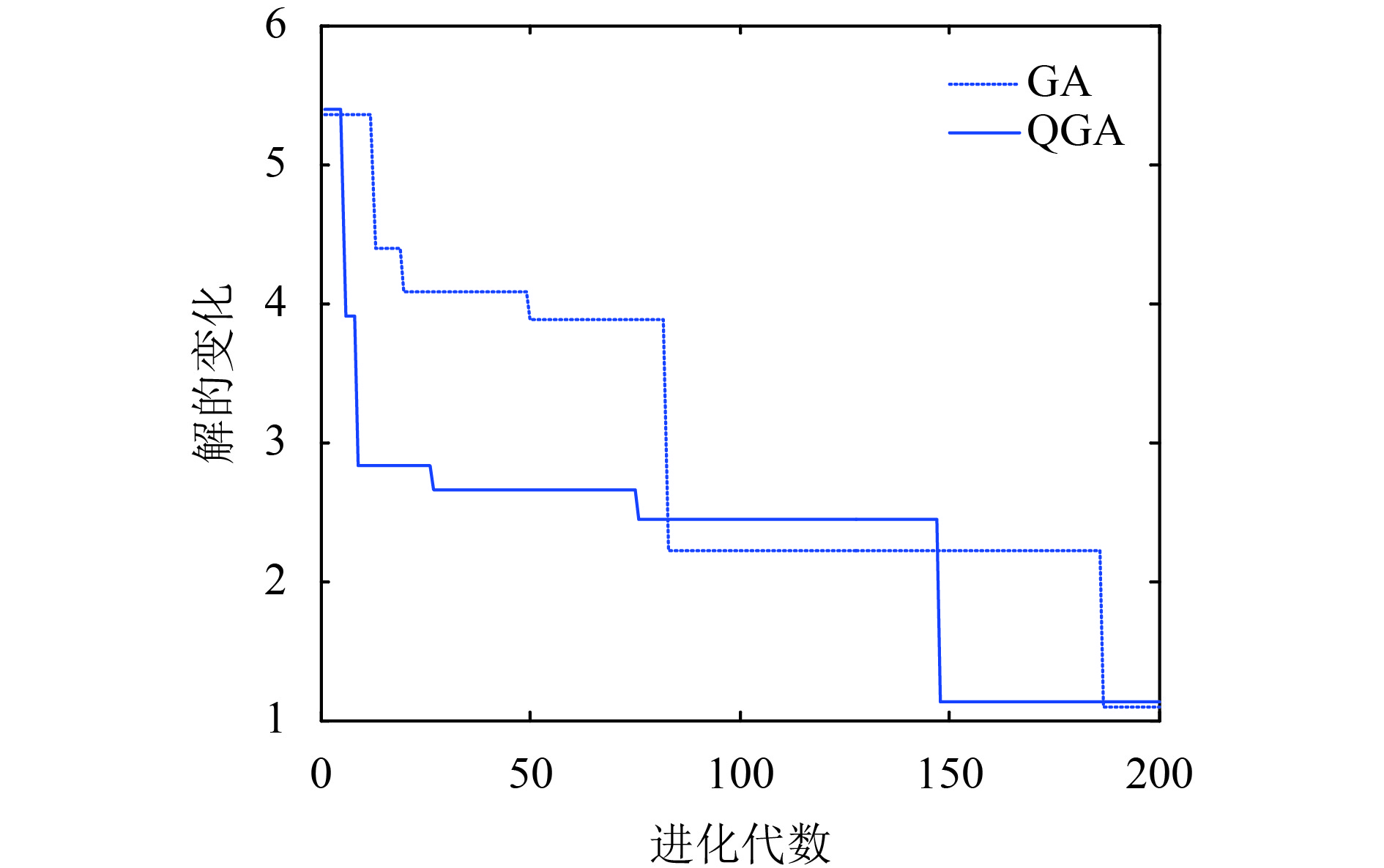
图 6 M=40, n=50算法收敛图 |
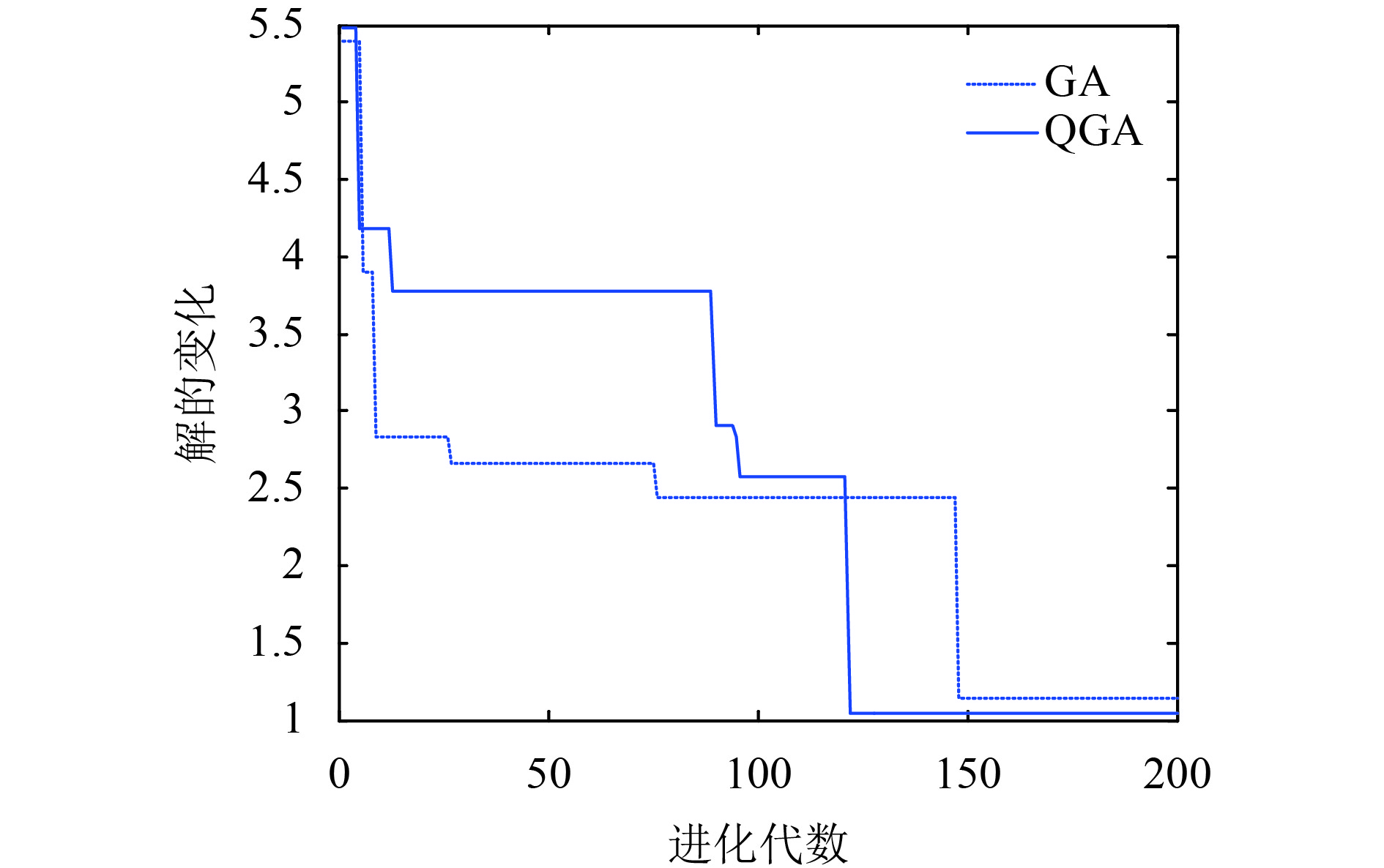
由图5, 6, 7及表5数据可知, 在不同问题规模下, QGA的收敛速度都要优于GA的收敛速度, 都能获得较好的最优解. 在种群规模为20×30时, 由于问题规模还较小, GA和QGA的整体趋势是一致的, 没有出现明显的差异, 且最终搜索到的最优解相同, 且最终收敛代数接近. 而当问题规模增大为40×50及70×80时, 两类算法的寻优效率发生变化, 从算法迭代的中后期可以看出, QGA相比GA具有较快的收敛性, 能够更早地使整个群体趋向最优解. 由此可得, QGA相比GA求解冷藏集装箱最优调度策略的能力更优.
|
图 7 M=70, n=80算法收敛图 |
| 表 5 不同问题规模的算法收敛过程 |
4.2 均值及标准差
从图2, 3, 4可看出, GA及QGA对改善总制冷功率的数据波动情况都有着显著作用. 由表6中数据可知, 随着装箱数量的增加, 自然情况, GA和QGA调度下的冷藏集装箱的实际功率的均值及标准差也在上升, 这说明冷藏集装箱数量的增加会使得其所需的总平均制冷功率增加, 总电力需求不稳定. 将各情况下的均值和标准差数据比较可知, 经GA和QGA调度后冷藏集装箱总制冷功率的均值十分接近, 且都接近算例中设定的目标值Pavr, 它们的标准差值都远小于自然情况下的标准差值. 但在三个算例下经QGA调度后的冷藏集装箱总制冷功率的标准差小于经GA调度后的标准差的72%, 说明QGA在平衡冷藏集装箱总制冷功率, 减小冷藏集装箱总制冷功率需求波动方面的能力更强.
4.3 峰谷差从图2, 3, 4可看出, 自然情况下的冷藏集装箱总制冷功率存在频繁的峰谷变化, 且峰谷差大, 经GA及QGA调度后冷藏集装箱实际功率变化的波动范围大大缩小. 由表6中数据可知, 随着装箱数量的增加, 冷藏集装箱的总实际功率的峰值, 谷值, 峰谷值差值都随之增大. 由数据计算可得, 经GA调度后的冷藏集装箱总制冷功耗的峰谷值差值小于自然状态下的峰谷值差值的15%, 经QGA调度后的冷藏集装箱总制冷功耗的峰谷值差值小于自然状态下的峰谷值差值的6%, 且小于经GA调度后的峰谷值差值的60%. 由此可知, QGA和GA都能很大程度上减小冷藏集装箱总制冷功耗的峰谷差, 但是, QGA相比GA能更好地对冷藏集装箱总实际制冷功耗起到“削峰填谷”的作用.
| 表 6 三种情况下的各项指标比较 |
4.4 船舶电站设计容量
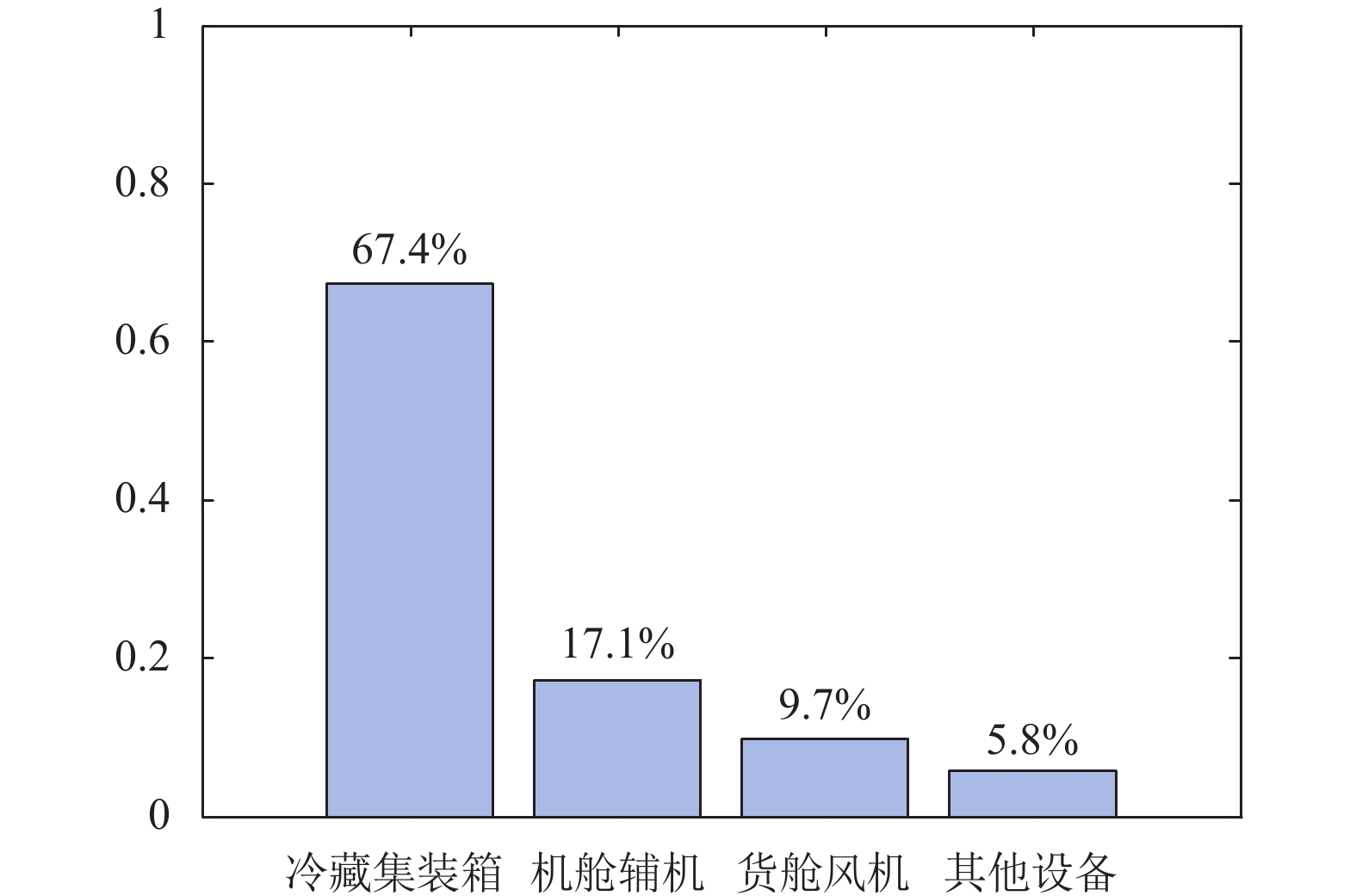
以文冲船厂制造的某集装箱船的电力负荷计算书为例, 可计算出各用电设备在海上航行工况的实际消耗功率. 各部分消耗功率占比分配如图8所示.
|
图 8 冷藏集装箱船上各用电设备的实际消耗功率 |
船舶电站容量通常由三类负荷法和需要系数法这两种方法获得. 其中比较常用的方法是需要系数法. 需要系数法定义为用电设备实际消耗功率与其额定所需总功率的比值[2]. 参考该集装箱船电站设计中的冷藏集装箱使用系数的设计方法, 通过需要系数法可以求得冷藏集装箱峰值所对应的额定设计容量.
由图8可知, 冷藏集装箱及货舱风机占总负载的比重x为77.1%. 以此百分比对算例的船舶电站容量计算, 可求出自然情况下及经两类调度算法后的船舶电站设计容量, 即表6中“设计容量”一栏. 由表中数据计算可知, 经GA调度后对船舶电站容量的配置减小了21%左右, 经QGA调度后对船舶电站容量的配置减小了23%左右, 两类调度算法均可减小船舶电站的装机容量, 降低船舶电站配置裕度, 但经QGA调度后节约的电站容量略高于GA, 其优化电站配置能力更强. 这也就意味着, 在同样的电站容量下, QGA能装载较多的冷藏集装箱.
5 结语本文对冷藏集装箱功率平衡调度问题进行理论分析, 提出了一种基于量子遗传算法(QGA)的集装箱船功率平衡调度方法, 并设计算例在MATLAB平台下进行仿真实验, 同时, 将经QGA调度与经GA调度后的冷藏集装箱总制冷功率的变化情况及各项指标值进行分析比较, 得出如下结论:
(1) QGA与GA均对冷藏集装箱的总制冷功率需求起到“削峰填谷”的作用, 但是, QGA在求解最优调度策略时的收敛速度更快. 经QGA调度后的实际功率曲线的波动更小, 总制冷功率峰谷值差值更小, 数据趋于平稳.
(2) 使用QGA与GA对冷藏集装箱进行功率平衡优化调度都能降低船舶电站配置容量, 或在同等设计容量下, GA和GA都可增加船舶的装箱数量, 提高船舶经济效益. 但经QGA调度后, 节约的电站容量略高于GA, 经济效益更显著.
| [1] |
杨明亮. 船用冷藏集装箱制冷机组及其控制装置的研发[硕士学位论文]. 厦门: 集美大学, 2016.
|
| [2] |
单海校, 张华. 船舶电站及其自动化. 北京: 海洋出版社, 2016.
|
| [3] |
陆毅华, 周晓莹. 冷藏集装箱功率平衡系统研究. 广东造船, 2017, 36(1): 52-55. DOI:10.3969/j.issn.2095-6622.2017.01.023 |
| [4] |
初良勇, 阮志毅, 李淑娟. 基于遗传算法的港口集装箱堆场场桥智能调度优化. 中国航海, 2018, 41(1): 48-52. DOI:10.3969/j.issn.1000-4653.2018.01.010 |
| [5] |
孟令通, 朱洪渊, 蒋祖华, 等. 基于遗传算法的平板车调度优化方法. 哈尔滨工程大学学报, 2018, 39(3): 554-560. |
| [6] |
Sun J, Fang W, Wang DJ, et al. Solving the economic dis-patch problem with a modified quantum-behaved particle swarm optimization method. Energy Conversion and Management, 2009, 50(12): 2967-2975. DOI:10.1016/j.enconman.2009.07.015 |
| [7] |
Gu JW, Gu MZ, Cao CW, et al. A novel competitive co-evolutionary quantum genetic algorithm for stochastic job shop scheduling problem. Computers & Operations Research, 2010, 37(5): 927-937. |
| [8] |
Meier-Peter H, Bernhardt F. 船舶工程技术手册. 王平庚, 译. 上海: 上海交通大学出版社, 2009.
|
| [9] |
陈立华, 梅亚东, 董雅洁, 等. 改进遗传算法及其在水库群优化调度中的应用. 水利学报, 2008, 39(5): 550-556. DOI:10.3321/j.issn:0559-9350.2008.05.006 |
| [10] |
Ghoseiri K, Szidarovszky F, Asgharpour MJ. A multi-objective train scheduling model and solution. Transportation Research Part B: Methodological, 2004, 38(10): 927-952. DOI:10.1016/j.trb.2004.02.004 |
| [11] |
Bazzazi M, Safaei N, Javadian N. A genetic algorithm to solve the storage space allocation problem in a container terminal. Computers & Industrial Engineering, 2009, 56(1): 44-52. |
| [12] |
钟求喜, 谢涛, 陈火旺. 基于遗传算法的任务分配与调度. 计算机研究与发展, 2000, 37(10): 1197-1203. |
| [13] |
Peng WM, Deng HF. Quantum inspired method of feature fusion based on von Neumann entropy. Information Fusion, 2014, 18: 9-19. DOI:10.1016/j.inffus.2013.10.003 |
| [14] |
He Y, Deng Y, Luo MX. The improved evolution paths to speedup quantum evolution. International Journal of Theoretical Physics, 2016, 55(4): 1977-1987. DOI:10.1007/s10773-015-2838-1 |
 2018, Vol. 27
2018, Vol. 27


