在机器人轨迹规划的过程中会产生震荡, 造成额外能量消耗. 而在定点运动中, 不同的运动轨迹会造成不同程度的抖振. 如何设计机器人的最优轨迹优化问题受到了工业界和学术界的广泛关注. 传统的机器人轨迹规划多以运行时间指标为目标, 采用B 样条插值对一系列离散路径点拟合[1], 在边界层出现稳态跟踪误差, 运动平稳性较差. 近几年, 杨国军等[2]对简单遗传算法进行了改进, 将模糊原理应用于遗传算法, 提出了一种基于模糊遗传算法的机械手时间最优轨迹规划方案. 王宪等[3]提出基于改进蚁群算法的机器人轨迹规划, 引入带方向信息的全局启发因子来提高最优路径的搜索效率. 甘亚辉等[4]采用遗传算法综合考虑各机器人沿轨迹运动的安全性, 运动代价以及运动约束, 获得了单个机器人规划最优的运动轨迹. 付荣等提出了关节空间基于粒子群优化[5]和自适应遗传算法[6]的时间最优3-5-3多项式插值轨迹规划算法, 解决了由于多项式插值轨迹规划具有阶次高, 没有凸包性质的缺点, 难以应用传统优化方法进行优化的问题. 王学琨等[7]针对六自由度关节型解耦机械臂在抓取目标物体过程中出现的不稳定性、快速性以及最大速度约束的问题, 提出了一种利用DE算法优化的时间最优3-5-3多项式插值机械臂轨迹规划算法. 余阳[8], 赫建立等[9]采用高次均匀B样条插值, 提出了基于遗传算法的轨迹规划方案, 该方案比较理想化地兼顾了工业机器人工作效率与轨迹的平稳性. 刘一扬等[10]改进了遗传算法的机器人运动轨迹跟踪控制, 在机器人运动轨迹滑模面设计一个跟踪误差的积分补偿器, 缓解了运动轨迹跟踪控制在边界层出现稳态跟踪误差. 邓飙等[11]使用五次B样条插值规划轨迹, 引入了罚函数处理约束条件, 利用非支配排序遗传算法(NSGA-II) 对轨迹进行多目标优化, 选择了最为平滑且时间最优的解作为最终解. 殷凤健等[12]利用三次样条插值和自适应遗传算法对运动轨迹进行了时间最短优化, 并利用罚函数解决了系统运动的约束问题. 对于固定时间顶点的最优轨迹规划问题的目标函数, 求得了使得整个运动过程消耗最小的能量函数. 梁延德等[13]在每两个相邻的目标点之间构造分段数为7的三次样条函数, 证明了此时的插值函数有能力描述时间最短的轨迹问题, 并用BFGS 方法进行了优化计算.
对于机器人可行轨迹的规划问题, 上述算法往往仅在以总时间为指标的目标函数上加上其他项, 或者增大拟合多项式的次数, 增大样条函数的次数上进行了改进. 但是人工参与设置的参数过多, 模型不稳定以及拟合过冲导致运动轨迹震荡的情况还未引起学者的足够重视.
本文针对种群优化算法中人工参数设置过多, 模型训练过程不稳定以及拟合过冲导致运动轨迹震荡的情况, 提出了一种基于滑模控制的改进差分进化(IDE)算法. 该算法在变异阶段之前增加筛选阶段, 求出了当前群体的目标函数值最优(适应度值最小)的个体、适应度值最大的个体和所有个体的平均水平. 在变异阶段, 取消了变异因子, 采用适应度值最小的个体和平均水平的个体提高种群中每一个个体的水平, 用适应度值最小的个体替换适应度值最大的个体, 加快收敛速度. 取消了交叉阶段, 减少了交叉因子的两个参数. 在插值方面, 采用了保形分段三次Hermite插值, 降低了插值函数光滑性的要求, 避免了模型不稳定以及拟合过冲导致运动轨迹震荡的情况. 通过仿真实验和结果分析表明, 本文给出的改进差分进化算法与传统方法相比, 该方法具有明显的优势.
1 差分进化算法 1.1 差分进化算法的内容差分进化算法是基于群体智能理论的优化算法, 通过群体中个体间的合作与竞争更新群体, 最终通过迭代更新, 逼近最优解, 因此可用于智能化优化搜索. 标准差分进化算法是根据父代个体间的差分矢量进行变异, 交叉和贪婪选择更新个体. 其基本思想是从某一随机产生的初始群体开始, 通过把种群中任意两个个体的向量差加权后乘上变异因子与第三个个体求和来产生新个体, 然后将新个体与当代种群中某个预先决定的个体相比较, 如果新个体的适应度值优于与之相比较的个体的适应度值, 则在下一代中就用新个体取代旧个体, 否则旧个体仍保存下来, 通过不断地迭代运算, 保留优良个体, 淘汰劣质个体, 引导搜索过程向最优解逼近.
在优化设计中, 差分进化算法与传统的优化方法相比, 具有以下主要特点:
(1) 差分进化算法从一个群体(即多个点)而不是从一个点开始搜索, 这是它能以较大的概率找到整体最优解的主要原因.
(2) 差分进化算法的进化准则是基于适应性信息的, 无须借助其他辅助性信息(如要求函数可导或连续), 大大地扩展了其应用范围.
(3) 差分进化算法具有内在的并行性, 这使得它非常适用于大规模并行分布计算, 减小时间成本开销.
(4) 差分进化算法采用概率转移规则, 不需要确定性的规则.
但是标准的差分进化算法也存在以下问题:
(1)变异阶段随机选取3个个体进行差分, 然后加权求和求出新个体, 进行贪婪选择后, 二选一保留原始个体或者用新个体替代原始个体. 利用随机选取的个体进行更新, 没有充分利用种群中表现最好的个体和种群总体的信息, 收敛的速度和稳定性有待提高.
(2) 为了增大种群多样性, 采用变异因子和交叉因子或者随迭代代数变化的自适应变异因子和交叉因子, 在增大种群多样性, 避免陷入局部最优的同时引入了需要人工干预的两个参数的取值范围. 人工干预参数的引入, 使得调参对于结果的影响很大, 这不利于算法的应用和推广.
1.2 改进差分进化算法的内容基本流程标准差分进化算法是基于实数编码的进化算法, 整体结构上与其他进化算法类似, 由变异, 交叉和选择三个基本操作构成. 改进的差分进化算法取消了交叉操作, 主要包括以下几个步骤:
(1) 生成初始群体
在
| ${x_{ij}}(0)=r(x_{ij}^{{U}}- x_{ij}^{{L}})+x_{ij}^L$ | (1) |
其中,
(2) 筛选操作
计算所有个体的适应度值, 对所有个体按照适应度值进行排序, 求出最大、最小适应度值的个体和所有个体的平均值
| ${x_{\rm{best}}}(t)=\{ {x_{ij}}|\min (f({x_{i1}},{x_{i2}}, \cdots,{x_{in}}))\} $ | (2) |
| ${x_{\rm{bad}}}(t)=\{ {x_{ij}}|\max (f({x_{i1}},{x_{i2}}, \cdots,{x_{in}}))\} $ | (3) |
其中,
| ${x_{\rm{mean}}}(t)=mean({x_1},{x_2}, \cdots,{x_n})$ | (4) |
其中,
(3) 变异操作
对所有个体进行的变异操作为:
| ${x_{ij}}(t + 1) = {x_{ij}}(t) + rand(({x_{\rm{best}}}(t) - {x_{\rm{mean}}}(t))$ | (5) |
对表现最差个体的操作为:
| ${x_{\rm{bad}}}(t + 1) = {x_{\rm{best}}}(t)$ | (6) |
其中,
(4) 选择操作
为确定
| ${x_{ij}}(t + 1) = \left\{ {\begin{array}{*{20}{c}}{\displaystyle\frac{1}{2}({x_{ij}}^L + {x_{{\rm{best}},j}}),{x_{ij}}(t) < {x_{ij}}^L}\\{\displaystyle\frac{1}{2}({x_{ij}}^U + {x_{{\rm{best}},j}}),{x_{ij}}(t) > {x_{ij}}^U}\end{array}} \right.$ | (7) |
| ${F_{\rm{next}}}=f({x_{i1}}(t+1), \cdots,{x_{in}}(t+1))$ |
| ${F_{\rm{now}}}=f({x_{i1}}(t), \cdots,{x_{in}}(t))$ |
| ${x_j}(t+1)=\left\{ {\begin{array}{*{20}{c}} {{x_j}(t+1),{F_{\rm{next}}} < {F_{\rm{now}}}} \\ {{x_j}(t),{F_{\rm{next}}} < {F_{\rm{now}}}} \;\;\quad\quad\end{array}} \right.$ | (8) |
其中,
对于标准差分进化算法而言, 为了取得理想的结果, 需要对差分进化算法的各个参数进行合理的设置. 针对不同的优化问题, 参数的设置往往也不同. 另外, 为了使差分进化算法的收敛速度得到提高, 学者们针对差分算法的核心部分, 变异向量的构造形式提出了多种扩展形式, 以适应更广泛的优化问题.
(1)变异因子F
变异因子F是控制种群多样性和收敛性的重要参数. 一般在[0, 2]之间取值. 变异因子F值较小时, 群体的差异度减小, 进化过程不会跳出局部极值, 导致种群过早收敛. 变异因子F值较大时, 虽然容易跳出局部极值, 但是收敛速度会减慢. 一般可选在
(2) 交叉因子
群体的交叉因子
(3) 群体规模M
群体所含个体数量M一般介于5D和10D之间(D为问题的维度), M越大, 种群多样性越强, 获得最优解概率越大, 但是计算时间更长, 一般取20~50.
(4) 最大迭代代数T
最大迭代代数T一般作为进化过程的终止条件. 迭代次数越大, 最优解越精确, 但是计算的时间会越长, 需要根据具体问题设定.
以上四个参数对差分进化算法的求解结果和求解效率都有很大的影响, 因此要合理设定这些参数才能获得较好的效果.
1.4 改进差分进化算法的参数设置对于改进的差分进化算法仅需设定种群规模M和最大迭代代数T两个参数, 减少了人工干预, 有利于模型的应用和推广.
对于机器人轨迹规划中最优轨迹规划的滑模控制问题, 为了将改进DE与标准DE进行对比, 此处的种群规模M和最大迭代次数T的设置与标准DE中相同.
2 基于最优轨迹规划的滑模控制在控制系统的轨迹规划中, 为了使实际上生成的轨迹平滑, 在保持理想轨迹接近参考轨迹的同时, 还应确保系统在运动过程中消耗的总能量尽可能小, 可采用保形分段三次Hermite函数插值, 并结合改进的差分进化方法来进行轨迹规划.
2.1 轨迹规划算法与相关定理考虑机械转动的二阶线性系统
| $I\ddot \theta+b\dot \theta=\tau+d$ | (9) |
其中,
通过差分进化方法, 沿着参考路径进行最优规划, 从而保证系统运动在不偏离参考路径的基础上, 采用滑模控制方法, 实现对最优轨迹的跟踪, 使整个运动过程中消耗的能量最小.
引理1. 对
| $\dot V \leqslant- \alpha V+f,\forall t \geqslant {t_0} \geqslant 0$ |
的解为:
| $V(t) \leqslant {e^{- \alpha (t- {t_0})}}V({t_0})+\int_{{t_0}}^t {{e^{- \alpha (t- \tau)}}f(\tau){\rm{d}}\tau } $ |
其中,
不失一般性, 最优轨迹可在定点运动-摆线运动轨迹的基础上进行优化. 摆线运动的表达式如下:
| ${\theta _r}=({\theta _d}- {\theta _0})\Bigg[\frac{t}{T}- \frac{1}{{2\pi }}{\rm{sin}}(\frac{{2\pi t}}{T})\Bigg]+{\theta _0}$ | (10) |
其中, T是摆线周期;
| ${\theta _r}={\bar \theta _{r,0}},{\bar \theta _{r,1}}, \cdots,{\bar \theta _{r,2n- 1}},{\bar \theta _{r,2n}}$ | (11) |
其中,
| ${\bar \theta _{{\rm{opj}}}}(k)={\bar \theta _{r,j}}+\Delta {\bar \theta _j}(k)$ | (12) |
其中,
最优轨迹能够通过优化与参考轨迹的偏差来间接得到. 假设系统达到稳定的最大允许时间为
| $J=\omega \int_0^{3{T_{\rm{E}}}} | \tau \dot \theta |dt+(1- \omega)\int_0^{3{T_{\rm{E}}}} s (t){\rm{d}}t$ | (13) |
其中,
通过采用差分进化算法, 优化轨迹式(11), 使目标函数值最小, 从而获得最优轨迹. 标准差分进化算法的设定参数如下: 最大迭代次数G, 种群规模M, 变异因子F, 交叉因子cr. 经过差分进化算法可得到一组最优偏差, 进而得到最优的离散轨迹如下:
| ${\bar \theta _{{\rm{op}}}}=[{\bar \theta _{{\rm{op}},{\rm{0}}}},{\bar \theta _{{\rm{op}},{\rm{1}}}}, \cdots,{\bar \theta _{{\rm{op}},{{2n- 1}}}},{\bar \theta _{{\rm{op}},{{2n}}}}]$ | (14) |
为了获得连续型的最优轨迹, 采用保形分段三次Hermite插值进行轨迹规划, 即用保形分段三次Hermite插值的方法对离散轨迹进行插值的边界条件如下:
| ${\theta _{{\rm{op}},{\rm{0}}}}={\mathop \theta \limits^- _{{\rm{op}},{\rm{0}}}}={\theta _0}$ |
| ${\theta _{{\rm{op}},{\rm{T}}}}{\rm{ }}={\mathop \theta \limits^- _{{\rm{op}},{{2n}}}}={\theta _d}$ |
| ${{\bar{\theta }}_{\text{op}}}(0)={{\dot{\bar{\theta }}}_{\text{op},\text{0}}}={{\dot{\theta }}_{0}}=0$ |
| ${{\bar{\theta }}_{\text{op}}}(T)={{\dot{\bar{\theta }}}_{\text{op},2n}}={{\dot{\theta }}_{d}}=0$ |
插值节点为:
| ${\theta _{{\rm{op}}}}({t_j})={\bar \theta _{{\rm{op}},{{j}}}},{t_j}=\frac{j}{{2n}}{T_E},j=1,2, \cdots,2n- 1$ |
将插值得到的连续函数
| $s=\dot e+ce$ | (15) |
其中,
| $\begin{aligned} \dot s &=\ddot e+c\dot e={{\ddot \theta }_{{\rm{op}}}}- \ddot \theta+c\dot e \\ &={{\ddot \theta }_{{\rm{op}}}}- \frac{1}{I}(\tau+d- b\dot \theta)+c\dot e \\ \end{aligned} $ | (16) |
设计滑模控制律为:
| $\tau=b\dot \theta+{\eta _2}sgn(s)+I(c\dot e+{\ddot \theta _{{\rm{op}}}}+{\eta _1}s)$ | (17) |
其中,
定义Lyapunov函数为
| $\begin{aligned} \dot V &=- {\eta _1}{s^2}- \frac{s}{I}(d+{\eta _2}{\rm{sgn}}(s)) \\ &\leqslant- 2{\eta _1}V \leqslant 0 \\ \end{aligned} $ | (18) |
根据引理1中的不等式求解引理[15], 解得
| $V(t) \leqslant V(0){e^{- {\eta _1}t}}$ | (19) |
可见,
考虑简单的被控对象
| $I\ddot \theta+b\dot \theta=\tau+d$ |
其中,
| ${\theta _{{\rm{o}}{{\rm{p}}_{ij}}}}=r({\theta _d}- {\theta _0})+{\theta _0}$ |
其中,
采用改进的差分进化算法设计最优轨迹
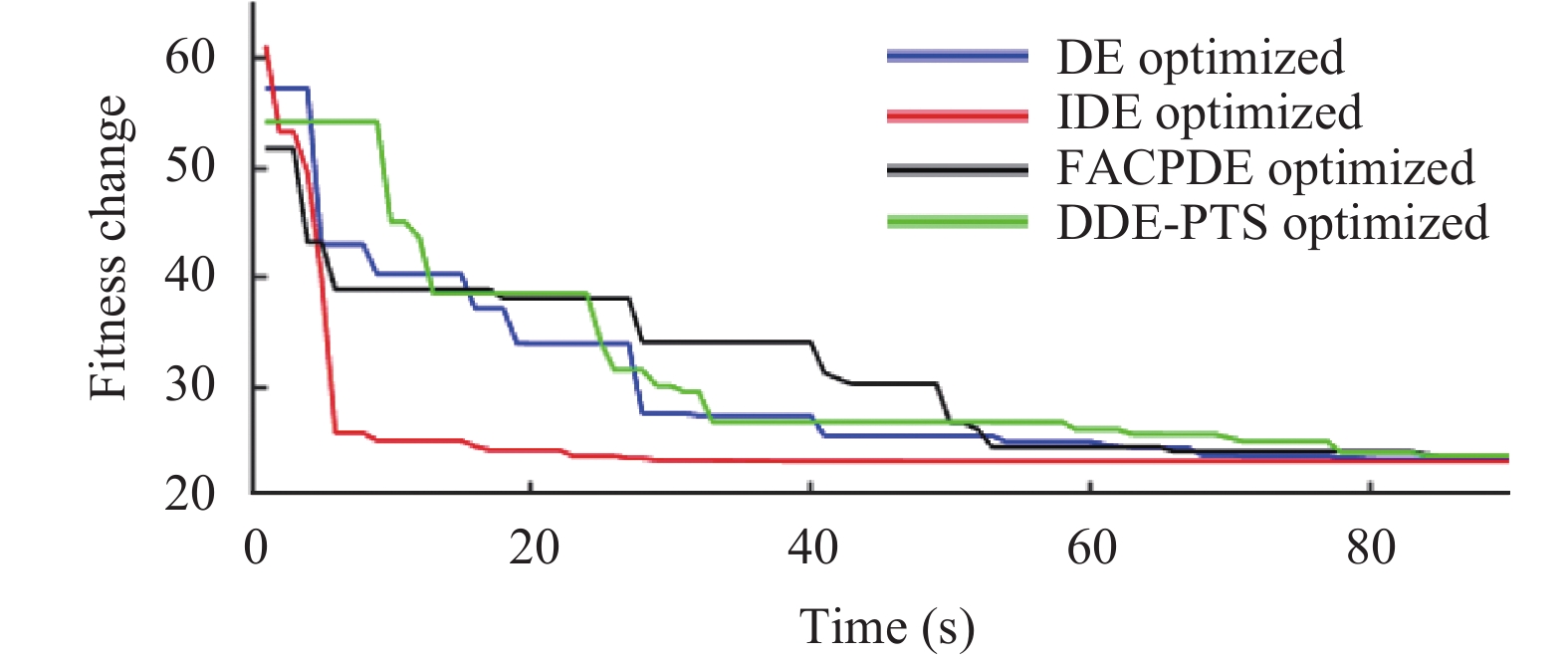
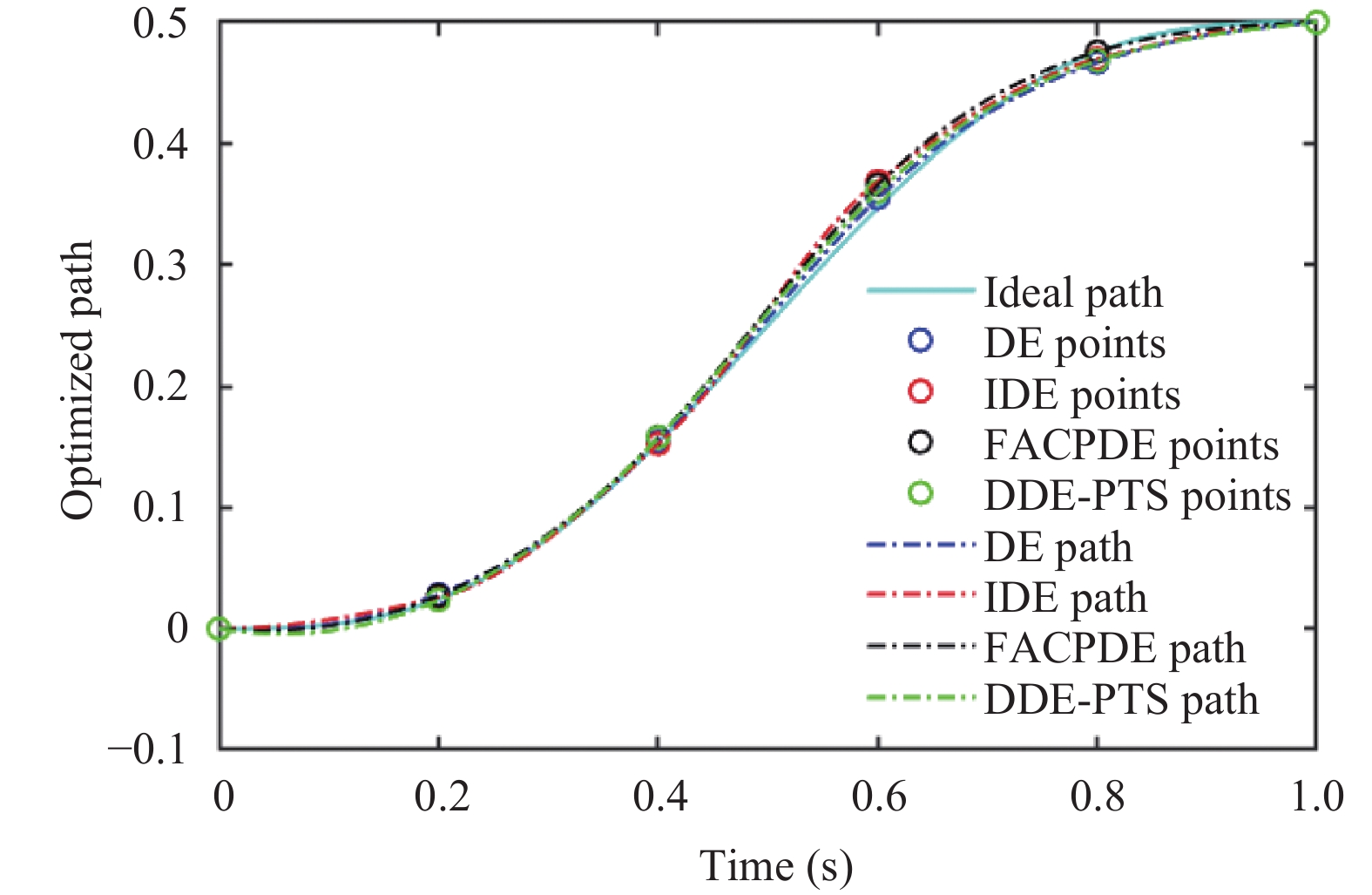
2010年Weber设计了对缩放因子F进行了适应性的调整[16]分布式 DE 算法(FACPDE). 2012年文献[17]提出了对F和C进行动态调整的分布式DE算法(DDE-PTS). 将标准DE, IDE, FACPDE, DDE-PTS与滑模控制相结合, 得到仿真结果如图1~图3所示. 图1为DE与IDE控制输入信号图, 图2为DE FACPDE, DDE-PTS与IDE控制输入信号图. 图1和图2显示了IDE相比DE, FACPDE和DDE-PTS对于消除抖振的效果更佳显著. 标准差分进化算法由于采用了三次样条插值, 要求曲线存在二阶连续偏导, 更加平滑; 由于要解决的问题中存在二阶导数, 改进DE采用保形分段三次Hermite插值, 对于二阶导数仅要求存在, 弱化了条件, 防止了拟合过冲, 使用范围更广. FACPDE, DDE-PTS由于人工参数设置的影响, 导致收敛过程中信号的不稳定性. 从图3的适应度函数曲线和图4的目标函数优化的最优轨迹效果图中, 可以看出, 足够长时间后, DE、FACPDE、DDE-PTS和IDE均可逼近最优解且IDE优化最优轨迹求出最优解的速度比DE,FACPDE和DDE-PTS更快. IDE由于在变异阶段充分利用了群体中最优个体的信息和种群的平均水平, 收敛速度有了很大的提升. 此外, IDE去掉了变异因子和交叉因子, 仅需设置种群数目和最大迭代次数两个参数, 减少了人为参与, 算法的稳定性得到很大程度的提高, 有利于算法的使用和推广. 上述结果验证了IDE算法在轨迹规划方面的合理性和有效性.
5 结论本文研究了机器人的轨迹规划问题, 并提出了基于滑模控制的IDE算法. 该算法在变异阶段充分利用了种群中表现最好的个体和种群中所有个体的信息, 利用表现最好的个体的信息与平均水平的个体的差分引领种群迭代更新的方向, 利用表现最好的个体替换表现最差的个体, 加快了收敛速度. 取消了变异阶段的变异因子和交叉阶段, 去掉了变异因子和交叉因子两个人工调整的参数, 增强了模型的稳定性, 有利于模型发推广应用. 在拟合阶段采用采用保形分段三次Hermite插值, 避免了拟合过冲, 降低了插值函数光滑性的要求, 增大了算法的使用范围.
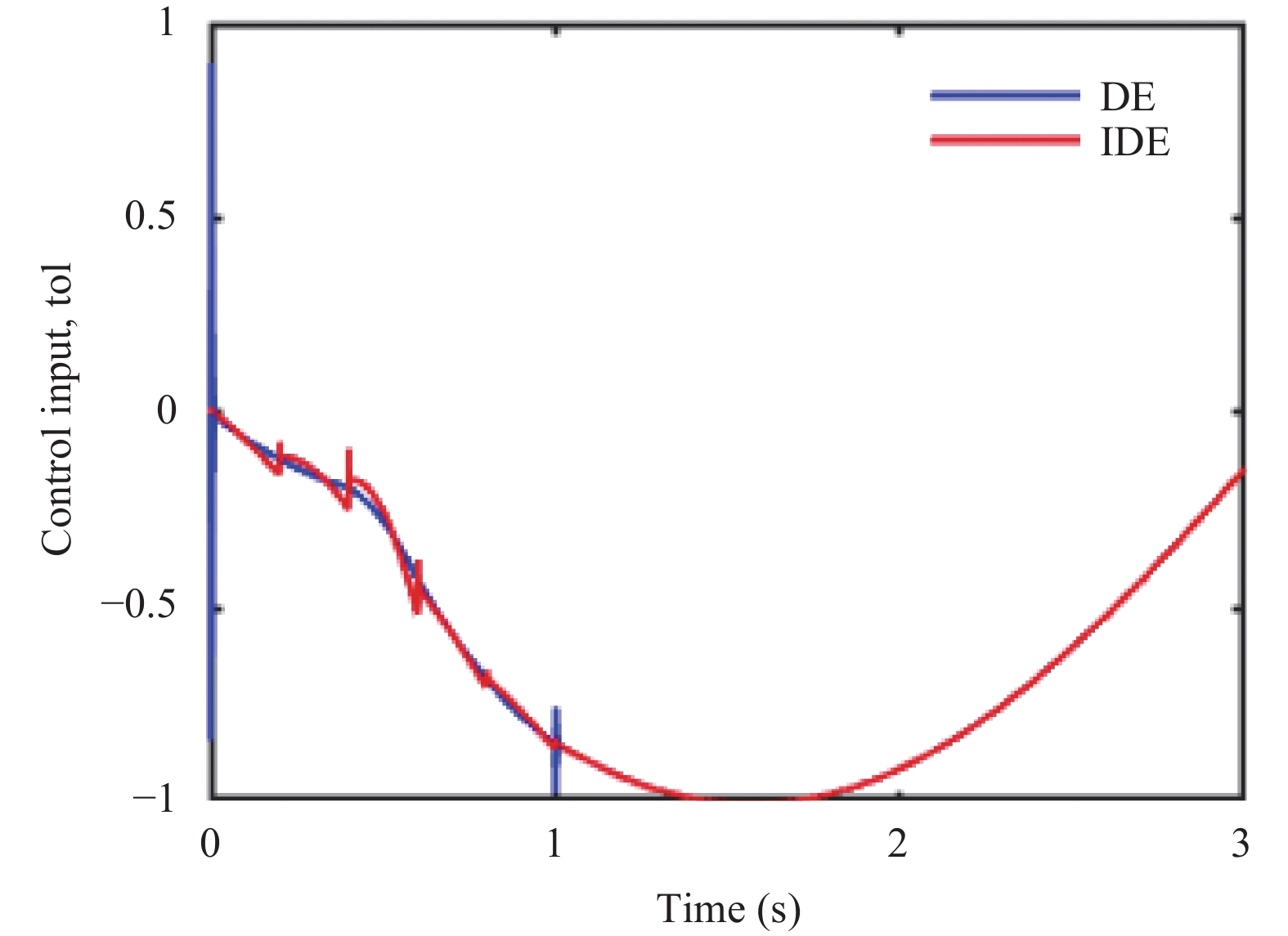
|
图 1 DE与IDE控制输入信号图 |

|
图 2 DE,FACPDE,DDE-PTS与IDE控制输入信号图 |
|
图 3 适应度函数曲线 |
|
图 4 最优轨迹效果图 |
本文工作表明, 所提出的基于滑模控制的IDE算法对于机器人的定点运动-摆线运动轨迹的轨迹规划是有效的, 未来将继续关注IDE算法在其他生产领域的应用研究.
| [1] |
钱东海, 谭伟, 赵锡芳. 基于B样条路径的机器人时间最优轨迹规划. 上海交通大学学报, 1998, 32(12): 29-33. |
| [2] |
杨国军, 崔平远. 机械手时间最优轨迹规划方法研究. 中国机械工程, 2002(20): 1715-1717. DOI:10.3321/j.issn:1004-132X.2002.20.002 |
| [3] |
王宪, 杨国梁. 基于改进蚁群算法的机器人轨迹规划. 计算机系统应用, 2010, 19(11): 79-82. DOI:10.3969/j.issn.1003-3254.2010.11.018 |
| [4] |
甘亚辉, 戴先中. 基于遗传算法的多机器人系统最优轨迹规划. 控制理论与应用, 2010, 27(9): 1245-1252. |
| [5] |
付荣, 居鹤华. 基于粒子群优化的时间最优机械臂轨迹规划算法. 信息与控制, 2011, 40(6): 802-808. |
| [6] |
居鹤华, 付荣. 基于GA的时间最优机械臂轨迹规划算法. 控制工程, 2012, 19(3): 472-477. DOI:10.3969/j.issn.1671-7848.2012.03.026 |
| [7] |
王学琨, 李刚, 周东凯, 等. 基于DE的时间最优6–DOF机械臂轨迹规划算法. 计算机仿真, 2015, 32(8): 332-337. DOI:10.3969/j.issn.1006-9348.2015.08.072 |
| [8] |
余阳, 林明, 林永才. 基于混合遗传算法的工业机器人最优轨迹规划. 计算机工程与设计, 2012, 33(4): 1574-1580. DOI:10.3969/j.issn.1000-7024.2012.04.063 |
| [9] |
赫建立, 朱龙英, 成磊, 等. 基于遗传算法的6–DOF机器人最优时间轨迹规划. 机械传动, 2015, 39(9): 41-45. |
| [10] |
刘一扬, 刘明明. 基于改进遗传算法的机器人运动轨迹跟踪控制. 机械传动, 2016, 40(3): 39-42, 61. |
| [11] |
邓飙, 张潇, 龙勇, 等. 基于五次B样条的起竖装置时间最优轨迹规划. 组合机床与自动化加工技术, 2016(6): 21-25. |
| [12] |
殷凤健, 梁庆华, 程旭, 等. 基于时间最优的机械臂关节空间轨迹规划算法. 机械设计与研究, 2017, 33(5): 12-15. |
| [13] |
梁延德, 李瑞峰, 张红哲, 等. 基于时间最优的PTP轨迹规划问题. 计算机工程与设计, 2017, 38(1): 231-237. |
| [14] |
Das S, Konar A, Chakraborty UK. Two improved differential evolution schemes for faster global search. Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation. Washington DC, USA. 2005. 991–998.
|
| [15] |
Ioannou P, Sun J, Ioannou P A. Robust adaptive controls. Ioannou P, Sun J. Robust adaptive control. Prentice Hall PTR, 2013. 333–335.
|
| [16] |
Weber M, Tirronen V, Neri F. Scale factor inheritance mechanism in distributed differential evolution. Soft Computing, 2010, 14(11): 1187-1207. DOI:10.1007/s00500-009-0510-5 |
| [17] |
Saadi HA, Chouinard JY, Guessoum A. Distributed differential evolution algorithm for PAPR reduction of OFDM signals. Proceedings of the 11th International Conference on Information Science, Signal Processing and Their Applications. Montreal, QC, Canada. 2012. 567–572.
|
 2018, Vol. 27
2018, Vol. 27


