由于农业是国民经济的基础, 而粮食是基础的基础. 粮食不仅是人民群众最基本的生活资料, 也是关系到国家安全的重要战略物资, 我国是人口众多的大国, 解决好吃饭问题始终是治国理政的头等大事^[1]. 因此分析预测我国粮食生产过程的变化规律及其发展趋势, 为实施粮食生产过程的预测和决策、保证国家粮食安全提供理论依据, 具有重要的现实意义.

目前有多种粮食产量的预测方法^[2–5], 例如姚作芳等建立的马尔可夫方法修正的灰色粮食预测模型, 这种方法简便易行, 需要数据少, 可以用于预测粮食产量的变化趋势. 然而, 还需要进一步提高预测精度. 另外, 还有基于线性方法的多元线性回归、时间序列分析等粮食预测模型. 由于, 粮食产量与其多种影响因素之间存在着复杂的非线性依赖关系, 具有不确定性和突变性, 往往线性模型难以适用较长时期预测且预测精度不高. 而人工神经网络模型具有非线性映射能力, 以及较强的鲁棒性和容错性^[6], 因此已被广泛的应用于粮食产量预测问题^[7–9]. 例如吴炎将时间序列分析法和BP神经网络相结合, 建立了江苏省粮食产量预测模型. 这种方法较好的解决了神经网络收敛慢, 但是仍需要改进易于陷入局部极小值的问题. 另一方面, 由于该方法只是利用粮食产量的数据建立模型, 没有考虑影响粮食产量的其他因素, 因而预测精度有待于进一步提高. 且当前的研究大多没有基于粮食产量预测问题为小样本问题这一事实来改进预测模型. BP神经网络由于基于梯度的算法, 存在如低的收敛速度且易陷入局部极小点, 网络训练时对初始连接权值和阈值很敏感等缺陷. 针对BP神经网络的不足,本文拟采用收敛速度快, 具有好的鲁棒性及非常好的全局搜索能力的粒子群算法与BP神经网络相结合, 并针对小样本问题对粒子群算法进行改进. 最终以影响粮食产量的多种因素作为网络输入和粮食产量作为网络输出, 建立了改进粒子群算法(IPSO)与BP神经网络相结合的多因素粮食产量预测模型——IPSO-BP模型. 并与BP网络模型和PSO-BP网络模型进行对比. 结果表明, IPSO-BP模型具有较高精度和算法稳定性, 能够为粮食生产过程的预测和决策提供合理的理论依据.

本文根据1978~2015年《中国统计年鉴》, 选取有效灌溉面积 ${X_1}$ (千公顷)、化肥施用量 ${X_2}$ (万吨)、农村用电量 ${X_3}$ (亿千瓦小时)、农业机械总动力 ${X_4}$ (万千瓦)、农林牧渔业劳动力 ${X_5}$ (万人)、粮食作物播种面积 ${X_6}$ (千公顷)和受灾面积 ${X_7}$ (千公顷)作为影响粮食产量的指标^[10–12](数据见附录1), 作为网络输入, 以粮食产量 $Y$ (万吨)作为网络输出, 构建IPSO-BP神经网络粮食预测模型.

1 IPSO-BP神经网络粮食预测模型的构建

IPSO-BP神经网络预测模型的特点: 用IPSO算法优化BP神经网络的初始连接权值和阈值, IPSO算法结束时能够寻到全局最优附近的点; 在此基础上, 利用局部寻优能力较强的BP算法, 从该点出发进行局部搜索, 进而达到网络的训练目标, 其结合了两种算法的优势, 从而改进了传统BP神经网络的不足.

1.1 改进粒子群算法

粒子群算法(Particle Swarm Optimization)——PSO算法是一种群智能优化算法, 由于其概念简明、收敛较快、实现方便, 被广泛用于调度优化、数据挖掘、神经网络训练、农业工程等方面^[13].

设D维欧氏空间中, 由N个粒子组成群落, 粒子对应位置为 ${x_i} = {({x_{i1}},{x_{i2}}, \cdots ,{x_{iD}})^{\rm{T}}},i = 1,2, \cdots ,N$ , 即问题的可能解. 粒子速度为 ${v_i} = {({v_{i1}},{v_{i2}}, \cdots ,{v_{iD}})^{\rm{T}}}$ ,由其决定粒子的行进方向与距离, 另外速度的每个分量受到最大速度 ${v_m}$ 的限制, 当 ${v_{ij}} > {v_m}$ 时, 令 ${v_{ij}} = {v_m}(1 \leqslant i \leqslant N,1 \leqslant j \leqslant D)$ . 同样 ${x_{ij}}$ 受 ${x_m}$ 的限制, 当 ${x_{ij}} > {x_m}$ 时, 令 ${x_{ij}} = {x_m}$ $(1 \leqslant i \leqslant N,1 \leqslant j \leqslant D)$ . 根据目标函数可以计算粒子在不同位置的适应度. 粒子按下列迭代方法来更新速度和位移:

$\left\{{\begin{array}{*{20}{l}}{v_i^{k + 1} = wv_i^k + {c_1}{r_1}({p_i} - x_i^k) + {c_2}{r_2}({p_g} - x_i^k)}\\{x_i^{k + 1} = x_i^k + v_i^{k + 1},i = 1,2, \cdots ,N}\end{array}}\right.$

(1)

其中 ${p_i} = {({p_{i1}},{p_{i2}}, \cdots ,{p_{iD}})^{\rm{T}}}$ 为第 $i$ 个粒子的个体极值点, 表示第i个粒子在迭代过程中得到其最优适应度时所在的位置. ${p_g} = {({p_{g1}},{p_{g2}}, \cdots ,{p_{gD}})^{\rm{T}}}$ 为全局极值点, 表示全体粒子在迭代过程中所得最优适应度时所在的位置. w为惯性权重系数, 较大的权重有利于提高算法的全局搜索能力,而较小的权重会增强算法的局部搜索能力, ${c_1}$ 和 ${c_2}$ 为学习因子, ${c_1}$ 表示每个粒子受自身个体极值的影响, 使粒子有了足够强的全局搜索能力, 避免局部极小, ${c_2}$ 表示粒子受当前全局极值的影响, 体现粒子间的信息共享. w、 ${c_1}$ 和 ${c_2}$ 共同决定了粒子的空间搜索能力. ${r_1}$ 和 ${r_2}$ 是介于(0, 1)之间的随机数.

然而利用PSO算法优化BP神经网络初始权重时, 也易于陷入局部最优解, 往往得不到所需要的初始权重, 因此在处理BP神经网络小样本训练问题时可能出现不尽人意的结果.

为进一步降低PSO算法陷入局部极值的可能性, 针对不同问题有多种改进粒子群算法——IPSO算法^[14–17]. 其中黄璇提出了一种适用于小样本训练问题的改进方法, 本文借鉴该方法修正了PSO算法中的相关参数, 改进了IPSO-BP神经网络模型^[14]:

$\left\{ {\begin{array}{*{20}{l}}{w = [({w_0} - {w_1})\cos (k/M\pi ) + ({w_0} + {w_1})]/2}\\{{c_1} = {c_{10}} + (k/M)({c_{11}} - {c_{10}})}\\{{c_2} = {c_{20}} + (k/M)({c_{21}} - {c_{20}})}\end{array}} \right.$

(2)

对公式(1)中参数的修正方法如下:

w, k和M分别表示惯性权重系数、当前迭代次数和最终迭代次数, ${w_0}$ 和 ${w_1}$ 为w的初始值和终止值, 且 ${w_0} > {w_1}$ . ${c_1}$ 表示控制粒子趋于局部极值的学习因子, 其初始值为 ${c_{10}}$ , 终止值为 ${c_{11}}$ ; ${c_2}$ 表示控制粒子趋于全局极值的学习因子,其初始值为 ${c_{20}}$ , 终止值为 ${c_{21}}$ . w依赖于余弦函数变化的策略在于: w在迭代次数k由0到M的过程中由 ${w_0}$ 递减到 ${w_1}$ , 即迭代初期注重全局搜索, 迭代后期加强了局部搜索, 减小了过早落入局部寻优的可能, 且w依赖于余弦函数变化时, 迭代的前期和后期w的下降速度慢, 使得迭代初期能快速全局寻优且持续较长时间, 进一步减小了过早地陷入局部寻优的可能, 在迭代后期可以较为平缓地进行精细搜索. 对 ${c_1}$ 、 ${c_2}$ 的改进策略在于: ${c_1}$ 随着迭代次数k以线性方式递减, ${c_2}$ 则以线性方式递增. 由此 ${c_{10}}$ 大于 ${c_{11}}$ , ${c_{20}}$ 小于 ${c_{21}}$ . 并且 ${c_{10}}$ 大于 ${c_{20}}$ , ${c_{11}}$ 小于 ${c_{21}}$ , 即迭代初期侧重于自身认知, 末期侧重于全局认知, 从而保证粒子对自身认知能力和全局认知能力的合理动态控制.

1.2 IPSO算法优化BP神经网络的初始权重和阈值

IPSO-BP算法流程如下:

① IPSO算法所需参数和神经网络结构的确定

IPSO算法所需参数包括种群规模N, 粒子维度D, 最终迭代次数M, 惯性权重系数w的初始值和终止值 ${w_0}$ 、 ${w_1}$ , 学习因子的初始值 ${c_{10}}$ 、 ${c_{20}}$ 和最终值 ${c_{11}}$ 、 ${c_{21}}$ , 最大速度 ${v_m}$ ; BP神经网络采用三层网络结构, 每个粒子需包含全部的权值和阈值, 即输入层与隐层、隐层与输出层的连接权重以及输出层和隐层的阈值. 因此, 粒子的维度D应为:

$D = {D_{in}}{D_h} + {D_h}{D_{out}} + {D_h} + {D_{out}},$

(3)

式中, ${D_{in}}$ 、 ${D_h}$ 、 ${D_{out}}$ 分别为输入层、隐层和输出层的节点数.

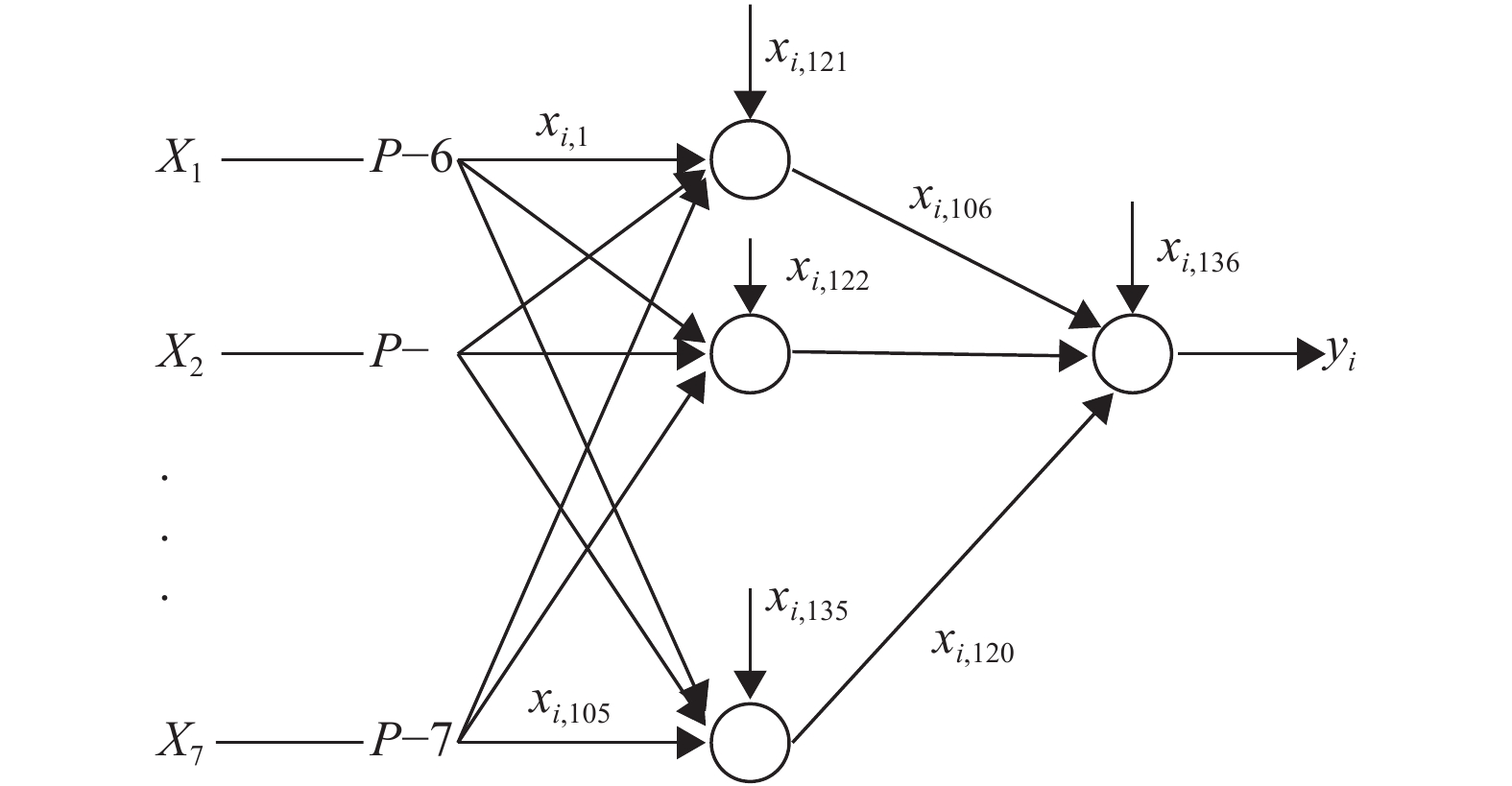
对于粮食产量预测问题, 7个影响因素对应输入层7个节点, 网络输出为粮食产量, 因此输出层节点数为1, 隐层有15个节点. 如图1所示.

维度D=136包含120个权值和16个阈值. 对每一个粒子其位置 ${x_i} = {({x_{i1}},{x_{i2}}, \cdots {x_{iD}})^{\rm{T}}}$ 的第1个到105个分量、第106个到120个分量分别对应一个15×7、1×15的隐层的权重矩阵和输出层的权重矩阵, 第121个到135个分量、第136个分量分别对应隐层节点和输出层节点的阈值向量.

② 适应度函数的确定

初始化BP神经网络, 并将神经网络的实际输出和理想输出的均方差作为适应度函数:

其中X为网络的输入, 即影响粮食产量的七个指标,采用38组数据训练和测试网络, ${y_i}$ 、 $y_i'$ 分别为网络训练的粮食输出值和实际粮食产量.

③ 迭代更新

$\left\{ {\begin{array}{*{20}{l}}{F(X,{x_i}) = {{({y_i} - y_i')}^2},i = 1,2, \cdots ,N}\\{X = ({X_1},{X_2}, \cdots ,{X_7})}\end{array}} \right.$

(4)

在IPSO优化阶段, 在利用式(1)迭代时, 利用式(4)计算每个粒子的适应度值 $F(X,{x_i})$ , 若 $F(X,{x_i}) < F({p_i})$ ,则 ${p_i} = {x_i}$ ,若 $F(X,{x_i}) < F({p_g})$ , 则令 ${p_g} = {x_i}$ , 若上面两等式同时成立, 则 ${p_g} = {p_i} = {x_i}$ ; 然后根据公式(2)更新粒子的惯性权值系数w和学习因子 ${c_1}$ 、 ${c_2}$ , 再利用式(1)对位置 ${x_i}$ 和速度 ${v_i}$ 进行更新, 同时需保证 ${x_{ij}} \in [ - {x_m},{x_m}]$ , 且 ${v_{ij}} \in [ - {v_m},{v_m}]$ . 更新后, 重新计算每个粒子的适应度 $F(X,{x_i})$ ,并根据 $F(X,{x_i})$ 更新 ${p_i}$ 和 ${p_g}$ 的取值. 重复迭代操作, 直至满足k=M, 从而获得最优解.

此时的全局极值点 ${p_g}$ 即为最优解, 由此作为BP神经网络的权重和阈值进行训练粮食预测模型.

2 基于IPSO-BP神经网络的粮食产量预测 2.1 IPSO-BP神经网络模型的粮食产量预测

为了减小不同因子之间由于数据大小的差异和量纲的不同所引起的误差, 在学习之前采用MATLAB中自带函数mapminmax对原始数据进行归一化处理.

本实验采用MATLAB R2014a神经网络工具箱进行测试实现^[18], 从样本数据中随机抽取30组作为训练数据, 剩余8组 $({m_i} = 1,2, \cdots ,8)$ 作为测试数据. 采用IPSO-BP神经网络模型的算法, 经测试, 确定参数N=70, M=50, ${w_0} = 1$ , ${w_1} = 0.1$ , ${c_{10}} = 2.5$ , ${c_{11}} = 1.25$ , ${c_{20}} = 0.5$ , ${c_{21}} = 2.5$ .

IPSO-BP神经网络模型预测结果如表1和图2所示.

由表1和图2可见, 基于IPSO-BP神经网络建立的预测模型对粮食产量的预测结果较为准确, 说明这种粒子群算法的改进方法比较适合粮食产量预测问题.

2.2 IPSO-BP神经网络模型与其他方法预测精度对比

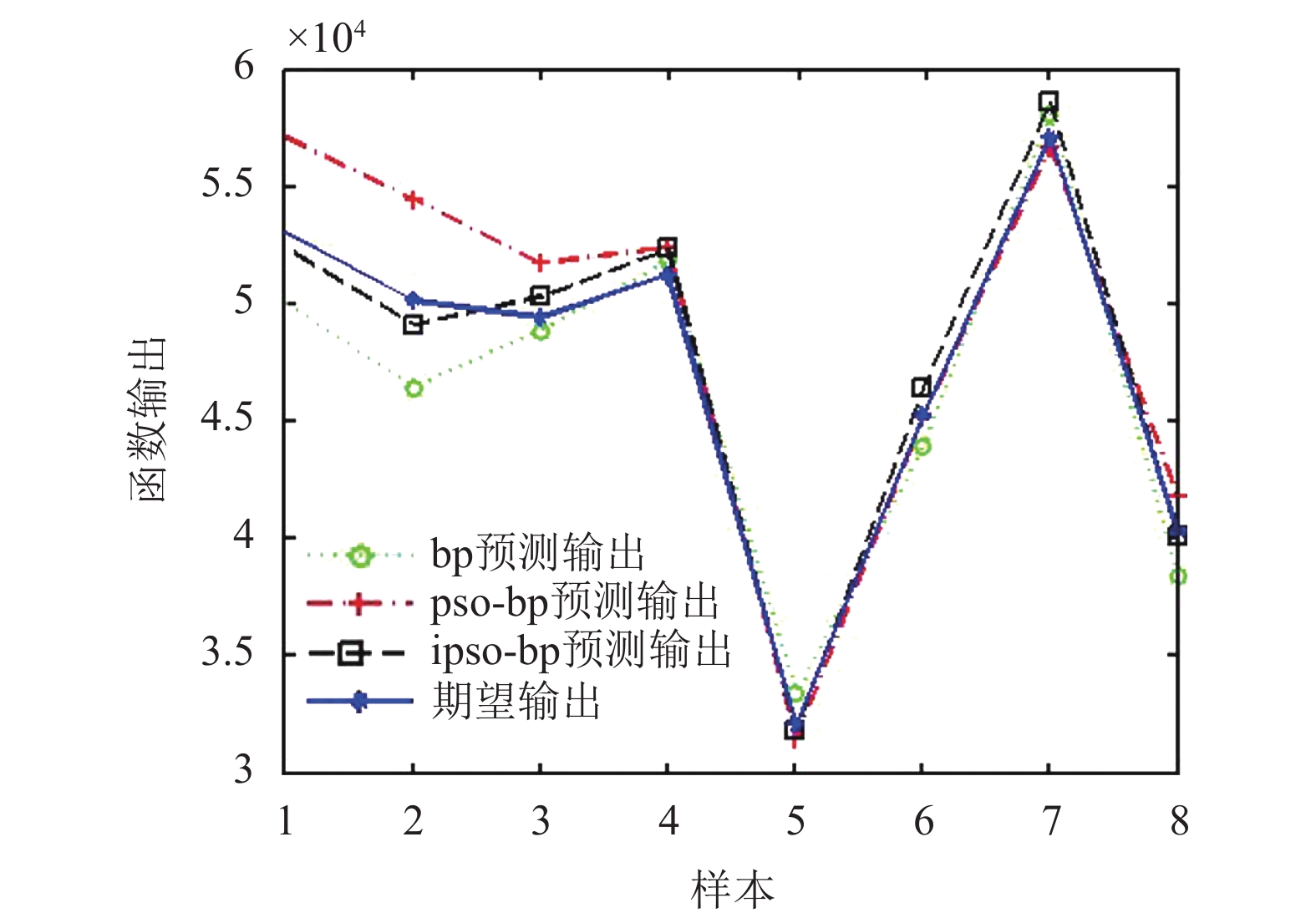
为了验证IPSO-BP神经网络对粮食产量预测精度的提升效果, 本文重新选取了30组数据, 分别建立了BP神经网络和PSO-BP神经网络来对粮食产量进行预测. IPSO-BP神经网络模型与BP神经网络模型及PSO-BP神经网络模型预测结果比较见图3.

此时BP神经网络、PSO-BP神经网络、IPSO-BP神经网络的预测输出相对误差如表2所示.

由表2可见, BP神经网络预测相对误差保持在0.0170到0.0800之间, 平均值为0.0375, PSO-BP神经网络预测相对误差保持在0.0021到0.0800之间,平均值为0.0355, 相比之下, IPSO-BP神经网络预测相对误差保持在0.0041到0.0250之间, 平均值为0.0170.

很明显, IPSO-BP神经网络预测结果的精度和稳定性大幅提高, 预测结果的相对误差基本可以保持在0.02左右,有时可达到0.005以下.

由于样本数量少且样本数据维度较大, 易出现过拟合现象, 使预测模型的泛化能力不强. 考虑到样本数量较少, 因此可用留一法交叉验证对三种模型进行评估. 结果见图4.

由上图可知, 在留一法交叉验证中, IPSO-BP神经网络预测值的相对误差在38次测试中保持在0.000 15—0.000 82之间; 而PSO-BP神经网络的预测结果相对误差大部分保持在较低水平, 但存在数个较高的误差; BP神经网络预测结果则误差很大, 且波动较大.

由以上结果可以得出, 对于相同的样本数据, IPSO-BP神经网络比BP神经网络和PSO神经网络具有更高的预测精度, 且经过留一法交叉验证可验证, IPSO-BP神经网络的预测输出不但比其他两种方法精度高, 而且算法具有较高稳定性, 说明IPSO-BP神经网络有很强的的泛化能力.

3 结语

本文根据粮食产量预测问题的特点, 用合适的方法改进粒子群算法, 并综合考虑粮食产量影响因素, 构造适合粮食产量预测的模型, 提高了粮食产量的预测精度. 同时本模型对粮食产量的长期变化趋势预测能力偏弱, 还需进行进一步研究. 但总体来说本文提出的IPSO-BP神经网络模型可以较好的用于我国粮食产量预测问题, 为制定粮食政策与实施粮食生产系统控制提供决策依据和理论支持.