随着信息时代的进步, 科学技术尤其是电子技术、计算机技术的飞速发展, 各种系统及设备的性能大大提高, 其结构也变得越来越复杂, 导致系统呈现出多种失效模式, 给系统的可靠性分析带来了新的问题.
故障树分析方法(Fault Tree Analysis, FTA)在六十年代初由美国贝尔研究所提出, 并用于民兵导弹的控制系统设计, 为预测导弹发射的随机失效概率做出了贡献. 目前, FTA已广泛应用于电子、电力、化工、机械、交通乃至土木建筑领域的关键系统定量或定性失效分析中. FTA通过分析系统潜在的薄弱环节, 建立故障树模型, 为那些能够导致系统失效的事件组合提供了数学和图表的表达方法. 但随着容错系统的大量应用, 动态逻辑门的引入, 传统的基于最小割集(Minimal Cut Set, MCS)的故障树可靠性理论和方法必须加以修正才能全面描述和反映动态故障树的特性[1,2]. 越来越多的系统, 例如计算机服务器系统、电信系统、水、气以及配电系统等都要求有容错功能, 即在发生故障时, 这些系统仍保持在可接受的或性能下降一级开展工作. 近年来, 人们逐渐将决策图引入故障树分析和复杂系统容错功能的分析与设计中[3,4].
本文通过对边值多值决策图和其相关决策图的介绍, 以及边值多值决策图在动态故障树分析中的应用, 对边值多值决策图进行了全面深入的分析阐述. 本文组织结构如下: 第2节介绍了二叉决策图、多比特函数二叉决策图和多比特边值二叉决策图的基本知识并列举了实例进行分析; 第3节通过具体实例对多值函数、多值决策图和边值多值决策图进行了介绍; 第4节以网络计算系统为例说明了边值多值决策图在动态故障树分析中的应用, 并分析了其性能; 第5节对边值多值决策图进行了总结.
2 边值二叉决策图 2.1 二叉决策图二叉决策图(Binary Decision Diagram, BDD)采用有向无环图表示从{0,1}n到{0,1}映射的布尔函数
二叉决策图可以根据香农展开定理, 对布尔函数
例如: 对于布尔函数
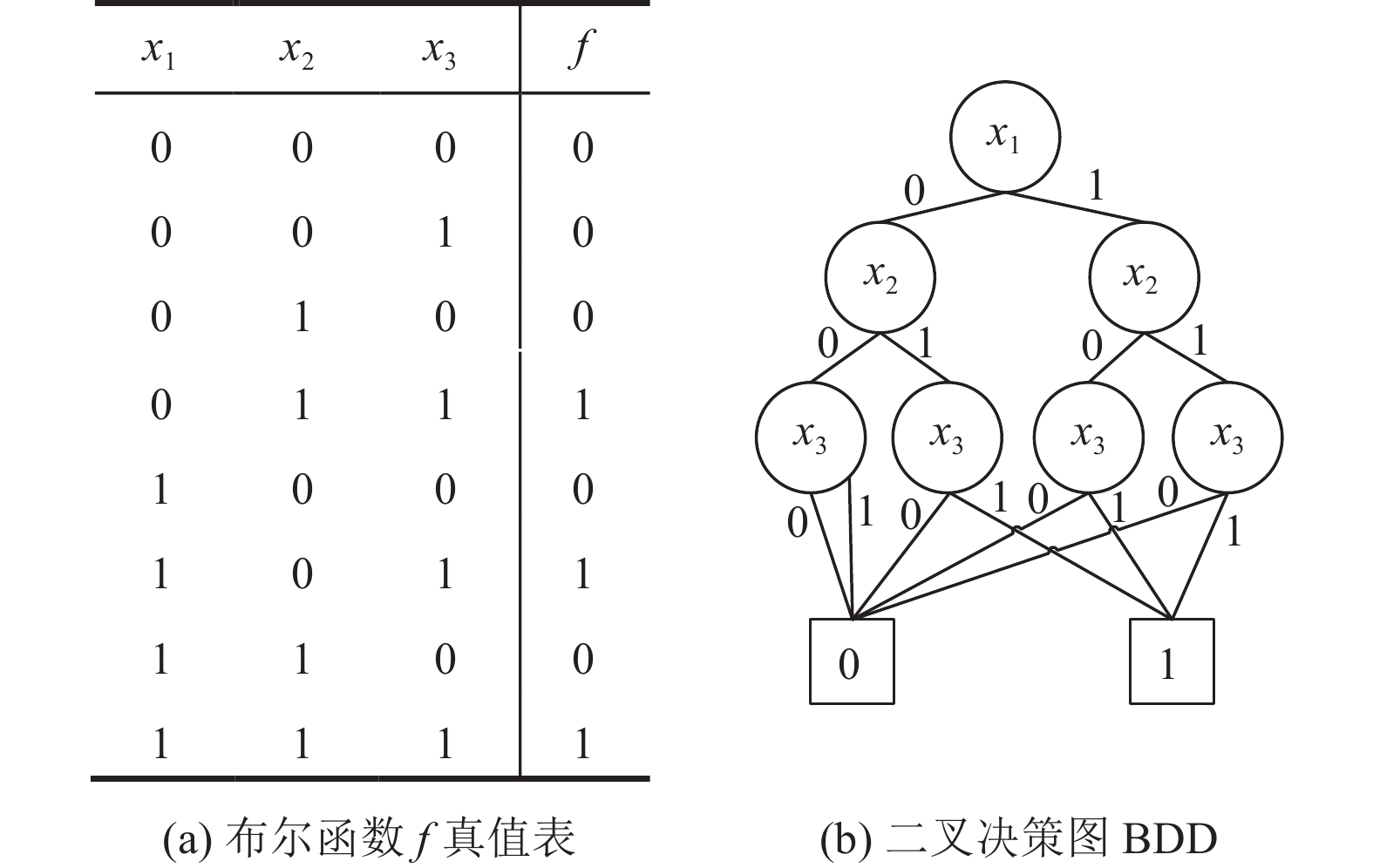
二叉决策图(b)中0、1两个终节点分别代表f的0和1两个取值; xi下方的两条分支分别表示xi取值为0的0-边和xi取值为1的1-边 .
二叉决策图适用于具有两个对立状态的系统性能的判断[10]. 例如图1中的终点0和1分别表示系统无故障和有故障.
2.2 多比特函数二叉决策图多比特函数二叉决策图是对二叉决策功能的扩展, 多比特函数的每个变量由多位二进制数表示, 而布尔函数的每个变量都是用一位二进制数来表示. 下面对多比特函数的二叉决策图进行举例说明.
|
图 1 布尔函数f和f的二叉决策图 |
表1(a)为sinX函数值表, 假设我们选择3 bit的二进制数来表示X和sinX, 则取递增单位为1/23=0.125, 采用就近取整原则, 可得二值化后的函数如表1(b)所示.
| 表 1 sinX函数 |
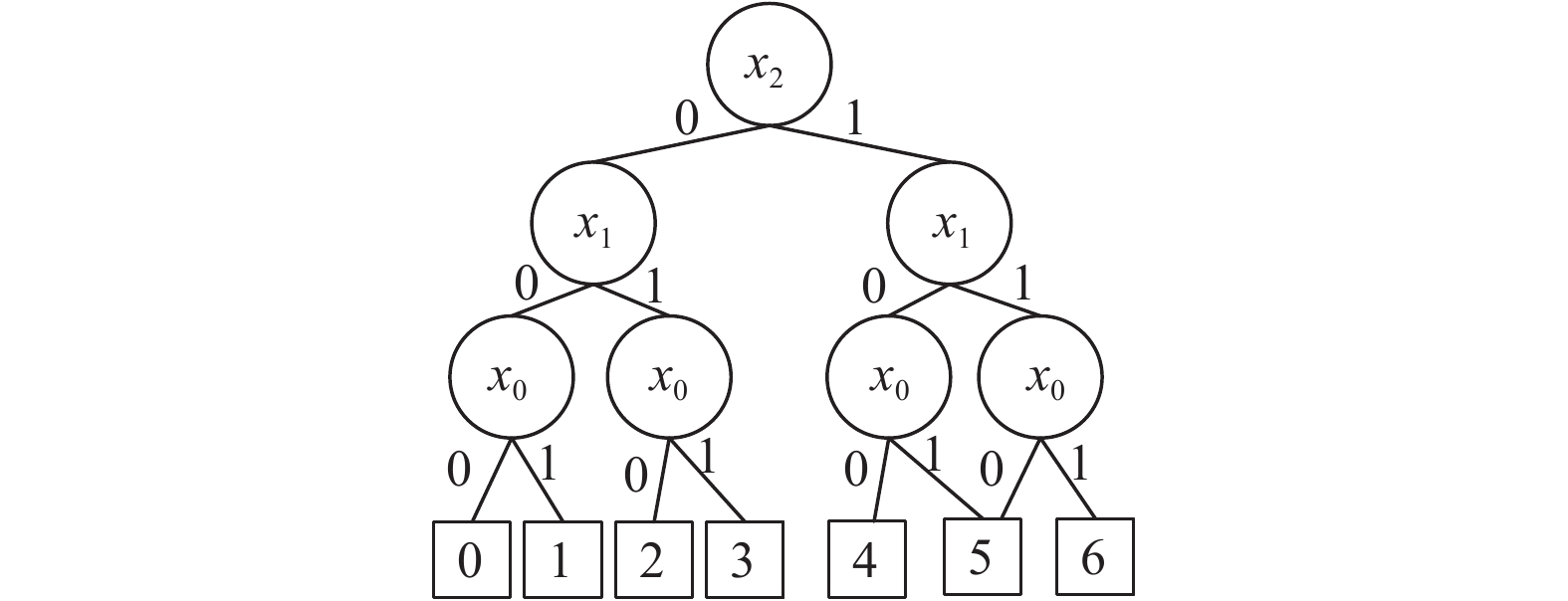
表1(b)的二叉决策图如图2所示. 节点X0、X1和X2分别表示变量X的3个bit位, X0是最低位, X2是最高位. 虚线边表示Xi的0-边, 即Xi取值为0; 实线边表示Xi的1-边, 即Xi取值为1. 终节点表示函数的输出结果.
多比特函数的输出结果是由多位二进制数表示[11], 即有多种输出结果. 多比特函数二叉决策图适用于对多状态且每个系统组件只有两个状态的系统进行表示. 例如图2中的7个终节点对应系统的7种不同运行状态, 而系统内各组件只有0和1两个状态, 对应组件的有故障和无故障状态.
2.3 多比特函数边值二叉决策图边值二叉决策图(Edge-Value Binary Decision Diagram, EVBDD)是BDD的变体, 表示整数值函数. EVBDD仅由一个表示0的终节点和具有整数权重边的内部节点组成. EVBDD边值求解规则如下:
(1) 所有节点0-边总是具有零权重, 即0-边的边值为0.
(2) 节点1-边的边值为当其子节点取值为0且其它节点取值相同, 该节点取值为1时的函数值与取值为0时的函数值之差. 即节点xi的1-边的边值e为:
| $ \begin{aligned}e = & f\left( {{x_1}, \cdots ,{x_{i - 1}},1,0,{x_{n + 2}},\cdots,{x_n} } \right)\\& - f\left( {{x_1}, \cdots ,{x_{i - 1}},0,0,{x_{n + 2}},\cdots,{x_n} } \right)\end{aligned} $ |
|
图 2 二叉决策图BDD |
|
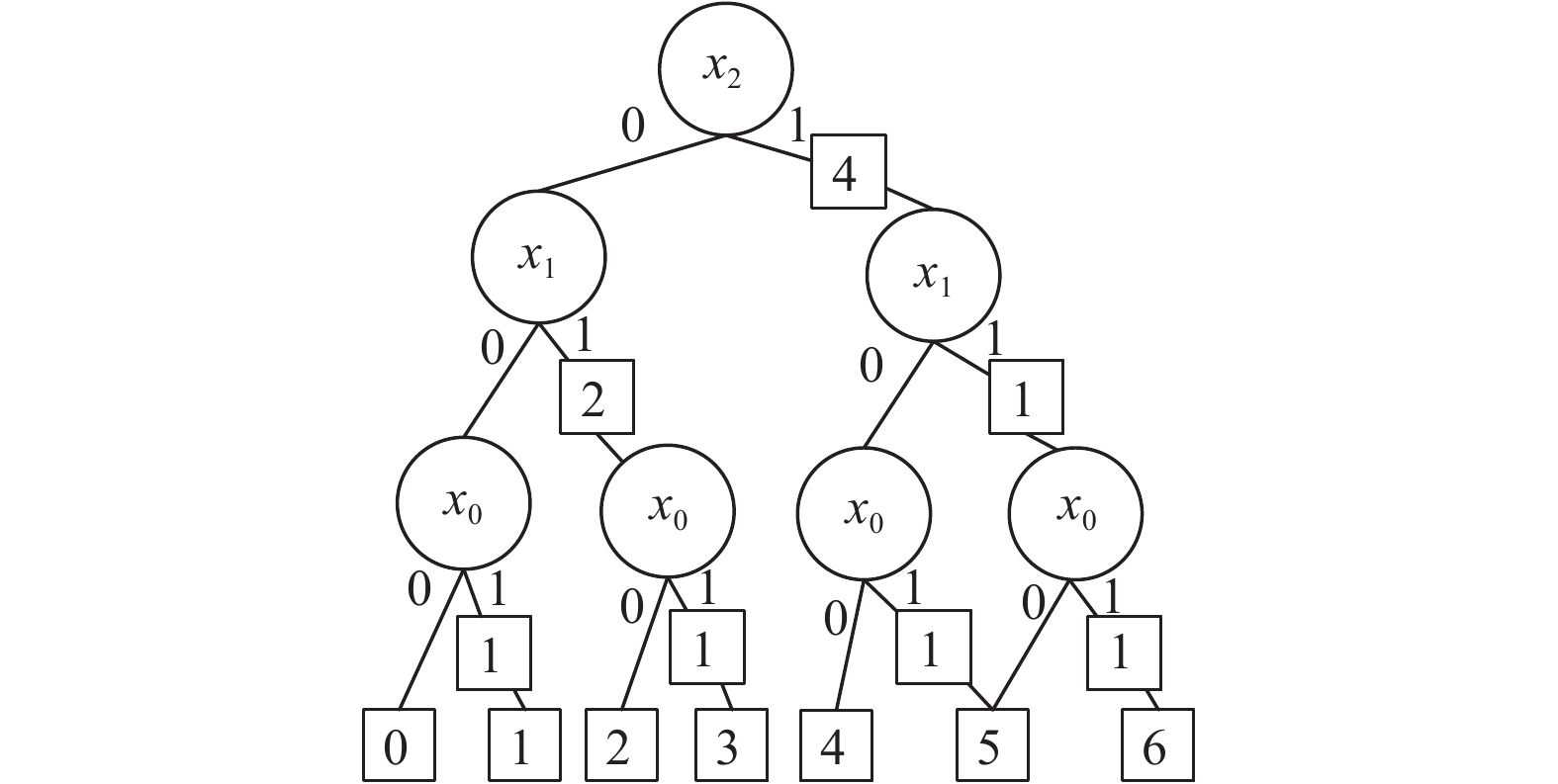
图 3 sinX的边值二叉决策图EVBDD |
边值相加即可得到函数的最终输出结果. 例如X21-边的边值, 可以用X2X1X0=100时的输出100减去X2X1X0=000的输出000, 结果等于4, 即X2的1-边的边值为4.
为便于系统状态的计算, 可以对边值二叉决策图进行缩减, 去掉冗余节点, 简化搜索路径. 冗余节点的定义如下: 若边值二叉决策图的两个或两个以上同名节点的0-边或1-边均指向相同的分支子节点, 或均指向终节点, 且1-边的边值相同, 则此同名节点存在冗余. 缩减规则:
(1) 对边值二叉决策图由下至上进行递归判断, 判断是否存在冗余节点;
(2) 对存在冗余的同名节点, 保留一个节点即可, 直至边值二叉决策图中不再存有冗余节点.
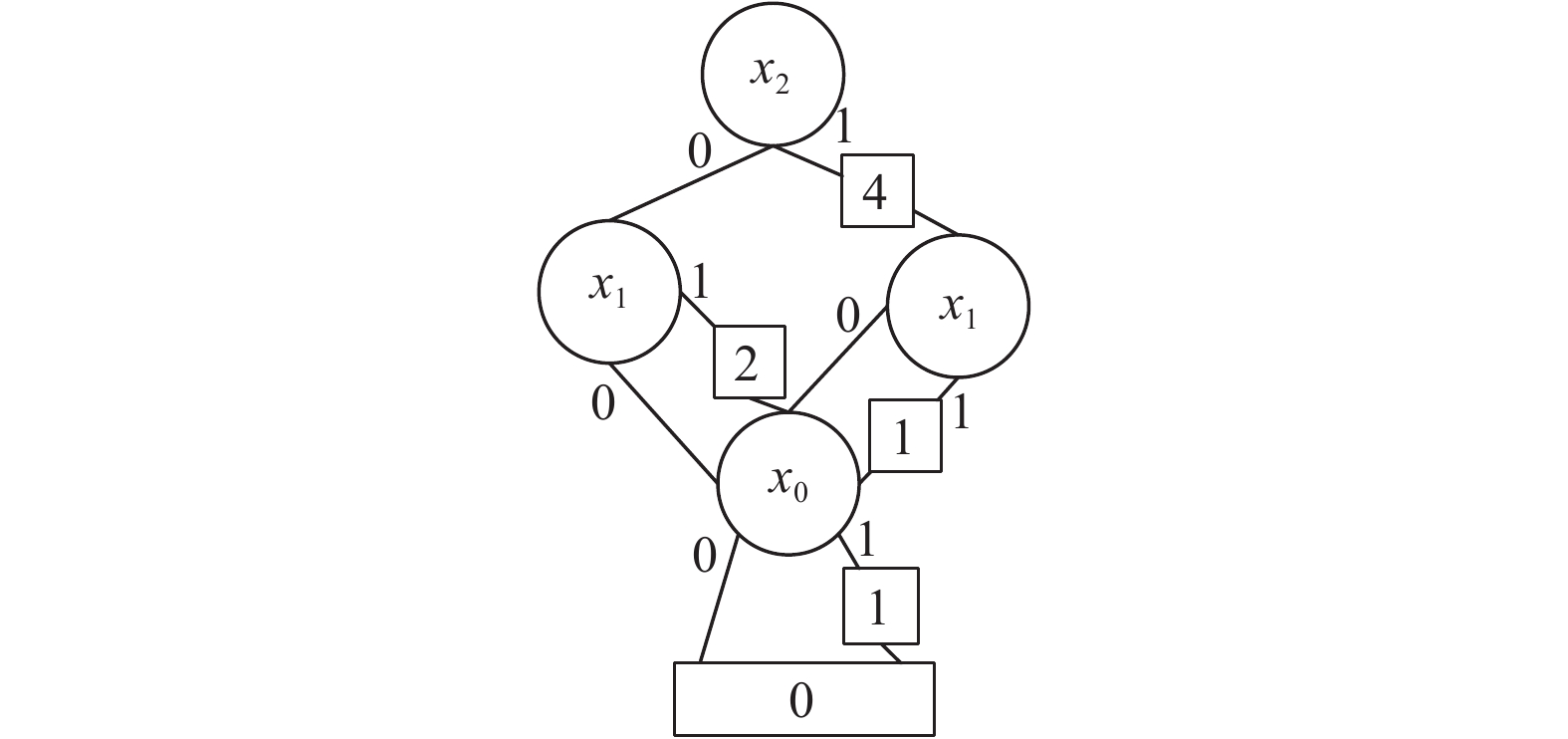
缩减后的二叉决策图的函数输出结果由边值的和计算获得, 所以终节点由0来表示[11]. 图3的缩减边值二叉决策图如图4所示. 图3中四个X0的1-边的边值完全相同, 且均指向终节点, 所以可以删除其它三个X0节点.
多比特函数边值二叉决策图的应用类似于多比特二叉决策图, 区别在于系统最终状态由边值的和来表示.
|
图 4 缩减后的边值二叉决策图EVBDD |
3 边值多值决策图 3.1 多值决策图
如前所述, 当系统的状态多于2个时, 我们称系统为多态系统. 若系统中的各个组件也具有多个状态时, 我们称系统为具有多状态组件的多态系统, 简称为多态系统. 文献[3]指出多态系统的性能、容量或系统的状态可靠性级别都可以用系统的状态来表示.
多态系统的状态仅仅依赖系统组件的状态. 含有n个组件的系统可以被认为是一个多值函数
| $ \begin{array}{l}f({x_1},{x_2}, \cdots ,{x_{{\rm{i}} - 1}},\alpha ,{x_{i + 1}}, \cdots ,{x_{n }}) \le \\f({x_1},{x_2}, \cdots ,{x_{i - 1}},\beta ,{x_{i + 1}}, \cdots ,{x_{n }})\\\alpha ,\beta \in {R_i},{\text{且}}\alpha \le \beta . \end{array} $ |
可以定义当xi取值为0时, 为组件的最坏状态即组件完全故障, 当xi取值为ri–1时, 为组件的最佳状态即组件完全无故障; 当f的值为0时, 为系统的最坏状态即系统完全故障, 当f的值为m–1时, 为系统的最佳状态即系统完全无故障. 随着组件状态值的增加, 系统的状态值也增加, 即组件的故障越少, 系统的故障就越少, 运行状态就越好.
多值决策图(Multiple-valued Decision Diagrams, MDD)是反映部件状态与系统状态之间关系的有向无环图. MDD的获得与BDD的获得类似, 通过香农展开定理, 重复应用于多值函数的各个组件获得. MDD的内部节点表示通过向某些组件赋值从而获得的f的子函数, 每个内部节点具有对应于组件值的多个输出边[3]. 例如对于多值函数
| $ \begin{array}{l}{f_0}\left( {{x_1},{x_2},{x_3}} \right) = {x_1} + {x_2} + 2{x_3},\\{x_1}\left( {0,1,2} \right),{x_2}\left( {0,1,2} \right),{x_3}\left( {0,1} \right). \end{array} $ |
| $ f = \left\{ \begin{array}{l}0,{\rm{ }}{f_0} = 0\\1,{\rm{ }}{f_0} \in \left[ {1,2} \right]\\2,{\rm{ }}{f_0} \in \left[ {3,4} \right]\\3,{\rm{ }}{f_0} \in \left[ {5,6} \right]\end{array} \right. $ |
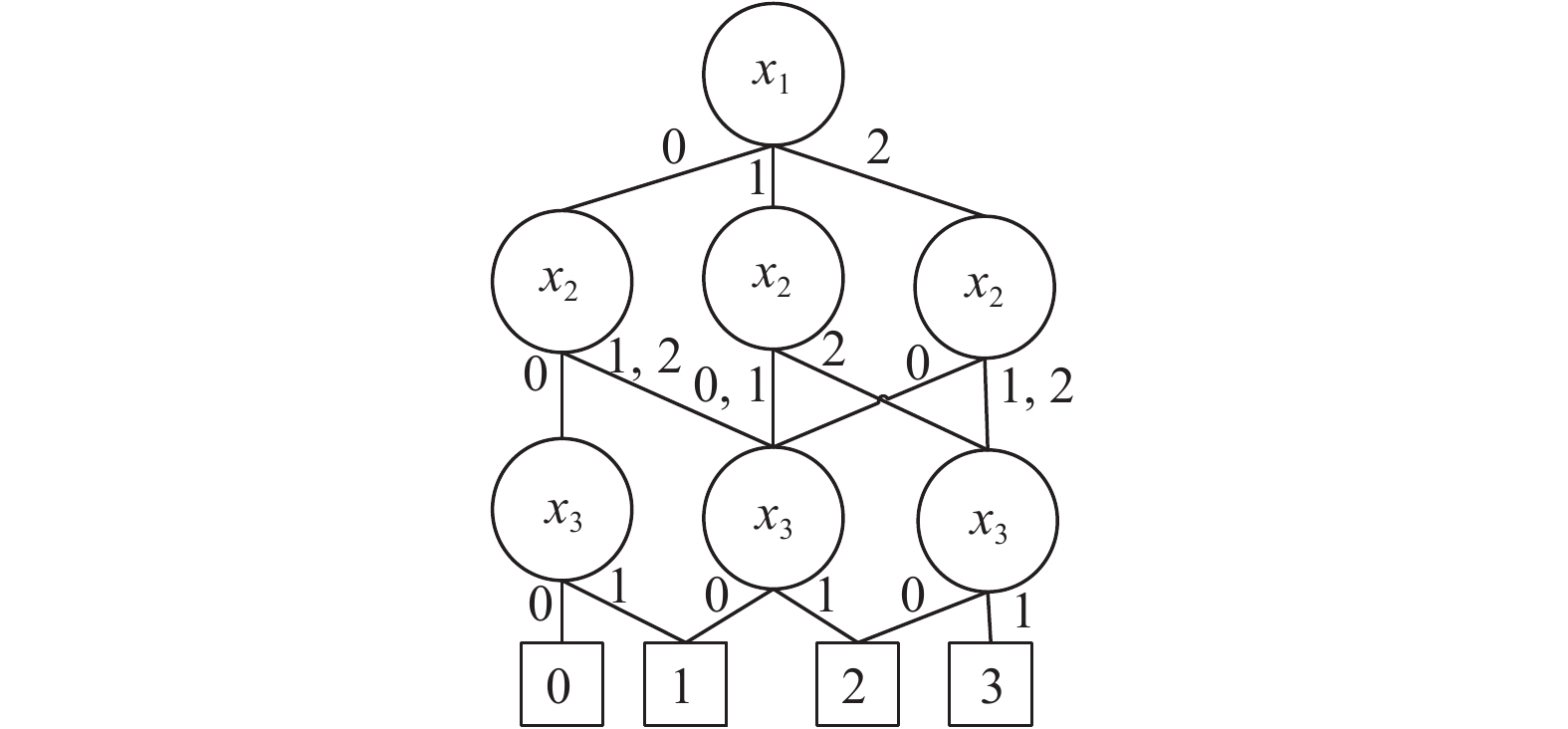
由以上的多值函数f得到的取值表如表2所示, 图5为其决策图, 图中的终节点0, 1, 2, 3分别表示多值函数f的取值.
| 表 2 多值函数f的取值表 |
3.2 边值多值决策图
边值多值决策图(Edge-Value Multiple-valued Decision Diagram, EVMDD)是多值决策图的扩展, 它包括表示0的一个终节点和具有整数权重边值的内部节点; 0-边总是具有零权重. 在EVMDD中, 函数值被表示为从根节点遍历到终节点的边值的和[3,12,13].
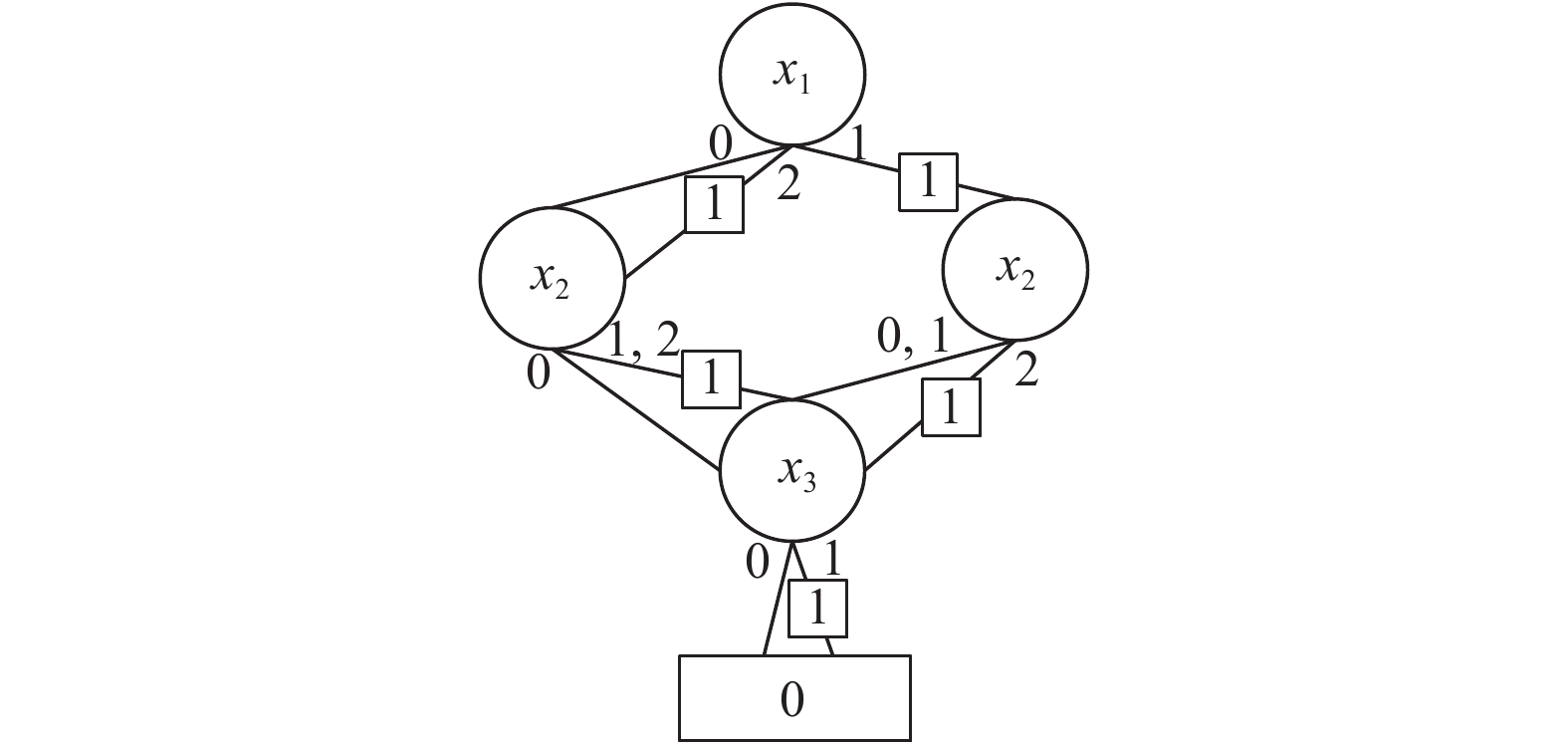
以图5为例, 使用与边值二叉决策图相同的边值求解和缩减规则得到的多值函数f的边值多值决策图如图6所示. 因为x2的分支子节点x31-边的边值完全相同, 所以可以合并. x1的0-边的分支子节点x2和2-边的分支子节点x2的边值相同, 所以进行合并. x1的1-边分支子节点x2与其它边的分支子节点x2的边值不相同, 所以不能缩减.
经过比较, 发现MDD有7个节点, 而EVMDD只有4个节点, 减少了3/7. 文献[3]中提到计算的时间复杂度与决策图中的节点数量成正比, 所以在计算的时间复杂度方面, EVMDD比MDD更有优势.
|
图 5 多值函数f的MDD |
|
图 6 多值函数f的EVMDD |
4 案例研究 4.1 高度可靠的网络计算系统
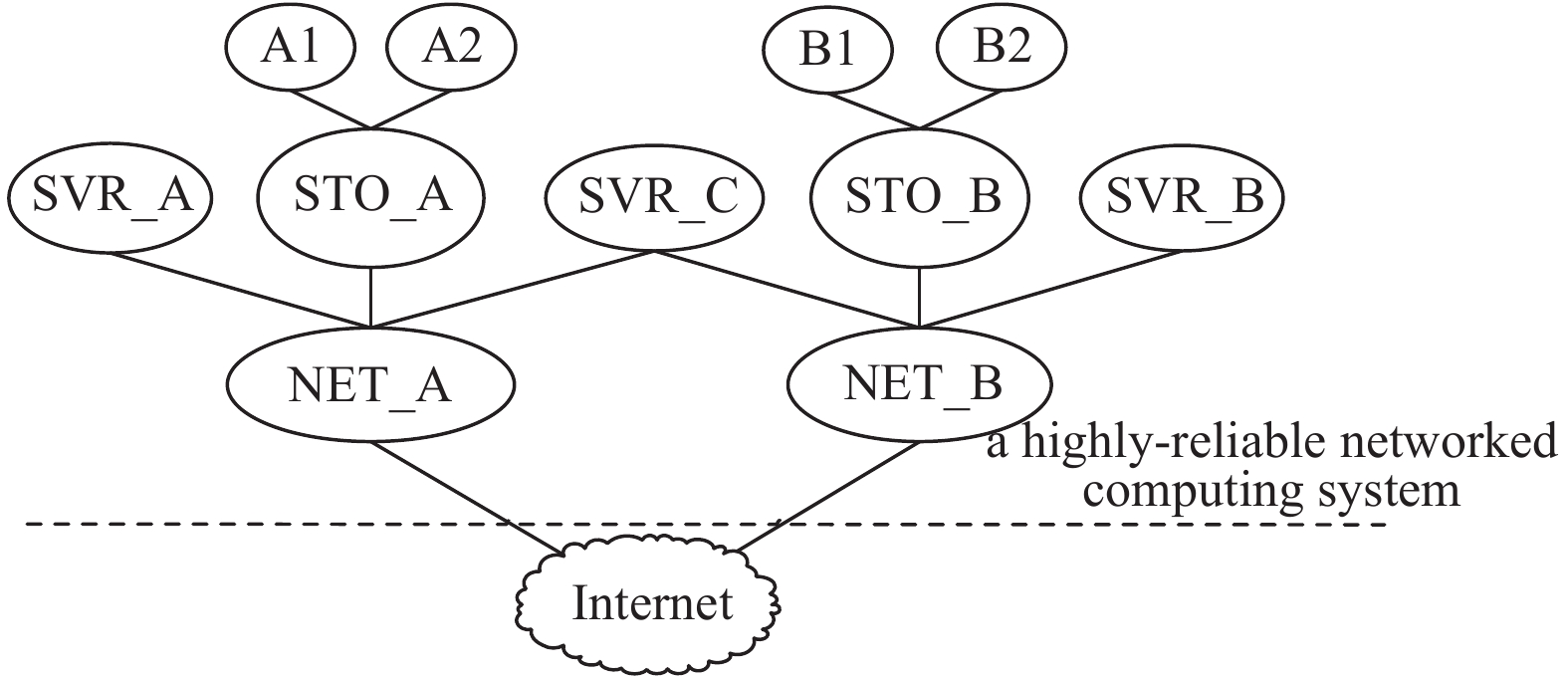
以文献[14]中提到的高度可靠的网络计算系统为例, 系统架构如图7所示, 通过两个不同的数据进程提供网络计算服务. 系统分为两个部分, Complex A和Complex B. 每个子系统包含一个服务器(SVR)、一个存储子系统(STO)及一个网络子系统(NET). 存储子系统采用镜像存储方式, 包含一个存储控制器及两个存储空间. 当存储控制器故障时, 该存储控制器故障. 备用服务器SVR_C作为失效备援, SVR_C和两个服务器SVR_A、SVR_B间采用心跳连接.
|
图 7 高可靠性网络计算系统 |
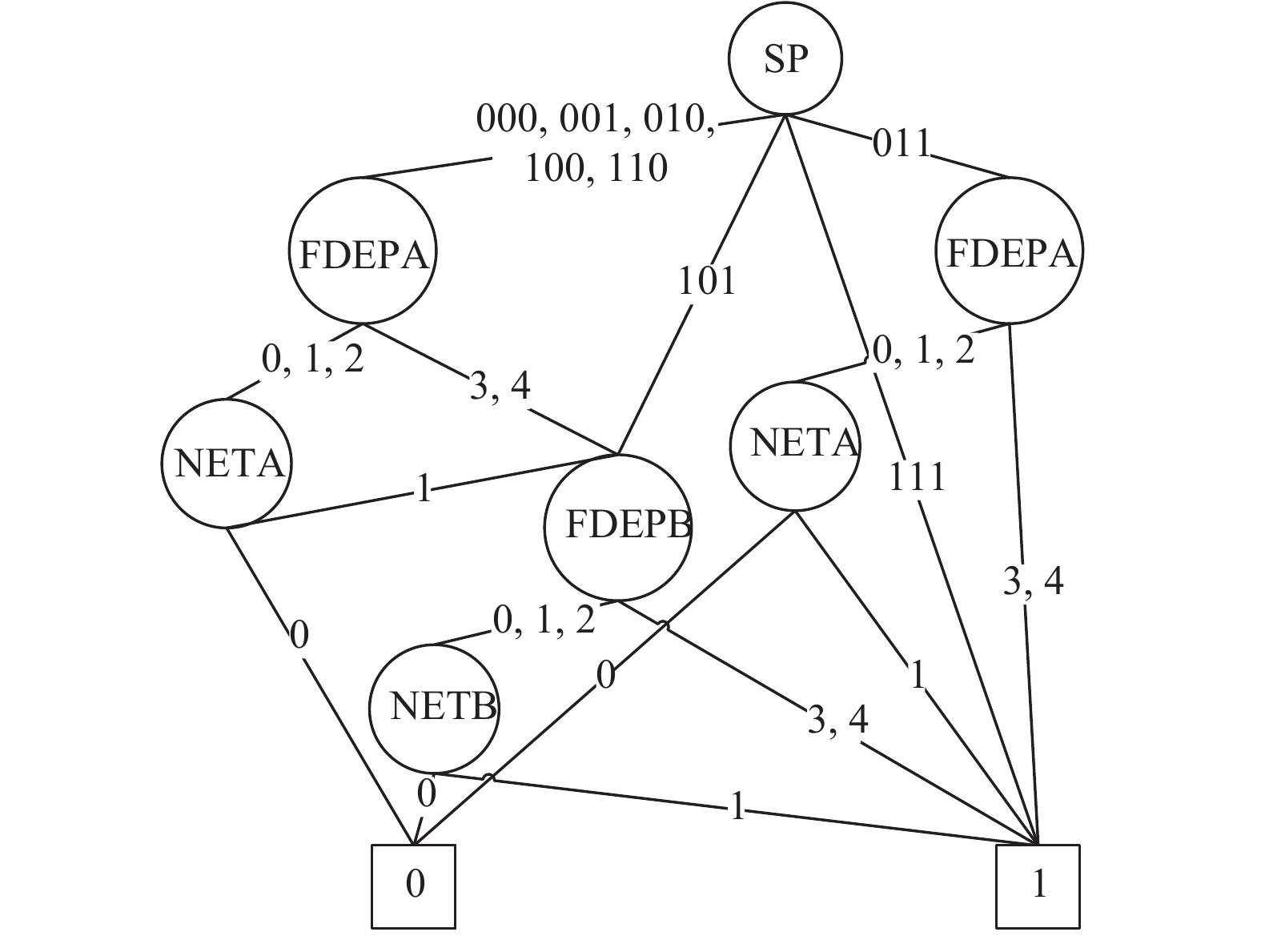
根据该系统的动态故障树DFT模型可以得到文献[10]中的系统性能初始MDD, 如图8所示.
|
图 8 高可靠性网络计算系统的初始MDD |
下面用文中给出的边值多值决策图的构造方法来获得其EVMDD. 将SP的4个分支分别用0到3的4个状态值代替. 即000,001,010,100,110用状态0代替; 101用状态1代替; 111用状态2代替;011用状态3代替.
图9所示的系统动态门的MDD, 按照本文所述的边值求解规则和缩减规则得到图10所示的EVBDD.
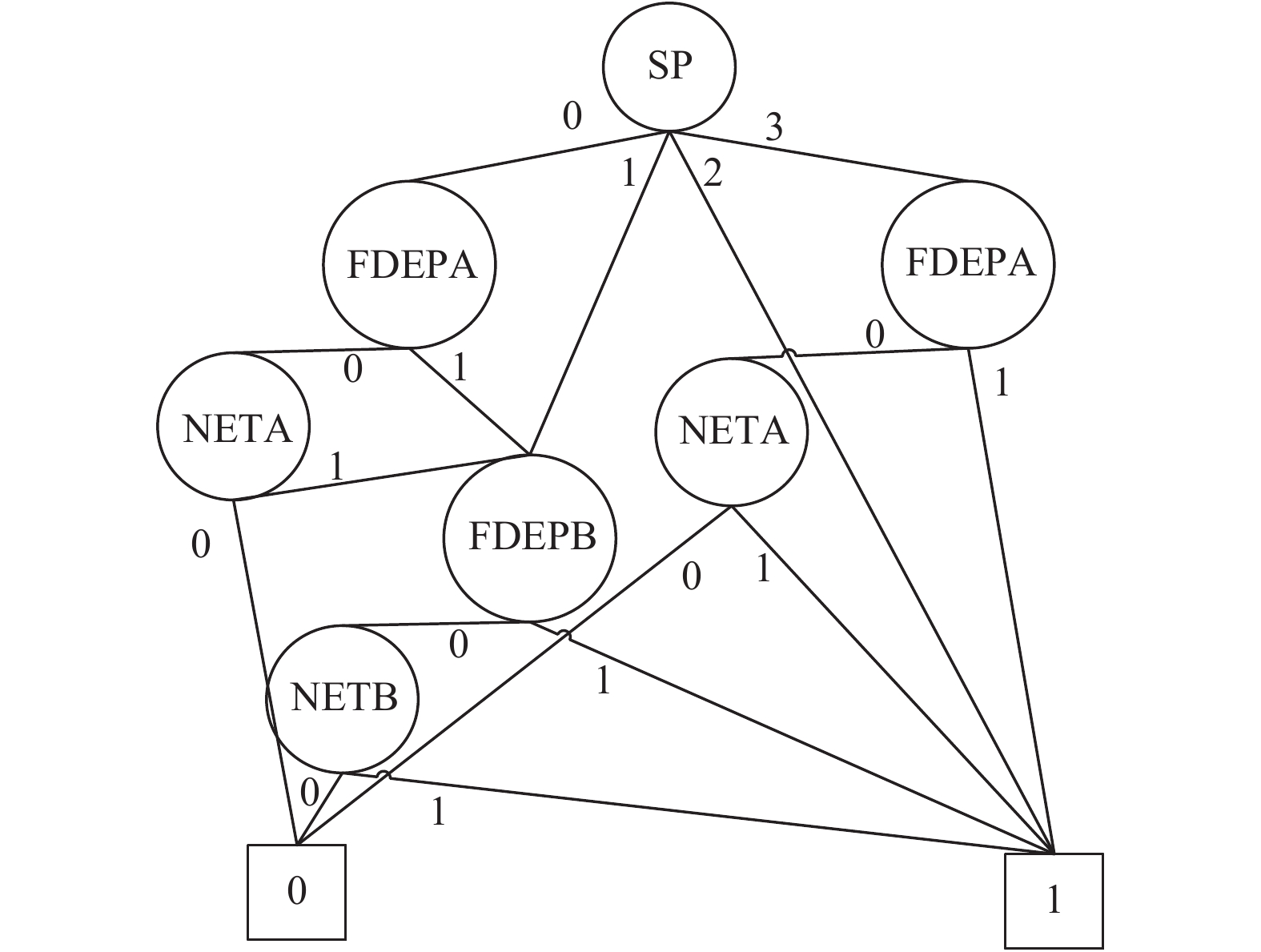
|
图 9 高可靠性网络计算系统动态门的MDD |
由于此系统比较简单, 所以EVMDD在节点和分支的数量上减少的优势没有显现. 但依据图6可见, 相对于MDD来说, EVMDD在节点和分支的数量上都有所减少, 系统越复杂, 边值多值决策图在节点数量上的优势越明显.
4.2 环境检测物联网络我国空气污染形势严峻, 部分城市面临雾霾、沙尘暴等环境问题. 环保部门积极开展大气污染治理, 其核心是对污染源的精准监测和对污染数据的精准分析. 随着物联网技术的发展, 多功能、智能化、小型化的微观站监测设备得到广泛使用. 研究环境检测物联网络故障树的边值多值决策图模型, 假设环境参数主要有温度、湿度和气体浓度, 分别用X2、X1、X0来表示, 设备的最终检测状态用f来表示, 每一个参数的测量都有一个备份电路. 因此用状态0表示完全无故障, 状态1表示部分故障, 状态2表示完全故障. 得到多值函数f的取值表如表3所示, 环境监测物联网络MDD如图11所示.

|
图 10 高可靠性网络计算系统动态门的EVMDD |
| 表 3 多值函数f的取值表 |
按照本文所述的边值求解规则和缩减规则得到如图12所示的环境检测物联网络的EVMDD.
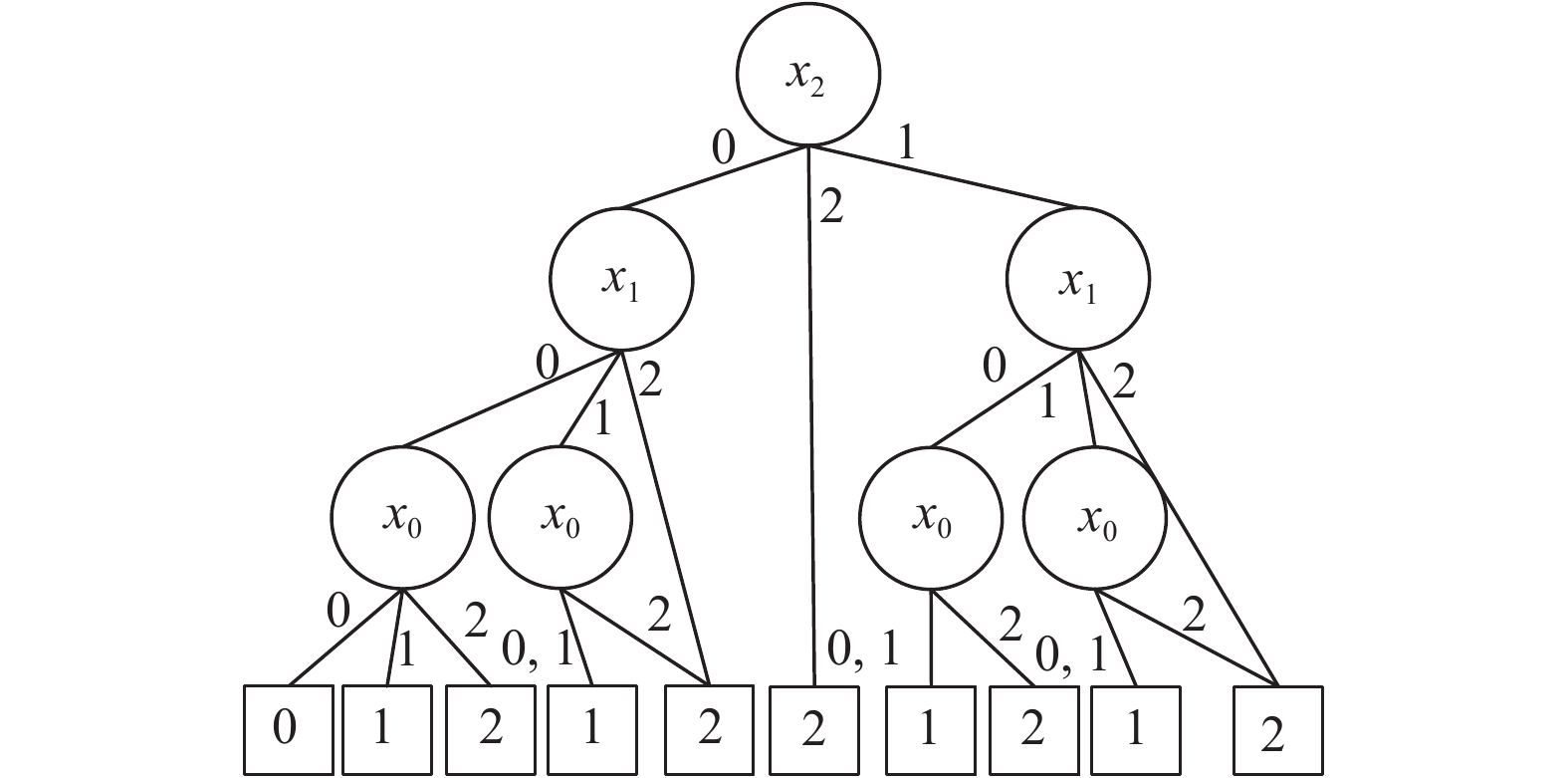
|
图 11 环境检测物联网络的MDD |
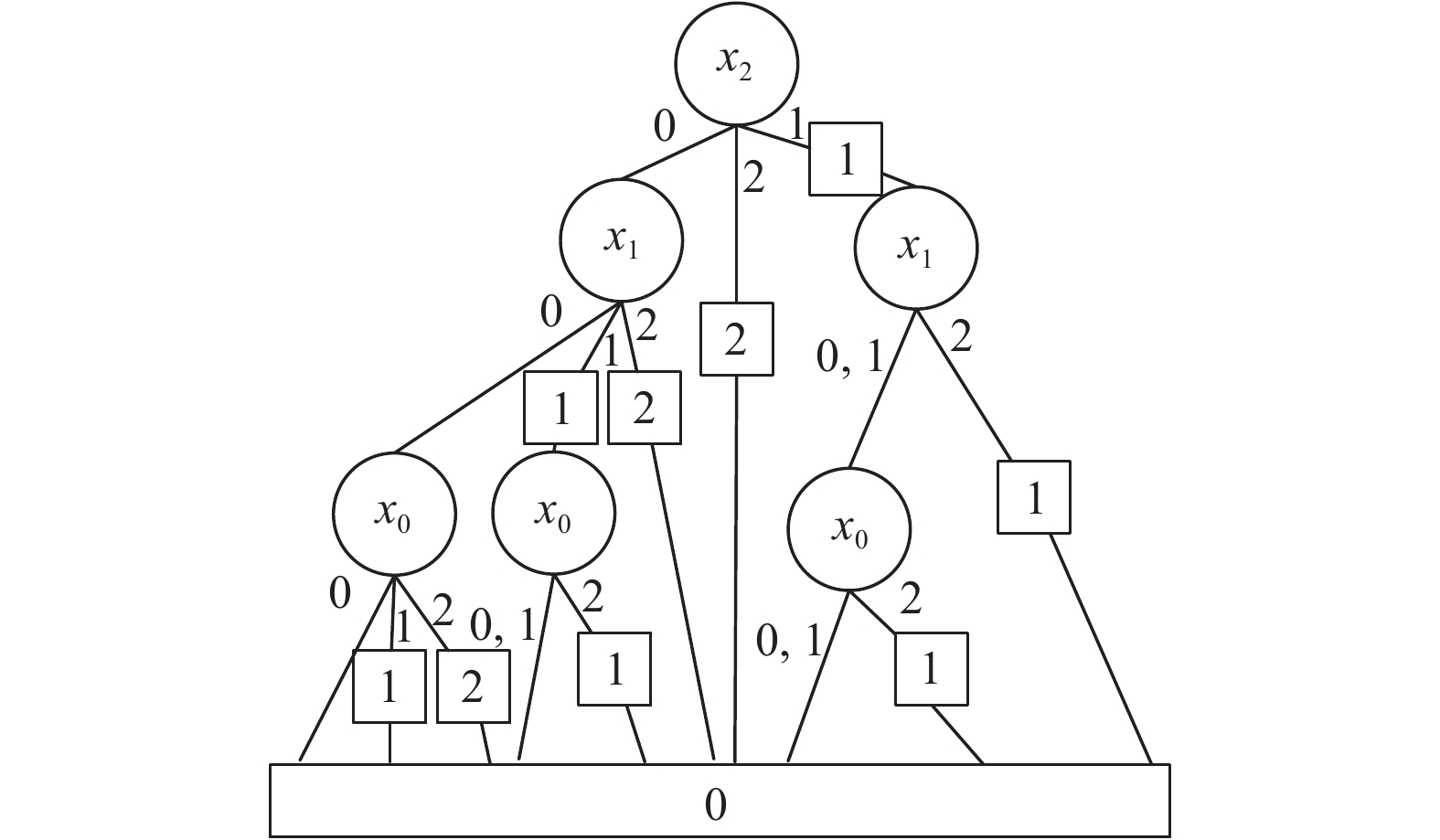
|
图 12 环境检测物联网络的EVMDD |
通过对环境检测物联网络的MDD和EVMDD的比较, 用EVMDD用更少的节点来表示环境检测物联网络. 而计算的时间复杂度与决策图中的节点数量成正比, 即节点数越少时间复杂度越低, 因此EVMDD在系统的故障树分析方面更有优势. 特别地, 随着状态数的变大, EVMDD的节点数远小于MDD的节点数. 我们预计系统将在未来变得更加复杂, 并且状态数将变得更大, 因此, EVMDD比MDD更有发展前景[15,16].
5 结束语本文对边值二叉决策图EVBDD和边值多值决策图EVMDD进行了系统的介绍和分析, 特别提出了边值多值决策图在动态故障树方面的应用. EVMDD可以更加紧凑的表示整个系统, 综合运用组合方法和状态空间方法, 这不仅使得状态空间爆炸问题得到缓解, 也使得计算速度得到提升, 可以广泛应用于现实生活中的多状态系统和多功能动态软件的性能分析等方面[17,18].
| [1] |
高顺川. 动态故障树分析方法及其实现[硕士学位论文]. 长沙: 国防科学技术大学, 2005.
|
| [2] |
段凌昊, 郭爱民, 潘勇. 动态故障树分析算法研究综述. 电子产品可靠性与环境试验, 2013, 31(4): 59-63. DOI:10.3969/j.issn.1672-5468.2013.04.014 |
| [3] |
Nagayama S, Sasao T, Butler JT. Analysis of multi-state systems with multi-state components using EVMDDs. Proceedings of the 42nd IEEE International Symposium on Multiple-Valued Logic. Victoria, BC, Canada. 2012. 122–127.
|
| [4] |
张红林, 付剑, 张春元, 等. 基于同构节点的动态故障树分析方法. 计算机工程与设计, 2011, 32(1): 1-4. |
| [5] |
古天龙. 一类新型抽象数据类型: 有序二叉决策图. 桂林电子科技大学学报, 2010, 30(5): 374-388. DOI:10.3969/j.issn.1673-808X.2010.05.002 |
| [6] |
凌牧, 袁海文, 马钊, 等. 改进的动态故障树转化为二元决策图的成分组合算法与应用. 系统工程与电子技术, 2016, 38(7): 1600-1605. |
| [7] |
高迎平, 李洋, 田楷. 基于有序二元决策图的动态故障树定性分析方法. 计算机与数字工程, 2016, 44(12): 2342-2347. DOI:10.3969/j.issn.1672-9722.2016.12.012 |
| [8] |
李佩昌, 袁宏杰, 兰杰, 等. 基于顺序二元决策图的动态故障树分析. 北京航空航天大学学报, 2017, 43(1): 167-175. |
| [9] |
钟艳如, 黄美发, 古天龙. 装配序列生成的有序二叉决策图技术研究. 计算机集成制造系统, 2008, 14(10): 1996-2004. |
| [10] |
张超. 基于BDD的动态故障树优化分析研究[硕士学位论文]. 西安: 西北工业大学, 2004.
|
| [11] |
Nagayama S, Sasao T. Complexities of graph-based representations for elementary functions. IEEE Transactions on Computers, 2009, 58(1): 106-119. DOI:10.1109/TC.2008.134 |
| [12] |
Doyle SA, Dugan JB. Dependability assessment using binary decision diagrams (BDDs. Proceedings of the 25th Inter-national Symposium on Fault-Tolerant Computing. Pasadena, CA, USA. 1995. 249–258.
|
| [13] |
Nagayama S, Sasao T. On the optimization of heterogeneous MDDs. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2005, 24(11): 1645-1659. DOI:10.1109/TCAD.2005.852290 |
| [14] |
王斌, 吴丹丹, 莫毓昌, 等. 基于多值决策图的动态故障树分析方法. 计算机科学, 2016, 43(10): 70-73, 92. DOI:10.11896/j.issn.1002-137X.2016.10.013 |
| [15] |
Nagayama S, Sasao T, Butler JT. A systematic design method for two-variable numeric function generators using multiple-valued decision diagrams. IEICE Transactions on Information and Systems, 2010, E93.D(8): 2059-2067. DOI:10.1587/transinf.E93.D.2059 |
| [16] |
王宁, 胡大伟. 基于多态多值决策图的多态故障树重要度计算方法. 计算机集成制造系统, 2015, 21(5): 1301-1308. |
| [17] |
季会媛, 孟亚, 孙权, 等. 一种容错系统可靠性分析方法. 计算机工程与科学, 2001, 23(5): 36-38, 50. DOI:10.3969/j.issn.1007-130X.2001.05.009 |
| [18] |
冯雪, 王喜富. 基于动态故障树的计算机联锁系统可靠性及性能分析研究. 铁道学报, 2011, 33(12): 78-82. DOI:10.3969/j.issn.1001-8360.2011.12.013 |
 2018, Vol. 27
2018, Vol. 27


