1 引言

随着计算科学技术的不断发展, 无线通信技术深度渗透, 越来越多实际应用需要知道物体的精确物理位置信息, 并因此产生各式各样的基于位置的服务, 由此定位问题受到了相当大的关注. 毫无疑问, GPS定位技术已基本满足了我们在室外场景中对于位置服务的多样化需求. 然而, 80%的人类活动行为是在室内进行的^[1]; 同时, 服务机器人、新型物联网终端设备等大量室内定位需求也发生在室内; 而室内场景受到各类障碍物的遮挡, GPS信号快速衰减, 定位能力严重受限制, 无法满足室内场景中导航定位的需要^[2].

其中, 射频识别(RFID)以非接触、非视距、低成本等优点, 成为热门技术. 尤其, 以倪明选、刘云浩等提出的非测距算法LANDMARC^[3]定位技术较为典型. 它通过引入参考标签, 统计分析目标标签、参考标签以及阅读器间的接收信号强度(RSS), 利用k近邻法估计坐标位置, 节约成本. 针对算法存在的问题, 文献[4]通过LANDMARC定位算法测得目标标签的理论坐标, 并利用三角测定法对N个已知参考标签重定位且获得理论坐标, 进而求出N个坐标位置得平均误差, 从而修正目标坐标, 但该误差修正无法准确反映实际目标的位置偏差, 定位精度较为有限; VIRE^[5]算法考虑到LANDMARC定位精度受参考标签密集度影响较大, 从而引入虚拟参考标签, 细化实际参考标签区域内网格, 把它当作实际参考标签使用, 参与k近邻法选择, 提高定位精度, 但是存在虚拟参考标签RSS值计算与实际偏差较大; 文献[6]提出了一种基于贝叶斯概率和LANDMARC相结合的室内定位算法, 利用高斯滤波器可以过滤一些异常的RSS值, 降低多径和环境干扰引起的位置波动和误差, 减少定位误差. 文献[7]提出了一种改进的三维LANDMARC室内定位算法, 引入数据融合算法和自适应算法, 提高LANDMARC算法的定位精度和适应性.

上述方法从不同角度去改进LANDMARC定位精度, 但存在近邻成员更新替代机制引起定位精度不高等问题. 本文提出了以最小关联度为准则, 通过计算该近邻区域的质心作为下一个参考标签依次迭代近邻成员, 直至与目标标签的关联度低于阈值, 从而估计目标标签的坐标, 实现预定位; 通过实施k近邻成员重定位并引入修正系数, 对预定位坐标进行偏差修正.

2 LANDMARC算法简介

LANDMARC算法的核心思想是通过利用引入参考标签替代部署阅读器, 借助阅读器对参考标签和目标标签的接收信号强度感知并对比. 原则上, 实际位置越接近目标标签的参考标签, 其在阅读器上的感知应该与目标标签更为相似. 故此, 找出它们之间的关联度, 并借助已知坐标的参考标签, 从而估计目标标签的坐标.

其算法通过计算, 对于每个目标标签均选取k个关联度值最小的参考标签作为k近邻成员. 其中, 关联度值计算采用它们信号强度的均方差来表示:

${E_{ij}} = \sqrt {\sum\limits_{p = 1}^M {{{({S_{ip}} - {\theta _{jp}})}^2}{\rm{ }}} } {\rm{ (}}i = 1,2,\cdots,U;j = 1,2,\cdots,N)$

(1)

其中, M、N和U分别是是阅读器、参考标签和目标标签的数目; E_ij表示第i个目标标签和第j个参考标签的关联度; S_ip表示第p个阅读器获得第i个目标标签的RSS值; θ_ip表示第p个阅读器获得第j个参考标签的RSS值. 由此可得, 关联度矩阵^[8]:

$E = \left[ {\begin{array}{*{20}{c}} {{E_{11}}}&{{E_{12}}}&{\cdots}&{{E_{1N}}} \\ {{E_{21}}}&{{E_{22}}}&{\cdots}&{{E_{2N}}} \\ {\cdots}&{\cdots}&{\cdots}&{\cdots} \\ {{E_{U1}}}&{{E_{U2}}}&{\cdots}&{{E_{UN}}} \end{array}} \right]$

(2)

显然, E_ij越小, 说明目标标签与参考标签的位置更接近. 由此, 对于每个目标标签, 从小至大选择k个E_ij值.

最后, 依据权重质心法^[9]和参考标签的已知坐标, 估计目标标签的位置:

$({x_i},{y_i}) = \sum\limits_{j = 1}^k {w(i,j)*({x_{ij}},{y_{ij}})} $

(3)

其中, E_ij表示第i个目标标签的第j个近邻的位置的权重, 其计算公式如下:

$w(i,j){\rm{ = }}\frac{{\frac{1}{{E_{ij}^2}}}}{{\sum\limits_{j = 1}^k {\frac{1}{{E_{ij}^2}}} }}{\rm{ }}$

(4)

表示离目标标签近的邻居参考标签的权重理论上要大于离待定位目标标签远的权重.

3 动态质心迭代与自偏差修正算法研究 3.1 动态质心迭代算法

尽管LANDMARC算法通过引入参考标签, 提高了目标标签的定位精度. 但k近邻成员的选择机制是静态的, 既当选取参考标签与目标标签之间关联度最接近的k个近邻参考标签后, 缺乏k近邻成员的动态迭代机制. 在k值确定的情况下, 若k近邻成员中存在与目标标签关联度较低的标签, 尽管通过弱化权重, 但是对目标标签位置估计的影响仍然存在, 这是不利的. 如果能够动态迭代k近邻成员, 将该关联度低的参考标签剔除, 引入关联度高的标签, 使得近邻成员逐渐逼近目标标签, 就可以克服这个不利影响. 因此, 本文提出了以最小关联度为准则, 即将当前估计质心纳入近邻成员, 并按从小到大对其关联度值进行排序, 剔除关联度最大的近邻成员, 从而实现动态质心迭代k近邻成员, 直至与目标标签的关联度低于设定阈值, 从而计算目标标签的坐标. 基本算法流程描述如下.

步骤1. 通过LANDMARC算法, 求出首批k近邻参考标签, k近邻参考标签与目标标签i的最小关联度矩阵 ${E_i} = \{ {E_{ij}}|i:\text{当前目标标签序号},j = 1,2,\cdots,k\} $ ;

步骤2. 已求关联度矩阵 ${E_i}$ , 并根据式(4)计算目标标签i当前k个近邻成员的权重, 即 ${w_i} = \{ {w\left( {i,j} \right)|i\text{代表当前目标标签序号},j = 1,2, \cdots ,k} \}$ ;

步骤3. 根据式(3)估计该近邻区域的质心位置 $C({x_c},{y_c})$ , 并可得到各阅读器在该位置的RSS值 ${S_{cp}}(p = 1,2,\cdots,M)$ ;

步骤4. 根据式(1)计算目标标签i与该估计质心位置的关联度 ${E'_{ic}}$ ;

步骤5. 设定阈值 $\delta $ . 若 ${E'_{ic}} \le \delta $ , 则该质心位置 $C({x_c},{y_c})$ 即作为该目标标签的最终估计坐标 $({x'_i},{y'_i})$ , 执行步骤6; 若 ${E'_{ic}} > \delta $ , 以最小关联度为准则, 将该估计质心 $({x_c},{y_c})$ 更新替代k近邻成员, 从而将原k近邻成员中关联度值最大的近邻成员剔除并更新E_i, 跳转至步骤2继续往下执行;

步骤6. 结束.

3.2 自偏差修正算法

通过计算目标标签近邻区域的加权质心, 以最小关联度为准则, 动态迭代更新其k近邻, 实现对目标标签的逼近, 但其比较依赖于准确的RSS值. 在实际环境中, 不可避免的存在电磁波的反射、折射、多径效应等现象. 这些因素会导致不同区域或不同标签位置的信号衰落程度不同, 因此阅读器感知到参考标签和目标标签的信号受到影响, 接收信号强度值RSS发生偏差. 而整个LANDMARC算法对于RSS值的依赖性高, 若RSS偏差较大将导致较大的目标标签定位误差. 为此, 应该适当的对估计位置进行偏差修正, 从而尽可能的降低其对定位结果的影响.

为了改进上述问题, 通过对已知真实位置的参考标签实施重定位, 并将其定位差值反馈并修正待定位的目标标签. 具体的工作描述如下.

步骤1. 通过上文提出的动态质心迭代算法估计目标标签i的坐标, 设为 $({x'_i},{y'_i})$ ;

步骤2. 对目标标签i的k个近邻成员作为待定位目标标, 已知真实坐标为 $({x_{il}},{y_{il}})$ , l=1,2,…,k; 并利用基于动态质心迭代的改进型LANDMARC算法实施重定位, 得到k个近邻成员的估计坐标 $({x'_{il}},{y'_{il}})$ ;

步骤3. 引入修正系数 ${\beta _i}({\beta _i}_x,{\beta _{iy}})$ 对目标标签i的定位坐标值进行补偿, 计算公式为:

${\rm{ }}\left\{ {\begin{array}{*{20}{c}} {{x_i} = (1 + {\beta _{ix}})*{{x'}_i}} \\ {{y_i} = (1 + {\beta _{iy}})*{{y'}_i}} \end{array}} \right.$

(5)

${\beta _i}x$ : x坐标的修正系数, 其值为式(9);

${\beta _{iy}}$ : y坐标的修正系数, 其值为式(10).

对于目标标签i的近邻区域内, 对k近邻成员的重定位, 据已知真实坐标 $({x_{il}},{y_{il}})$ 和估计坐标 $({x'_{il}},{y'_{il}})$ , 评估统计该区域内标签的误差量, 进行优化拟合, 得到该区域内的修正系数 ${\beta _i}({\beta _i}_x,{\beta _{iy}})$ . 同一区域内, 该修正系数能够较好的反映该区域内的偏差以便补偿. 对此, 我们以横坐标x为例:

${\rm{ }}{x_{il}} = (1 + {\beta _{ix}})*{x'_{il}}$

(6)

对于k近邻成员的坐标估计总均偏差可描述为:

${\varepsilon _i}^{\rm{2}}{\rm{ = }}\frac{{\sum\limits_{l = 1}^k {{\varepsilon _{il}}^2} }}{k} = \frac{{\sum\limits_{l = 1}^k {{{[{x_{il}} - (1 + {\beta _{ix}}){{x'}_{il}}]}^2}} }}{k}$

(7)

要使得总均偏差 ${\varepsilon _i}^{\rm{2}}$ 最小, 由上式可知, 要令 ${\varepsilon _i}^{\rm{2}}$ 取得极小值. 不妨假设:

$f({\beta _{ix}}) = {\varepsilon _i}^{\rm{2}} = \frac{{\sum\limits_{l = 1}^k {{{[{x_{il}} - (1 + {\beta _{ix}}){{x'}_{il}}]}^2}} }}{k}$

(8)

对 ${\beta _i}x$ 求导, 并令其值为0, 即 ${f'_{{\beta _{ix}}}} = 0$ . 整理可得:

${\beta _i}x{\rm{ = }}\frac{{\sum\limits_{l = 1}^k {({x_{il}} - {{x'}_{il}})} }}{{\sum\limits_{l = 1}^k {{{x'}_{il}}} }}$

(9)

同理可得:

${\beta _i}y{\rm{ = }}\frac{{\sum\limits_{l = 1}^k {({y_{il}} - {{y'}_{il}})} }}{{\sum\limits_{l = 1}^k {{{y'}_{il}}} }}$

(10)

3.3 算法流程图

在LANDMARC算法基础上, 通过引入动态质心迭代与自偏差修正算法相结合的算法提高定位准确性和可靠性. 其算法流程如图1所示. 首先, 通过设定门限阈值 $\delta $ , 据此循环评估估计质心坐标与目标标签的关联度, 实现了动态更新目标标签的k近邻成员, 使预定位坐标逐渐逼近目标标签, 克服了静态k近邻选择机制问题, 提高了定位精度和稳定性. 在此基础上, 计算环境修正系数 ${\beta _i}$ 并对预定位坐标进行偏差修正, 解决了预定位坐标受区域内环境因素影响而产生误差问题, 减少环境对定位结果的影响, 提高了定位准确性, 使算法更具良好的环境适应性和稳定性.

4 仿真实验与结果分析 4.1 仿真环境

为了更好地验证改进算法的性能, 使用Matlab R2014a对经典LANDMARC算法及本文提出的改进算法进行定位性能仿真实验. 本次仿真实验采用的信道传输模型是对数距离路径损耗模型, 路径损耗因子取值为2, 参考距离取值为0.1 m. 设定定位区域范围为8 m×8 m的空间^[10], 并将坐标(0,0)、(0,8)、(8,0)、(8,0)设置为阅读器所在位置. 同时, 在该区域内部均匀部署16个参考标签, 水平和垂直方向上相邻参考标签的间距均为2 m, 外层参考标签与区域边界的距离为1 m; 另外, 在该区域内设定了20个目标标签, 布局如图2所示. 并假设所有标签均在各阅读器的覆盖范围之内.

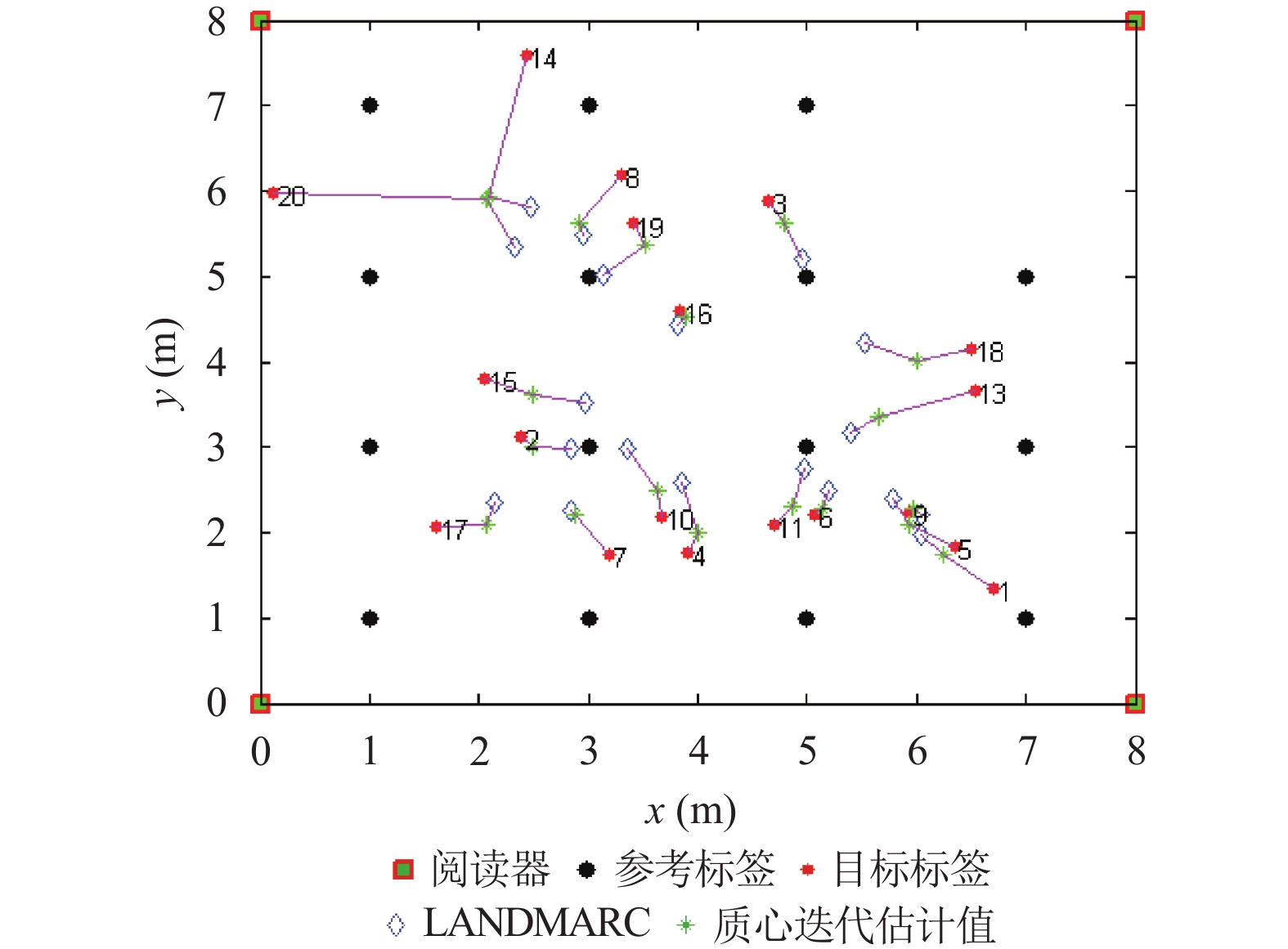
4.2 结果分析

设定近邻参考标签数k=4, 并于仿真环境中对LANDMARC算法及改进算法进行仿真. 定位结果如图3和图4所示. 图3为LANDMARC和质心迭代改进法定位结果比较; 图4为LANDMARC质心迭代及偏差修正法定位结果比较.

结果表明, 本文提出的动态质心迭代改进算法在定位精度上, 相比于LANDMARC, 整体上有明显提高. 换言之, 以最小关联度为准则, 通过计算该近邻区域的质心作为下一个参考标签依次迭代近邻成员, 直至与目标标签的关联度低于阈值的方法, 使得对目标标签的估计值越接近实际位置, 从而实现定位精度提高. 与此同时, 对于RSS固有偏差, 采取的基于参考标签重定位与引入区域修正因子的误差反馈相结合, 对目标标签定位进行校正, 进一步有效提高了定位精度, 效果更为明显. 但是, 在边界区域的定位精度尽管提高了, 但差距仍较为明显.

此外, 采用标准均方差误差(RMSE)^[11]对定位误差进行分析. RMSE是比较常见的定位精度评估标准, 其公式为: $e = \sqrt {{{(x - {x_0})}^2} + {{(y - {y_0})}^2}} $ . 图5为LANDMARC及改进算法各目标标签定位误差直方图.

由图5可知, 基于动态质心迭代的改进算法相比于LANDMARC, 在各个目标位置上均由较大提升. 而对质心迭代后的定位结果进行适当的误差修正, 定位精度定进一步得到提高, 误差较小, 更接近目标标签. 但在编号14、20上, 改进前后的误差仍较大, 发现这三个点处于较为边缘区域位置, 主要原因在于边缘区域为部署相应参考标签或提出针对的解决方法, 这也是下一步需改进的工作.

为了进一步比较LANDMARC和改进算法的性能, 表1列出了若干个目标标签的定位结果数据. 表2列出了几种算法的最大误差、平均误差.

表1和表2进一步验证了本文提出的基于质心迭代与偏差修正的方法有效的提高了定位精度, 平均误差为0.282 m. 当去除边缘目标标签后, 本文提出的算法的最大误差为0.488 m, 平均误差达0.153 m.

5 结论与展望

针对RFID环境下, 传统LANDMARC算法当k近邻成员选定后, 没有更新迭代逼近机制等问题, 从而影响了定位精度. 本文提出了以最小关联度为准则, 通过计算该近邻区域的质心作为下一个参考标签依次迭代近邻成员, 直至与目标标签的关联度低于阈值, 从而估计目标标签的坐标, 实现预定位; 通过实施k近邻成员重定位并引入修正系数, 对预定位坐标进行偏差修正. 通过Matlab 仿真结果表明, 基于动态质心迭代和偏差修正相结合的算法比LANDMARC具有更高的定位精度. 当然, 也存在着诸如边缘区域定位精度误差仍较大等问题, 这也是下一步需要改进的工作.