1 引言

我国属于矿山资源大国, 矿山排土场的安全问题尤为重要, 很多排土场存在着滑坡危险, 排土场的选址, 堆放方式, 管理方式可能都会引起滑坡事故. 随着传感器技术的发展, 各种类型的传感器被应用到了矿山排土场的安全监测当中, 传感器能保持不间断地采集排土场的相关参数, 这些相关参数对排土场的安全指标具有重大意义, 在一定程度上体现着排土场的安全状况, 传感器传输的实时数据代表排土场的相关特征指标, 当技术人员接收到异常数据时, 排土场滑坡或许已经产生了, 若提前预测出传感器下一时刻的数据, 在一定程度上可以减少排土场滑坡造成的财产损失和人员伤亡. 针对国内相关研究, 常用的排土场滑坡风险分析预测方法有工程类比、案例推理、可拓理论等, 栾婷婷等提出了可拓理论预警方法^[1], 根据可拓评价指标只是瞬时性地判断排土场是否有滑坡危险, 该方法没有考虑到历史数据对现有数据的影响, 在一定程度上或许会影响到预测的精度; 梁冰等提出了采用电磁信号发射及信号测距的边坡内部位移监测的方法^[2], 该方法能实时性地监测排土场内部位移量和排土场边坡的安全状况, 但是该设计只是局限于了解到当前排土场的安全状况, 并不能对排土场下一时刻的安全状况做出相应的判断; 易庆林等提出结合多个监测点对滑坡整体移动的贡献率通过小波分析的方法推导出综合位移方程的方法^[3], 该方法在判断滑坡风险性方面有一定的实用价值, 但是复杂的数学方程求解过程需要耗费一定的时间, 同时该综合位移方程的泛化能力方面比较弱; 张伟等提出主成分结合BP神经网络在坝顶位移监控的方法^[4], 该方法虽然避免了建立复杂的数学模型过程, 但是BP神经网络在拟合高度非线性函数时经常会陷入局部最优, 出现欠拟合和过拟合现象. 这些分析方法理论比较完善, 能基本确定一定时期内排土场的安全状况, 但是由于影响排土场滑坡稳定性的因素较多, 且大多数因素具有随机性、模糊性等特征, 各因素之间的关系非常复杂, 很难用准确的数学方程进行描述, 这些方法在准确性、及时性及智能性方面存在缺陷.

LSTM网络通过自身特殊的设计^[5], 极好地避免了常规循环神经网络训练过程中存在的梯度消失和梯度爆炸问题, 因此其能够被有效地被训练, 进而真正有效的利用相关历史序列信息^[6]. LSTM已经在语音识别, 视频标签分类^[7]、声音识别^[8]、自然语言处理^[9]等诸多前沿领域中得到广泛研究和应用, LSTM弥补了循环神经网络的梯度消失和梯度爆炸、长期记忆能力不足等问题, 使其能够有效地利用长距离的时间序列信息进行预测, 矿山排土场各个特性指标都具有时间序列的本质特征, 为通过运用LSTM网络用多种数据源来判断矿山排土场是否有滑坡的风险的想法应运而生.

矿山排土场灾害监测是一个动态的时间序列, 排土场的稳定性的过程是渐变的, 也就是说当前排土场的稳定性与历史的稳定性相互关联, 多个特征指标间存在着相互关联, 通过各特性指标间的相关性分析, 得出地表位移这一排土场物理指标与内部位移、土压力, 土壤含水率等相关性较大, 同时结合调研的相关文献, 本文提出长短时记忆网络模型(LSTM), 通过传感器接收的已有数据, 采用多特征指标来预测下一时刻的地表位移量具有重大意义. 首先采用灰色关联度算法, 分析地表位移与其它指标的关联度^[10], 根据关联度大小对多变量时间序列进行筛选, 进而降低数据规模和复杂度, 最后, 利用LSTM网络对多变量时间序列与地表位移之间的非线性关系进行动态时间建模, 构建地表位移预测模型, 通过LSTM网络建立的地表位移预测模型, 将已有数据预测贵州某矿山排土场的短时期位移量预测, 结果表明, 本文提出的方法通过多变量时间序列预测地表位移的效果较好^[11].

2 系统算法分析与设计 2.1 数据预处理

以贵州某矿山排土场的从2016年12月19日~2017年11月20日的数据为研究对象, 数据集中包含8个特性指标, 分别是地表位移(Mp), 土压力(Dm), 内部位移(Ep), 湿度(Hum), 降雨量(Rg), 土壤含水率(Smc), 孔隙水压力(St), 温度(Tpr). 每组数据按一定周期持续更新,如图1所示. 影响山体滑坡的因素有许多, 地表位移是表示着山体表面的移动距离, 土压力表示山体之间的相互作用力, 在一定程度上表示着山体之间的紧密程度; 土壤含水率, 孔隙水压力, 温度, 降雨量, 湿度都会直接或间接地影响到山体滑坡, 故将这些特性指标作为分析对象.

排土场的原始数据存在着众多的异常值和少部分的缺失值, 由于矿山排土场的滑坡需要严格地按照时间序列来预测, 若直接对异常值进行舍弃, 对预测结果会造成较大的影响, 针对异常值, 先对异常值进行空值处理, 将其视为缺失值, 然后通过拉格朗日插值法对所有空缺值进行插值填补^[12].

${y_i} = {a_0} + {a_1}{x_i} + {a_2}x_i^2 + \cdots + {a_{(n - 1)}}x_i^{(n - 1)}$

(1)

$L(x) = \sum\nolimits_{(i = 0)}^n {{y_i}{\rm{ }}\prod\nolimits_{j = 0,j \ne i}^{{n}} {\frac{{(x - {x_j})}}{{({x_i} - {x_j})}}} \;} $

(2)

公式(1)和(2)中 ${y_i}$ 表示的是已知过个 $n$ 点的 $n - 1$ 次多项式, $n$ 个点的坐标为 $({x_i},{y_j})$ , $L(x)$ 为 $x$ 缺失值点对应的近似值.

数据集中的每个特性指标间存在着量纲差异, 为了消除不同量纲间的影响, 需要对数据进行无量纲化处理, 无量纲化有多种方法, 本文采用归一化法对数据集中的所有特性指标进行标准化, $x = [{x_1},{x_2}, \cdots ,{x_n}]$ .

$\hat x = \frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}$

(3)

公式(3)中 $ {{x}_{\min }} $ , $ {{x}_{\max }} $ , $ \hat{x} $ 分别表示x中的最小值，最大值，去量纲化后的值.

2.2 主成分分析(Principal Component Analysis, PCA)

矿山排土场特性指标总共8种, 排土场滑坡风险评价受多种因素之间的相互影响, 通过主成分分析(PCA)确立所有特性指标的主成分, 通过主成分确立出作为影响矿山排土场滑坡的重要的特性指标, 通过对矿山排土场的数据样本进行主成分分析.

${\rm{X = }}\left( {\begin{array}{*{20}{c}} {{{{x}}_{11}}}&{{x_{12}}}& \cdots &{{x_{1m}}} \\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{x_{n1}}}&{{x_{n2}}}& \cdots &{{x_{nm}}} \end{array}} \right)$ , 其中 ${x_{ij}}$ 为第 $i$ 个样本的第 $j$ 个指标的测量值, 对 ${\rm X}$ 通过公式(3)得到标准化阵:

${\rm Z} =\left( {\begin{array}{*{20}{c}} {{z_{11}}}&{{z_{12}}}& \cdots &{{z_{1m}}} \\ {{z_{21}}}&{{z_{22}}}& \cdots &{{z_{2m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{z_{n1}}}&{{z_{n2}}}& \cdots &{{z_{nm}}} \end{array}} \right)$

(4)

对标准化阵 ${\rm Z}$ 求相关系数矩阵 ${\rm R} = {({r_{ij}})_{m \times m}}$ , 其中 ${r_{ij}}$ 反映指标 ${Z_i}$ 与 ${Z_j}$ 的相关系数, 相应的表达式为:

${r_{ij}} = \frac{{\operatorname{cov} ({{{Z}}_{{i}}},{Z_j})}}{{\sqrt {D({Z_i})} \sqrt {D({Z_j})} }}$

(5)

公式(5)中 $\operatorname{cov} ({Z_{{i}}},{Z_j})$ 为指标 ${Z_i}$ 与 ${Z_j}$ 的协方差, 解相关性系数矩阵 ${\rm R}$ 的特征方程 $|{\rm R} - \lambda {{\rm I}_m}| = 0$ , 其中, $\lambda = [{\lambda _1},{\lambda _2}, \cdots, {\lambda _n}]$ .

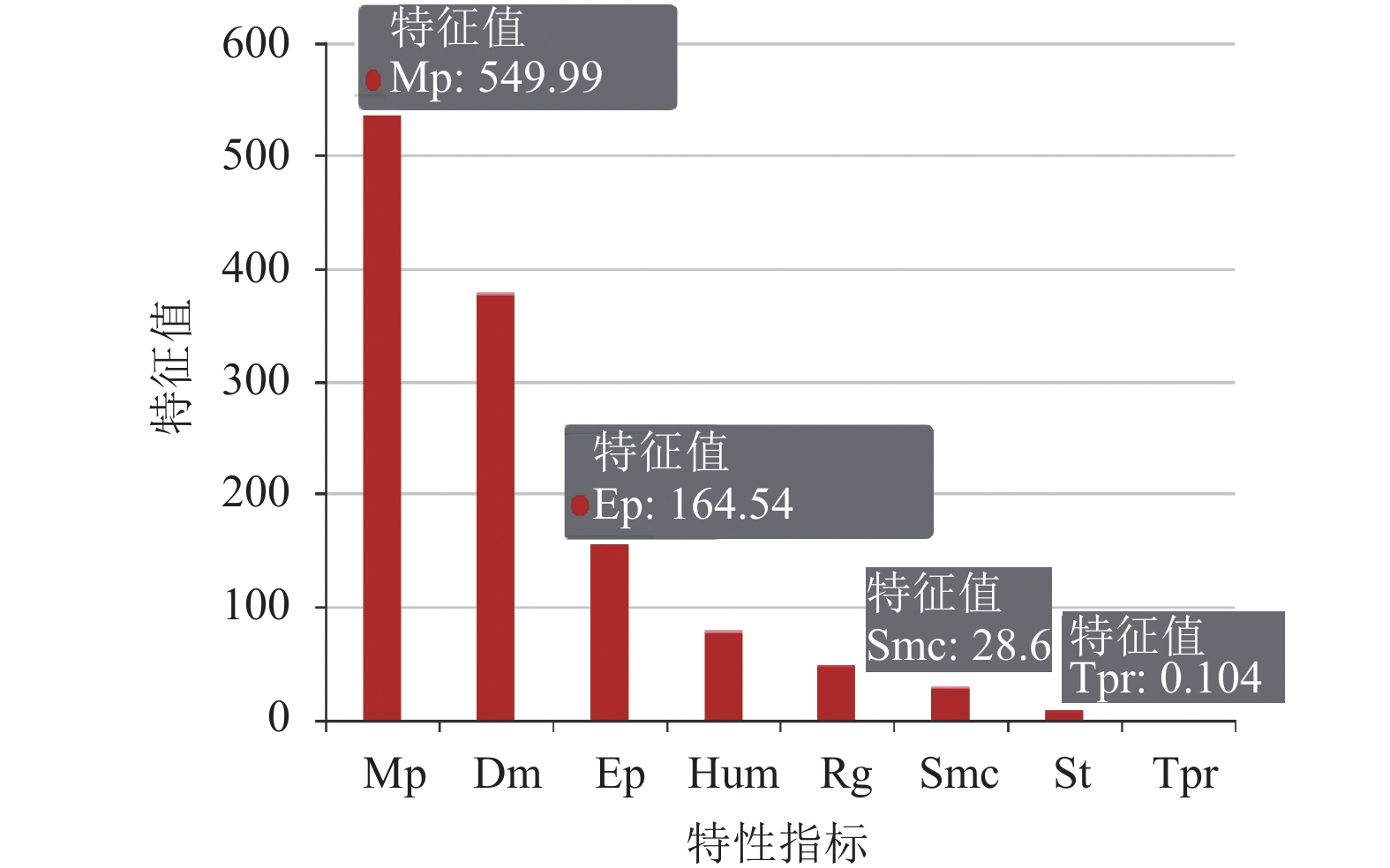
地表位移(Mp), 土压(Dm), 内部位移(Ep), 湿度(Hum), 降雨量(Rg), 土壤含水率(Smc), 孔隙水压力(St), 温度(Tpr)的特征值分别是549.99, 377.92, 64.54, 77.80, 48.50, 28.60, 8.28, 0.104如图2所示. 由各个指标的特征值, 地表位移特征值远大于其他指标的特征值, 由此, 在矿山排土场滑坡风险预测中, 地表位移可以作为重要的考虑对象.

2.3 各指标间的相关性分析

影响矿山排土场滑坡的因素有许多, 其中最明显的表征就是地表位移, 由2.2可知, 地表位移在所有特征值中为第一主成分, 因此可以将地表位移作为所有特性指标中对排土场滑坡影响最大的因素; 通过灰色关联算法求解地表位移与其它指标(内部位移、土压力、孔隙水压力、土壤含水率、降雨量, 温度、湿度)之间的关联度.

灰色关联分析法决策的思想是根据某个问题的实际情况确定出参考序列^[13]; 然后, 通过方案的序列曲线和几何形状与参考序列的曲线和几何形状的相似程度来判断其之间的关联程度; 曲线和几何形状越接近则说明其关联度越大, 方案越接近参考序列, 反之亦然. 设有 $n$ 个对象, 每个对象有 $m$ 项指标, 由于每个评价的指标量纲是不一样的, 为了消除量纲之间的差异对结果的影响, 需对评价指标数据进行归一化处理, 如(3)式, 归一化后的数据为 ${x_1},{x_2}, \cdots ,{x_n}$ . ${x_i} \!=\! [{x_i}(1),{x_i}(2), \cdots, {x_i}(n)]$ , 令地表位移为参考序列 ${x_0}$ , 则 ${x_0}$ 与 ${x_i}$ 关于第 $k$ 个指标的关联系数为:

${\xi _i}(k) = \frac{{\Delta \min + \rho \Delta \max }}{{{\Delta _i}(k) + \rho \Delta \max }}$

(6)

其中, $ i = 1,2, \cdots ,n;k = 1,2, \cdots ,m$ .

$\Delta \min = \mathop {\min }\limits_i [\mathop {\min }\limits_k (|{x_0}(k) - {x_i}(k)|)]$

$\Delta \max = \mathop {\max }\limits_i [\mathop {\max }\limits_k (|{x_0}(k) - {x_i}(k)|)]$

公式(6)中: $\rho $ 为分辨系数, 取值区间为[0, 1], 依据熵权法的特点, 排除主观因素的干扰, 在本文中将 $\rho =$ 0.69, 作为求解个特性指标间关联度的分别系数^[14]

第 $k$ 个指标与参考数列的关联度:

${\gamma _k} = \frac{1}{n}\sum\limits_{i = 1}^n {\xi (k)} $

(7)

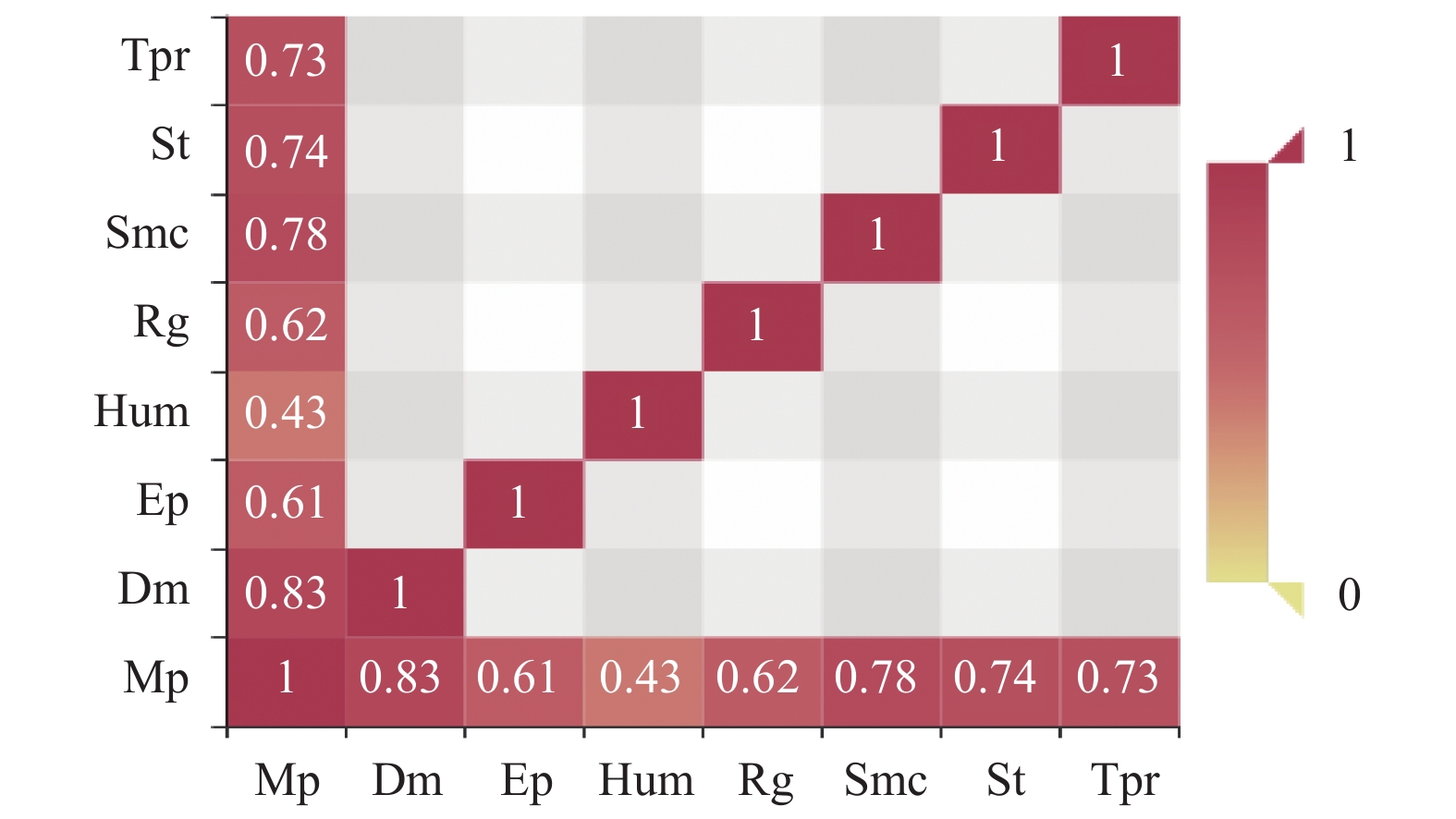
由公式(6)与公式(7)可得出其它排土场参数指标与地表位移的关联度, 地表位移(Mp)与土压力(Dm), 内部位移(Ep), 湿度(Hum), 降雨量(Rg), 土壤含水率(Smc), 孔隙水压力(St), 温度(Tpr)的关联度为0.8325, 0.6114, 0.4312, 0.6233, 0.7827, 0.7416, 0.7404如图3所示, 由关联度的大小可知土压力, 土压力, 土壤含水率, 温度这几个特性指标与地表位移的相关性较大, 其对地表位移综合影响为利用多变量同时预测地表位移下一时刻提供了可能.

3 长短时记忆网络模型(LSTM)进行多变量地表位移预测 3.1 LSTM网络模型的搭建

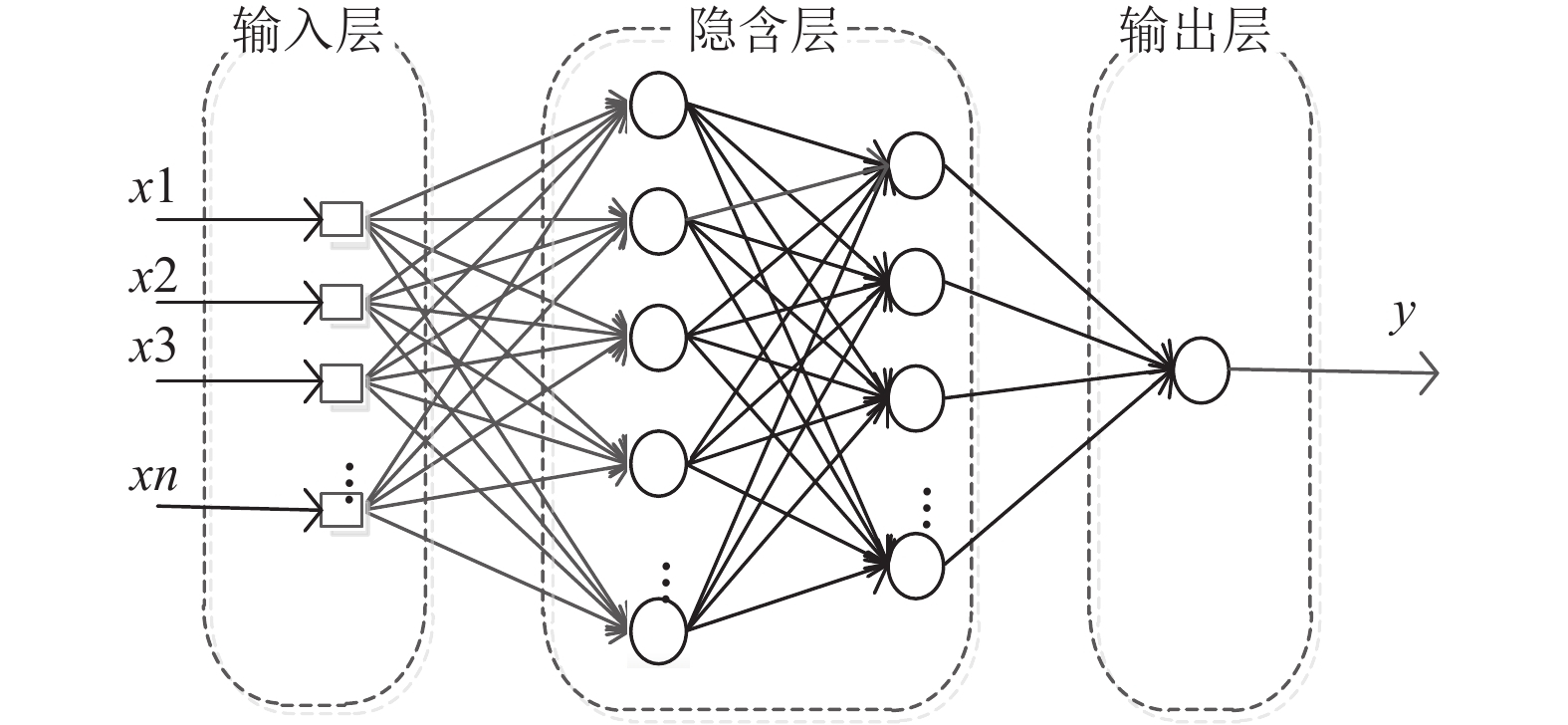
由2.2可知地表位移在所有特性指标中为第一主成分, 可以利用地表位移作为预测排土场滑坡的重要特性指标, 同时由2.3得出地表位移与其他特性指标间的关联度大小, 为利用多个其他特性指标预测地表位移提供了重要依据. 基于LSTM的多变量预测得的神经网络拓扑结构如图4所示.

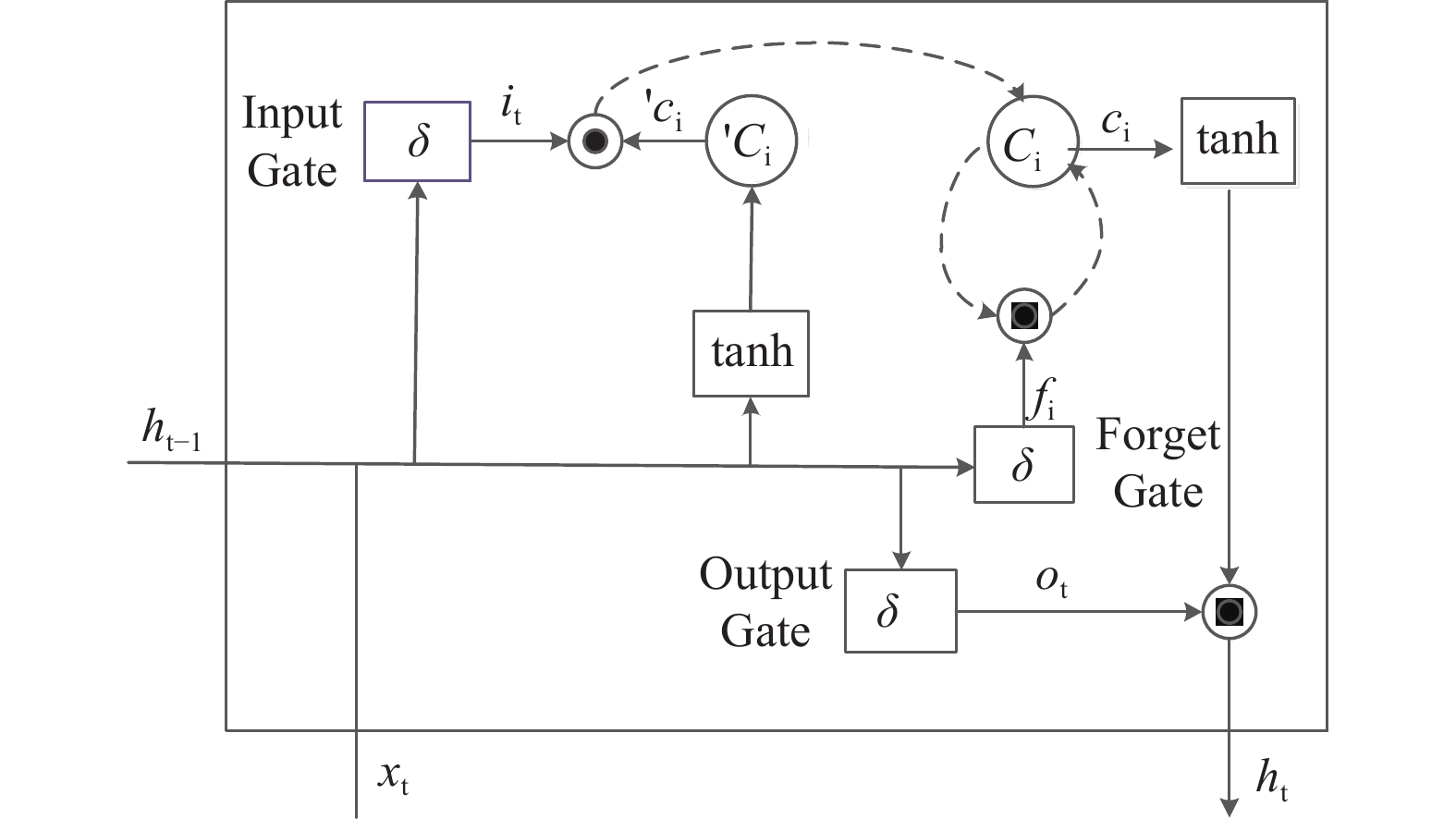
图4中, 输入层为经过有监督时间序列化处理后的矿山排土场的各特性指标, 隐含层为长短时记忆网络(LSTM), LSTM是RNN的一种变体, 是RNN的一种特殊单元, LSTM将RNN中隐含层的神经元替换成了记忆块, 每个记忆块中包含一个或多个记忆细胞和3种非线性求和单元, 这样的做法很好地解决了传统RNN存在梯度消失的问题^[15], LSTM存储单元的基本结构如图5所示; 输出层为下一时刻地表位移这一特性指标.

存储单元的运作原理由以下面5个公式表示:

${f_t} = \delta ({W_{xf}}{x_t} + {W_{ht}}{h_{t - 1}} + {b_f})$

(8)

${i_t} = \delta ({W_{xi}}{x_t} + {W_{ht}}{h_{t - 1}} + {b_i})$

(9)

${c_t} = {f_t} \cdot {c_{t - 1}} + {i_t} \cdot \tanh ({W_{xc}}{{\rm{x}}_t} + {W_{hc}}{h_{t - 1}} + {b_c})$

(10)

${o_t} = \delta ({W_{xo}}{x_t} + {W_{ho}}{h_{t - 1}} + {b_o})$

(11)

${h_t} = {o_t} \cdot \tanh ({c_t})$

(12)

上式中, $\delta $ 表示使用sigmoid函数对信息进行变换, ${C_t}$ 为存储状态, InputGate(输入门)用于确定需要更新的信息, ForgetGate(遗忘门)用语控制从存储状态丢弃或继续保存前一时刻的信息, 整个单元通过遗忘门和输入门更新存储状态 ${C_t}$ , OutPut(输出门)用于确定存储状态 ${C_t}$ 中用于输出信息, ${c_t}$ 表示状态 ${C_t}$ 的输出; ${h_t}$ 为t时刻存储单元的所有输出; ${W_{x*}}$ 表示与输入信息 $x$ 相关的各个门的权值, ${W_{h*}}$ 表示与前一时刻的输出 ${h_{t - 1}}$ 相关的各个门的权值, ${b_*}$ 对应各个门的偏置 ${f_t}$ , ${i_t}$ , ${o_t}$ 分别表示t时刻遗忘门, 输入门和输出门的计算方法. LSTM模型训练过程采用的是与经典的BP算法原理相似的BPTT算法, 分为四个步骤:

1) 按照前向计算方法公式(8)–(12)计算LSTM细胞的输出值;

2) 反向计算每个LSTM细胞的误差项, 包括按时间和网络层级两个反向传播方向;

3) 根据相应的误差项, 计算每个权重的梯度;

4) 应用基于梯度的优化算法更新权重.

3.2 梯度优化算法

梯度算法是求解最优化问题的一类重要方法. 算法选取目标函数的负梯度方向作为搜索方向, 并且常依据目标函数的梯度来确定搜索步长. 梯度优化算法有随机梯度下降(SGD), RMSProp, AdaGrad, Adam等, 以平均绝对误差(MAE)为目标损失函数, 图6和图7表示的是不同梯度优化算法在训练集和测试集上的损失函数曲线, 发现Adam优化算法表现比其他优化算法效果更好, 本文选用适应性动量估计算法(Adam), Adam是一种有效的基于梯度的随机优化算法, 该算法融合了AdaGrad和RMSProp算法的优势, 能够对不同参数计算适应性学习率并且占用比较少的存储资源. 试验结果表明Adam相比与其它的随机优化算法在实际应用中整体表现更优^[16].

3.3 地表位移预测算法流程与评价指标

基于上述的相关模型和算法, 其具体流程为:

1) 数据预处理, 包括异常值的舍弃, 缺失值的填补以及数据的筛选;

2) 将数据转化为有监督的时间序列, 便于对对下一时刻的数值进行相应的预测, 划分训练集和测试集, 训练集为数据集的80%, 测试集为20%;

3) 训练与评价模型, 利用前两步处理后的数据和Adam优化算法, 学习率为1.0, 神经元的节点数为50, 采用Relu激活函数, 训练基于LSTM的深度神经网络.

性能评价指标有均方根误差(RMSE), 一致性指数(IA), 本文以RMSE来评估网络的预测效果, 如公式(13), RMSE的值越小则预测效果越好.

$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {|{y_i} - {{\tilde y}_i}{|^2}} } $

(13)

式(13)中, ${y_i}$ , ${\tilde y_i}$ 分别代表实际值和预测值.

4 试验与结果分析

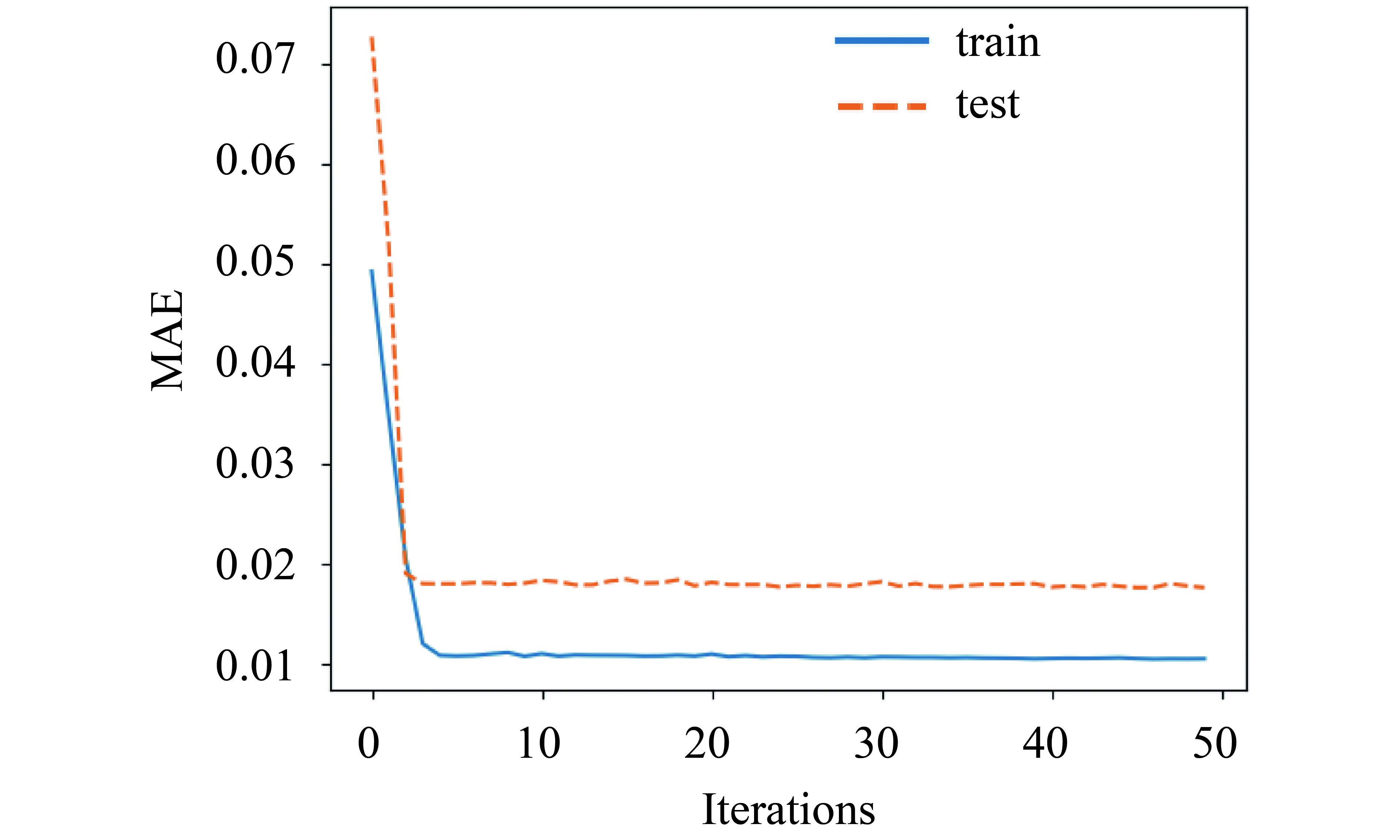
本文以贵州某矿山排土场的相关数据为验证对象, 根据主成分分析和关联性分析, 提出采用通过预测地表位移值的方法来判断矿山排土场滑坡的风险性. 根据地表位移与其它特性指标间的关联度大小, 选取地表位移(Mp)与土压力(Dm), 内部位移(Ep), 降雨量(Rg), 土壤含水率(Smc), 孔隙水压力(St), 温度(Tpr)这7个特性指标预测下一时刻地表位移的大小, 预测效果如图8所示, 图8中显示的是通过LSTM对地表位移预测的结果和真实值的结果, 从图中可以看出通过多变量预测地表位移的效果是比较好的, 通过多变量对地表位移的预测, 由于在前文对矿山排土场的数据分析当中, 得出地表位移在所有特性指标当中影响较大, 同时与其它特性指标间存在着较强的关联性, 对排土场地表位移的预测, 在一定程度上可以为矿山排土场的滑坡风险进行预估. 图9中显示的是在损失函数曲线的收敛状况, 从图中可以看出LSTM模型在进行数据训练和测试时效果都较好, 收敛速度块, 训练集和测试集的拟合效果较好, 均方根误差RMSE=1.7156.

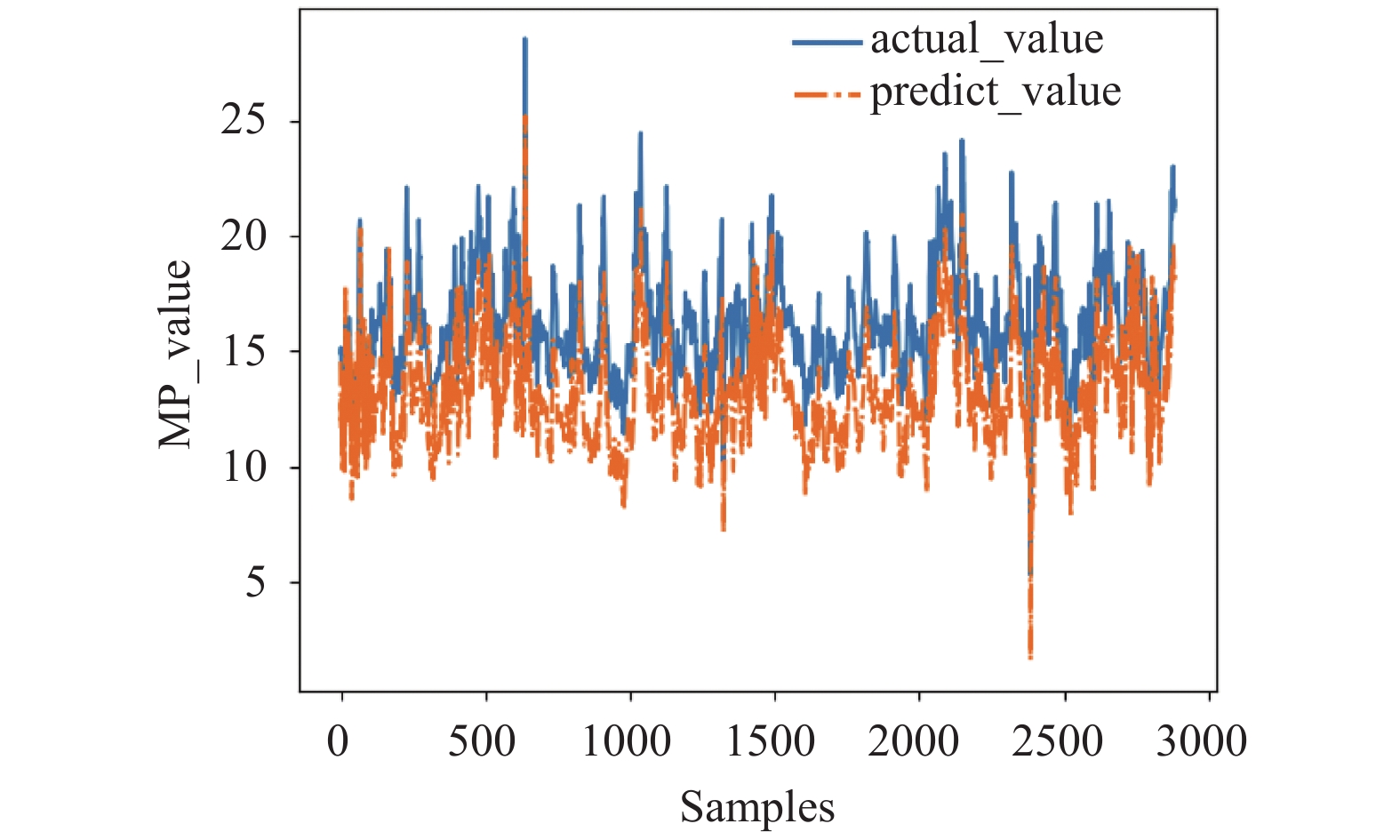
由2.3节可知, 地表位移与土压力(Dm)的关联度最大, 与湿度(Hum)的关联度最小, 为了验证各个特性指标对预测下一时刻地表位移的精度影响, 选取除土压力(Dm)特性指标以外的其它特性指标通过LSTM模型预测下一时刻地表位移. 预测效果如图10所示, 土压力(Dm)与地表位移(Ep)的关联度达到了0.8325, 在缺失土压力(Dm)这一指标特性指标的情况下, 地表位移的预测精度会大幅度下降; 在加上湿度(Hum)这一特性指标后, 通过LSTM的模型训练, 对地表位移预测的效果如图11所示, 其均方根误差RMSE=1.6932湿度(Hum)这一特性指标对地表位移的影响较小.

通过试验得知与待预测对象关联度较大的特性指标对预测结果的精度影响较大, 而与待测对象关联度较小的特性指标对与检测结果的精度影响很小, 本文提出的PCA-LSTM模型对矿山排土场下一时刻地表位移预测效果较好.

5 结论与展望

本文针对矿山排土场的滑坡发生的动态性、滞后性, 多组指标之间的高非线性, 影响矿山排土场滑坡的因素很多, 数据集中8个特性指标都会或多或少地影响排土场滑坡通过对所有特性指标进行数据分析, 在主成分分析当中地表位移为第一主成分, 同时由关联性分析得知地表位移与其它指标具有较大的关联性, 采用地表位移作为预测目标, 主成分分析与关联性分析结合有效减少了数据集的维度, 加快了预测效率, 主成分分析属于无监督学习算法, 在确定将地表位移作为预测目标时避免了人为选择的主观性.

本文提出采用以地表位移为显著特性指标对矿山排土场的滑坡风险进行预测, 通过LSTM模型的多个特征指标预测短时期内地表位移的状况, 进而提前预知排土场滑坡的可能性, 预测结果稳定性好, 为利用将多个特性指标综合成单个显著特性指标对矿山排土场滑坡预测提供了新的思路.