2. 中国林业科学研究院, 北京 100091
2. Chinese Academy of Forestry, Beijing 100091, China
连续压机生产线的普及使人造板生产快速发展, 但是末端的缺陷检测环节仍依靠人工检测, 存在工作强度大、检测正确率低等问题, 因此研发一套缺陷自动检测系统成为人造板行业的迫切需求. 连续压机连续工作, 板材之间的间距为400 mm, 运动速度高达1500 mm/s, 缺陷识别的实时性要求较高, 需寻求一种快速、准确的算法完成人造板在线缺陷识别[1]. 现阶段, 主要的缺陷识别算法有贝叶斯[2]、神经网络[3,4]、支持向量机(SVM)[5,6]、CART树[7,8]等, 取得了较好的成果. 由于贝叶斯分类方法需要计算出先验概率, 神经网络、支持向量机分类算法存在计算量大、复杂实时性不高, 均不适用人造板缺陷在线识别. CART树是一种基于二叉树的算法, 通过特征属性值不断对数据进行二分, 最终达到分类的结果[9]. 缺陷特征属性的选择决定了分类的成功与否[10], 根据人造板的特点提取形状、纹理特征用来表征缺陷. 由于CART树容易出现过拟合导致缺陷识别率较低的问题, 用代价复杂度的算法对生成的CART树进行剪枝, 使其具有更高的准确率. 本研究提出基于剪枝的CART树分类算法具有较高的实时性和正确率, 能够将其应用到人造板在线缺陷检测系统中, 促进缺陷检测的自动化发展.
1 最优CART树构建CART树采用自顶向下的递归方式, 在决策树的内部节点进行属性值的比较, 并根据不同的属性值判断从该节点向下的分支, 在决策树的叶节点得到分类结果[11]. 如图1所示, CART树由根节点、子节点、叶节点三个部分组成, 其中根节点和子节点代表特征属性, 叶节点代表类别.

|
图 1 CART树示意图 |
1.1 CART算法
构建CART树的算法流程如下[12]:
1)建立根节点N, CART树开始生长;
2)如果训练集L中只剩下一类样本, 则返回N为叶节点;
3)分别计算当前各个特征属性的Gini指数, 将得到最大的Gini指数特征属性作为节点, 使L划分为L1和L2两个子集, 之后递归构建决策树, 让其充分生长, 不剪枝.
Gini指数代表当前各个特征属性的分裂的程度, 数值越大说明数据复杂, 不确定性越大, 将Gini指数最小的特征属性设置为节点. 其中的Gini指数的计算如下:
假设训练集L中的样本有n个不同的类别Ci(i=1,…, n). 则概率分布的Gini指数定义为:
| $G(p) = 1 - \sum\limits_{k = 1}^n {\mathop p\nolimits_i^2 } $ | (1) |
式中, pi为类别Ci在S中所占比例. 训练集在某个特征属性V下被分为两部分L1和L2, 则L的 Gini指数即分裂指数为:
| $G(L) = G(L,V) = \frac{{\left| {{L_1}} \right|}}{{\left| L \right|}}G({L_1}) + \frac{{\left| {{L_2}} \right|}}{{\left| L \right|}}G({L_2})$ | (2) |
为了提高CART树分类器的泛化能力和降低复杂度, 本文采用基于代价复杂度的后剪枝的方法, 使用交叉验证的方式, 确保使人造板缺陷识别的相对误差与构建的决策树中节点数量均保持尽量小, 确定剪枝的阈值P, 进行剪枝. 因此, 在简化决策树, 可有效保持识别准确率. 具体实现过程如下.
1)剪枝后各个子树序列T构建
T是一棵是充分生长的CART树, 评估决策树的复杂度, 其代价复杂度函数为
| ${C_\beta }(T) = C(T) + \beta \left| {{N_T}} \right|$ | (3) |
式(3)中,
以节点为函数C为自变量, 则有公式(4):
| ${C_\beta }(t) = C(t) + \beta $ | (4) |
令β从0开始增加, 直到出现Cβ(t)=Cβ(T)成立的子节点, 得到剪之后的子树T2(T1为T), 不断增加β的取值, 重复上述过程, 最后只剩下一个根节点, 则得到一系列子树Tg(g=1, 2,…, n). 当式(3)与式(4)相等, 则P的值为:
| ${\beta _g} = \frac{{C(t) - C({T_t})}}{{\left| {{N_T}} \right| - 1}}$ | (5) |
式中, C(t)为子树Tt剪枝后节点t误分类损失, C(Tt)是未剪枝时子树Tt误分类损失.
2)最优DT构建
在子树Tg和 βg已知的情况下, 采用交叉验证方法评估子树的分类误差[13], 来确定最佳的剪枝阈值, 在确保正确率的同时, 降低CART树的复杂度. 误分类误差的定义为:
| ${E_{cv}}(T(\beta )) = \frac{1}{N}\sum {_{i,j}} d(i\left| j \right.){N_{ij}}$ | (6) |
式中, Ecv(T(β))为树T(β)交叉验证的误分类误差; d(i|j)为将j类误分为i类的样本数; N为训练样本数; Nij为误分类的样本数.
其交叉验证的过程为, 首先将训练集L划分为K个子集Ln(n=1, 2,…, K), 然后从L–Ln中生成K个子树Tn. 令
| ${E_{cv}}(T({\beta _g})) = \frac{1}{N}\sum {_{i,j}} {E_{cv}}({T_m}({\beta _g}'))$ | (7) |
经过循环交叉实验验证, 确定代价复杂度最小的子树Tk(β), 确定最小的相对误差结果是:
| ${E_{cv}}({T_k}(\beta )) = \min {E_{cv}}(T({\beta _g}))$ | (8) |
通过上述理论, 即利用L–Ln验证误差率、最后确定最佳剪枝阈值P(β), 最终得到误分类误叉最小的CART树分类模型.
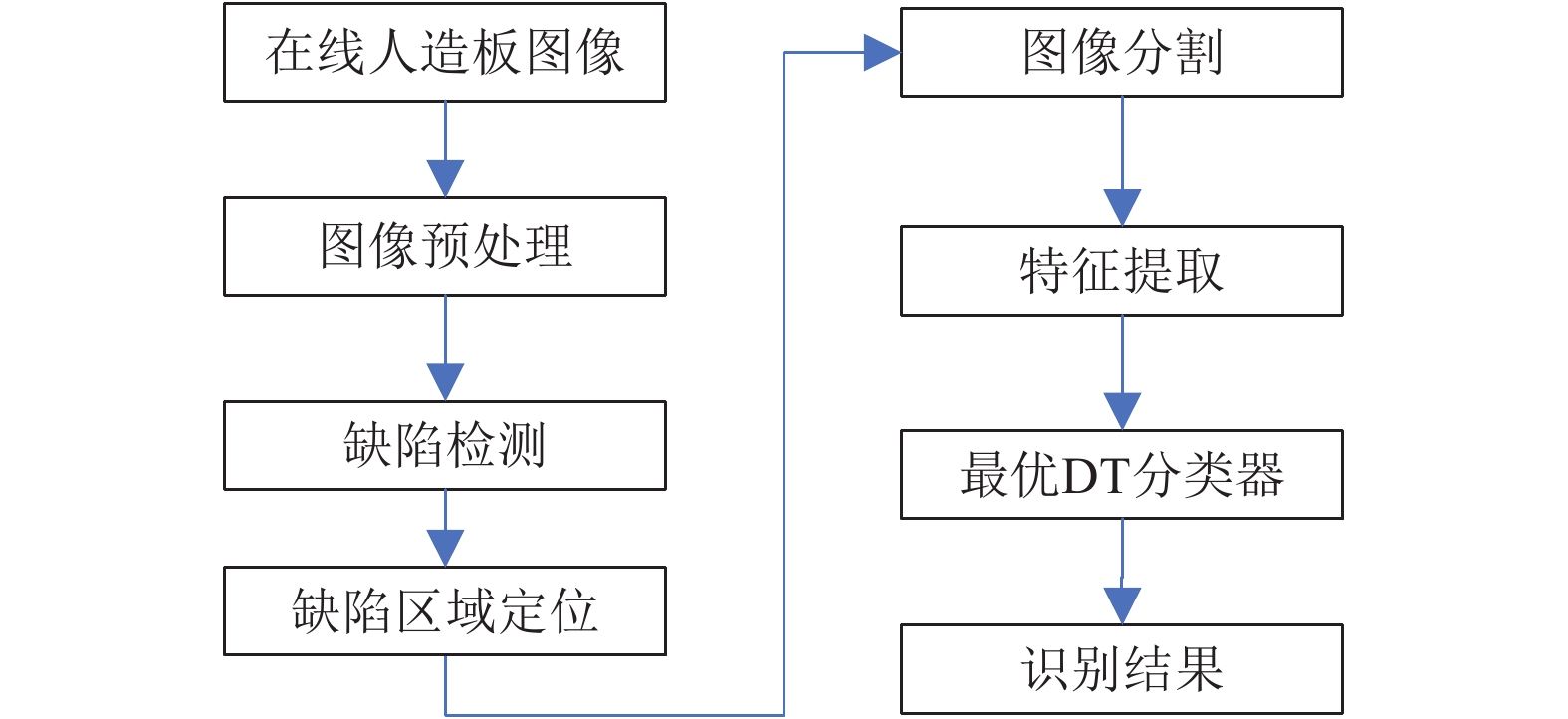
2 人造板缺陷自动识别人造板表面缺陷在线识别的实现流程如图2所示.
|
图 2 人造板缺陷自动识别流程 |
(1)图像预处理. 对CMOS相机获得的在线人造板图像, 用中值滤波去除噪声干扰.
(2)缺陷检测及区域定位. 将经过预处理的图像进行分块检测, 计算每一各区块的平均灰度值和方差, 将方差大于一定阈值定义为缺陷板, 并将该区块定义为缺陷区域.
(3)图像分割. 利用Otsu阈值分割法对缺陷区域进行分割.
(4)特征提取. 统计缺陷区域中的形状、纹理特征构成特征向量.
(5) CART树分类. 通过CART树分类器进行分类.
当有新输入的人造板图像时, 首先进行缺陷检测判断是否有缺陷, 如果检测有缺陷, 进行缺陷定位、通过图像分割、提取缺陷的特征值, 作为CART树的输入, 通过CART树得到缺陷类别. 其中最重要的是特征参数提取和最优决策树(DT)的构建.
2.1 特征提取人造板缺陷特征提取是缺陷识别的关键, 由于人造板图像的背景灰度值均匀, 缺陷区域内的灰度值相似, 各类缺陷的形状差异较大, 基于选取缺陷图像的形状、纹理特征对缺陷进行表征, 其表达式如表1、表2所示.
| 表 1 形状特征计算公式 |
| 表 2 纹理特征计算公式 |
表1中, N为缺陷区域内像素点的个数; Nb为缺陷区域边缘像素点的个数; MER为缺陷区域最小外接矩形; LMER为MER的长; WMER为MER的宽; SMER为MER的面积.
表2中, M(i)为缺陷各点的灰度值, N为缺陷区域像素点的个数.
2.2 人造板缺陷识别最优CART树的构建采用CART算法对大刨花、胶斑、杂物、油污四类缺陷的人造板图像进行训练, 从而获得缺陷自动识别CART. CART分类树的构建实质是建立人造板缺陷特征值与缺陷类别的非线性映射关系. 其输入向量为Q(S、L、O、OR、P、u、σD、σP、σS、σR), 输出为O(1, 2, 3, 4)分别代表大刨花、胶斑、杂物、油污, 建立映射关系为Q…O.
本文中用MATLAB软件进行程序编写, 首先提取220张人造板缺陷图像, 提取形状、纹理特征作为实验数据, 抽取其中200个数据构成训练集Li, 用于训练CART树, 剩下的20个数据组成训练集T, 用来验证CART树的优劣, 其实现过程如下所示:
1) 将200个人造板特征数据L分成10份即Li(i=1, 2,…, 10), 则训练集为L–Li为CART树的训练输入, 样本中的缺陷类别标签为训练输出, Li为测试数据用来确定剪枝阈值P;
2) 用CART算法训练出自由生长的决策树T;
3) 通过剪枝获得子树{T1, T2,…,Tn}, 其中T=T1, 利用Li测每棵子树的真实误差E(E1, E2, …,E10)的平均值, 将E中最小的值对应的阈值P为最优的剪枝阈值, 从而获得最优的CART树.
| 表 3 测试集混淆矩阵 |
2.3 人造板缺陷识别
当有新的人造板图像输入时, 首先对图像进行预处理, 通过检测区块的灰度均值和方差判断是否具有缺陷, 如果没有缺陷则不进行分割操作, 如果存在缺陷进行图像分割获得缺陷特征值, 将其作为CART树的输入, 通过CART树得到输出类别.
本研究的人造板图像是通过人造板生产厂家提供的, 共220幅. 通过对人造板缺陷图像其进行预处理、图像分割, 其分割后的图像如图3所示, 通过对图3中二值图像获得形状特征值, 将分割后的缺陷区域映射到原图中进而获得纹理特征, 从而获得表征缺陷的十个特征数据(S, L, O, OR, P, u, σD, σP, σS, σR).
3 实验结果及分析 3.1 最优人造板分类决策树构建在训练集L下根据CART算法训练出的未经过剪枝的CRAT树T如图4所示, 获得一系列子树及P(β1, β2, …, βk)值. 图4采用IF-THEN的形式表现出数据的分类过程. 当有新数据输入时, 根据根节点的特征属性与相应的数据进行大小判断数据的流向(此根节点属性为σP, IF x8>0.05592, 进入左子树), 进而逐渐的识别出人造板的四类缺陷, 之后确定剪枝阈值P, 进行剪枝操作.

|
图 3 四类缺陷分割前后图像 |
采用CART算法对训练数据L–Li得到的子树{T1 , T2,…, T10}, 通过由T得到的剪枝阈值
从图5可知, 随着P值增大(复杂度增加), 交叉验证相对误差逐渐增大. 图5中, P的值先为无穷大, 叶节点的数量代表树的复杂度, 剪枝过程从1~12开展, 共12次; 叶节点的数量从18变为8. 通过图4可以看出, 交叉验证误差在P的值为0.001开始增加, 所以最大剪枝次数为5, 此时交叉验证误差为0.05, 最终的叶节点数为8. 通过剪枝后, 决策树的叶节点树量减少, 树的复杂度明显降低, 最终剪枝后的最终结构如图6所示.
利用测试集的20组特征值数据对如图6所示构建的决策树进行检测, 其结果如表3所示, 其中行表示实际的缺陷类别, 列代表预测的缺陷类别. 从图中可知, 总的识别率达到95%, 可以满足人造板的识别正确率. 其中杂物和油污的识别率较低, 主要是这两种缺陷灰度值较为相似, 形状表现形式不一, 容易识别错误.
3.2 算法比较为了验证本研究提出剪枝的CART树分类算法的可行性, 与神经网络、支持向量机(SVM)以及未剪枝的CART树三种算法在人造板表面缺陷识别上正确率和时间进行比较.

|
图 4 充分生长的决策树 |

|
图 5 交叉验证结果 |

|
图 6 剪之后的决策树 |
3.2.1 正确率
利用测试集中的20组特征值数据对三种方法进行验证, 其结果如图7所示, 其中大刨花、胶斑、杂物、油污缺陷数量为2、5、7、6. 由图可知, 剪枝后决策树分类器的识别正确率较神经网络、SVM两种算法有很大的优势, 对于杂物、油污两种难以区分的缺陷仍有较高的识别效率. 剪枝后CART树较未剪枝的决策树识别能力强, 这是由于未剪枝决策树在训练的时候对训练样本数据进行充分表达, 泛化能力较弱, 由此可知剪枝后CART具有较强的泛化能力.

|
图 7 三种算法缺陷识别比较 |
3.2.2 算法耗时分析
在Intel Core I5-7500U 2.4 GHZ, 6 GB内存的硬件环境下和Windows10, MATLAB2016b的软件环境下, 对剪枝后的CART树分类算法、神经网络和SVM三种方法在获得的人造板缺陷数据上CPU运行时间进行分析. 其中图像分割、特征提取为相同程序, 耗时分别为320 ms、90 ms. 三种算法在训练集、测试集耗时如表4所示, 由表可知, 未剪枝的CART树在训练和测试耗时最短. 神经网络和SVM主要是由于计算复杂, 训练所需时间较长.
| 表 4 耗时分析 |
从表4可以看出, 神经网络、SVM两种算法时间很短, 但属于黑盒, 分类过程难以让人理解, 不易应用到实际中. 而决策树在分类过程是根据不同的特征属性的特征值大小对数据不断的进行二分, 容易理解且容易实现. 结合人造板缺陷识别正确率、识别时间和可实行性可知, 基于剪枝CART树的分类模型满足人造板在线检测实时性和正确率的要求.
4 应用和结论将本研究获得的剪枝后CART树得出的模糊规则(IF-THEN)编写入C++程序中, 嵌入到基于机器视觉的人造板在线缺陷检测系统中, 缺陷检测率高达98%, 缺陷识别正确率高达93%. 本研究证明了设计的基于剪枝CART树的分类方法在人造板检测系统中应用的可行性和优势, 填补了我国人造板行业缺陷检测的空白, 推动人造板行业缺陷检测自动化发展, 为以后开展各类相似的缺陷检测提供了一种可行的方式.
| [1] |
张国梁, 瞿国富, 侯晓鹏, 等. 连续平压机入口角度动态控制方法. 农业机械学报, 2015, 46(4): 372-378, 343. |
| [2] |
杜超, 王志海, 江晶晶, 等. 基于显露模式的数据流贝叶斯分类算法. 软件学报, 2017, 28(11): 2891-2904. DOI:10.13328/j.cnki.jos.005350 |
| [3] |
Mu HH, Zhang MM, Qi DW, et al. The application of RBF neural network in the wood defect detection. International Journal of Hybrid Information Technology, 2015, 8(2): 41-50. DOI:10.14257/ijhit |
| [4] |
梁浩, 曹军, 林雪, 等. 基于贝叶斯神经网络的近红外光谱实木地板表面缺陷检测. 光谱学与光谱分析, 2017, 37(7): 2041-2045. |
| [5] |
Tan M, Hu ZF, Wang BY, et al. Robust object recognition via weakly supervised metric and template learning. Neurocomputing, 2016, 181: 96-107. DOI:10.1016/j.neucom.2015.04.123 |
| [6] |
Fan MY, Wei L, He ZZ, et al. Defect inspection of solder bumps using the scanning acoustic microscopy and fuzzy SVM algorithm. Microelectronics Reliability, 2016, 65: 192-197. DOI:10.1016/j.microrel.2016.08.010 |
| [7] |
黄新波, 李文君子, 宋桐, 等. 采用遗传算法优化装袋分类回归树组合算法的变压器故障诊断. 高电压技术, 2016, 42(5): 1617-1623. |
| [8] |
常辉, 胡修林, 张蕴玉. 基于CART算法的卫星星座原始构型选择策略. 华中科技大学学报(自然科学版), 2011, 39(6): 1-5. |
| [9] |
张亮, 宁芊. CART决策树的两种改进及应用. 计算机工程与设计, 2015, 36(5): 1209-1213. |
| [10] |
Cui WC, Chen S, Yu TS, et al. Feature extraction of X-ray chest image based on KPCA. Proceedings of the 2nd International Conference on Computer Science and Network Technology. Changchun, China. 2013. 1263–1266.
|
| [11] |
杜春蕾, 张雪英, 李凤莲. 改进的CART算法在煤层底板突水预测中的应用. 工矿自动化, 2014, 40(12): 52-56. |
| [12] |
Mburu JW, Kingwara L, Ester M, et al. Use of classification and regression tree (CART), to identify hemoglobin A1C (HbA1C) cut-off thresholds predictive of poor tuberculosis treatment outcomes and associated risk factors. Journal of Clinical Tuberculosis and Other Mycobacterial Diseases, 2018, 11: 10-16. DOI:10.1016/j.jctube.2018.01.002 |
| [13] |
杨柳, 王钰. 泛化误差的各种交叉验证估计方法综述. 计算机应用研究, 2015, 32(5): 1287-1290, 1297. DOI:10.3969/j.issn.1001-3695.2015.05.002 |
 2018, Vol. 27
2018, Vol. 27



