2. 复旦大学 上海市数据科学重点实验室, 上海 200433
2. Shanghai Key Laboratory of Data Science, Fudan University, Shanghai 200433, China
随着信息化融入工业化进程, 越来越多的工业企业已经完成了自动化、信息化建设[1], 企业产业链的各个环节都涉及到信息技术的应用, 如生产监控、成品检测、产品销售等. 传感器、RFID等技术与ERP、MES等信息管理系统已经应用于制造企业生产经营管理中并积累大量的工业数据. 相比于互联网大数据, 工业大数据的数据类型更丰富、来源更多样性[2]. 海量的工业大数据蕴含了价值巨大的生产制造与质量信息, 这些信息能为企业带来丰厚收益[3].
本文选取轮胎行业制造大数据作为工业大数据研究背景, 通过整合轮胎企业各个生产环节的多源异构数据, 构建结构化质量分析数据集; 对质量分析数据集进行决策树或关联分析挖掘, 可以帮助轮胎企业发现产品制造过程中的质量异常及其影响因素, 不仅能够精确定位质量问题, 还能帮助企业改善工艺流程参数, 降低产品的不合格率, 从而实现企业质量与效益的提升. 传统的ADTree算法不适用于大数据量的数据挖掘, 本文改进了ADTree决策树算法, 提升了其性能, 使其适用于轮胎大数据质量分析.
2 相关研究随着大数据概念的火热, 国内外对工业大数据的研究也逐渐兴起. Yan等提出了工业大数据问题的一种框架, 并介绍了智能制造、工业大数据带来的挑战, 如可靠性与安全性[4]. 张洁等[5]提出了一种大数据驱动的"关联+预测+调控"决策模式, 帮助企业深层次地挖掘工业生产规律, 提供精准决策. 杨枝雨使用决策树算法对工业印花质量问题进行了分析, 改善了印花质量的稳定性[6]. 国内外的研究虽然较为系统的阐述了工业大数据的背景、意义及解决方案, 但结合具体行业或企业工业大数据进行详细分析挖掘的实例并不多, 其中一个重要原因是工业大数据必须从工业企业处获得, 即工业大数据领域里, 真实数据的获取是制约学者们开展研究的一个难题[7].
针对制造企业质量异常数据分析, 可以采用ADTree、FP-Growth[8]等算法. 本文选取的是ADTree算法, 在工业大数据应用场景下, 常规的ADTree算法在处理大数据方面稍显低效. Pfahringer等[9]提出了ADTree的构建优化方案, 主要将z值改进为Zpure, 作为一种剪裁技术, 但这种方法需要在大量迭代后才有效果, 并且实验中数据集最多只有50 000条左右, 效果还有提升的空间. 杨碧姗等[10]提出了一种快速可拓展的ADTree优化构建算法BICA (Bottom-up Induction for Constructing ADTree), 该算法设计了新的数据结构AVW-set, 这个集合大小不受数据集大小制约. 同时, 该算法提出了自底向上的归纳算法, 避免了一些冗余计算, 提升了评估效率. 但是, 算法中AVW-set的生成与合并算法时间复杂度较高, 完全可以进一步优化. 此外, 生成算法中还存在修改零权重值的问题. 本文在BICA算法的基础上, 主要针对以上两点进行了改进, 使算法更为完善. 在应用方面,由于ADTree算法只能针对二分类问题, 所以将ADTree结合实际应用的研究较少, Watcharapasorn等用ADTree算法对营养不良导致病人在手术中出现意外这一问题进行了分析[11]. 本文在改进ADTree算法的基础上, 将其应用于轮胎大数据质量分析, 实现算法与实际质量异常的影响因素分析问题相结合.
3 轮胎质量分析需求与数据集成 3.1 轮胎质量分析需求随着工业市场竞争的越来越激烈, 制造企业要想得到客户的认可, 高质量的产品是不可或缺的[12]. 在大数据时代, 如何利用工业大数据的挖掘技术, 从海量生产制造数据中寻找影响质量的因素, 实现产品质量的有效控制与改善, 从而提高产品质量已经成为急需解决的问题, 这使得质量数据分析成为工业大数据的重要应用需求, 需求包括:
(1)轮胎产品生产全过程的质量追溯;
(2)轮胎生产过程的质量合格率统计分析;
(3)轮胎质量异常的影响因素分析.
质量数据分析流程主要为数据获取、数据预处理、数据分析和分析整理步骤. 其中, 数据分析主要使用数据挖掘来进行, 采用多种算法进行分析可以确保分析的完整性, 起到互补的作用. 轮胎的质量分析可以采用关联分析的方法, 挖掘出轮胎生产环节中的特征指标(例如主机手、设备、批次、工艺参数等)与轮胎质量检测结果之间的显著关联关系, 实现对质量问题的追溯. 除了关联分析之外, 针对二分类问题(如轮胎质量检测分为合格和不合格两种), 可以使用决策树中的ADTree算法进行分析, 这也是本文采用的挖掘算法.
总的来说, 产品质量异常数据分析有两个难点:
(1)由于工业数据体量庞大, 使用传统SPSS、WEKA等分析工具效率较低, 一次处理数据量有限, 本文主要使用HDFS+ Hive+Spark作为工业大数据质量分析的技术支撑平台.
(2)传统的ADTree算法效率有限, 不太适合大数据分析, 本文优化了ADTree算法, 提高了其性能.
3.2 轮胎质量数据集成轮胎大数据涵盖了轮胎的整个生命周期, 种类较多, 轮胎企业非常看重其中的质量大数据. 轮胎在整个生产过程中重点是硫化与成型工序, 同时轮胎的动平衡检测是轮胎质量检测中的关键一环[13]. 与动平衡检测结果相关的数据包括轮胎的硫化数据、成型数据.轮胎质量异常数据集中所包含硫化机的温度、压力等属性均是一系列时序数据, 对这些属性进一步细化抽取其统计指标作为辅助性特征, 这些统计特征包括平均值、方差、最大值、最小值等. 对轮胎生产中的时序型数据分别计算上述统计指标, 添加到质量异常数据追溯分析数据集中作为后续分析的基础.
总体来说,轮胎质量数据可以分为两大类数据, 分别是质量检测数据和质量生产数据. 质量检测数据是产品生产完成后进行的检测数据集, 主要包括产品编号、各个检测项目和检测结果, 其中动平衡检测结果包括三个指标BAL_RANK, RO_RANK与UFM_RANK, 每个指标在1到5中取值, 只要三个指标中至少有一个指标为4或5, 则产品为不合格品. 质量生产数据是产品在生产过程中产生的相关数据, 主要包括产品编号、各设备编号、生产时间、班组、各操作人员, 各工序的工艺参数集等. 以上两种数据可以用产品标号关联起来, 形成结构化的质量数据集.
轮胎生产制造的各种数据存储在企业的MES、ERP等不同系统中, 这些数据需要整合起来. 首先使用数据接口将这些数据存储在关系型数据库中. 然后, 利用Sqoop配置关系型数据库与HDFS之间的数据连接[14], 以增量导入的方式获取所有质量相关数据, 构建大数据存储中心来实现数据集中管理. 接下来进行数据预处理工作, 如重复数据的去除、数据缺失处理等[15]. 最后, 使用多表合并技术, 在Hive中集成前面获取到的所有质量数据, 去建立结构化质量分析数据集, 该数据集将应用于数据挖掘的进一步分析[16].
4 基于ADTree决策树的质量分析 4.1 轮胎质量大数据分析方法图1展示了质量数据分析的流程, 其中数据获取和数据预处理已在3.2节阐述. 质量分析分为单因素分析与多因素分析. 单因素分析即使用统计的方式, 通过执行HiveQL查询语句, 得到单个因素与不合格率的关系. 对山东玲珑轮胎公司的千万级轮胎质量数据进行单因素分析, 可以得到一些初步结论, 例如不同物料编码的轮胎不合格率差异十分明显, 其中21种物料编码的轮胎占产品总数的0.7%, 却产生了13.3%的不合格品. 单因素分析同样能排除一些影响因素, 例如轮胎硫化班组分早、中、晚班, 容易想到晚班的工人是否会因为精力不济导致不合格率增加, 但是统计结果表明三个班组的平均不合格率几乎相同.
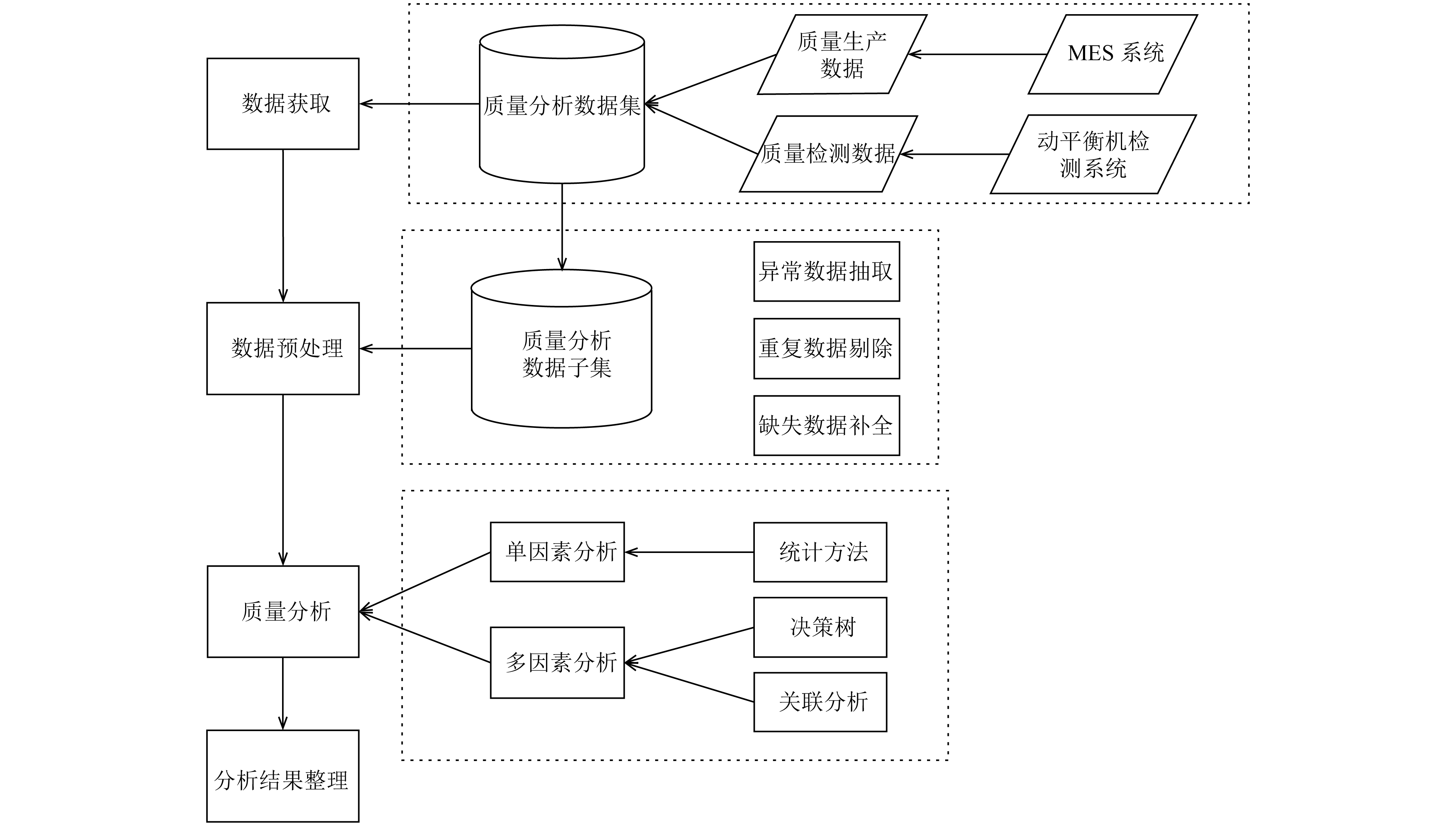
|
图 1 质量数据分析流程 |
产品质量的多因素分析使用数据挖掘的方法来找到造成不良品的影响因素. 本文将使用ADTree决策树作为轮胎质量分析的算法, 把轮胎生产过程中的硫化工序工艺参数特征值(内温、内压、模温、板温的最大值、最小值、平均值、方差)、硫化操作人员(CUR_ZJS_ID)、成型操作人员(ZJS_ID)、各生产设备(POT_ID, EQUIP_ID, EQUIP_CODE)、生产班次(CLASS)、生产车间(WOKR_SHOP_CODE)、生产模具(MOLD_ID)、生产批次(CUR_BATCH_ID)作为ADTree算法的输入, 并将qualified字段设为标记字段,该字段为1代表产品合格, 如果为2则代表产品不合格. ADTree算法将输出一个决策树作为挖掘结果. 由于传统的ADTree算法效率较低, 无法进行大数据下的分析, 因此本文将对ADTree算法进行改进.
4.2 传统ADTree算法ADTree算法由Freund和Mason提出[17], 其优点在于, 它的分类准确率往往比其他决策树算法要高, 可以同时处理离散型和数值连续型输入参数, 并且能够给出预测结果的置信度. ADTree不仅能做分类工作, 其个别节点还可以评估自己的预测能力, 因此在轮胎质量分析问题中, 可以通过节点来分析导致最终质量不合格的潜在影响因素.
ADTree算法适用于解决二分类问题, 例如轮胎质量分析中的合格与不合格就是典型的二分类情况. ADTree的图形显示和传统决策树不同, 它包括两种节点: 预测节点和决策节点. 决策节点对应一个分裂测试, 训练集的样本经过分裂测试后被划分到相应预测节点中. 每个预测节点p对应一个预测值, 同时包括一部分样本, 划分到某个预测节点的样本集称为F(p).
传统ADTree算法的输入包括两个集合, 第一个集合里的每一个元素包括了属性向量和分类值, 其中分类值的取值为1或–1(也可以为1或0), 在轮胎质量分析中分别代表不合格与合格. 第二个集合是权重Wi(样本i的权重)的集合. ADTree的构建需要经过T次迭代, 每次迭代找到全局的最佳分裂测试, 然后生成相应的预测节点和决策节点. 最佳分裂测试通过(1)式取到最小值来获得:
| $z = 2\left( {\sqrt {{W_ + }\left( c \right){W_ - }\left( c \right)} + \sqrt {{W_ + }\left( {\neg c} \right){W_ - }\left( {\neg c} \right)} } \right) + W\left( {\neg p} \right)$ | (1) |
其中, c代表分裂测试, W+(c)即预测节点样本中满足c的正标记权重和, W(¬p)为不在预测节点里的样本权重和.
4.3 ADTree改进算法传统的ADTree算法受限于性能, 不适用于大数据问题. 学者Pfahringer提出了一个新的公式:
| ${Z_{\rm{pure}}} = 2\left( {\sqrt {{W_ + }} + \sqrt {{W_ - }} } \right) + W\left( {\neg p} \right)$ | (2) |
Zpure的计算不需要经过分裂测试, 只要累加F(p)的正负权重和即可. z和Zpure经过拉普拉斯修正后, Zpure会成为z的下限. 如果根据F(p)计算出来的Zpure已经大于等于当前迭代的最小z值, 那么当前F(p)的所有分裂测试评估值z都会大于等于当前迭代的最小z值, 所以这个节点不需要寻找更好的分裂测试, 可以直接跳过. 这种优化能提高传统ADTree算法的性能, 但效果有限. 杨碧姗等提出了BICA算法, 通过以空间换时间的策略, 降低了计算评估值z的复杂程度, 极大地提升了算法的性能. 本文在BICA算法的基础上做了进一步优化, 并修正了原算法中出现的零权重值问题, 提出了ADTree改进算法.
BICA算法定义了新的数据结构AVW-set(以下简称为set), set由ADTree算法需要处理的样本集生成. 表1是一个简单的样本集, 共有三条记录, 其中类别和权重是两个样本标识, 类别为1代表不合格, 类别为–1代表合格, 而权重一般初始都设为1. 除去样本的标识, 每个样本有两个属性, 分别是操作人员和内温最小值. 样本的每个属性对应一个set, 如本例中就有两个set, 分别是操作人员的set和内温最小值的set. 每个set有三个属性, 分别是属性名、正标记权重和与负标记权重和. 如果set记录的属性attr是连续型的,取所有属性值v, 记录F(p)中满足属性attr≤v的正标记权重和与负标记权重和; 如果attr是离散型的, 只记录F(p)中满足属性attr=v的正标记权重和与负标记权重和.
| 表 1 预测节点p拥有的样本集 |
以表1的样本集为例, 内温最小值属性是连续型的. 第一个值是95.5, 在三个样本中只有一个样本的内温最小值小于等于该值, 同时该样本的类别为1, 故取其权重1, 算在正标记权重和里. 同理,第三个值是160.5, 三个样本的内温最小值都小于等于该值, 统计这三个样本的权重, 得到正标记权重和为1, 负标记权重和为2. 构建结果如表2所示.
| 表 2 内温最小值的set |
而操作人员属于离散型值, 且只有两种值. 20080001有两个样本, 所以负标记权重和为2. 操作手的set构建结果如表3所示.
| 表 3 操作人员的set |
BICA算法中的set在离散型属性的正标记权重和或负标记权重和为0时, 会赋一个自定义的较小值, 这是错误的. Pfahringer在其论文[9]的第3节提到了权重和为0不会影响ADTree算法的结果, 从解释性来说, 主机手20080001操作了两个产品, 都是合格的, 如果正标记权重和不设为0, 那么这个主机手的合格率就不是100%了, 这明显也不合理. 正确的做法是保留0这个值.
此外, BICA算法构建连续型属性的set时, 采用先扫描样本集, 获得所有属性值, 然后对属性值排序, 再记录每个属性值的正负权重和的方式. 假设样本数量是X, 不同属性个数是Y, 那么时间复杂度是O(X)+O(YlgY)+O(XY). 本算法在获取样本集所有属性值的同时, 直接记录每个属性值的权重和. 待属性值排序完毕后, 从小到大扫描一遍, 将权重和逐次累加即可, 前两步的时间复杂度不变, 第三步的时间复杂度从O(XY)降到了O(Y), 从而减少构建set的时间.
所有属性的set都建立完成后, 将被统一放到AVW-group (以下简称group)里作为一个集合.
在分裂测试中, 如果属性attr为连续型, 每个分裂测试为attr≤(Vj+Vj+1)/2, 即每两个相邻数值的均值. 如果属性attr为离散型, 分裂测试较为简单, 直接是attr=Vj. 这样设计后, set起到的作用就是记录了预测节点P的每个分裂测试c的正负标记权重和. ADTree中的内部预测节点的set可以根据下文介绍的自底向上的合并方法获得, 而传统ADTree算法在每个预测节点计算z时都要计算这两个值, 效率较低. 同时, set的定义确保了该数据结构的大小和样本数量无关, 只和每个属性的不同取值个数有关. 这样, 在计算Zpure时, 只需要扫描set的各个值即可, 不需要像传统ADTree算法一样扫描整个样本集. 设计set不仅减少了正负标记权重和的重复计算, 其容量一般也远小于样本数量, 所以set占的空间并不大.
BICA算法的分裂测试评估改为自底向上的归纳来进行, 可以省去部分内节点的group计算. 每个预测节点都有对应的group, 这涉及到group的合并问题.只要预测节点是ADTree的非叶子节点, 则取它的第一个决策子节点, 将其两个后代节点的group合并成本节点的group. 由于每个group包含多个set, 所以合并时根据同属性的set进行合并.
对于离散型属性的set, 直接合并相同属性的正负权重和即可. 对连续型set合并, 设合并后的set为P,待合并的set为X, Y, 其中X, Y在构建时已经排序. 整个过程通过归并排序的算法持续进行, x, y, p分别初始化为X, Y, P的末尾记录.
算法1. 连续型set合并
输入: 待合并set X, Y
输出: 合并后的set P
当x, y没有全部指向set起始记录时:
1) P[p].W+=X[x].W++Y[y].W+
2) P[p].W-=X[x].W–+Y[y].W–
3) IF X[x].value<Y[y].value
y=y–1;
4) Else if X[x].value>Y[y].value
x=x–1;
5) Else
x=x–1, y=y–1;
同时, BICA对连续型属性进行合并时, 会先扫描一遍两个待合并的set, 得到新set里的属性值, 再扫描一遍两个待合并的set, 计算出新set里的正负权重和.实际上, 只需要对两个待合并的set从后往前扫描一遍, 就可以生成新的set, 如上文的算法所示, 这样能减少合并的时间. 通过set的合并, 可以充分利用已知信息, 不需要重复计算, 同时合并的时间复杂度是线性的. 而传统的ADTree算法在评估z值时, 需要对每个预测节点的样本的每个连续型属性进行排序, 在大数据量情况下开销巨大.
本文对BICA算法中的ADTree构建算法进行了适当改进. 当算法遍历到叶子节点时, 如果叶子节点的正负标记权重和不全为正数, 那说明这个节点是完美分裂测试所生成的, 不需要再做处理. 原算法中缺少这一判断, 所以遍历到叶子节点后一定会进入算法的第4步, 这会增加算法的时间. 修改后的算法共T次迭代(即生成T个分裂测试), 每次迭代用后序遍历预测节点的方式, 通过得到最小的z找到最佳分裂测试, 生成新的预测节点p. 算法不仅采用了Pfahringer等提出的Zpure剪裁技术, 也结合了BICA自底向上归纳评估的思想, 分裂测试评估过程核心部分伪代码如算法2.
算法2. ADTree评估算法
输入: 根节点r及根节点的F(p)
输出: 节点的group
1) 访问一个预测节点p
2) 如果p是叶子
a) 根据F(p)计算group
b) 计算p的正负权重和、Zpure, 如果正负权重和不全为正数, 直接返回
3) 否则(即p是内节点)
a) 取p的第一个决策子节点d, d是p的决策子节点中的最佳分裂
b) 取d的两个预测子节点q与r, 计算它们的group, 然后分别作为输入, 递归调用本算法,这样就起到了后序遍历的作用
c) 将q与r的group合并为p的group, 计算p的正负权重和、Zpure
4) 如果当前p的Zpure小于当前最小的z, 因为Zpure是z的下限, 那么可能存在z比当前最小的z还小, 所以对于group里的所有set的所有值v
a) 计算分裂测试c的z
b) 如果z比最小的z还小, 那么最小的z设为这个值, 并且将分裂测试c设为最佳测试, p设为最佳分裂节点
5) 对于p除了第一个决策子节点d的其余子节点d (如果存在的话)
a) 取d的两个子节点q与r, 计算它们的group,然后分别作为输入, 递归调用本算法
5 质量分析结果与算法性能实验 5.1 质量分析结果本文对山东玲珑轮胎公司提供的千万级轮胎数据进行质量分析. 本例选取的轮胎物料代码是221003794, 可用样本数为308 880, 其中质检合格306 471, 不合格2409, 不合格率约为0.78%. 借助生成迭代次数为10的ADTree图形进行分析, 如下图所示,每一个椭圆形的节点是分裂测试, 每个分裂测试有两个矩形的子节点, 节点上的数字代表置信打分, 本例中这个打分较高的话则代表该因素可能对质量不合格有重要影响.
根据ADTree的挖掘结果, 使用Hive数据库对质量数据进行追溯, 查询ADTree挖掘出的质量影响因素对产品不合格率的提升程度, 可以得到如下结论:
1) 成型主机手20070488负责的产品中, 合格17 952件, 不合格1260件, 不合格率高达约6.6%. 这名主机手经手了约6.2%的产品, 却产生了约52%的不合格品, 可见其操作水平非常之低.
2) 其余主机手生产的轮胎, 在平均内压<1.776时,合格29 053件, 不合格413件, 不合格率约1.4%; 平均内压在[1.776, 1.817]时, 合格238 090件, 不合格731件,不合格率仅为约0.3%; 当平均内压>1.817时, 合格21 376件, 不合格仅5件, 不合格率几乎忽略不计. 由此可见, 轮胎硫化过程的硫化机平均内压对于最后的质检合格与否起到了重要影响.
3、硫化批次是20161206时, 合格864件, 不合格401件, 不合格率高达31.7%. 其中, 经手成型主机手20070488的951件产品更是有382件不合格, 不合格率约为40.1%; 剩余314件产品有20件不合格, 不合格率约为6.4%, 也远高于平均不合格率. 因此, 该批次的生产出现了明显的问题.
以上挖掘结果反映出几个问题. 首先是成型主机手20070488, 这名主机手的生产操作水平差得离谱, 严重影响了轮胎质量, 企业可以考虑对其进行技能培训, 或者调离岗位. 其次是轮胎加工中的平均内压, ADTree反映该工艺参数对轮胎质量有较大影响, 企业需要对照自身制定的工艺参数, 确保轮胎生产时平均内压处于合理范围内. 最后, 硫化批次是20161206 (即2016年12月6日)时, 平均不合格率非常高, 企业需要排查当天的生产状况, 分析可能存在的问题.
由于不同轮胎物料代码经过的设备、操作人员、生产工艺参数等均不相同, 因此每种轮胎物料代码的挖掘结果存在差异. 但通过整理, 可以总结出影响轮胎质量的普遍规律:
1) 操作人员的水平好坏会影响轮胎质量, 个别操作人员经手的轮胎不合格率会非常高, 企业应该及时采取人员改进措施.
2) 轮胎生产过程中的平均内压对轮胎质量有明显影响, 一般来说, 如果平均内压偏低, 那么轮胎的整体不合格率会有提升. 因此, 企业需要提高生产技术, 确保硫化过程的平均内压在合理范围内.
3) 由于少量生产设备存在问题, 导致该设备生产的轮胎品种不合格率偏高. 企业应该及时维修设备或考虑购置新设备, 以此保证产品质量.

|
图 2 ADTree算法挖掘结果图 |
5.2 算法性能实验
虽然现在已经有了较为成熟的大数据处理技术,但是算法本身的提升仍然会对整体性能有所提高. 以轮胎质量分析数据集物料编码221005405、221003790作为实验的数据集, 数据集大小为379 010. 实验环境为Intel i5 7000, 操作系统为Centos 6.8, 4台24 GB内存, 通过Java调用Spark并连接Hive进行实现. 实验比较结果见表4所示.
| 表 4 新算法实验结果比较 |
由实验可见, BICA算法相比于Pfahringer等提出的传统算法, 在建树时间上大大缩短了, 这是因为BICA用了set和自底向上的评估思路, 通过合并group这种利用已知数据的方法, 减少了Zpure和z的计算量, 节省了排序次数; 在排序方面, Pfahringer的算法在评估连续型属性时需要对整个数据集排序, 而BICA算法只对set中的属性值排序, 这也是性能提升的一方面. 本算法改进了BICA算法建立set, 合并group的方式, 优化了时间复杂度, 并且对树的构建算法也做了适当改进, 在其基础上进一步提升了性能.
内存方面, 由于算法的整体思路是以空间换时间, 因此传统的ADTree算法内存占用较低, 但新算法的内存占用并不大, 是可以接受的.
6 总结随着信息行业的快速发展, 很多工业企业正在大力建设工业信息化, 同时也积累了大量的工业数据. 在大数据时代的背景下, 如何利用这些数据成为了关键问题[18]. 通过分析、挖掘这些工业数据, 能够得到许多对企业有价值的信息, 使企业更好地发展.
本文选取轮胎行业大数据作为工业大数据研究的案例, 分析了轮胎行业大数据的需求与数据特征, 并开展了轮胎质量数据分析工作. 先利用大数据技术, 将轮胎生产各个环节的多源异构数据整合起来, 经过预处理等流程, 构建出大规模的结构化质量分析数据集. 本文重点介绍了使用改进后的ADTree算法进行轮胎质量多因素分析, 实验证明, 改进后的算法更适用于大数据背景下的数据挖掘. ADTree的挖掘结果经过整理, 可以找出影响轮胎质量的重要因素, 这种精确定位出来的问题能够帮助企业改善工业流程, 降低产品的不合格率, 从而实现企业效益的提升.
| [1] |
杨海成. 企业信息化建设与工业化进程融合的认识与思考. 中国机电工业, 2008(7): 80. |
| [2] |
李敏波, 王海鹏, 陈松奎, 等. 工业大数据分析技术与轮胎销售数据预测. 计算机工程与应用, 2017, 53(11): 100-109. DOI:10.3778/j.issn.1002-8331.1609-0154 |
| [3] |
宁宣凤, 吴涵. 浅析大数据时代下数据对竞争的影响. 汕头大学学报(人文社会科学版), 2017, 33(5): 90-98. DOI:10.3969/j.issn.1001-4225.2017.05.018 |
| [4] |
Yan JH, Meng Y, Lu L, et al. Industrial big data in an industry 4.0 environment: Challenges, schemes, and applications for predictive maintenance. IEEE Access, 2017, 5: 23484–23491.
|
| [5] |
张洁, 高亮, 秦威, 等. 大数据驱动的智能车间运行分析与决策方法体系. 计算机集成制造系统, 2016, 22(5): 1220-1229. |
| [6] |
杨枝雨. 基于大数据的印花质量影响因素分析方法研究 [硕士学位论文]. 上海: 东华大学, 2017.
|
| [7] |
李继安, 冯晓荣, 贾世准, 等. 工业大数据与服务大数据及其检测要点对比研究. 电子产品可靠性与环境试验, 2017, 35(S1): 1-6. DOI:10.3969/j.issn.1672-5468.2017.S1.001 |
| [8] |
Yang LP, Wang FZ, Wang T. Analysis of dishonorable behavior on railway online ticketing system based on k-means and FP-growth. Proceedings of 2017 IEEE International Conference on Information and Automation. Macau, China. 2017. 1173–1177.
|
| [9] |
Pfahringer B, Holmes G, Kirkby R. Optimizing the induction of alternating decision trees. Proceedings of the 5th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Hong Kong, China. 2001. 477–487.
|
| [10] |
杨碧姗, 王腾蛟, 常雷, 等. 一种快速可扩展的ADTree构建算法. 计算机研究与发展, 2007, 44(S3): 335-340. |
| [11] |
Watcharapasorn P, Kurubanjerdjit N. The surgical patient mortality rate prediction by machine learning algorithms. Proceedings of the 13th International Joint Conference on Computer Science and Software Engineering. Khon Kaen, Thailand. 2016. 1–5.
|
| [12] |
俞燕. 工业企业生产成本核算中的内部控制措施. 中国经贸, 2014(8): 169-170. DOI:10.3969/j.issn.1009-9972.2014.08.108 |
| [13] |
浦哲, 边慧光. 成型过程对全钢载重子午线轮胎动平衡的影响. 轮胎工业, 2013, 33(6): 364-366. DOI:10.3969/j.issn.1006-8171.2013.06.012 |
| [14] |
陈吉荣, 乐嘉锦. 基于MapReduce的Hadoop大表导入编程模型. 计算机应用, 2013, 33(9): 2486-2489. |
| [15] |
Taleb I, Dssouli R, Serhani MA. Big data pre-processing: A quality framework. Proceedings of 2015 IEEE International Congress on Big Data. New York, NY, USA. 2015. 191–198.
|
| [16] |
Thusoo A, Sarma JS, Jain N, et al. Hive: A warehousing solution over a map-reduce framework. Proceedings of the VLDB Endowment, 2009, 2(2): 1626-1629. DOI:10.14778/1687553 |
| [17] |
Freund Y, Mason L. The alternating decision tree learning algorithm. Proceedings of the 16th International Conference on Machine Learning. San Francisco, CA, USA. 1999. 124–133.
|
| [18] |
孟辛澄. 大数据时代企业市场营销策略探索. 商场现代化, 2018(2): 75-76. |
 2018, Vol. 27
2018, Vol. 27



