曲面细分技术是计算机辅助几何设计(Computer Aided Geometric Design, 简称CAGD)和计算机图形学(Computer Graphics, 简称CG)的研究热点, 该研究成果已经在曲面造型、几何设计和处理、动画软件等方面上广泛应用[1].
给定一个由初始控制顶点构成的网格, 细分规则是根据相应的几何规则和拓扑规则, 在原有的网格上插入新的顶点, 通过不断的重复细分规则, 最终生成一个网格可表示为实体或极限曲面[2,3]. 根据细分曲面是否通过初始控制顶点可以将细分方法分为两类, 分别是逼近型细分和插值型细分[4], 逼近型细分生成的极限曲面相对于初始控制网格会收缩, 但是极限曲面光顺性较好, 相较于逼近型细分, 插值型细分则要求极限曲面通过初始控制网格, 但光顺性不如逼近型细分. 典型的基于四边形网格的逼近型细分代表有Catmull-Clark[5]细分, 生成的极限曲面在规则点处C2连续, 不规则点处C1连续. 典型的插值型细分代表有蝶型细分方法(Butterfly Subdivision), 后来又由Kobbelt等[6]作了改进, 改进的细分方法可以在任意拓扑网格上实现C1连续. 插值型细分方法得到的极限曲面虽然不会收缩, 但是极限曲面可能产生不必要的扭曲, 并且对锐利形状的初始网格更加敏感, 容易产生效果比较差的曲面.
实际应用当中常常要求极限曲面可以通过初始控制顶点, 如何生成极限曲面既光顺, 又能实现插值初始控制网格成为近年来计算机辅助几何设计研究的一个热点, 其中Hoppe[7], Nasri[8], Brunet[9]以及Halstead[10]等提出全局优化方法构造出线性方程组反解控制顶点实现插值, Zheng和Cai[11]提出一种用两步 Catmull-Clark 细分方法构造插值曲面, 上述方法都需求解线性方程组, 对稠密的控制网格难以处理. 随着B样条曲线渐进迭代逼近(Progressive Iterative Approximation, 简称PIA)方法在曲面细分研究方面的推广, Chen等[12]提出了Catmull-Clark细分的渐进迭代插值方法, 上述方法缺少调整曲面造型的自由度. Lin和Pan等[13,14]通过两步细分的方法提出了基于形状控制的插值型 Loop细分和Catmull-Clark 细分, Guo等[15]提出基于渐进插值的 Catmull-Clark 双正交细分小波及其应用, 分析了该算法具有较高的效率和稳定性, 以上方法同时实现了插值和形状控制, 但对于初始控制网格中存在着尖锐的顶点, 仍缺少某些细节特征的处理, 生成的细分曲面效果不够理想.
近年来, Catmull-Clark细分建模方法的应用越来越广泛. Bénard等[16]利用Catmull-Clark细分实现了计算具有精确拓扑的光顺曲面轮廓. Wei等[17]提出了拓展截断层次的Catmull-Clark细分方法, 改进了曲面的局部特征. Wang等[18]利用参数化的二阶Bezier生成插值型Catmull-Clark细分曲面. 实际建模当中, 细分曲面的形状控制起着重要作用, 法向量可以量化的表示模型的某些细节特征, 是曲面形状控制的重要因素, 因此插值法向量对于曲面形状控制有着重要意义, Halstead[10]提出了Catmull-Clark细分的顶点法向量的计算方法, 为了使应用渐进迭代方法生成的Catmull-Clark细分曲面既能实现形状控制, 又能插值法向量, 本文在文献[19]的基础上提出一种基于顶点法向量约束的两步Catmull-Clark细分插值算法, 插值目标是给定一个闭合的初始四边形网格
本文讨论定义在闭合的四边形网格上的Catmull-Clark细分, 几何规则是计算在细分过程中产生的新顶点(分别是新面点F点, 新边点E点, 新顶点V点), 每一次细分后生成的新顶点的拓扑连接规则都保持一致. 为了分析一个顶点周围的极限曲面, 引入两个矩阵来描述局部的细分过程, 分别是顶点的1-领域顶点组成的列矩阵和相应的细分矩阵.
| ${S_4} = \left[ {\begin{aligned} 9&\quad {\displaystyle\frac{3}{2}}&{\displaystyle\frac{3}{2}}&\quad {\displaystyle\frac{3}{2}}&{\displaystyle\frac{3}{2}}&\quad {\displaystyle\frac{1}{4}}&{\displaystyle\frac{1}{4}}&\quad {\displaystyle\frac{1}{4}}&{\displaystyle\frac{1}{4}} \\ 6&\quad 6&1&\quad 0&1&\quad 1&0&\quad 0&1 \\ 6&\quad 1&6&\quad 1&0&\quad 1&1&\quad 0&0 \\ 6&\quad 0&1&\quad 6&1&\quad 0&1&\quad 1&0 \\ 6&\quad 1&0&\quad 1&6&\quad 0&0&\quad 1&1 \\ 4&\quad 4&4&\quad 0&0&\quad 4&0&\quad 0&0 \\ 4&\quad 0&4&\quad 4&0&\quad 0&4&\quad 0&0 \\ 4&\quad 0&0&\quad 4&4&\quad 0&0&\quad 4&0 \\ 4&\quad 4&0&\quad 0&4&\quad 0&0&\quad 0&4 \end{aligned}} \right]*\frac{1}{{16}}$ |
整个细分过程可以表示为对初始控制顶点重复左乘细分矩阵, 因此, 存在一个
Halstead通过对Doo-Sabin细分进行分析获得细分矩阵
引理1[10]. 初始控制网格
Catmull-Clark细分中细分矩阵
| ${v^\infty } = \displaystyle\frac{{{n^2}v + 4\displaystyle\sum\limits_j {{e_j}} + 4\sum\limits_j {{f_j}} }}{{n(n + 5)}}$ | (1) |
次主特征值
| $\begin{aligned}{l_2} = &(0,{A_n}\cos \displaystyle\frac{{2\pi }}{n},{A_n}\cos \frac{{2\pi *2}}{n},\cdots,{A_n}\cos \frac{{2\pi *n}}{n},\\&\cos \displaystyle\frac{{2\pi }}{n} + \cos \frac{{2\pi *2}}{n},\cos \frac{{2\pi *2}}{n} + \cos \frac{{2\pi *3}}{n},\cdots,\\& \cos \displaystyle\frac{{2\pi *n}}{n} + \cos \frac{{2\pi *(n + 1)}}{n}\\ {l_3} = &(0,{A_n}\sin \displaystyle\frac{{2\pi }}{n},{A_n}\sin \frac{{2\pi *2}}{n},\cdots,{A_n}\sin \frac{{2\pi *n}}{n},\\& \sin \displaystyle\frac{{2\pi }}{n} + \sin \frac{{2\pi *2}}{n},\sin \frac{{2\pi *2}}{n} + \sin \frac{{2\pi *3}}{n},\cdots,\\& \sin \frac{{2\pi *n}}{n} + \sin \frac{{2\pi *(n + 1)}}{n}\end{aligned}$ |
其中
| $\begin{aligned}& {n^\infty } = \Bigg\{ \displaystyle\sum\nolimits_j {\Bigg[{A_n}} \cos \frac{{2\pi j}}{n}{e_j} + \left(\cos \frac{{2\pi j}}{n} + \cos \frac{{2\pi (j + 1)}}{n}\right){f_j}\Bigg]\Bigg\} \\ &\quad \quad \times \Bigg\{ \sum\nolimits_j {\Bigg[{A_n}} \sin \frac{{2\pi j}}{n}{e_j} + \left(\sin \frac{{2\pi j}}{n} + \sin \frac{{2\pi (j + 1)}}{n}\right){f_j}\Bigg]\Bigg\}\end{aligned}$ | (2) |
两步Loop细分插值方法在文献[19]中第一次被提出, 本文提出的方法是给定一个初始控制网格
1) 拓扑规则与传统的Catmull-Clark细分方法保持不变;
2) 几何规则中, 新边点和新面点与传统的Catmull-Clark细分方法保持不变. 新顶点的取法修改为:
| ${v^1} = \lambda {v^0} + (1 - \lambda )[\alpha { E} + (1 - \alpha ){ F}]$ | (3) |
其中,
第二个步骤是调整控制网格
| $v_\infty ^1 = \displaystyle\frac{{({n^2}\lambda + 7n/4){v^1} + {\beta _n}\displaystyle\sum\nolimits_{i = 1}^n {e_i^1 + \frac{3}{{10}}{\beta _n}\sum\nolimits_{i = 1}^n {f_i^1} } }}{{n(n + 5)}}$ |
其中,
| $\begin{aligned}{d^{k + 1}} & = {v^0} - v_\infty ^{k + 1} = {v^0} - \displaystyle\frac{{\left({n^2}\lambda + \displaystyle\frac{7}{4}n\right){v^{k + 1}} + \left[n\left(1 - \lambda \right)\displaystyle\frac{{10}}{{13}} + \displaystyle\frac{5}{2}\right]\sum\nolimits_i {e_i^{k + 1}} + \left[n\left(1 - \lambda \right)\displaystyle\frac{3}{{13}} + \displaystyle\frac{3}{4}\right]\sum\nolimits_i {f_i^{k + 1}} }}{{n\left(n + 5\right)}}\\ & = {d^k} -\displaystyle\frac{{\left({n^2}\lambda + \displaystyle\frac{7}{4}n\right){d^k} + \left[n\left(1 - \lambda \right)\displaystyle\frac{{10}}{{13}} + \displaystyle\frac{5}{2}\right]\sum\nolimits_i {d_{e_i^k}^k} + \left[n\left(1 - \lambda \right)\displaystyle\frac{3}{{13}} + \displaystyle\frac{3}{4}\right]\sum\nolimits_i {d_{f_i^k}^k} }}{{n\left(n + 5\right)}} = 0\end{aligned}$ |
第二步是调整新边点
要证明第2节给出的两步Catmull-Clark细分的初始控制顶点法向量插值, 就是要确定差向量
设网格
| $\begin{array}{l}{C_2} = \displaystyle\sum\nolimits_{i = 1}^n {\Bigg[{A_n}\cos \frac{{2\pi i}}{n}} e_i^1 + \left(\cos \frac{{2\pi i}}{n} + \cos \frac{{2\pi (i + 1)}}{n}\right)f_i^1\Bigg]\\{C_3} = \displaystyle\sum\nolimits_{i = 1}^n {\Bigg[{A_n}\sin \frac{{2\pi i}}{n}} e_i^1 + \left(\sin \frac{{2\pi i}}{n} + \sin \frac{{2\pi (i + 1)}}{n}\right)f_i^1\Bigg]\end{array}$ |
其中,
实现初始控制顶点法向量插值的关键是调整网格
| $\begin{aligned}\widetilde N &= \{ 0*{v^1} + \sum\nolimits_{i = 1}^n {\left[ {{A_n}\cos \frac{{2\pi i}}{n}\left(e_i^1 + {\delta _i}\right) + \left(\cos \frac{{2\pi i}}{n} + \cos \frac{{2\pi (i + 1)}}{n}\right)} \right.} \Bigg.\Bigg. {\left(f_i^1 + {\delta _i}\right)} \Bigg]\Bigg\} \\&\;\;\;\;\times\Bigg\{ 0*{v^1} +\sum\nolimits_{i = 1}^n {\left[ {{A_n}\sin \frac{{2\pi i}}{n}\left(e_i^1 + {\delta _i}\right) } \right.} + \left(\sin \frac{{2\pi i}}{n} + \sin \frac{{2\pi (i + 1)}}{n}\right) \left. {\left. {\left(f_i^1 + {\delta _i}\right)} \right]} \right\} \\&=\Bigg\{ {C_2} + \sum\nolimits_{i = 1}^n {\left. {{A_n}\cos \frac{{2\pi i}}{n}{\delta _i}} \right]} \Bigg\} + \left(\cos \frac{{2\pi i}}{n} + \cos \frac{{2\pi (i + 1)}}{n}\right){\delta _i}\times\Bigg\{ {C_3} + \sum\nolimits_{i = 1}^n {\Bigg[{A_n}\sin \frac{{2\pi i}}{n}{\delta _i} + \left(\sin \frac{{2\pi i}}{n} + \sin \frac{{2\pi (i + 1)}}{n}\right){\delta _i}\Bigg]} \Bigg\} \\&= \Bigg({C_2} + \sum\nolimits_{i = 1}^n {{a_i}{\delta _i}\Bigg) \times } \Bigg({C_3} + \sum\nolimits_{i = 1}^n {{b_i}{\delta _i}\Bigg)} \\ &{a_i} = \sum\nolimits_{i = 1}^n {\Bigg[{A_n}\cos \frac{{2\pi i}}{n} + \Bigg(\cos \frac{{2\pi i}}{n} + \cos \frac{{2\pi (i + 1)}}{n}\Bigg)\Bigg]} ,\; {b_i} = \sum\nolimits_{i = 1}^n {\Bigg[{A_n}\sin \frac{{2\pi i}}{n} + \Bigg(\sin \frac{{2\pi i}}{n} + \sin \frac{{2\pi (i + 1)}}{n}\Bigg)\Bigg]} \end{aligned}$ | (4) |
要使
| $({C_2} + \sum\nolimits_{i = 1}^n {{a_i}} {\delta _i}) \bot {N^\infty }$ | (5) |
| $({C_3} + \sum\nolimits_{i = 1}^n {{b_i}} {\delta _i}) \bot {N^\infty }$ | (6) |
上述差向量
| $\min \;\;\; \sum\nolimits_{i = 1}^n {{\delta _i}*} {\delta _i}$ | (7) |
s.t.
| $({C_2} + \sum\nolimits_{i = 1}^n {{a_i}} {\delta _i})*{N^\infty } = 0$ | (8) |
| $({C_3} + \sum\nolimits_{i = 1}^n {{b_i}} {\delta _i})*{N^\infty } = 0$ | (9) |
这里采用拉格朗日乘子法求解上述问题, 引入两个拉格朗日乘子
| $\begin{gathered} F = \sum\nolimits_{i = 1}^n {{\delta _i}*{\delta _i} + {\omega _1}} ({C_2} + \sum\nolimits_{i = 1}^n {{a_i}} {\delta _i})*{N^\infty } \hfill \\ \quad + {\omega _1}({C_3} + \sum\nolimits_{i = 1}^n {{b_i}} {\delta _i})*{N^\infty } \hfill \\ \end{gathered} $ |
让
| $\frac{{dF}}{{d{\delta _k}}} = 2{\delta _k} + {\omega _1}{a_k}{N^\infty } + {\omega _2}{b_k}{N^\infty } = 0,(k = 1,2,\cdots,n)$ | (10) |
求得:
| ${\delta _k} = - \frac{1}{2}({\omega _1}{a_k}{N^\infty } + {\omega _2}{b_k}{N^\infty })$ | (11) |
将式(11)代入式(8)和式(9)中得:
| $2{C_2}*{N^\infty } - {\omega _1}\sum\nolimits_{i = 1}^n {a_i^2} {N^{\infty 2}} - {\omega _2}\sum\nolimits_{i = 1}^n {{a_i}{b_i}} {N^{\infty 2}} = 0$ |
| $2{C_3}*{N^\infty } - {\omega _1}\sum\nolimits_{i = 1}^n {{a_i}{b_i}} {N^{\infty 2}} - {\omega _2}\sum\nolimits_{i = 1}^n {b_i^2} {N^{\infty 2}} = 0$ |
由于本文讨论闭合的四边形网格上的 Catmull-Clark 细分, 则网格上每个顶点的度
| ${\omega _1} = \frac{{2{C_2}*{N^\infty }}}{{\displaystyle\sum\nolimits_{i = 1}^n {a_i^2} {N^{\infty 2}}}}$ |
| ${\omega _2} = \frac{{2{C_3}*{N^\infty }}}{{\displaystyle\sum\nolimits_{i = 1}^n {b_i^2} {N^{\infty 2}}}}$ |
得到新边点和新面点的差向量为:
| ${\delta _k} = - \frac{1}{2}\left(\frac{{2{C_2}*{N^\infty }}}{{\displaystyle\sum\nolimits_{i = 1}^n {a_i^2} {N^{\infty 2}}}}{a_k} + \frac{{2{C_3}*{N^\infty }}}{{\displaystyle\sum\nolimits_{i = 1}^n {b_i^2} {N^{\infty 2}}}}{b_k}\right){N^\infty }$ |
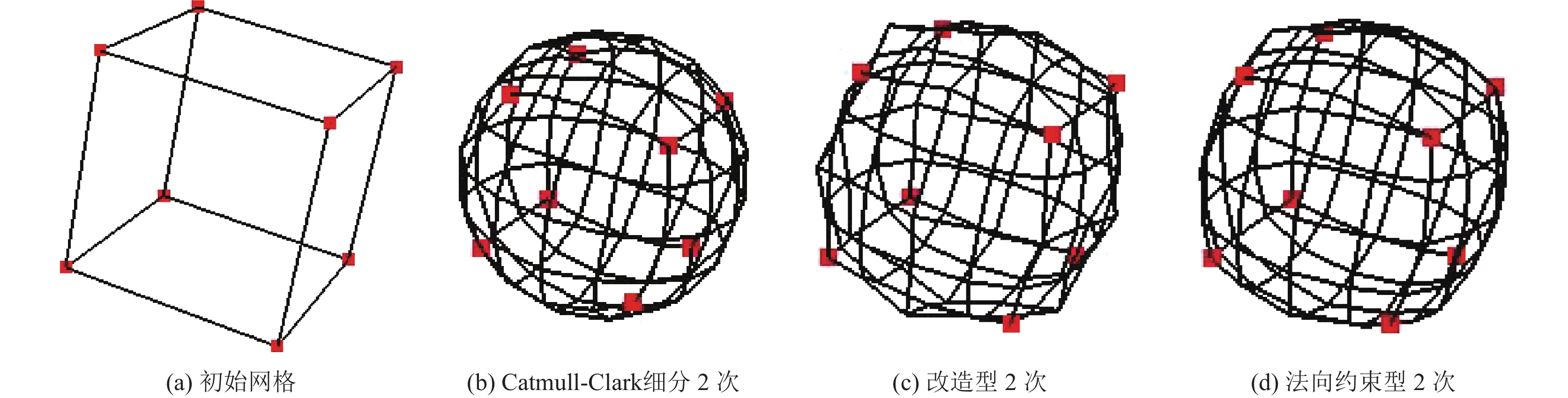
本文利用 Visual Studio 2012 和 CSGL 实现了基于顶点法向量约束的两步Catmull-Clark细分插值方法. 本文给出了4个四边形网格模型的例子, 各个顶点处形状控制参数值都取
|
图 1 基于顶点法向量约束的两步Catmull-Clark细分插值方法(正方体形) |

|
图 2 基于顶点法向量约束的两步Catmull-Clark细分插值方法(圆环形) |
|
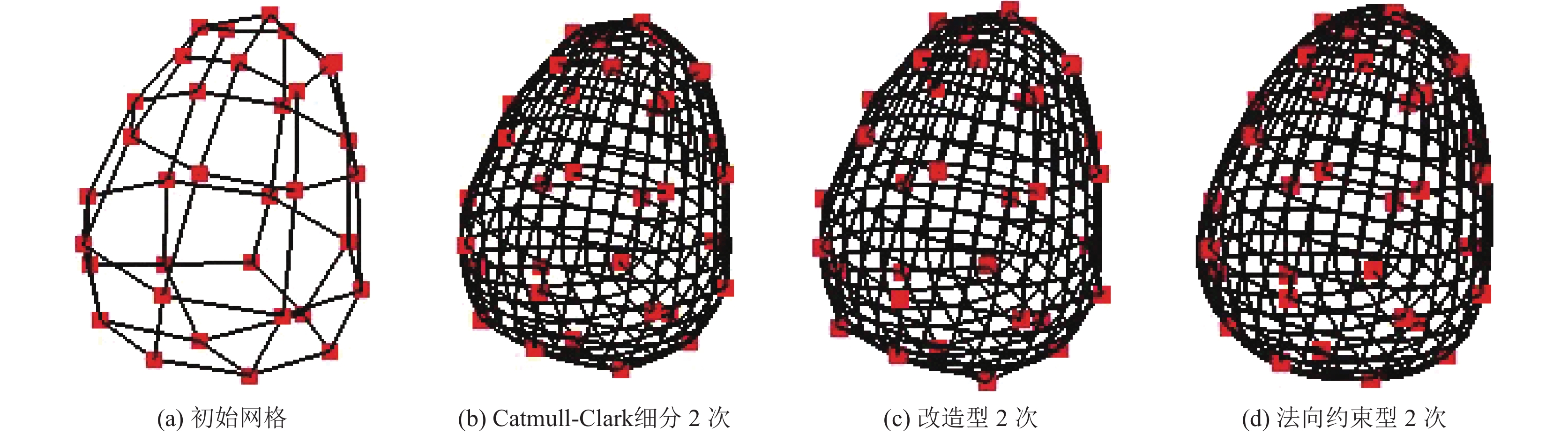
图 3 基于顶点法向量约束的两步Catmull-Clark细分插值方法(圆锥形) |
|
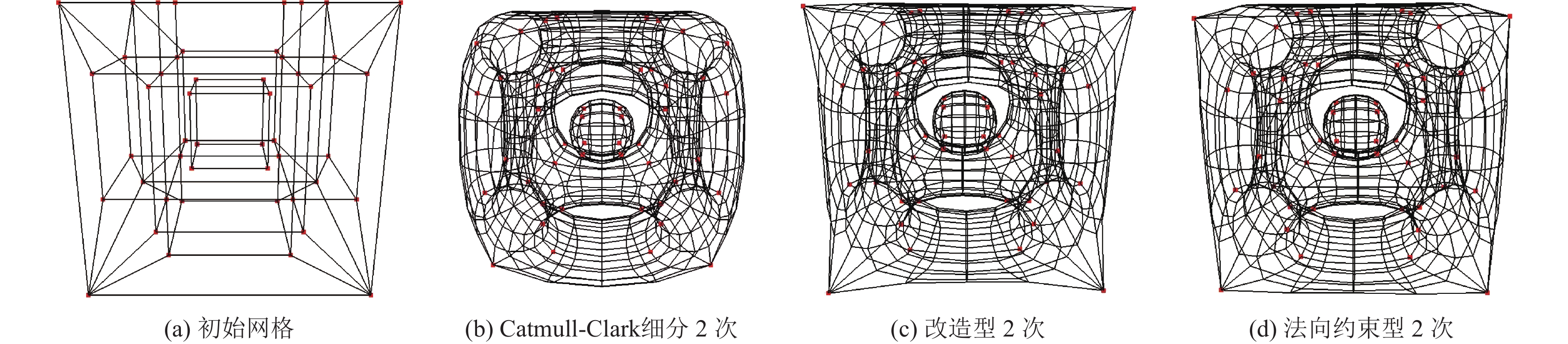
图 4 基于顶点法向量约束的两步Catmull-Clark细分插值方法(正方体与球形) |
5 结语
本文提出了一种基于顶点法向量约束的两步Catmull-Clark细分插值方法, 该方法在改造型 Catmull-Clark 细分规则基础上结合初始控制顶点法向量的约束实现对 Catmull-Clark 细分生成曲面的插值, 引入拉格朗日乘子法求出乘子, 从而求出差向量实现插值法向量. 该方法同时具有形状调整和插值法向量两个特性, 丰富了细分曲面造型的形状控制方法. 本文方法只研究了实验图形的效果, 还可以继续研究细分的精度和效率.
| [1] |
林淑金. 插值逼近融合的曲面造型方法研究与应用[博士学位论文]. 广州: 中山大学, 2008.
|
| [2] |
Hassan MF, Ivrissimitzis IP, Dodgson NA, et al. An interpolating 4-point C2 ternary stationary subdivision scheme. Computer Aided Geometric Design, 2002, 19(1): 1-18. DOI:10.1016/S0167-8396(01)00084-X |
| [3] |
Shi Z, Lin SJ, Luo XN, et al. Interpolatory and mixed loop schemes. Computer Graphics Forum, 2008, 27(7): 1829-1835. DOI:10.1111/cgf.2008.27.issue-7 |
| [4] |
王国瑾, 汪国昭, 郑建民. 计算机辅助几何设计. 北京: 高等教育出版社, 2001.
|
| [5] |
Catmull E, Clark J. Recursively generated B-spline surfaces on arbitrary topological meshes. Computer-Aided Design, 1978, 10(6): 350-355. DOI:10.1016/0010-4485(78)90110-0 |
| [6] |
Kobbelt L. Interpolatory subdivision on open quadrilateral nets with arbitrary topology. Computer Graphics Forum, 1996, 15(3): 409-420. DOI:10.1111/cgf.1996.15.issue-3 |
| [7] |
Hoppe H, DeRose T, Duchamp M, et al. Piecewise smooth surface reconstruction. Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques. New York, NY, USA. 1994. 295–302.
|
| [8] |
Nasri AH. Polyhedral subdivision methods for free-form surfaces. ACM Transactions on Graphics, 1987, 6(1): 29-73. DOI:10.1145/27625.27628 |
| [9] |
Brunet P. Including shape handles in recursive subdivision surfaces. Computer Aided Geometric Design, 1988, 5(1): 41-50. DOI:10.1016/0167-8396(88)90019-2 |
| [10] |
Halstead M, Kass M, DeRose T. Efficient, fair interpolation using Catmull-Clark surfaces. Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques. Anaheim, CA, USA. 1993. 35–44.
|
| [11] |
Zheng J, Cai Y. Interpolation over arbitrary topology meshes using a two-phase subdivision scheme. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(3): 301-310. DOI:10.1109/TVCG.2006.49 |
| [12] |
Chen ZX, Luo XN, Tan L, et al. Progressive interpolation based on Catmull-Clark subdivision surfaces. Computer Graphics Forum, 2008, 27(7): 1823-1827. DOI:10.1111/cgf.2008.27.issue-7 |
| [13] |
林晓晶, 潘日晶. 一种基于Loop细分的渐进插值方法. 福建师范大学学报(自然科学版), 2014, 30(1): 18-24. |
| [14] |
林传銮, 潘日晶, 陈青, 等. 基于形状控制的细分曲面的局部渐进插值方法. 计算机系统应用, 2015, 24(7): 104-110. DOI:10.3969/j.issn.1003-3254.2015.07.019 |
| [15] |
郭华源, 秦开怀, 孙丰. 基于渐进插值的Catmull-Clark双正交细分小波及其应用. 计算机辅助设计与图形学学报, 2017, 29(6): 1118-1127. DOI:10.3969/j.issn.1003-9775.2017.06.018 |
| [16] |
Bénard P, Hertzmann A, Kass M. Computing smooth surface contours with accurate topology. ACM Transactions on Graphics, 2014, 33(2): 19. |
| [17] |
Wei XD, Zhang YJ, Hughes TJR, et al. Extended truncated hierarchical Catmull-Clark subdivision. Computer Methods in Applied Mechanics and Engineering, 2016, 299: 316-336. DOI:10.1016/j.cma.2015.10.024 |
| [18] |
Wang JZ, Cheng FH. G2 Interpolation for polar surfaces. Computer-Aided Design and Applications, 2016, 13(5): 610-617. DOI:10.1080/16864360.2016.1150705 |
| [19] |
林晓晶. 基于三角网格逼近型细分的插值方法[硕士学位论文]. 福州: 福建师范大学, 2014.
|
 2018, Vol. 27
2018, Vol. 27



