中国聚变工程实验堆(CFETR)是正在设计中的超导聚变实验堆, 旨在弥补聚变实验堆ITER和示范反应堆DEMO之间的空白^[1–3]. 为了支持CFETR设计工作高效协同的展开, CFETR集成设计平台^[4,5]目前正在开发中.

在工程设计中, 由于外部环境等因素影响, 部件会产生应力、导致形变, 影响零部件的装配设计与空间布局^[6]. 因此对形变部件的碰撞检测, 是工程设计中的必不可少的检测环节. 工程设计中通常利用有限元方法分析计算部件的应力、形变, 计算结果以有限元网格的形式存储. 目前对于刚体模型的碰撞检测算法研究比较充分, 针对复杂场景的快速检测算法也正在不断发展^[7]. 对有限元结果的碰撞检测, 由于模型的复杂度较高, 需要采取多种措施降低计算复杂度.

对形变的有限元模型的碰撞检测问题, Sean Curtis等提出了基于特征三角形的快速检测方法^[8], 吴峥等提出了三角片与包围盒混合的快速碰撞检测算法^[9]. 这些算法主要针对三角片网格与四面体网格, 不适合工程设计中复杂多样的有限元网格, 且在三角形相交、包围盒处理、并行化等方面存在不足, 计算的效率存在提升空间.

本文提出了一种基于三角形碰撞检测与轴对齐包围盒(Axis-Aligned Bounding Box, AABB)的、针对有限元模型的通用快速碰撞检测算法: 将有限元的几何表面三角化后, 选择合适的三角形相交算法, 利用AABB包围盒紧密性好、相交测试简单的优势并采用优化后的AABB树算法, 结合并行化的设计, 实现对有限元模型的快速碰撞检测. 利用本算法可以处理多种有限元网格, 对工程设计中复杂的形变有限元模型实现高效快速的碰撞检测. 本文将该算法应用于聚变堆的工程设计中, 能够有效提高碰撞检测的效率, 并给出清晰直观的检测结果.

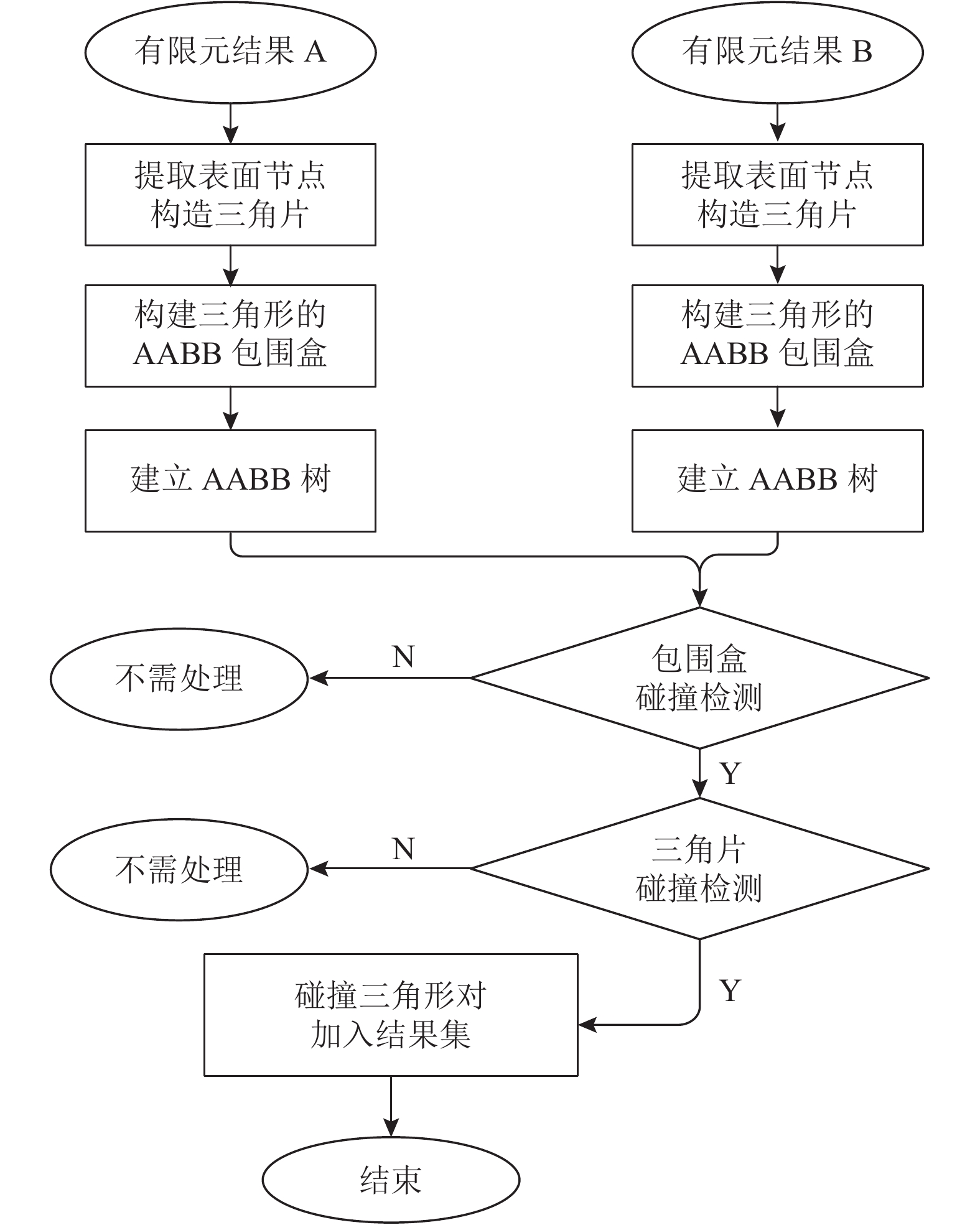
1 碰撞检测算法

有限元模型由大规模的网格和网格节点组成, 网格类型包括四面体、六面体等几何体. 在有限元模型的碰撞检测中, 通过提取几何表面、将表面的几何面用三角形重构, 可以将有限元模型的碰撞问题, 转换为表面三角片的碰撞检测问题; 同时利用包围盒算法简化碰撞计算、引入AABB树算法提高碰撞检测效率^[10], 最终实现部件有限元模型的快速碰撞检测. 算法的处理步骤如图1所示.

核心步骤如下所述:

Step 1. 读取有限元计算结果, 提取模型的表面节点, 用三角片重构, 以三角形网格描述几何体的轮廓.

Step 2. 计算三角片对应的AABB包围盒, 将包围盒与三角形对应.

Step 3. 对包围盒集, 构造AABB树, 将所有包围盒存储在二叉树中.

Step 4. 对两棵AABB树中的包围盒进行碰撞检测. 如果包围盒间存在碰撞, 则继续检测包围盒对应的三角片的碰撞问题.

Step 5. 跳过未碰撞的包围盒、三角片, 记录所有碰撞的三角片对, 构成碰撞结果集.

Step 6. 结束计算, 将碰撞区域存储为STL (stereolithography, 立体光刻)格式的三角片模型文件.

1.1 包围盒算法

包围盒算法在数字化模型的碰撞检测计算中有着广泛的应用^[11,12], 其核心思路为: 将复杂几何体用一个简单几何体包围, 如立方体、球体, 然后计算简单几何体的碰撞, 排除不碰撞对象, 最后计算被简单几何体包含的几何体间关系.

针对本文静态检测的场景, 选择构造AABB包围盒进行计算. 在读取三角片网格后, 首先对所有三角片构造AABB包围盒, 即用一个与x、y、z三轴平行的立方体包围几何面. 如果一对立方体不碰撞, 则立方体内的几何面元不会碰撞.

对一个三角形面元, 其包围盒可以两个点表示: 如式(1)(2)所示, 两个点的坐标由所有顶点在x、y、z方向上的最大值最小值决定.

${{\rm{P}}_{\max }} = {x_{\max }}\vec i + {y_{\max }}\vec j + {z_{\max }}\vec k$

(1)

${{\rm{P}}_{\min }} = {x_{\min }}\vec i + {y_{\min }}\vec j + {z_{\min }}\vec k$

(2)

检测两个轴对齐包围盒是否碰撞, 需要将包围盒分别投影到x、y、z轴上, 判断其投影是否相交. 对于两个包围盒A、B, 将其投影到x轴上, 对应关系为:

$A \to ({x_{a - \min }},{x_{a - \max }})$

(3)

${\rm{B}} \to ({x_{{{b}} - \min }},{x_{b - \max }})$

(4)

式(3)(4)表示包围盒在x轴上的投影区间, 两区间不相交的条件为式(5):

$({x_{a - \min }} > {x_{b - \max }})||({x_{a - \max }} < {x_{b - \min }})$

(5)

当包围盒在x、y、z轴向的投影都相交, 则判定包围盒相交. 本方法只需进行6次大小判断、3次或操作, 即可完成包围盒碰撞检测.

相比直接进行空间三角形的检测, AABB包围盒排除相交的计算量更小, 因此计算速度更快.

1.2 AABB树算法 1.2.1 层次包围盒与AABB树

当两个三角形相距较远时, 采用AABB包围盒可以快速排除且降低了求交的计算量, 但是采用AABB包围盒算法, 依然需要对A的m个包围盒与B的n个包围盒求交, 没有降低求交计算的次数.

为了降低求交计算的时间复杂度, 引入AABB树的结构. AABB树基于层次包围盒原理, 即用大的包围盒包裹小的层次包围盒, 并用大包围盒进行求交计算; 层次包围盒基于如下原理:

对集合A、B与P, 存在 ${\rm{A}} \in {\rm{P}}$ , ${\rm{B}} \in {\rm{P}}$ , 如果 ${\rm{Q}} \cap {\rm{P = }}\emptyset $ , 则 ${\rm{Q}} \cap {\rm{A = Q}} \cap {\rm{B = }}\emptyset $ . 因此如果大包围盒与某个包围盒不相交, 则其中包含的包围盒也不相交; 如此可以降低求交的次数.

AABB树是一种以二叉树存储的层次包围盒, 树的每个节点都是一个包围盒, 除叶节点外每个包围盒包含两个子盒; 所有叶节点为几何体的包围盒.

AABB树的层次包围盒结构如图2所示, 对应的二叉树存储结构如图3所示.

1.2.2 AABB树的构建

AABB树的构建流程如图4, 核心步骤如下文.

(1) 新建包围盒作为节点, 包含两个子节点的包围盒.

(2) 新包围盒向树中添加时, 与节点包围盒测试相交.

(3) 如果不相交则新建包围盒包裹当前节点和新包围盒并作为头结点, 当前节点和新包围盒作为子节点.

(4) 如果与其相交, 则首先新建大包围盒替换当前节点, 然后新包围盒与两个子节点合并, 选择合并后体积较小的节点, 进行迭代操作.

通过这种方法, 可以建立层次包围盒结构, 并存储在二叉树中.

1.2.3 AABB树的碰撞检测

一个包围盒, 与一棵AABB树的碰撞检测过程, 从根节点对应的包围盒开始计算:

(1) 如果与节点不相交, 则该节点的所有子节点都不相交.

(2)如果包围盒与一个节点相交, 则继续与节点的两个子节点求交, 进行迭代直到叶节点. 理想情况下, 包围盒每次只与一个子包围盒相交, 相当于二分查找. 对于n个节点的树, 理想情况下的求交次数为logn级别.

因此采用AABB树后, 算法复杂度可以降低为O(mlogn).

对两棵AABB树的计算有所区别: 从两棵树的根节点开始遍历, 如果当前两个节点相交, 则计算二者的子节点包围盒的相交关系; 通过递归, 直到叶节点包围盒为止.

1.2.4 AABB树的优化

王晓荣等从AABB树的平衡角度, 提出了AABB树构建过程中的建议^[13]. 当AABB树的左右节点近似于空间二分时, 碰撞检测的效率最高; 为了实现这个效果, 引入分割操作:

(1)选择整个模型在x、y、z轴上最长的轴, 计算模型在该方向的最大值、最小值.

(2)将所有包围盒, 按照其在最长轴上的投影, 在最小值、最大值方向分成两组, 并尽可能保证平衡.

通过这种方法, 直到二分后每一组的三角片数量到达一定程度; 如此建立的二叉树比不分组情况下更加平衡, 计算效率更高.

1.3 三角形相交检测

对于三角形的快速相交检测算法研究很多, 典型的如标量判别型的Möller算法^[14], 矢量判别型的Devillers & Guigue算法 ^[15](以下简称Devillers算法). 本节将对两种算法进行比较, 选择本计算场景下性能更优的算法.

1.3.1 标量判别型的Möller算法

标量判别型算法是通过准确计算来获知两三角形相交关系的一类算法. 算法的基本思路如下所述:

设有两个三角形 ${{\rm{T}}_1}$ 和T₂, 顶点分别为V₁₀、V₁₁、V₁₂与V₂₀、V₂₁、V₂₂, 三角形所在的平面分别为 ${S_1}$ 、 ${S_2}$ , 法向量为 ${{{N}}_1}$ 、 ${{{N}}_2}$ , 则有 ${S_1}$ 的方程表示:

${{{N}}_1} \times (x - {V_{10}}){\rm{ = }}0$

(6)

其中, x为任意一点的坐标.

空间中一点坐标带入方程, 值为0则在面上, 大于0则在面上方, 小于0则在面下方. 据此进行如下计算.

Step 1. 计算 ${{\rm{T}}_2}$ 的三个顶点在 ${S_1}$ 平面方程的值.

Step 2. 如果 ${{\rm{T}}_2}$ 三点在 ${S_1}$ 平面同侧, 则不相交.

Step 3. 如果T₂三点在 ${S_1}$ 平面上, 转换为共面三角形的相交计算. 如果一个点在面上, 且其它两点同号, 则计算该点是否在三角形内部; 如果两个点在面上, 计算线段与三角形的关系. 总之, 可以转换为平面内计算.

Step 4. 如果T₂的三个顶点在 ${S_1}$ 的两侧, 则计算 ${{\rm{T}}_1}$ 的三个顶点与 ${S_2}$ 平面的关系.

Step 5. 经过排除计算, 只剩下 ${{\rm{T}}_1}$ 、T₂在两侧的情况.

如图4所示, 设平面的交线为k, 则两个三角形一定都与k相交. 直线k的方程可以表示为:

$k = K \times i + O$

(7)

其中K为直线的方向向量, i为标量化的点坐标.

Möller算法的核心, 就是计算出三角形与k的交点的i值. 设T₁和T₂与k的交点参数值分别为i、j和k、l, 则区间(i, j)与(k, l)相交, 等价于三角形相交.

1.3.2 矢量判别型的Devillers算法

矢量判别型算法是通过一系列计算值的符号来判定两个三角形的位置关系, 继而判别其相交情况的一类算法. 算法的核心思想如下所述:

设空间中四点坐标分别为 $({a_x},{a_y},{a_z})$ , $({b_x},{b_y},{b_z})$ , $({c_x},{c_y},{c_z})$ , $({d_x},{d_y},{d_z})$ , 则有行列式:

$\left[ {{{a}},b,c,d} \right] = \left( {\begin{array}{*{20}{c}} {{a_x}}&{{a_y}}&{{a_z}}&1 \\ {{b_x}}&{{b_y}}&{{b_z}}&1 \\ {{c_x}}&{{c_y}}&{{c_z}}&1 \\ {{d_x}}&{{d_y}}&{{d_z}}&1 \end{array}} \right)$

(8)

行列式的值表示点d与a、b、c组成平面的位置关系, 等于0在面上, 大于0在面上方, 小于0在面的下方. 通过该公式, 对三角形间的位置关系进行判定.

与Möller算法的过程类似, 对于三角形在平面一侧的情况可以进行排除、对于共面或者点、线段等情况可以进行计算; 通过T₁、T₂的最终校验, 最终需要计算剩下T₁、T₂分别在平面两侧的情况.

Devillers算法不计算具体的交点坐标, 而是计算行列式的值, 进行相交判断. 如图所示得情况下, 循环置换顶点, 保证 ${{{V}}_{10}}$ ( ${{{V}}_{20}}$ )在面 ${S_2}$ ( ${S_1}$ )的一面, 同时交换V₁₁、V₁₂( ${{{V}}_{21}}$ 、 ${{{V}}_{22}}$ ), 保证 ${{{V}}_{10}}$ ( ${{{V}}_{20}}$ )在面的上方.

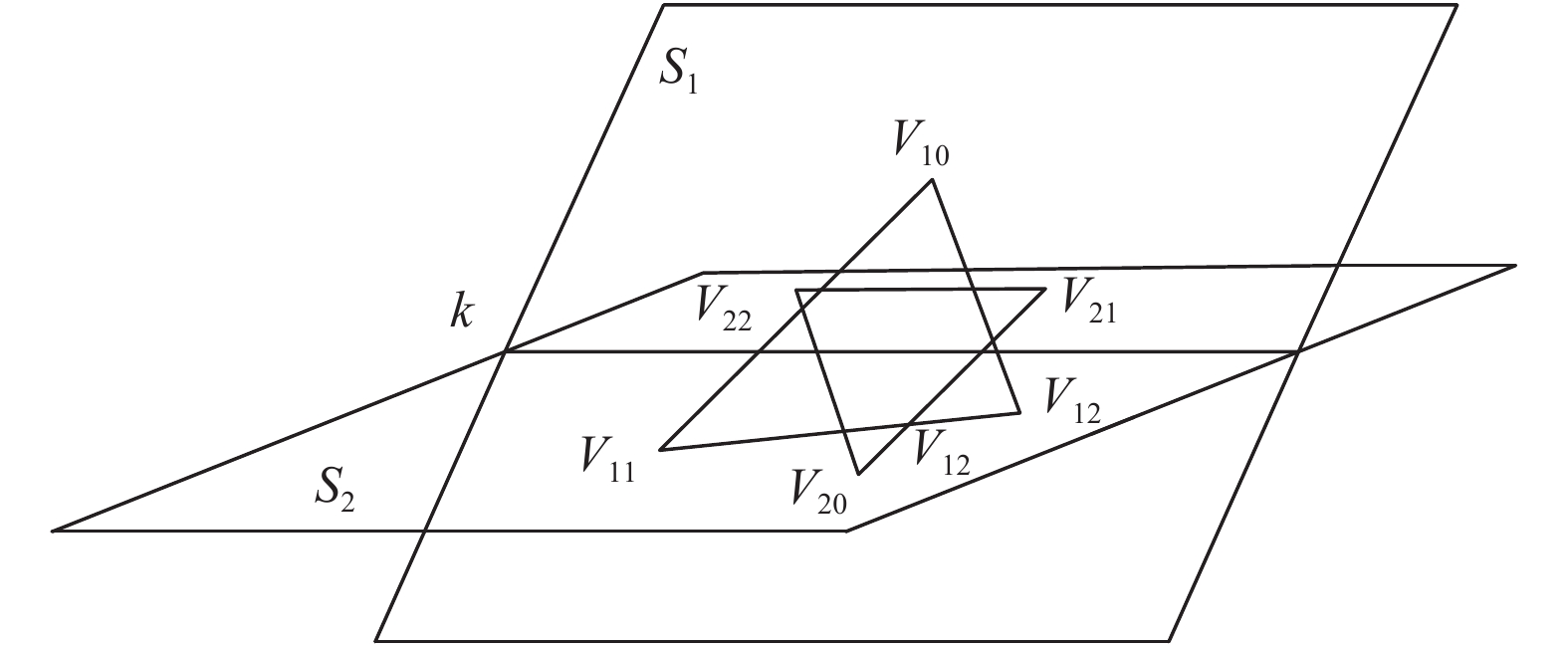
如图5所示, 考虑三角形与交线k的相交区域, 为保证二者存在重叠, 即区间(i, j)与(k, l)相交, 只需k ≤ j且i ≤ l, 用判别式表示即:

$\left[ {{{{V}}_{10}}{{,}}{{{V}}_{11}}{{,}}{{{V}}_{20}}{\rm{,}}{{{V}}_{21}}} \right] \leqslant 0 \cap \left[ {{{{V}}_{10}}{\rm{,}}{{{V}}_{12}}{\rm{,}}{{{V}}_{22}}{\rm{,}}{{{V}}_{20}}} \right] \leqslant 0$

(9)

1.3.3 算法比较

矢量型的Devillers算法, 与标量型的Möller算法相比, 存在性能优势:

(1)内存使用上, Möller算法使用55个变量, 而Devillers算法只需18个变量.

(2)在计算点与面的关系时, 面方程方法与行列式方法计算量相同; 两种算法的区别在处理三角形在两侧的场景下, Möller算法要求解四个坐标的值, 而Devillers算法只判断两个行列式大小, 后者计算量更小.

(3)排除不相交的三角形时, Möller算法进行三次排除, 而Devillers算法进行四次排除; 前两次排除的计算相同, Devillers算法在后面的排除中, 通过行列式的正负号排除, 比Möller算法效率更高.

邹益胜等对两种算法进行了性能测试^[16], 用随机生成的三角形进行计算, 结果表明Devillers算法的计算效率比Möller算法高约15%. 因此本文选择Devillers算法, 对三角形进行相交检测.

1.4 并行优化

实际应用场景中, 复杂模型的三角片网格一般为十万、百万量级, 为了充分利用计算资源, 加快计算速度, 本算法采用多线程的方式, 提高碰撞检测的计算效率.

在文件读取、包围盒构建、AABB树构建过程中, 处理两个模型, 可以利用2个线程并行完成.

在碰撞检测的过程中, 可以将待检测的模型拆分, 利用多线程方法加快计算速度. 设有两棵AABB树A与B, 并行的基本思路如下所述:

(1)根据计算机核心数确定线程数, 一般为 ${2^{{n}}}$ .

(2)将二叉树A, 从头结点开始迭代, 按左右节点拆分为2ⁿ棵子树.

(3)在每个线程中, 每棵子树与二叉树B进行碰撞检测; 全部计算结束后合并结果.

并行没有降低计算量, 而是充分利用多核优势, 缩短碰撞检测需要的时间.

2 算法应用与分析

本文选择CFETR中两个相邻部件作为测试用例, 对算法性能进行测试. 待分析模型为有限元模型, 经三角化处理后重构为三角片网格模型.

算法由C++代码实现, 程序的运行平台为Windows 10系统, 硬件参数为: CPU参数4核3.30 GHz, 内存8 GB.

2.1 算法效率

待处理模型的基本参数, 包括三角形面元、碰撞三角形、碰撞区域占比等参数如表1所示.

为比较算法的性能与优化效果, 在碰撞检测过程中, 使用多种不同策略进行计算:

(1)采用Möller算法遍历计算三角形相交.

(2)采用Devillers算法遍历计算三角形相交.

(3)在方法2基础上, 为三角形建立包围盒, 先对包围盒测试相交, 再计算三角形相交.

(4)在方法3基础上引入AABB树方法, 计算包围盒相交, 然后求解三角形相交.

(5)对方法4中AABB树的构建进行优化.

(6)在5基础上, 采用并行计算加速; 本文中选择4线程进行计算.

采用不同策略时, 算法的性能如表2所示.

对多种优化策略的比较如下:

(1) 三角形相交算法

设A与B模型分别包含m、n个三角形, 在计算碰撞时, 如果采用直接遍历方法, 对A中的每一个三角形, 与B中每一个三角形进行相交测试, 相交测试的次数为m×n, 时间复杂度为O(mn). 策略1与策略2相比, 计算复杂度相同. 实验中1与2的对比表明, 矢量判别型的Devillers算法比标量判别型的Möller算法效率高20%左右.

(2) AABB包围盒

在有限元计算的场景中, 每个三角片面积很小, 三角形间不相交是大概率事件. 采用AABB包围盒算法时, 依然需要将A中m个包围盒与B中n个求交, 计算次数为 $m \times n$ , 时间复杂度为O(mn); 但是AABB包围盒可以将减少每次排除相交的计算量: AABB包围盒只需要最多9次计算可以排除相交, 而Devillers算法在排除相交时, 最少需要进行43次计算. 实验结果表明, 采用AABB包围盒, 相比直接进行三角形相交测试, 可以减少30%左右的计算时间.

(3) AABB树

采用层次包围盒算法时, 考虑理想情况下, 包围盒与一棵n个叶子的二叉树求交时, 每次在两个子节点中只与一个相交, 则只需要 $\log _2n$ 次查询, 因此层次包围盒算法的时间复杂度为O(mlog₂n). 在实际的二叉树建立过程中, 由于包围盒的位置随机分布, 导致建立的二叉树平衡性较差, 复杂度高于到log₂n级别. 3与4的对比显示, 采用AABB树可以降低计算耗时的量级.

(4) 优化的AABB树

方法4与5的对比说明, 采取空间划分的方式对包围盒进行二分, 通过提高二叉树的平衡性, 可以优化AABB树的结构, 从而降低求交的次数. 实验表明, 采取优化的AABB树, 相比不优化情况下碰撞检测的时间降低60%以上.

(5) 并行计算

方法6采用并行方法进行计算, 利用多个线程, 进行二叉树构建、AABB树的碰撞检测. 本次实验中, 并行方法可以将计算耗时降低30%左右.

2.2 算法应用

将该快速碰撞检测算法应用于CFETR的部件检测中, 所得计算结果如图6所示.

在实际工程设计中通常使用建模软件CATIA进行数字化建模、碰撞检测, 因此本文选择CATIA的碰撞计算结果进行对比. CATIA的计算结果如图7所示.

碰撞计算结果的对比显示, 快速检测算法给出的碰撞区域与CATIA计算结果基本一致. CATIA计算碰撞时计算区域的交线, 而算法简化为计算碰撞的三角面对, 大幅提高效率的同时, 能够给出可靠的结果.

在实际设计计算中, 有限元模型的网格数量往往在百万、千万量级, 此时算法的处理效率更加重要.

本文通过将模型B进行网格重, 衡量算法处理大规模网格时的性能.

模型的网格面数量和计算耗时对比如表3所示.

实验结果表明, 本文提出的快速检测算法在处理复杂有限元网格时, 相比CATIA的计算, 效率上存在明显优势. 将本文提出的算法应用在聚变堆工程设计中, 可以大幅缩短计算时间, 提高了工程设计的效率.

3 结论

针对工程设计中存在的有限元模型碰撞问题, 本文设计并实现了一种基于三角形相交检测、AABB包围盒的快速碰撞检测算法, 通过采用三角形的Devillers算法、优化的AABB树和并行化设计, 实现高效的碰撞检测. 将算法应用于聚变堆形变部件检测, 测试结果表明, 本算法在计算效率、处理大规模网格方面都取得了良好的效果.

在进一步的工作中, 该算法将被集成至CFETR集成设计平台, 为支持聚变堆设计提供快速的形变部件碰撞检测功能.