在无线电通信技术中, 由于电磁环境的日益复杂, 信号传输过程中存在着大量自然或者人为干扰信号. 这些干扰信号和目标信号在时域和频率以部分重叠或完全重叠的形式混叠在一起. 随着无线电通信的快速发展和频谱资源的日益紧张, 信号的时频重叠现象已难以避免. 由于接收到的混合信号是在时域和频域重叠的, 常规的时域和频域滤波等技术都无法使用, 这使得信号的干扰抑制变得尤为困难^[1].

目前, 对于复杂电磁环境下的信号和干扰的分离主要集中在单载波重叠信号的分离问题中. 单载波重叠信号的分离主要分为三类: 第一类, 变换域滤波^[2,3], 即先将重叠信号变换到可分离的变换域, 然后通过变换域滤波实现单载波重叠信号的分离, 该类方法仅适用于变换域可分的情况, 在实际中很难找到这类变换域, 并且实现过程复杂. 第二类, 基于贝叶斯估计准则的分离方法^[4–7], 通过计算重叠信号的后验概率来实现信号的分离, 该类方法性能好, 且适用范围广, 但是该类方法需要遍历混合信号的所有可能的样本, 它的计算复杂度高, 不适合高阶混合信号. 第三类, 虚拟多通道变换的分离方法^[8–10], 通过信号的预处理将单路重叠信号分解成虚拟的多路信号, 然后再分离重叠信号, 该类方法目前主要应用于机械故障检测中. 此外, 一些联合的单通道分离算法^[11]也被提了出来, 进一步提高了单载波重叠信号的分离性能.

综上所述, 国内外研究者们对重叠信号的分离确实提出了许多新的方法, 但是这些方法的分离性能还有待改进. 信号稀疏表示是一种新兴的信号处理方法, 目前对基于稀疏表示的时频重叠通信信号的分离研究较少, 特别是对基于稀疏表示的2ASK、2PSK和OFDM等通信信号时频重叠下的分离尚未有人研究. 因此, 本文提出了一种基于信号稀疏表示的时频重叠信号分离与重构方法, 该方法实现时频重叠信号干扰抑制与分离的难点主要是过完备联合字典的构建和联合字典下信号的稀疏分解. 因此, 基于信号的稀疏表示理论^[12,13], 本文分别构造信号和干扰的自适应过完备子字典, 并构建联合字典, 利用信号稀疏分解算法, 实现时频重叠下通信信号和干扰的有效分离.

1 基于K-SVD算法的联合字典构造

信号在过完备字典下稀疏表示的研究主要集中在两个方面: 第一, 如何构造一个信号的过完备字典^[14]; 第二, 如何设计快速有效的稀疏分解算法. 本文提出的基于稀疏表示的干扰抑制和信号重构方法先通过K-SVD算法分别构造信号的过完备子字典, 然后再将子字典进行联合, 构建联合字典, 最后在联合字典上进行稀疏分解, 从而实现时频重叠信号的干扰抑制.

1.1 K-SVD字典学习算法

K-SVD是一种经典的字典学习算法^[15], 依据误差最小原则, 对误差项进行SVD分解, 选择使误差最小的分解项作为更新的字典原子和对应的原子系数, 经过不断的迭代从而得到优化的解.

K-SVD算法的具体实现步骤:

1) 字典初始化: 取待分解信号的部分数据作为训练样本组成初始字典.

2) 稀疏编码: 使用OMP算法近似求解稀疏系数, 即:

${x_i} = \arg \mathop {\min }\limits_x \left\| {{y_i} - {D_{k - 1}}x} \right\|_2^2,\;\;{\rm {s.t.}}\;\;{\left\| x \right\|_0} \leqslant {T_0}$

(1)

得到稀疏表示的系数 ${x_i}$ , 构成稀疏矩阵 ${X_k}$ , 其中 ${T_0}$ 表示稀疏性指标.

3) 逐列进行字典更新, 目标函数为:

$\begin{array}{l}\left\| {Y - DX} \right\|_F^2 = \left\| {Y - \sum\limits_{j = 1}^k {{d_j}X_T^j} } \right\|_F^2\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| {\left( {Y - \sum\limits_{j \ne k} {{d_j}X_T^j} } \right) - {d_k}X_T^k} \right\|_F^2\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| {{E_k} - {d_k}X_T^k} \right\|_F^2\end{array}$

(2)

上式中, $X_T^k$ 为稀疏矩阵 $X$ 的第 $k$ 行, ${d_k}$ 为要更新的第 $k$ 列目标原子, ${E_k}$ 表示除去原子 ${d_k}$ 后在所有样本中产生的误差. 如果直接对约束误差矩阵 ${E_k}$ 进行奇异值分解, 则会导致 $X_T^k$ 不稀疏, 因此对 ${E_k}$ 进行变换, 只保留 ${d_k}$ 和 $X_T^k$ 中非零位置乘积的那些项, 形成 $E_R^k$ , 对 $E_R^k$ 进行SVD分解, 更新 ${d_k}$ 、 $X_R^k$ , 直到满足迭代次数停止. 其中 $E_R^k$ 的SVD分解过程表示为:

$E_R^k = U\Sigma {V^{\rm T}}$

(3)

上式中, $U$ 的第1列作为更新后的字典原子 ${d_k}$ 的值, $\Sigma (1,1)$ 与 $V$ 第1列的乘积作为更新后的稀疏系数 $X_R^k$ 的值.

1.2 联合字典的构造

通过对包含不同特征成分的过完备子字典进行联合构建联合过完备字典^[16–18], 联合过完备字典包含丰富的待分解信号的信息, 复合信号在其上具有更好的稀疏性; 同时由于每个分量信号在各自的过完备字典上均具有稀疏性, 利用稀疏分解算法可实现各个分量信号的分离和重构.

假设复合信号 $y = {y_1} + {y_2}$ , 根据信号 ${y_1}$ 构造具有其特征成分的字典 $\phi = \left\{ {{\phi _i},i \in {\Gamma _1}} \right\},{\Gamma _1} = 1,2, \cdot \cdot \cdot ,l$ , 其中 $l$ 表示字典 $\phi $ 的原子个数. 根据稀疏分解理论可知, ${y_1}$ 在字典 $\phi $ 上具有稀疏性,信号 ${y_2}$ 在字典 $\phi $ 上不具有稀疏性. 同理, 根据信号 ${y_2}$ 构造具有信号 ${y_2}$ 特征成分的字典 $\varphi = \left\{ {{\varphi _j},j \in {\Gamma _2}} \right\},{\Gamma _2} = 1,2, \cdot \cdot \cdot ,k$ , 其中 $k$ 表示字典 $\varphi $ 的原子个数. 信号 ${y_1}$ 在字典 $\varphi $ 上不具有稀疏性, 信号 ${y_2}$ 在字典 $\phi $ 上不具有稀疏性, 即字典 $\phi $ 和 $\varphi $ 之间的相关性较小. 由过完备子字典 $\phi $ 和 $\varphi $ , 构建 $D = \left\{ {\phi ,\varphi } \right\} = \left\{ {{\phi _1},{\phi _2}, \cdots ,{\phi _l},{\varphi _1}},\right.$ $\left.{{\varphi _2}, \cdots ,{\varphi _k}} \right\}$ 的联合过完备字典, 其中 $\phi $ 和 $\varphi $ 称为过完备字典 $D$ 的子字典. 由于字典 $\phi $ 和 $\varphi $ 之间的弱相关性及分量信号在各自字典上的稀疏性, 复合信号在联合过完备字典上具有稀疏性.

联合字典的构建步骤:

1) 复合信号 $y = {y_1} + {y_2}$ , 根据信号 ${y_1}$ 构造具有其特征成分的字典:

$\phi = \left\{ {{\phi _i},i \in {\Gamma _1}} \right\},{\Gamma _1} = 1,2, \cdot \cdot \cdot ,l$

(4)

2) 根据信号 ${y_2}$ 构造具有其特征成分的字典:

$\varphi = \left\{ {{\varphi _j},j \in {\Gamma _2}} \right\},{\Gamma _2} = 1,2, \cdot \cdot \cdot ,k$

(5)

3) 构建联合过完备字典:

$D = \left\{ {\phi ,\varphi } \right\} = \left\{ {{\phi _1},{\phi _2}, \cdot \cdot \cdot ,{\phi _l},{\varphi _1},{\varphi _2}, \cdot \cdot \cdot ,{\varphi _k}} \right\}$

(6)

上式中, $\phi $ 和 $\varphi $ 分别表示信号 ${y_1}$ 和信号 ${y_2}$ 的过完备子字典; $l$ 和 $k$ 分别表示字典 $\phi $ 和 $\varphi $ 的字典原子个数.

2 联合字典下信号的稀疏分解与重构

根据信号稀疏分解理论可知, 信号在过完备字典上的稀疏分解模型可表示为:

${\rm{min}}{\left\| x \right\|_0}\;\;\;{\rm {s.t.}}\;\;y = Dx$

(7)

上式中, $y$ 表示待分解信号, $D$ 表示过完备字典, $x$ 表示稀疏分解系数, ${\left\| x \right\|_0}$ 为稀疏系数 $x$ 中非零元素的个数.

时频重叠信号 $y$ 在联合过完备字典 $D$ 上的分解步骤如下:

(1) 首先从过完备字典中分别选出与待分解信号 $y$ 最为匹配的两个字典原子, 其中一个字典原子为 $\phi = \left\{ {{\phi _i},i = 1,2, \cdot \cdot \cdot ,l} \right\}$ , 另一个最为匹配的字典原子 $\varphi = \left\{ {{\varphi _j},j \in 1,2, \cdot \cdot \cdot ,k} \right\}$ , 且分别满足:

$\left| {\left\langle {{\phi _{i0}},{R_0}} \right\rangle } \right| = \mathop {\sup }\limits_{i \in {\Gamma _1}} \left| {\left\langle {{\phi _i},{R_0}} \right\rangle } \right|$

(8)

$\left| {\left\langle {{\varphi _{j0}},{R_1}} \right\rangle } \right| = \mathop {\sup }\limits_{j \in \Gamma 2} \left| {\left\langle {{\varphi _j},{R_1}} \right\rangle } \right|$

(9)

上式中令 ${R_0} = y,\;{R_1} = {R_0} - \left| {\left\langle {{\phi _{i0}},{R_0}} \right\rangle } \right|{\phi _{i0}}$ , 其中 ${R_0}$ 和 ${R_1}$ 分别表示初始残差信号和第一次迭代后的残差信号.

(2) 由于字典 $\phi $ 根据信号 ${y_1}$ 的特征信息构建, 字典 $\varphi $ 根据信号 ${y_2}$ 的特征信息构建, 故它们求出的最佳原子一定包含各自的主要成分. 通过OMP算法继续迭代可得到重叠信号 $y$ 的稀疏表达式为:

$y = \sum\limits_{i = 0}^{m - 1} {\left\langle {{\phi _i},{R_i}} \right\rangle } {\phi _i} + \sum\limits_{j = 0}^{k - 1} {\left\langle {{\varphi _j},{R_j}} \right\rangle } {\varphi _j}$

(10)

根据式(10)可知, 通过信号的分解系数与相对应的原子的线性组合可以重构原始信号, 恢复原始信号的特征. 利用联合字典中前 $l$ 项原子和与之相应的分解系数进行线性组合可以重构信号分量 ${y_1}$ , 同理, 利用联合字典的后 $k$ 项及相应的分解系数可以重构信号分量 ${y_2}$ , 从而可以实现不同分量信号的分离.

3 仿真分析与实验验证 3.1 仿真信号分析

为了验证本文方法在时频重叠通信信号干扰抑制中的可行性, 首先以2ASK信号和2PSK信号的重叠信号作为待处理信号, 进行计算机仿真, 实现字典学习和稀疏分解; 然后以带干扰的多载波OFDM信号为待处理信号, 进行实验验证; 最后对仿真及实验结果分析, 以证明本文方法在信号干扰抑制中的可行性.

首先选取2ASK、2PSK信号进行时频重叠信号的模拟, 其中采样频率 ${f_s}$ 取1000 Hz; 采样间隔 ${T_s}$ 为0.001 s; 载频 ${f_1}$ 为5 Hz、 ${f_2}$ 为4.5 Hz; 基带信号 $m(t)$ 通过对10 bit的二进制序列采样1000个点来表示.

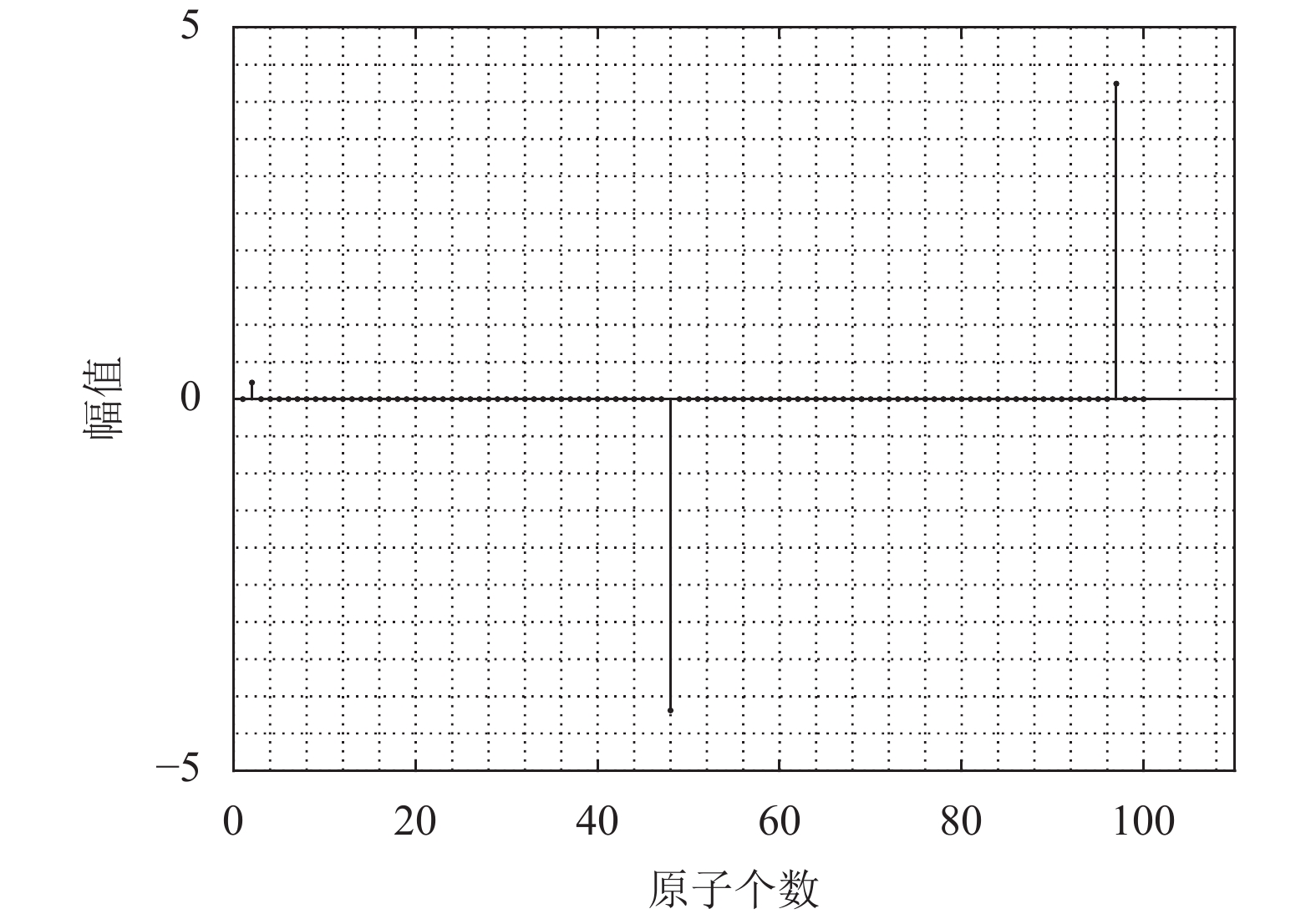
在联合过完备字典下, 通过稀疏分解算法求解得到时频重叠信号的稀疏系数, 如图1所示. 其中联合过完备字典训练的字典原子个数为100个, 2ASK、2PSK各50个. 该时频重叠信号在联合过完备字典下具有稀疏性, 且分解系数中有2个系数远大于零, 其中两个系数的横坐标值一个位于联合字典的前50个原子之中, 另一个位于后50个原子中, 仿真结果与理论分析一致.

以2ASK信号为有用信号, 2PSK信号为干扰信号进行时频重叠, 不同信干比(Signal to Interference Ratio, SIR)下时频重叠信号稀疏分解前后的仿真结果如图2所示.

图2(a)和图2(b)是在SIR=5 dB时时频重叠的2ASK信号和2PSK信号稀疏分解前后的波形图, 图2(a)表示时频重叠的2ASK信号和2PSK信号稀疏分解前的重叠信号波形, 图2(b)表示重叠信号稀疏分解后重构的2ASK有用信号的波形图; 同理, 图2(c)、图2(d)和图2(e)、图2(f)分别是在SIR=10 dB和SIR=15 dB时时频重叠的2ASK信号和2PSK信号稀疏分解前后的波形图. 从图中可以看出, 通过在联合字典上进行稀疏分解, 可以实现有用信号的重构和干扰的抑制, 并且随着信干比的增大, 有用信号重构的效果越来越好.

为了计算2ASK信号和2PSK信号在分解前后的误码率(Bit Error Ratio, BER), 分别取信干比为0 dB、5 dB、10 dB、15 dB、20 dB, 通过对不同信干比下的重叠信号进行分解, 记录并绘制分解前后2ASK信号误码率与信干比的关系图.

信干比与误码率关系曲线如图3所示, 其中BER1表示2ASK非稀疏分解的误码率, BER2表示2ASK信号稀疏分解重构的误码率. 由图3可以看出, 随着输入信噪比的增大, 2ASK信号的误码率降低; 并且稀疏分解重构后2ASK信号的误码率相较与分解前有明显的减小, 因此可以看出本文提出的基于稀疏表示的通信信号干扰抑制与重构方法是可行的.

3.2 OFDM信号分析

为了验证本文方法在时频重叠信号干扰抑制过程中的有效性, 选择多载波OFDM信号进行研究.

下文中字典的训练样本取自YunSDR无线通信硬件平台, 该YunSDR无线通信硬件平台可实现对多载波OFDM信号的自主发送与接收. 其中OFDM数据符号时间为3.2 us, 循环前缀时间为0.8 us, 子载波间隔为312.5 KHz, 子载波数为52, 采用16QAM进行调制. OFDM信号16QAM调制后的星座图如图4.

星座图对于判断调制方式的误码率等有很直观的效用. 在实验中, 从接收的OFDM信号中截取10 000个数据点作为测试样本, 在已训练好的10×600的联合字典上进行稀疏分解和重构. 为了验证本文方法的可行性, 取不同信干比的OFDM接收信号进行稀疏分解和重构, 在信干比SIR=15 dB时, OFDM信号稀疏分解前后的星座图如图5所示.

通过观察图5中的星座图图5(a)和图5(b), 可以很直观的得到OFDM信号在信干比SIR=15 dB下稀疏分解前后的星座图分布情况, 其中分解前比较散乱, 分解去除干扰后星座图分布比较集中. 为了更好的评价文中方法的可行性, 取OFDM信号在不同信干比情况下的误码率来分析, 误码率与信干比的曲线图如图6所示.

由图6可以很直观的看出分解重构后OFDM信号的误码率相较与分解前有明显的下降, 综上可得, 本文提出的基于稀疏表示的通信信号干扰抑制与重构方法是可行的.

4 结论

针对复杂电磁环境下信号与干扰在时频域重叠而难以分离的问题, 本文提出了对时频重叠通信信号构建联合字典稀疏表示去干扰的思想. 与单一成分的过完备字典不同, 联合字典包含更丰富的待分解信号的信息. 首先, 通过理论分析表明, 时频重叠信号在联合过完备字典下能实现有用信号的重构及干扰信号的有效抑制; 然后, 通过对2ASK信号、2PSK信号和OFDM信号在时频重叠情况下, 进行了联合字典的学习和稀疏分解. 仿真与实验结果表明了该方法的有效性, 但是为了得到最优的解, 还需要根据分解信号的特征, 对字典学习过程中的参数做进一步的优化.