计算机系统应用  2018, Vol. 27 Issue (11): 198-204   PDF    
引用本文
康彩红, 王秋萍, 肖燕婷. 基于改进FOA算法的上市公司Z-Score模型财务预警. 计算机系统应用, 2018, 27(11): 198-204.http://www.c-s-a.org.cn/1003-3254/6610.html   
Kang CH, Wang QP, Xiao YT. Z-Score Model Financial Prediction for Listed Companies Based on Improved FOA Algorithm. Computer Systems and Applications, 2018, 27(11): 198-204(in Chinese).http://www.c-s-a.org.cn/1003-3254/6610.html   
基于改进FOA算法的上市公司Z-Score模型财务预警
康彩红, 王秋萍, 肖燕婷     
西安理工大学 理学院, 西安 710054
收稿日期：2018-04-03; 修改日期：2018-04-24; 采用时间：2018-04-27; csa 在线出版时间：2018-10-24
基金项目：国家自然科学基金青年科学资金(11601419)
通讯作者：王秋萍, E-mail: wqp566@sina.com.
摘要：为了提高传统Z-Score财务预警模型的预警能力, 本文将改进FOA算法的良好寻优能力和Z-Score财务预警模型相结合, 提出了一种改进FOA算法的上市公司Z-Score财务预警模型. 采用改进FOA算法来优化Z-Score模型的参数, 降低预测值和目标值之间的均方根误差(RMSE). 经对选取上市公司财务数据的预测值和目标值对比, 且检验其准确率. 实验结果: 传统的Z-Score模型、基本FOA算法优化Z-Score模型和改进FOA算法优化Z-Score模型的预测准确率分别为65%、70%和80%. 实验表明改进的算法较大提升了Z-Score财务预警模型的预测能力, 也表明了该算法的有效性.
关键词: 果蝇优化算法    Z-Score模型    寻优能力    均方根误差    
Z-Score Model Financial Prediction for Listed Companies Based on Improved FOA Algorithm
KANG Cai-Hong, WANG Qiu-Ping, XIAO Yan-Ting     
Faculty of Sciences, Xi’an University of Technology, Xi’an 710054, China
Foundation item: Young Scientists Fund of the National Natural Science Foundation of China (11601419)
Abstract: In order to improve the prediction ability of the traditional Z-Score financial prediction model, this paper proposes a financial prediction model of Z-Score for listed companies based on improved Fruit fly Optimization Algorithm (FOA) by combining the good searching ability of improved FOA algorithm and the Z-Score financial prediction model. The Root Mean Square Error (RMSE) between the predicted value and target value is reduced by improved FOA algorithm being applied to optimize the parameters of Z-Score model. We compare the predicted value and target value of the financial data of listed companies to test the accuracy of financial prediction. The experimental results are as follows: accuracies of the traditional Z-Score financial prediction model, FOA algorithm optimized Z-Score model, and improved FOA algorithm optimized Z-Score model are 65%, 70%, and 80%, respectively. Experiments show that the improved algorithm significantly improves the predictive ability of Z-Score financial prediction model, it is also illustrated the validity of the algorithm.
Key words: Fruit fly Optimization Algorithm (FOA)     Z-Score model     searching ability     root mean squared error    

近年来, 在经济全球化的大背景下, 上市公司所处的经营环境瞬息万变, 使得不少公司正面临着越来越激烈的市场竞争. 因此, 上市公司的财务危机管控和及时监测就显得尤为重要, 不仅能有效准确评估上市公司的财务状况和及时预测其存在的财务风险, 而且可有效帮助上市公司提前预防危机的发生, 增强上市公司化解危机的主动性, 对保护广大投资者和债权人的利益、维护上市公司健康发展和提高公司科学化管理具有重要的现实意义. 财务预警模型包括单变量财务预警模型、条件概率预测模型和多变量财务预警模型等[1,2]. 随着智能优化算法的研究发展, 研究者开始将财务预警模型和智能优化算法相结合, 通过优化模型参数来修正模型, 从而达到理想的预测效果[3,4].

2011年6月台湾学者Wen-Tsao Pan博士受果蝇觅食行为的启发提出了果蝇优化算法(Fruit fly Optimization Algorithm, FOA)[5,6], 然后用FOA来优化多变量预测模型中的传统Z-Score财务预警模型的参数, 虽然优化参数后的预测结果比传统Z-Score财务预警模型好, 但因FOA算法易陷入局部最优、稳定性不强等缺陷, 使得预测结果并不理想.

鉴于此, 本文对基本FOA算法进行改进, 对果蝇寻优步长进行自适应调控, 采用步长缩进的控制策略来避免算法陷入局部最优及提高稳定性等, 提出了基于个体差异的自适应步长果蝇优化算法(Self-Adaptive Fruit fly Optimization Algorithm based on the individual differences, SA-FOA), 然后用于对Z-Score模型参数的优化, 进而提出基于改进FOA算法的上市公司的Z-Score模型. 用修正后的模型分析20家上市公司的财务风险状况[5], 结果表明将改进FOA算法应用于优化Z-Score财务预警模型的参数效果比较显著.

1 Z-Score模型简介

为了有效检验和规避风险, 使公司能够在损失之前及时采取应对措施以及损失达到最小, 保证上市公司的可持续发展, 美国纽约大学教授爱德华·奥特曼(Edward Altman)提出Z-Score财务预警模型[7]. 根据Altman教授长期的实证研究, 选取企业的获利能力、偿还能力、流动性、周转能力和财务杠杆这5个财务指标作为分析变量, 并给这5个指标变量乘以不同权重, 建立Z-Score财务预警模型式(1), 通过Z-Score模型可分析出上市公司的风险概况[8].

$Z = 1.2{X_1} + 1.4{X_2} + 3.3{X_3} + 0.6{X_4} + 1.0{X_5}$ (1)

式(1)中, Z为Z-Score, X1、X2、X3、X4和X5分别代表Altman教授提出的5个不同的财务指标变量. 其中, 这5个Z值模型的指标变量解释见表1.

表 1 Z值模型变量解释 Table 1 The variable explaintion of Z-Score model

Altman教授的Z-Score临界值见表2.

表 2 临界值的说明 Table 2 The statement of critical value

2 果蝇优化算法 2.1 基本果蝇优化算法(FOA)

FOA算法是一种向最优个体不断靠近来实现解空间寻优的新方法. 果蝇觅食的基本原理: ① 嗅觉搜索阶段: 由嗅觉分辨食物气味的来源, 并朝这个方向飞去; ② 视觉定位阶段: 当逼近食物位置附近后, 利用敏锐的视觉来准确判断食物源以及其它同伴聚集的准确位置, 最后飞向食物源. FOA步骤如下[6]:

1)给定果群规模 $sizepop$ , 最大迭代数 $Maxgen$ ; $X\_axis$ 和 $Y\_axis$ 为初始区间内的随机点.

2)对果蝇个体通过嗅觉寻找食物的方向与距离进行赋值:

$\left\{ {\begin{array}{*{20}{c}} {{X_i} = X\_axis + RandomValue} \\ {{Y_i} = Y\_axis + RandomValue} \end{array}} \right.$ (2)

式(2)中, $RandomValue$ 为搜索距离.

3)因无法得知食物源的具体位置, 故需先估计与原点之间的距离 $Dis{t_i}$ , 然后再计算味道浓度判定值Si:

$Dis{t_i} = \sqrt {{X_i^2} + {Y_i^2}} $ (3)
${S_i} = {1 / {Dis{t_i}}}$ (4)

4)将式(4)中计算出的味道浓度判定值Si代入味道浓度判断函数(Fitness function), 此时就可以求得果蝇个体的味道浓度值 $Smel{l_i}$ (即适应值):

$Smel{l_i} = {\rm{function}}({S_i})$ (5)

5)找出果蝇种群中味道浓度最低的一个(求最小值):

$[bestSmell\;\;bestindex] = \min (Smel{l_i})$ (6)

6)记录并保留最优味道浓度判定值 $bestSmell$ 与存储它的X、Y坐标, 这样果蝇就可以利用视觉飞向该位置:

$\left\{ {\begin{array}{*{20}{c}} {Smellbest = bestSmell} \\ {X\_axis = X(bestindex)} \\ {Y\_axis = Y(bestindex)} \end{array}} \right.$ (7)

7) 重复执行步骤2)~ 5), 并与前一代最佳味道浓度值作对比, 是否优于前一代最佳味道浓度值, 且当前迭代数是否小于最大迭代数 $Maxgen$ , 若是, 则执行步骤6); 否则, 结束算法.

2.2 基于FOA的改进果蝇优化算法

当使用基本FOA算法求解各种优化问题时, 在其步骤2)的迭代过程中, 由于给予每个果蝇个体搜寻食物的方向与距离 $RandomValue$ 这一参数赋予的值是随机的, 而影响它的唯一一个因素就是在搜索中采用的固定步长, 再加上算法个体之间的信息交互能力较弱, 从而一定程度上限制了算法的搜索寻优能力. 由此可知, 迭代过程中并未考虑每个果蝇个体当前所处位置优劣的差异性, 如果采用固定的搜索迭代步长, 则限制了果蝇群体的搜索能力, 将会致使果蝇个体中迭代步长较小的个体收敛缓慢, 造成算法早熟而陷入局部极值; 而搜索迭代步长较大的个体则又容易引起迭代后期强烈的振荡以及局部寻优能力的降低. 因此为了得到较理想的优化效果, 在文献[9–13]的基础上, 本文提出了采用基于个体差异的自适应步长果蝇优化算法(Self-Adaptive Fruit fly Optimization Algorithm based on the individual differences, SA-FOA).

SA-FOA算法下步长值主要通过两部分来实现调控, 见式 (8). 首先衰减部分, 这部分根据当前迭代次数变化形成一个指数衰减量; 其次根据每个果蝇个体当前所处位置的差异性, 将前一代果蝇个体位置的味道浓度值和前一代群体最优值同时考虑进去, 这样可使迭代步长值随着果蝇个体当前所处的位置需求进而来实现搜索步长的自适应更新, 通过这两部分的调控关系可使果蝇个体根据自身所处位置情况来选择不同的步长. 由式 (8)可知, 该方式下搜索步长值总体是呈递减趋势, 且位置较差的果蝇个体能获得相对更长的搜索步长值, 使得果蝇群体兼具较强的全局勘探和局部开发能力, 从而增强整个算法的搜索寻优能力.

${C_i} = {C_0}{{\rm{e}}^{ - \tau g}} + \frac{{\left| {Smell(i) - bestSmell} \right|}}{{\delta bestSmell}}$ (8)

式(8)中, ${C_0}$ 为初始步长值; $\tau $ 为衰减常量; $g$ 为当前迭代次数; $Smell(i)$ 是前代果蝇个体的味道浓度判定值; $bestSmell$ 是前代果蝇群体中最优味道浓度判定值; $\delta $ 是正常量.

使果蝇个体的搜索距离 $RandomValue$ 为:

$RandomValu{e_i} = {C_i} (2 \cdot rand() - 1)$ (9)

对果蝇个体通过嗅觉觅食的随机方向与距离公式更新如下:

$\left\{ {\begin{array}{*{20}{c}}{{X_i} = X\_axis + {C_i} (2 \cdot rand() - 1)}\\{{Y_i} = Y\_axis + {C_i} (2 \cdot rand() - 1)}\end{array}} \right.$ (10)

这样, 通过上述改进便可使算法在迭代初期保持一个较大的搜索步长, 果蝇个体可以在大范围内进行粗搜索, 从而更快搜索到全局最优的范围; 而算法到了迭代后期, 随着群体移动步长自适应地减小, 算法便具有更强的局部搜索能力与更快的收敛速度.

2.3 模拟验证

为验证SA-FOA算法的寻优效果, 以Schaffer函数为例做模拟分析, 如式(11):

$\begin{array}{l}\min f({x_1},{x_2}) = \displaystyle\frac{{({{\sin }^2}(\sqrt {x_1^2 + x_2^2} ) - 0.5)}}{{{{(1 + 0.001(x_1^2 + x_2^2))}^2}}} - 0.5\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - 100 \le {x_i} \le 100\;\;\;\;\;i = 1,2\end{array}$ (11)

Schaffer函数的特点是在定义域内存在一个全局最小值点和无限个局部极小值点. 在MATLAB中分别用SA-FOA、PSO和FOA算法测得其曲线收敛如图1所示. 由图1可看出, SA-FOA算法的收敛效果优于PSO和FOA算法, 寻优效果较好.

图 1 Schaffer函数适应度进化曲线 Fig. 1 The iterative process of Schaffer function

3 基于SA-FOA算法优化Z-Score模型

本文利用SA-FOA算法良好的寻优能力, 将Z-Score模型参数与SA-FOA算法中食物的味道浓度值建立一定关系, 通过模仿果蝇觅食行为, 对模型参数进行优化选择. 在保持5个原变量不变的情况下, 将随机生成的SA-FOA优化参数代入式 (12) 中. 以预测值与目标值的均方根误差(Root Mean Squared Error, RMSE)最小为目标, 优化后模型的参数分别记为T1、T2、T3、T4和T5. SA-FOA算法优化Z-Score模型的参数时, 以RMSE为适应度函数如式 (13):

$\hat Z = {T_1}{X_1}{\rm{ + }}{T_2}{X_2}{\rm{ + }}{T_3}{X_3}{\rm{ + }}{T_4}{X_4}{\rm{ + }}{T_5}{X_5}$ (12)
$S{{mel}}{{{l}}_i} = Fitness = RMSE$ (13)

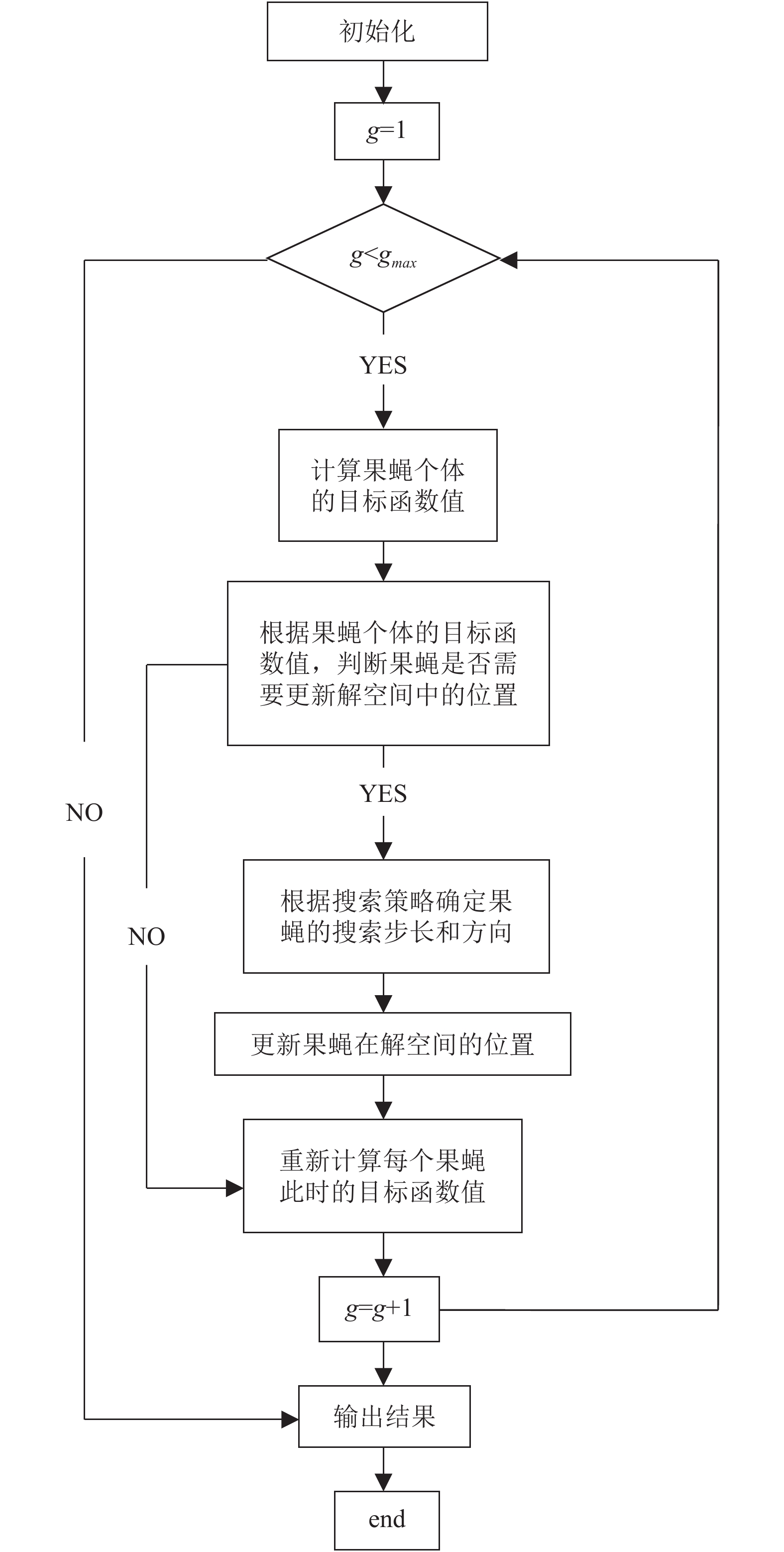
SA-FOA优化Z-Score模型的流程如图2所示.

图 2 SA-FOA优化Z-Score模型流程图 Fig. 2 Flow chart of Z-Score model optimized by SA-FOA

4 实证分析 4.1 实验原理

采用SA-FOA算法和FOA算法优化Z-Score模型参数的实验原理就是: 首先, 将5群果蝇群体进行初始化, 分别指派给参数T1、T2、T3、T4和T5; 然后, 给它们每个群体设定有20只果蝇, 并且将随机初始化果蝇群体的位置区间设置为[0, 1], 进行迭代时, 将果蝇搜寻食物的随机方向和距离区间设置为[–1, 1]; 最后, 通过100次迭代搜寻得到最佳模型的优化参数T1、T2、T3、T4和T5, 这样会使优化后的Z-Score财务预警模型所得到的结果逐渐趋近于目标值Y.

本文以20家上市公司的财务数据作为研究分析对象, 它的财务指标数据见表3. 其中, X1、X2、X3、X4和X5分别表示不同的财务指标变量, Y则表示上市公司的财务状况(0代表危机公司; 1代表正常公司).

测试实验环境为内存8.00 GB, 机器主频3.60 GHz, 操作系统为Windows7, 用Matlab编程在Matlab R2014a实现.

4.2 Z-Score模型的仿真实验

根据传统Z-Score模型对表3中的20家企业进行财务预警仿真实验. 测得这20家上市公司的Z-Score值的测试数据结果见表4, 并将表4结果与表3中的目标值Y进行对比, 发现通过传统的Z-Score财务预警模型来预测上市公司的财务状况时, 有第3、7、8、9、10、12和第17家上市公司的财务状况的预测值不正确, 其预测准确率为65%.

4.2.1 仿真实验与结果分析

根据表4的预测结果, 我们发现传统Z-Score财务预警模型对上市公司的财务危机预警能力并不高, 存在不足. 因此, 传统的Z-Score模型在预测财务危机预警时, 其判定能力有进一步优化和改善的空间.

4.2.2 FOA优化Z-Score模型参数的仿真实验

采用基本FOA算法对表3中的20家企业进行财务预警仿真实验. 算法的参数设置: 果群规模 $sizepop = 20$ , 最大迭代数 $Maxgen = 100$ . 为了便于分析对比, 本文采用参考文献[6]中的方法设置FOA算法优化Z-Score模型的判定临界值, 在FOA算法优化模型参数中0.5对应2.675, 若预测结果高于0.5(亦即高于2.675)为正常公司, 反之则状况不佳. FOA算法优化后的Z-Score值的测试数据结果见表5, 并将表5结果与表3中的目标值Y进行对比, 发现通过FOA算法优化Z-Score模型参数来预测上市公司的财务状况时, 第3、7、8、9、10和12家上市公司的财务状况的预测值不正确, 其预测准确率为70%.

表 3 20家上市公司财务数据 Table 3 Financial data of 20 listed companies

表 4 20家上市公司的Z-Score值 Table 4 The z-score value of 20 listed companies

4.2.3 SA-FOA优化Z-Score模型参数的仿真实验

采用SA-FOA算法对表3中的20家企业进行财务预警仿真实验. 算法的参数设置: 果群规模sizepop=20, 最大迭代数 $Maxgen = 100$ , 初始步长C0=0.2, 衰减常量τ=0.005, 正常量 $\delta $ =2, 判定临界值对比标准同上. 用SA-FOA算法优化Z-Score模型参数来预测上市公司的财务状况时, 从表6可看出, 有第 $3$ 、 $7$ 、 $8$ 和 $9$ 家上市公司的财务状况的预测值不正确, 其预测准确率为80%.

根据表5的预测结果, 我们发现用基本FOA算法优化Z-Score模型参数进行财务预警时, 准确率虽有所改变, 但因FOA算法易陷入局部最优及稳定性不强的问题, 使预测效果还有待提高.

表 5 20家上市公司的FOA优化Z-Score值 Table 5 FOA optimizing Z-Score value of 20 listed companies

由表7 RMSE分析可知, SA-FOA算法优化Z-Score获得的RMSE较小, 表明其预测效果较好.

表 6 20家上市公司的SA-FOA优化Z-Score值 Table 6 SA-FOA optimizing Z-Score value of 20 listed companies

表 7 两种算法优化下的RMSE值对比结果 Table 7 The comparison results of RMSE

从图3基本FOA算法优化Z-Score模型参数和SA-FOA算法优化Z-Score模型参数的RMSE寻优收敛图可知, 随着迭代次数的增加, SA-FOA算法优化Z-Score模型参数的能力优于FOA算法优化Z-Score模型参数的能力, 收敛时对应的迭代次数明显小于基本FOA算法优化Z-Score模型所对应的数值, 且速度较快.

图 3 RMSE收敛图 Fig. 3 The convergrnce of RMSE

综合以上对比分析结果, 表明了采用SA-FOA算法优化后的Z-Score财务预警模型的准确性和高效性. 经SA-FOA算法优化Z-Score模型参数, 当其适应度达到最小值时, 其优化后的Z-Score模型参数T1、T2、T3、T4和T5分别为: 0.3275、0.2907、0.3180、0.2206和0.2337.

5 结论

为了提高传统Z-Score财务预警模型的预警能力, 本文提出了一种基于改进FOA算法的上市公司的Z-Score财务预警模型. 通过对基本FOA算法的移动步长进行改进, 并将其与传统的Z-Score财务预警模型相结合, 用于对Z-Score模型参数的优化和完善. 经仿真实验表明优化后的财务预警模型具有较好的预测效果.

参考文献
[1]
游达明, 刘亚庆. Z值财务预警模型在交通运输业的修正与应用 . 华东经济管理, 2015, 29(7): 9-13. DOI:10.3969/j.issn.1007-5097.2015.07.002
[2]
Ko YC, Fujita H, Li TR. An evidential analysis of Altman Z-score for financial predictions: Case study on solar energy companies . Applied Soft Computing, 2017, 52: 748-759. DOI:10.1016/j.asoc.2016.09.050
[3]
徐金鑫. 基于GA-RBF的上市公司财务预警模型研究[硕士学位论文]. 杭州: 浙江工商大学, 2010.
[4]
周辉仁, 郑丕谔, 王嵩, 等. 基于粒子群优化算法的LS-SVM财务预警. 计算机工程, 2009, 35(10): 280-282. DOI:10.3969/j.issn.1000-3428.2009.10.094
[5]
潘文超. 果蝇最佳化演算法: 最新演化式计算技术. 台中: 沧海书局, 2011.
[6]
Pan WT. A new fruit fly optimization algorithm: Taking the financial distress model as an example. Knowledge-Based Systems, 2012, 26: 69-74. DOI:10.1016/j.knosys.2011.07.001
[7]
Altman EI. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. Journal of Finance, 1968, 23(4): 589-609. DOI:10.1111/j.1540-6261.1968.tb00843.x
[8]
Chen HW, Hu ZB, Ye ZW, et al. Research of P2P traffic identification based on neural network. Proceedings of 2009 International Symposium on Computer Network and Multimedia Technology. Wuhan, China. 2009. 1–4.
[9]
Yin LJ, Li XY, Gao L, et al. A new improved fruit fly optimization algorithm for traveling salesman problem. Proceedings of the Eighth International Conference on Advanced Computational Intelligence. Chiang Mai, Thailand. 2016. 21–28.
[10]
韩俊英, 刘成忠. 自适应调整参数的果蝇优化算法. 计算机工程与应用, 2014, 50(7): 50-55. DOI:10.3778/j.issn.1002-8331.1301-0274
[11]
张宏艺, 洪大华, 崔广健, 等. 改进免疫粒子群算法在矿车调度优化中的应用. 计算机系统应用, 2017, 26(6): 9-16. DOI:10.15888/j.cnki.csa.005817
[12]
Yu Y, Li YC, Li JC, et al. Self-adaptive step fruit fly algorithm optimized support vector regression model for dynamic response prediction of magnetorheological elastomer base isolator. Neurocomputing, 2016, 211: 41-52. DOI:10.1016/j.neucom.2016.02.074
[13]
Li HY, Chen JQ, Huang QZ, et al. An improvement of fruit fly optimization algorithm for solving traveling salesman problems. Proceedings of 2014 IEEE International Conference on Information and Automation. Hailar, China. 2014. 620–623.