引言

在计算机视觉领域, 目标跟踪是一个有趣且有意义的课题. 其在社会中广泛应用于金融, 交通, 人机交互等领域. 从目标跟踪问题提出到现在已经有一段时间了, 大量科研工作者对这一方向进行了不懈的努力研究, 提出了许多优秀的算法. 视频目标跟踪面临的挑战主要有光照变化、尺度变化、目标遮挡等.

近年来, 相关滤波运用到目标跟踪领域取得了相当不错的效果. 2010年Bolme等人在文献[1]中首次将相关滤波方法引入到目标跟踪领域, 提出了最小误差输出平方和(Minimum Output Summer of Squared Error, MOSSE). 作者借助于快速离散傅里叶变换, 运用相关滤波将时域上的卷积转换为频域上的点积, 大大的减少了运算量. 同时论文所提方法跟踪效果也有669帧每秒的出色表现. 由于其在跟踪上面展现出的优秀结果, 此后基于此算法改进算法相继提出, 最具有代表性的是循环结构跟踪(Circulant Structure Kernel, CSK)^[2]方法. 该方法首次在跟踪中提出了密集抽样, 使得训练出来的滤波器更加的鲁棒和精确. 2014年Henriques等人在文献[3]提出核相关滤波跟踪算法(Kernelized Correlation Filter, KCF), 该方法在CSK的基础上用方向梯度直方图(Histogram of Oriented Gradient, HOG)特征代替了原算法中仅仅使用的像素灰度值特征, 从而提高了跟踪的准确性. Danelljan在论文[4]中在CSK的基础上引入了颜色特征(CN), 增强了视频跟踪的鲁棒性, 在速度方面也取得了不错的效果. 对于相关滤波在目标尺度变化不敏感的问题上, Danelljan在DSST^[5]中增加了一个专门用于尺度评估的相关滤波器, 该方法对目标跟踪中尺度变化有较好的处理效果.

本文在核相关滤波(KCF)的基础上提出一种基于遮挡检测的自适应尺度变换相关滤波(OSCF)算法. 本算法在特征提取算法上使用方向梯度直方图(HOG)和原有图像的灰度信息. 针对遮挡问题提出一种基于相关滤波的检测机制. 首先我们将当前帧的目标分为四个小块, 并由此对每一块训练新的分类器. 然后分别计算每一块响应图的PSR值. 然后根据PSR值判断目标的遮挡情况并取得PSR值最大值那一块的峰值响应位置. 最后根据所处中心位置, 提出一种尺度计算策略, 实现尺度自适应更新.

1 核相关滤波(KCF)

本文是以核相关滤波(KCF)为基础架构的. KCF跟踪器以目标为中心, 选取目标及其周围一定范围内矩形图像块x来训练线性分类器, 假设选取补丁图像的尺度大小为M×N. 令M×N等价于 $\beta w \times \beta h$ , 其中 $w \times h$ 为跟踪目标的尺寸, $\beta $ 是目标窗口系数. KCF跟踪考虑所有的循环移位 ${x_{m,n}}$ , $(m,n) \in \left\{ {0, \cdots M - 1} \right\} \times \left\{ {0, \cdots N - 1} \right\}$ ,用来作为分类器的训练样本, 每个样本对应的标签数据 $y(m,n)$ 服从二维高斯分布.

训练分类器的目标是寻找一个函数 $f(x) = $ $ \langle w,\varphi (x)\rangle $ 使得所有的 ${x_{m,n}}$ 和其对应的标签函数平方误差最小, 分类器训练即为:

$w = \arg \mathop {\min }\limits_w \sum\limits_{m,n} {{{\left| {\langle w,\varphi (x) - y(m,n)} \right|}^2}} + \lambda {\left\| w \right\|^2}$

(1)

式中, $\left\langle {\cdot,\cdot} \right\rangle $ 表示內积; $w$ 为分类器的系数; $\phi $ 为核 $\kappa $ 的映射希尔伯特空间, 引入核技巧后, x和 ${x'}$ 的内积可以写成 $\langle \varphi (x),\varphi ({x'})\rangle = \kappa (x,{x'})$ ; $\lambda $ 是一个大于零的常量, 为正则化参数, 其作用是防止函数过拟合.

采用核函数将线性输入问题映射到非线性特征空间 $\varphi (x)$ , 目标函数被最小化为:

$w = \sum\nolimits_{m,n} {\alpha (m,n)\varphi ({x_{m,n}})}, $

(2)

其中, 系数 $\alpha $ 可以定义为:

$F(\alpha ) = \frac{Y}{{{K_x} + \lambda }},$

(3)

在式(3)中F表示傅里叶变换(Discrete Fourier Transform, DFT); Y=F(y); ${K_x} = F({k_x})$ ; $ {k_x}(m,n) = $ $\kappa ({x_{m,n}},x)$ 为核 $\kappa $ 的输出.

KCF跟踪采用的核函数是高斯核函数, 即 $\kappa (x,{x'}) = \exp \left( - \frac{{{{\left| {x - {x'}} \right|}^2}}}{{{\sigma ^2}}}\right)$ . 这里指出向量 $\alpha $ 包含了所有回归系数 $\alpha (m,n)$ .

跟踪过程就是在下一帧中用 $\beta w \times \beta h$ 的窗口来搜索一个图像补丁z, 计算响应值:

$\hat y = {F^{ - 1}}(\hat A \odot {K_{z\hat x}})$

(4)

其中, ${{{F}}^{{\rm{ - }}1}}$ 表示傅里叶变换求逆; $\hat A$ 表示所学得的外观模型系数; $ \odot $ 表示哈达玛积; $\hat x $ 表示学习得到的目标外观模板.

在找到当前帧t的位置后, 整个模型可以一帧一帧的进行更新:

$\left\{ \begin{array}{l}{{\hat x}_t} = (1 - \eta ){{\hat x}_{t - 1}} + \eta {z_t}\\{{\hat A}_t} = (1 - \eta ){{\hat A}_{t - 1}} + \eta {A_t}\end{array} \right.$

(5)

2 遮挡检测

KCF跟踪目标的原理是把当前帧与滤波模板相互作用后得到的响应最大的地方作为目标位置. 其在响应图的响应峰值强度一般使(Peak-to-Sidelobe Ratio, PSR)^[6] 来衡量. PSR的定义为式(6)

$PSR = \frac{{{g_{\max }} - \mu }}{\sigma }$

(6)

式中, ${g_{\max }}$ 表示滤波响应的峰值, $\mu $ 表示响应值旁瓣的平均值, $\sigma $ 表示响应值旁瓣的标准差, 滤波响应值即为式(4)中所得的响应矩阵的元素值.

在跟踪中, 我们令第t–1帧的目标中心位置为 ${p_{t - 1}}$ (第一帧一般由手动设定). 其中假设目标的尺度为 ${w_{t - 1}} \times {h_{t - 1}}$ 像素. 由上文所述, 在第t–1帧中以目标中心点选取尺度大小为 $\beta {w_{t - 1}} \times \beta {h_{t - 1}}$ 像素的图像补丁 ${z_{t - 1}}$ . 不同于文献[3],我们建议对于所有的补丁图进行调整, 然后再使用式(5)对目标的外观 $\hat x $ 和分类系数 $\hat A $ 进行学习更新. 我们令目标中心点 ${p_{t - 1}}$ 坐标为(0, 0), 然后以 ${p_{t - 1}}$ 为中心将 ${z_{t - 1}}$ 平分为四块小的矩形补丁, 同时令它们的中心位置坐标分别为 $({w_1}(t - 1),{h_1}(t - 1))$ ~ $({w_4}(t - 1),{h_4}(t - 1))$ . 将每一块图像块运用式(1)进行新分类器的训练, 所以总共就有4种不同的分类器, 它们的外观模型以及模型系数通过式(5)进行更新.

在第t帧中, 我们在 ${p_{t - 1}}$ 目标的位置选取一个尺度为 $\beta {w_{t - 1}} \times \beta {h_{t - 1}}$ 的候选图像块 ${z_{t0}}$ , 然后通过式(4)计算出最优输出. 在第t帧跟踪目标所在位置 ${p_t}$ 即为响应值最高处. 接着我们在 ${p_t}$ 周围选取一个尺度为 ${w_{t - 1}} \times {h_{t - 1}}$ 像素的图像块 ${z_{t1}}$ , 同时 ${p_t}$ 为中心以建立坐标系统将矩形图像块分为四块. 通过式(4)可以可以求出每一个图像块的置信图 ${y_i}$ , $i \in [1,4]$ , 并通过最高响应点的位置判断图像块的中心位置, 即 $({w_1}(t),{h_1}(t))$ ~ $({w_4}(t),{h_4}(t))$ . 通过式(6)分别可以算出每个图像块的峰值响应强度 $PS{R_i}$ .

本文使用PSR的值作为衡量跟踪目标块和候选图像块的相似程度的一个标准, 同时定义了一个更新权重 ${\delta _i}$ :

${\delta _i} = \left\{ \begin{array}{l}1,PSR \ge \tau \\0,{\text{其他}}\end{array} \right.$

(7)

$\tau $ 为临界阈值, 在图1中可以看到当PSR值低于7.3时, 目标块被严重遮挡, 此时其位置确定是不可靠的.

3 尺度计算

在得到4个分块响应图的最大响应位置后, 计算每个分块的PSR值. 尺度变化率 ${\gamma _t}$ 可以表示为:

${\gamma _t} = \sqrt {\frac{{\left| {{w_i}(t)} \right|}}{{\left| {{w_j}(t - 1)} \right|}}\frac{{\left| {{h_i}(t)} \right|}}{{\left| {{h_j}(t - 1)} \right|}}}, \; \; i,j \in [1,4]$

(8)

其中, $({w_i}(t),{h_i}(t))$ 表示第t帧四块响应图中最大PSR值所在块的最大响应位置 $({w_j}(t - 1),{h_j}(t - 1))$ 这里表示第t–1帧中四块响应图中最大PSR值所在块最大响应位置, 其中对于初始帧用每块的中心位置表示最大响应位置.

第t帧的目标 ${w_t} \times {h_t}$ 可以表示为:

$\left\{ \begin{array}{l}{w_t} = {\gamma _t}{w_{t - 1}}\\{h_t} = {\gamma _t}{h_{t - 1}}\end{array} \right.$

(9)

最终, 在第t帧在以 ${p_t}$ 为中心提取的图像块 ${z_t}$ 的尺度为 $\beta {w_t} \times \beta {h_t}$ . 通过学习得到的外观模型 ${\hat x _t}$ 和学习到的分类系数 ${\hat A _t}$ 可以通过如下式子进行更

$\left\{ \begin{array}{l} {\hat x _t} = (1 - {\delta _i}\eta ){\hat x _{t - 1}} + {\delta _i}\eta {z_t} \\ {\hat A _t} = (1 - {\delta _i}\eta ){\hat A _{t - 1}} + {\delta _i}\eta {A_t} \\ \end{array} \right.$

(10)

4 算法实现

本节对算法实现步骤进行展示, 主要分为参数初始化、目标定位、遮挡检测、尺度计算、模板更新五部分. 算法流程如图2所示.

5 实验结果分析 5.1 评判标准

为了评估本文算法在跟踪目标方面的性能, 本文选取了8段公开的视频, 视频包含了光照变化, 目标遮挡, 尺度变化, 目标旋转等问题. 使用文献[7]中评估标准, 即距离精度(Distance Precision, DP)、成功率(Success Rate, SR)和中心位置误差(Centre Location Error, CLE). 精确度是指跟踪目标的中心坐标与人工标定的准确值间的欧式距离小于某个阈值的帧数占全部视频帧数的百分比, 阈值越低时精确度越高, 则跟踪效果就越好. 成功率是指包围跟踪目标的边框区域与人工标定的准确值间的重叠率大于某个阈值的帧数占全部视频帧数的百分比. 当阈值越高时成功率越高, 则跟踪效果越好.

5.2 参数设定

在PC机上(Windows 10系统, Inter Core i7-6700, 3.40 GHz, 4 G内存)上基于Matlab 2013b完成实验. 对于每一帧图像, 在选取图像块z时扩展系数 $\beta {\rm{ = }}2$ , 图像块z均放缩到128×128像素, 目标大小即为64×64像素, 每个子块的大小为32×32像素; 在分类器训练过程中: 正则化参数 $\lambda = {10^{{\rm{ - }}2}}$ , 核函数选择高斯核函数 $\kappa {\rm{ = }}(x,{x'}) = ( - \frac{{\left| {x - {x'}} \right|}}{{{\sigma ^2}}})$ , $\sigma = 0.2$ ; 模板更新过程中学习率 $\eta {\rm{ = }}0.065$ ; 移动的平均参数T=2; 目标图像标签函数参数 $\theta {\rm{ = }}0.185$ , 子块图像标签函数参数 ${\theta '} = 0.25$ .

5.3 算法对比

为了评估算法的有效性以及对比算法性能, 本文选取了近年来出现的几种高效的跟踪方法DSST, KCF, TLD, CSK. 表1列出了本文所提算法OSCF与其他几种算法的性能对比, 性能指标为中心位置误差, 距离精度, 成功率精度和跟踪的平均速度四个方面. 由表1可以看出, OSCF算法的成功率和距离精度相比其它四中算法都有所提高. 在成功率方面OSCF算法分别提升了1.9%, 30%, 6.7%, 70.1%; 在距离精度方面分别提升了0.4%, 10.8%, 21.5%,71.1%. 所达到的跟踪平均速度为76.8帧/每秒,可以达到实时性的要求.

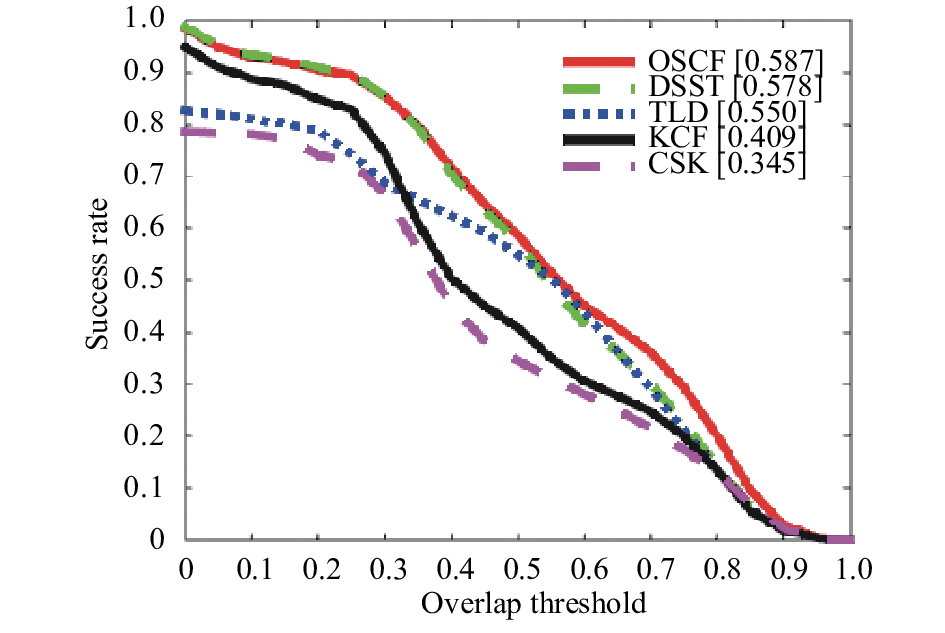
图3和图4分别表示本文算法的距离精度曲线和成功率精度曲线, 图中红色实线表示本文所提算法, 从两图中可以看出本文算法OSCF在目标跟踪方面相较其他算法都要优秀.

图5列举了OSCF, DSST和KCF三种算法在其中八段视频中目标跟踪效果图, 每段视频抽取具有代表性的两帧. 其中视频的共性在于他们都具有尺度变化问题, 另外在视频2和视频8中还含有目标遮挡问题, 视频4中视频还有光照变化问题, 视频5中含有目标旋转问题, 视频6中含有目标快速移动等问题. 图中红色实线表示的是本文所提算法OSCF, 蓝色虚线和绿色虚线分别表示的是DSST算法和KCF算法. 从视频图片帧可以看出, 本文算法OSCF在处理光照变化, 目标旋转, 目标快速运动等问题有效处理的同时, 对目标遮挡和目标尺度变化等问题也达到了较好的跟踪效果, 特别是尺度变换方面算法做到了较好的处理.

6 结语

本文在KCF的基础上引入分块的思想, 提出一种遮挡检测机制, 对分块PSR值的研究分析, 得出目标的遮挡程度, 在此基础上提出一种自适应的尺度处理方法, 在一定程度上解决了相关滤波对于尺度不敏感的问题. 实验仿真结果表明OSCF算法跟踪性能要优于其他算法, 能够实现实时跟踪, 在处理尺度变换的同时, 对于日常跟踪中遇到的遮挡、光照、形变等问题也具有一定的鲁棒性. 同时发现本算法存在的一定的缺陷: (1)当遇到目标快速运动, 大幅度的形变时会出现漂移甚至丢失的问题; (2)当目标漂移或丢失时跟踪无法重新侦测直至视频结束. 下一步研究的方向是, 在研究处理目标尺度的同时也要考虑跟踪的鲁棒性, 做到长时跟踪.