2. 中国科学院大学, 北京 100049
2. (University of Chinese Academy of Sciences, Beijing 100049, China
人口规模的增长和全球气候的不断变化对野生动物的生存环境产生极大的负面影响[1]. 了解动物的潜在栖息地是生态学、自然资源管理和保护的中心主题之一[2]. 物种分布模型利用动物出现的数据并结合出现点所在位置的多种生态位因子, 例如温度、降雨、土壤、斜坡、植被指数等因子, 对物种分布进行建模, 进而预测物种在其它特定地区或者在相同区域不同时间出现的概率值, 概率值的大小反应了物种对该地区环境的偏好程度. 因此物种分布模型可以用来分析物种与环境变量之间的关系, 尤其是气候变化条件下对物种潜在栖息地分布的影响[3], 还有助于研究入侵物种潜在的栖息地扩张范围[4,5]或者濒危物种潜在栖息地的萎缩[6]. 在动物出现数据获取方式上, 传统的方式是通过野外调查、各标本馆的标本数据、各类公开的文献记载等方式获取有用的数据, 这种方式获取的单个物种尤其是稀有物种的有效样本非常少且容易存在误差, 尤其是地理位置精度不高, 例如有些较早记录没有经纬度信息, 只存储所在位置的县名, 甚至是所在的省市. 近年来随着各种先进数据采集设备的广泛应用, 例如Argos, GPS和无线追踪器等, 使得我们可以对单一物种获得大量的有效的动物出现数据, 有利于我们提取更多的有效训练样本从而使用更加复杂的模型对其进行建模和预测.
最大熵模型(MaxEnt)[7]自从提出来以来就被广泛应用来预测各种动植物的潜在分布或者分析入侵物种的适合生长区. Gibson[8]等人利用MaxEnt模型来预测稀有物种鹦鹉在澳大利亚西南部的潜在分布, 通过模型得到鹦鹉喜欢海拔相对较高, 远离河流, 有植被覆盖的地形相对平缓的栖息地. 吴庆明[9]等人利用丹顶鹤2012-2013年营巢分布点和环境特征变量, 通过MaxEnt分析丹顶鹤在扎龙保护区的潜在栖息地分布情况. Hu[3]等人利用MaxEnt对地形, 气候, 生境(土地覆盖)和人为影响这些变量进行建模, 预测濒危候鸟在五个不同地区的潜在越冬栖息地以及在不考虑物种传播的基础上分析将来气候变化对越冬栖息地的影响. MaxEnt模型的最大好处是只需要物种在研究区域明确出现的数据以及出现位置的环境信息就可以有效的进行建模分析, 尤其在小样本集的情况下比其它物种模型取得更好的效果. 近年来随着机器学习应用面的日益扩展, 越来越多的方法利用有/无物种出现数据建立机器学习模型来预测物种分布[6,10–14], 包括人工智能网络(ANN)[12], 分类回归(CART)[13], 随机森林算法[14]等. Yoo[12]等人通过ANN对50个地点收集的13个生态位变量数据进行建模, 预测潮汐滩地的物种多样性. 基于生态位的方法来分析物种的潜在分布主要存在以下三个问题: 1)将原始遥感数据聚合成离散的土地覆盖类型或者植被覆盖指数会导致新的分类误差, 而且在转换过程中大量其它可用的信息可能会丢失以及导致时间粒度和空间分辨率变大. 2)对原始遥感影像进行分类从而获得相应的生态位因子, 这个过程本身就需要花费大量的计算和人力成本. 尽管中尺度的遥感影像是免费公开的, 但是对影像进行分类需要有一定的相关领域知识以及相关的计算过程. 3)传统方法在样本选择上往往局限于少数一些观察点, 在时间跨度和空间范围上都有一定的限制, 适合于栖息地范围分布地比较集中的物种. 斑头雁夏季繁殖在高原湖泊, 越冬则在低地湖泊、河流和沼泽地等, 主要以禾本科和莎草科植物的叶、茎、青草和豆科植物种子等植物性食物为食. 因此影响斑头雁潜在分布的主要因素有植被情况, 湖泊河流分布和温度等. 我们可以从遥感影像中提取植被情况和湖泊河流分布情况, 以及从气象站中获取温度数据, 因此本文直接以遥感图像作为卷积神经网络模型的输入, 避免了传统生态位模型中提取特征的过程, 然后结合温度对斑头雁的出现数据进行建模.
本文首先利用斑头雁的轨迹数据, 结合Landsat遥感影像来获得空间和时间都跨度大的有效训练样本, 从而解决传统数据样本少的问题. 由于斑头雁每年都会在越冬区和繁殖区之间进行来回迁徙, 我们通过DBSCAN聚类算法对轨迹数据进行聚类来发现其在整个年度活动过程中的停留区, 从停留区提取的数据来标记遥感影像数据的正(出现)样本, 避免迁徙飞行过程中的数据产生的干扰, 能更加符合斑头雁的实际栖息地环境; 其次, 设计一种多维卷积神经网络(M-CNN)结构, 利用1-D卷积和2-D卷积操作来分别从温度序列数据和遥感影像图片提取特征从而进行训练并预测斑头雁在青海湖地区的潜在栖息地.
1 基于M-CNN的栖息地预测本文的系统主要分为两步(如图1所示): 1)正/负样本提取, 斑头雁是迁徙物种, 每年都会进行春季和秋季迁徙, 越冬区和夏季活动区距离很远, 相差一两千公里, 导致采集到的原始GPS数据覆盖范围很广(如图2), 直接将所有GPS点所在的位置都划为正样本显然不符合斑头雁实际情况. 2)模型训练和预测.

|
图 1 基于CNN的栖息地预测算法 |
|
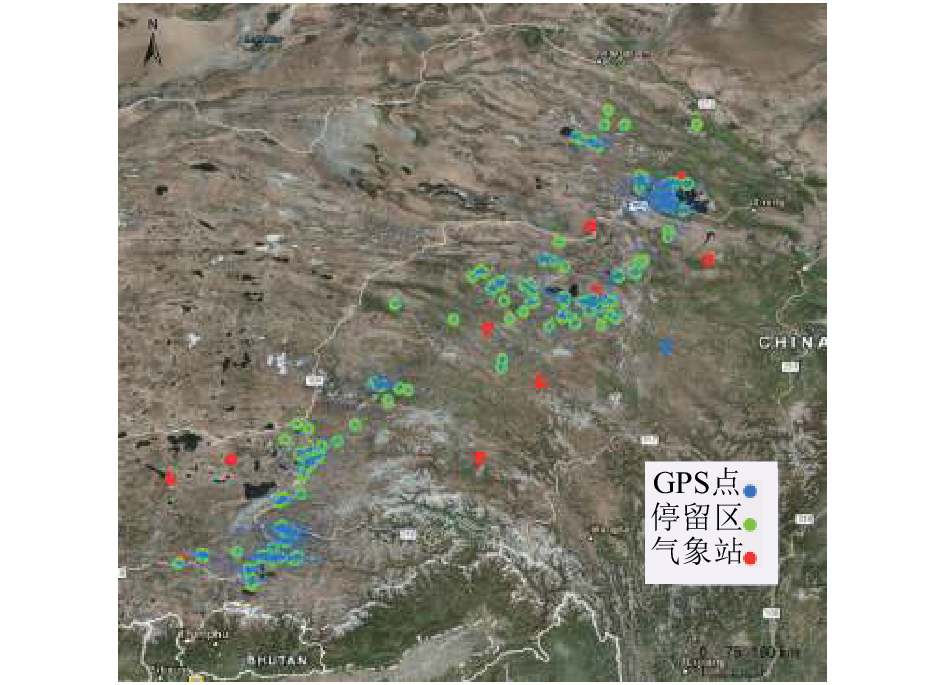
图 2 蓝色点为采集的斑头雁GPS数据点; 绿色点为基于DBSCAN的斑头雁轨迹数据聚类结果, 表示斑头雁的栖息地; 红色为NOOA上离这些栖息地最近的10个气象站. |
1.1 正/负样本提取
DBSCAN[15]是一种典型的基于密度的聚类算法, 它将在给定半径的邻域中包含的点大于给定的最小值的点作为核心点, 通过迭代查找的方法找到各个类簇所包含的所有密度可达的点. 斑头雁的运动轨迹无法连续记录下来, 而是由一系列离散的采样点组成,
| 表 1 lon和lat表示经纬度, animal表示采集的动物的编号, time采集时间 |
1.2 M-CNN网络结构
CNN是一种主要由卷积层、池化层、全连接层和激活函数组成的多层深度神经网络模型, 采用卷积核共享参数, 减少了训练的参数. 图3为本文的M-CNN网络结构. 2-D卷积的输入数据为6通道的16×16像素块大小的Landsat 5 TM影像和1-D的卷积输入为15×3大小的温度序列数据, 随后图片数据通过三层卷积, 两层最大池化层, 温度数据经过两层卷积层, 然后将两个卷积过程获得的特征拼接起来输出到两层全连接层和两层Dropout层, 最后输出到softmax分类器. 卷积神经网络的第一层卷积层的滤波器主要用来检测低阶特征, 比如边、角、曲线等, 越往后的卷积层检测更高阶的特征. 我们在第一层分别使用多个不同尺寸的卷积核, 以获得不同尺度的特征, 再把这些特征结合起来作为第一层卷积层的输出来以获得更好的低阶特征. 为了减少训练过程中的内部协变量偏移(internal covariate shift), 我们在执行激活函数前加入了批量规范化(batch normalization)操作[16], 使得输出的各个维度的均值为0, 方差为1, 这也有助于提高模型的收敛速度和减少对Dropout的要求.
卷积层可以看成是输入图像/前一层特征图与一个可训练的卷积核进行卷积运算得到的结果, 例如第一个1×1的卷积成可以用如下表示:
| $a_{ij}^k = \sum\limits_{c = 1}^7 {(a_{ij}^c*K_{ij}^c)} $ |
其中,
批量规范化操作如果将前一层的数据做规范化后直接进入下一层会改变前一层网络所学到的特征, 因此作者引入了一对可学习参数γ和β, 使得整个批量规范操作如下[16]:
| ${\mu _B} \leftarrow \frac{1}{m}\sum\limits_{i = 1}^m {{x_i}} $ |
| $\sigma _B^2 \leftarrow \frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - {\mu _B})}^2}} $ |
| $\widetilde {{x_i}} \leftarrow \frac{{{x_i} - {\mu _B}}}{{\sqrt {\sigma _B^2 + \varepsilon } }}$ |
其中, m为批量训练样本的大小, ε是加入的噪声.

|
图 3 栖息地预测系统的M-CNN网络结构, 其中Conv为卷积层, BN表示Batch Normalization, FC为全连接层 |
池化层经常在卷积层后面, 能够对卷积所输出的图像特征进行聚合统计. 将上一层输出的卷积特征划分到若干个不重叠的大小为m×n的区域上, 最大池化就是用这m×n个位置上的最大值作为池化后的卷积特征而舍弃其它位置的值. 这样CNN不关注池化窗口内到底是在哪一个位置匹配上了, 只关心是不是有匹配上. 池化层在一定程度上还能降低网络的复杂度, 减少计算量和降低过拟合.
Dropout指在每次批量训练模型时以一定的概率随机让网络中某些隐含层节点的权重暂时不工作, 在下一轮训练时这些神经元又会恢复, 然后再次以一定的概率随机选择部分神经元暂时不工作. 由于每次输入的批量样本进行权值更新时, 隐含节点都是以一定概率随机出现, 从而使得权值的更新不再依赖于有固定关系隐含节点的共同作用, 相当于网络结构在每次训练过程中都发生变化, 避免了对某一局部特征的过拟合.
2 实验和分析 2.1 实验数据本文实验数据来主要来自青海湖地区的29只斑头雁, 它们从2007年到2010年的在青海湖区域和错愕湖区域之间来回迁徙, 每只斑头雁携带有一个便携式遥感设备, 能够通过Argos卫星和GPS接收器进行定位和发送数据, 采集间隔时间设为2小时, 采集数据的存储格式如表1所示, 总共采集到60 161个GPS点(如图2蓝色的点). 斑头雁的栖息地主要分布在从青海湖地区到斑头雁越冬区沿途经过的地方, 通过DBSCAN聚类结果(如图2)我们可以看到主要包括哈拉湖, 青海湖, 冬给措纳湖, 扎陵湖, 鄂陵湖, 曲麻莱县, 隆宝滩自然保护区, 扎木措湿地, 纳木错湖, 羊卓雍错, 拉萨河, 雅鲁藏布江等区域, 其中青海湖和扎鄂陵陵湖是主要的繁殖区和换羽区, 羊卓雍错, 拉萨河, 雅鲁藏布江是主要的越冬区.
本文使用的Landsat 5 TM的遥感影像从USGS(https://earthexplorer.usgs.gov/)官网下载. 我们下载所有研究区域内从2007年到2009年的遥感影像, 通过分析其自带的元数据文件, 移除云层覆盖率大于20%或者影像时间前后十天内没有出现过斑头雁的遥感影像, 剩下的影像用来提取训练数据, 然后下载2010年8月和2011年2月青海湖及其周围区域的4幅云层覆盖率小于20%的遥感影像. 每幅遥感影像有7个波段, 我们使用其中的B1, B2, B3, B4, B5和B7六个波段的值, 每个像素点的分辨率为30 m, 我们样本的大小为16×16×6, 对应的分辨率为480 m, 基本上和GPS设备定位的最大误差相接近. 本文使用了从青海湖到西藏越冬区沿途的10个包含有2007年到2010年温度数据的气象站(如图2所示), 所有温度数据从NOOA(http://gis.ncdc.noaa.gov)网站上下载, 每个气象站每天都保存最高温度、最低温度和平均温度. 针对每幅遥感影像, 我们将离它最近的气象站的当前遥感影像时间的前后7天(包括遥感影像当天, 共15天)的平均温度、最低温度和最高温度作为遥感影像的温度特征.
经过2.1部分的正/负样本提取后, 我们总共得到26 023张16×16×6大小的图片, 其中正样本8696张, 负样本17 327张. 为了使正负样本的数量更加平衡, 我们对每张正样本分别进行左旋转90度和又旋转90度的数据, 并随机抽取2000张加入样本集中, 并按9:1比例分成训练样本和测试样本. 因此, 最后我们共得到28 023张图片, 正样本10 696张, 负样本17 327张, 对应的训练样本和测试样本分别是25 221张和2802张.
2.2 模型训练卷积神经网络的训练主要采用梯度下降法, 包括批量梯度下降(BGD)、随机梯度下降(SGD)和小批量梯度下降(MGD). 其中, 批量梯度下降法每次迭代需要所有样本参与运算, 能够寻找到全局最优解, 但是收敛速度比较慢. 随机梯度下降法则每次迭代利用一个样本来更新参数, 计算成本低, 收敛速度快, 缺点是单个样本可能会带来很多噪声, 使得每次更新不一定朝着全局最优的方向, 容易造成收敛到局部最优解.
本文采用的小批量梯度下降法可以看成是前两种方法的一种折中, 每次迭代计算一小批样本的梯度来更新参数的权值, 这样能够在尽可能寻找到全局最优解的同时加快模型的收敛速度. 为了防止过拟合, 利用L2正则化对网络参数进行约束, 并在全连接层的训练过程中引入了Dropout策略, 即每次迭代中随机放弃一部分训练好的参数[17]. 在模型训练初期, 可以使用较大的学习率来加速收敛, 当训练集的损失下降到一定程度后就不再下降, 容易在一个局部范围内震荡. 为了解决这个问题, 我们采用学习率衰减的方法, 学习率随着训练的进行逐渐衰减. 整个模型的训练参数如表2所示.
| 表 2 CNN模型训练参数 |
2.3 实验设置
我们设置了两组实验, 每组实验都和传统的两个方法进行对比: 基于灰度共生矩阵的特征提取的SVM分类(GLCM+SVM)和本文采用的网络结构中去掉1-D卷积部分的CNN网络(CNN).
对于GLCM+SVM模型, 我们将图片的灰度级别设为64, 每个点选取8组不同的偏移量来计算灰度共生矩阵. 由于灰度共生矩阵的数据量较大, 一般不直接作为区分纹理的特征, 本文选取常见的基于灰度共生矩阵计算出来的统计量来作为SVM模型的输入特征, 包括均值、相关性、对比度、能量、均匀性和最大相关系数等.
第一组实验, 我们分别训练各个模型, 然后利用二分类常见的三个指标: 总体准确率、F1值和曲线下面积(Area Under the Curve of ROC, AUC)[3]来评价各个模型的性能. 在第二个实验中, 我们利用训练好的模型来预测青海湖周围斑头雁潜在的栖息地情况. 青海湖夏天是斑头雁重要的繁殖地, 而冬天都往南迁徙, 很少有斑头雁停留[13], 因此我们分别选取夏季(8月)和冬季(2月)两个不同时期的遥感影像来分析各个模型的预测结果.
2.3 实验结果本文实验环境为12核Intel(R) Xeon(R) CPU E5-2620, 无GPU, 内存64 GB, 编程语言python2.7, 采用Tensorflow-0.9.0深度学习框架[18]进行CNN神经网络训练学习. 表3显示了各个模型在训练数据集上的结果, 可以看出我们设计的网络结构在各个指标上都取得比较好的成绩. 和卷积神经网络相比, 传统的GLCM+SVM在提取特征上没有优势.
| 表 3 3个模型在训练数据集上的分类结果 |
我们选取2010年8月份和2011年2月份的青海湖及其周围的遥感影像进行预测, 预测的斑头雁潜在栖息地分布如图4所示. 对于8月份(图4第一列)的预测结果, GLCM+SVM模型在沿湖区域基本上没有概率特别高的区域, 预测的潜在分布都是在湖面上; CNN和M-CNN模型都会将沿着湖边的部分或者大部分区域标记为概率非常高的区域, 标记面积M-CNN模型会略大于CNN模型; 各个模型在湖面的处理表现差异比较大, 基本上都将湖面标记为潜在分布区, 其中CNN模型会将部分标记为低概率(颜色更深), 其它两个模型基本都是标记为高概率. 8月份, 在青海湖地区对于繁殖成功的斑头雁主要活动是带领幼鸟觅食, 其它斑头雁则进行换羽或者在储备食物做秋季迁徙前的准备. 这些任务都要求斑头雁在食物更丰富、外界因素干扰更小的河口和支流湿地去活动, 这些地方都在离湖面一段距离的地方. 因此M-CNN模型将青海湖离湖较近及其离湖面一段距离内的地方都标记为高概率区域, 更加符合实际情况.

|
图 4 从上到下三行分别是GLCM+SVM、CNN和M-CNN模型; 第一列是2010年8月份的预测结果, 第二列是2011年2月的预测结果. 很低、低、高、很高表示斑头雁出现的概率, 其中很低用透明色表示, 即显示背景. |
2月份斑头雁基本上还在西藏或者其它越冬区, 或者在往青海湖迁徙的前期, 青海湖上还基本上没有适合斑头雁的地方. 从图4第2列中可以看出来三个模型都错误的将少部分区域标记为潜在分布区, 错误标记的面积大小GLCM+SVM>CNN>M-CNN, 也可以看出我们模型准确度更高.
3 结论与展望本文利用斑头雁的轨迹数据, 结合Landsat遥感影像, 提出一种基于M-CNN模型的候鸟栖息地预测方法, 利用1-D卷积和2-D卷积分别从温度序列和遥感影像中提取特征. 有别于传统的方法从遥感影像中计算生态位值作为分类器的特征, 卷积神经网络能够自动从图片中进行学习, 直接处理原始遥感影像来实现对斑头雁潜在栖息地的预测. 基于生态位因子模型一般都是研究大范围区域内适合某个物种的区域分布, 基于遥感影像建模能够比它提供更高空间分辨率和更细时间粒度的潜在分布结果, 有助于更好的了解物种的分布和更好的进行保护. 由于遥感影像数据容易受到云层的影响, 当研究区域被云覆盖住时, 就无法提取有效数据, 而遥感影像周期又比较长, 因此如何减少云覆盖的影响是今后研究的重点.
| [1] |
McKee JK, Sciulli PW, Fooce CD, et al. Forecasting global biodiversity threats associated with human population growth. Biological Conservation, 2003, 115(1): 161-164. |
| [2] |
Nielsen SE, Johnson CJ, Heard DC, et al. Can models of presence‐absence be used to scale abundance? Two case studies considering extremes in life history. Ecography, 2005, 28(2): 197-208. |
| [3] |
Hu JH, Hu HJ, Jiang ZG. The impacts of climate change on the wintering distribution of an endangered migratory bird. Oecologia, 2010, 164(2): 555-565. |
| [4] |
张颖, 李君, 林蔚, 等. 基于最大熵生态位元模型的入侵杂草春飞蓬在中国潜在分布区的预测. 应用生态学报, 2011, 22(11): 2970-2976. |
| [5] |
Bisrat SA, White MA, Beard KH, et al. Predicting the distribution potential of an invasive frog using remotely sensed data in Hawaii. Diversity and Distributions, 2012, 18(7): 648-660. |
| [6] |
Parviainen M, Zimmermann NE, Heikkinen RK, et al. Using unclassified continuous remote sensing data to improve distribution models of red-listed plant species. Biodiversity and Conservation, 2013, 22(8): 1731-1754. |
| [7] |
Phillips SJ, Dudík M, Schapire RE. A maximum entropy approach to species distribution modeling. Proceedings of the 21st International Conference on Machine Learning. Banff, Alberta, Canada. 2004, doi: 10.1145/1015330.1015412.
|
| [8] |
Gibson L, Barrett B, Burbidge A. Burbidge A. Dealing with uncertain absences in habitat modelling: A case study of a rare ground-dwelling parrot. Diversity and Distributions, 2007, 13(6): 704-713. |
| [9] |
吴庆明, 王磊, 朱瑞萍, 等. 基于MAXENT模型的丹顶鹤营巢生境适宜性分析——以扎龙保护区为例. 生态学报, 2016, 36(12): 3758-3764. |
| [10] |
Franco AMA, Brito JC, Almeida J. Modelling habitat selection of Common Cranes Grus grus wintering in Portugal using multiple logistic regression. IBIS, 2010, 142(3): 351-358. DOI:10.1111/j.1474-919X.2000.tb04430.x |
| [11] |
Ball LC, Doherty Jr PF, McDonald MW. An occupancy modeling approach to evaluating a palm springs ground squirrel habitat model. The Journal of Wildlife Management, 2005, 69(3): 894-904. DOI:10.2193/0022-541X(2005)069[0894:AOMATE]2.0.CO;2 |
| [12] |
Yoo JW, Lee YW, Lee CG, et al. Effective prediction of biodiversity in tidal flat habitats using an artificial neural network. Marine Environmental Research, 2013, 83: 1–9.
|
| [13] |
Pittman SJ, Christensen JD, Caldow C, et al. Predictive mapping of fish species richness across shallow-water seascapes in the Caribbean. Ecological Modelling, 2007, 204(1-2): 9-21. |
| [14] |
Rodriguez-Galiano VF, Chica-Olmo M, Chica-Rivas M. Predictive modelling of gold potential with the integration of multisource information based on random forest: A case study on the Rodalquilar area, Southern Spain. International Journal of Geographical Information Science, 2014, 28(7): 1336-1354. |
| [15] |
Ester M, Kriegel HP, Sander J, et al. A density-based algorithm for discovering clusters a density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Portland, OR, USA. 1996. 226–231.
|
| [16] |
Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv: 1502.03167, 2015.
|
| [17] |
Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 2014, 15(1): 1929-1958. |
| [18] |
Abadi M, Agarwal A, Barham P, et al. TensorFlow: Large-scale machine learning on heterogeneous distributed systems. arXiv: 1603.04467, 2016.
|
 2018, Vol. 27
2018, Vol. 27



