2. 中国科学院 声学研究所 中国科学院水下航行器信息技术重点实验室, 北京 100190;
3. 中国科学院大学, 北京 100049
2. CAS Key laboratory of Technology for Autonomous Underwater Vehicles, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
自20世纪80年代开始, 启发式算法得以迅速发展, 较为经典的有遗传算法(Genetic Algorithm, GA)[1], 粒子群算法(Particle Swarm Optimization, PSO)[2], 蚁群算法(Ant Colony Optimization, ACO)[3], 模拟退火算法(Simulated Annealing, SA)[4]等, 并得到了广泛应用. 近些年来, 很多模拟自然界群体行为的新型启发式算法蜂拥而出, 如蝙蝠算法(Bat Algorithm, BA)[5], 萤火虫算法(Firefly Algorithm, FA)[6], 布谷鸟搜索算法(Cuckoo Search, CS)[7]等. 灰狼优化算法(Grey Wolf Optimizor, GWO)是一种2014年由学者S Mirhalili等人提出的新型启发式算法[8], 源于对灰狼群体追踪、围捕、攻击猎物捕食行为的模拟. GWO算法实现简单且具有较强的寻优性能, 因此在各个领域都得到了广泛的应用, 如流水车间调度[9], 医学影像优化[10], 电力系统稳定器的参数优化[11], 多层感知器的训练[12]等.
尽管GWO算法在很多领域获得较成功的应用, 但GWO算法也同其他启发式算法一样, 存在求解精度较低, 容易陷入局部最优等问题. 为提高GWO算法的寻优性能, 国内外学者相继做了很多研究, 改进的方法有几类[13], 一类是对GWO算法种群进行优化, 如引入反向学习理论、混沌扰动理论等优化搜索种群[14–16]; 一类是对GWO算法本身的变量参数进行改进, 如改进收敛因子和种群更新策略等[17]; 还有引入其他进化算法的理论到GWO算法中, 以改进算法寻优新能, 如混合差分进化算法、粒子群算法等[18–20].
为提高基本GWO算法的收敛速度, 获得更高的求解精度, 本文提出了一种基于模糊控制的权重决策灰狼优化算法(Fuzzy Weight Grey Wolf Optimizer, FWGWO). 首先, 提出了一种新的收敛因子, 通过增加前期广度搜索的比例, 可提高算法的全局搜索能力, 同时使算法后期具有更快的收敛速度. 其次, 提出一种基于模糊控制的权重决策策略, 在算法迭代的不同时期. 对决策层的个体赋予不同权重进行决策, 以增强决策的公平性, 提高算法的寻优能力. 最后, 对23个标准测试函数的实验结果表明, FWGWO算法相较于对比算法具有更快的收敛速度和更高的收敛精度.
1 GWO算法 1.1 灰狼群体的社会层级制度社会层级制度是灰狼群体的显著的特征之一, 一般呈金字塔形, 将灰狼群体分为四层, 分别是α, β, δ和ω层, 如图 1所示. 第一层为种群的头狼α, 作为灰狼群体的领导者, 是灰狼群体行为的主要决策者; 处于第二层的是β, 主要负责协助头狼α对狼群的行为做决策, 是头狼的主要候选者; 处于第三层级的是δ, 是灰狼群体比较特殊的一类, 包括侦查员、看护者、狩猎者等; 最底层为ω狼, 负责平衡灰狼群体内部的关系.
1.2 GWO算法描述对于灰狼群体来说, 捕食行为是其另外一个有趣的行为特征. Muro C指出[21], 狼群捕食一般包括以下阶段:
第一阶段: 跟踪、追赶、靠近猎物
第二阶段: 包围, 扰乱猎物, 直到猎物停止移动
第三阶段: 攻击猎物
GWO算法是模拟灰狼群体捕食过程的寻优算法. 寻找最优解的过程可看做狼群捕食的过程, 目标猎物的位置即为对应函数的最优解. 将靠近目标最优解的个体看作狼群中起领导决策作用的狼, 领导个体通过不断更新与目标之间的距离判断移动的方向, 最后带领群体靠近目标.

|
图 1 灰狼群体社会等级示意图 |
为便于利用GWO算法求解函数最优解的问题, 首先对GWO算法进行建模[16]: 定义灰狼种群中最优个体为α, 可理解为种群中适应度最高, 离最优解距离最近的个体, 适应度值排名第二和第三的个体记为β和δ, 剩余个体记为ω.
定义1. 灰狼群体与目标猎物的相对距离. 捕食初期, 狼群会先对猎物进行包围, 狼群个体与猎物之间的相对距离由D表示:
| $D=|C \cdot {X_p}(t) - X(t)|$ | (1) |
| $C=2 \cdot {r_1}$ | (2) |
其中, Xp(t)代表猎物当前的位置, X(t)代表第t代灰狼个体的位置, C为影响因子, r1为[0,1]区间均匀分布的随机数.
定义2. 灰狼个体位置更新. 灰狼个体会根据自己与猎物的相对距离做出位置更新, 下一步灰狼个体的位置为:
| $X(t + 1)={X_p}(t) - A \cdot D$ | (3) |
| $A=2a \cdot {r_2} - a$ | (4) |
| $a=2 - \frac{2}{{Max\_iter}}t$ | (5) |
其中, A为收敛影响因子,
定义3. 灰狼群体位置更新. 在灰狼群体中, α, β和δ三头狼为距离猎物相对最近的狼, 假设这三头狼对猎物的位置具有更多的信息, 因此在捕食过程中由这三头狼带领狼群其他狼一起向猎物靠近, 其他狼每一步移动的位置由这三头狼共同决策. α, β和δ需通过式(6)–(8)分别计算各自与猎物的位置, 然后通过式(9)–(11)更新各自下一步的位置, 则灰狼群体其他狼下一步移动的位置由式(12)决定.
| ${D_\alpha }=|{C_1} \cdot {X_\alpha } - {{X}}|$ | (6) |
| ${D_\beta }=|{C_2} \cdot {X_\beta } - {{X}}|$ | (7) |
| ${D_\delta }=|{C_3} \cdot {X_\delta } - {{X}}|$ | (8) |
| ${X_1}{\rm{ = }}{X_\alpha } - A \cdot {D_\alpha }$ | (9) |
| ${X_2}{\rm{ = }}{X_\beta } - A \cdot {D_\beta }$ | (10) |
| ${X_3}{\rm{ = }}{X_\delta } - A \cdot {D_\delta }$ | (11) |
| $X(t + 1)=\frac{{{X_1} + {X_2} + {X_3}}}{3}$ | (12) |
对于启发式算法, 寻优的过程都涵盖了广度搜索和深度搜索两类操作. 一般, 前期缺少先验知识, 种群会在全局范围内进行搜索, 此时主要为广度搜索, 目的是尽可能探索更广度的区域, 发现较多的全局最优解; 深度搜索则主要是在算法后期, 在广度搜索基础上进行深度开发, 此阶段种群会根据前期搜索的先验知识, 逐渐靠近较优解, 尽可能靠近最优解以及获得更好的求解精度. 一个优秀的寻优算法不仅要求算法有较快的收敛速度, 还要求在前期有较强的探索能力, 在后期有较强的开发能力, 以获得更高的求解精度. 因此, 提高算法的寻优性能务必要协调好广度搜索和深度搜索的比例关系.
在GWO算法中, 变量A是主要影响到广度搜索和深度搜索的变量. 在GWO算法中定义了, 当|A|>1时, 灰狼群体将扩大包围圈, 此时, 算法为广度搜索, 当|A|<1时, 灰狼群体将缩小包围圈, 以完成对猎物的包围攻击, 此时, 算法为深度搜索, 如图 2所示[8].
由式(4)可知, A的变化区间主要由收敛因子

|
图 2 变量A与种群搜索的关系 |
在原GWO算法中, 广度搜索和深度搜索比例为1:1. 为加快GWO算法的收敛速度, 避免原GWO算法容易陷入局部最优的问题, 本文提出了一种新的非线性收敛因子, 增加了前期广度搜索的比例, 一方面利于搜索更多的全局最优点, 避免陷入局部最优, 另一方面该收敛因子在算法后期的取值变化迅速, 能使得算法在后期获得更快的收敛速度, 从而获得更好的求解精度. 改进后的收敛因子由式(13)表示.
| $a=2\sqrt {1 - {{\left( {\frac{t}{{Max\_iter}}} \right)}^2}} $ | (13) |
在GWO算法中, 由式(8)可知, 种群下一次移动的位置由α, β, δ共同做决策, 且决策平均. 显然, 这种平均决策方法并没有考虑α, β, δ的个体特征, 没办法体现出α狼作为主要领导者和适应度最高的个体在决策时的重要性.
为实现自适应调整决策个体在不同时期的权重比例, 本文提出了一种基于模糊控制的权重决策种群位置更新策略, 在算法迭代的不同时期, 通过模糊控制器对α, β和δ赋予不同的权重比例, 使得种群更新的位置更加可靠, 改进的种群更新位置公式如式(14)所示.
| $\begin{aligned} X(t + 1)= & \frac{{f{w_\alpha }}}{{f{w_\alpha } + f{w_\beta } + f{w_\delta }}}{X_1} + \frac{{f{w_\beta }}}{{f{w_\alpha } + f{w_\beta } + f{w_\delta }}}{X_2} \\ & + \frac{{f{w_\delta }}}{{f{w_\alpha } + f{w_\beta } + f{w_\delta }}}{X_3} \\ \end{aligned} $ | (14) |
其中,
基本的模糊控制器一般包括输入量模糊化, 模糊逻辑和模糊判决, 其结构如图 3表示[22].

|
图 3 基本模糊控制器 |
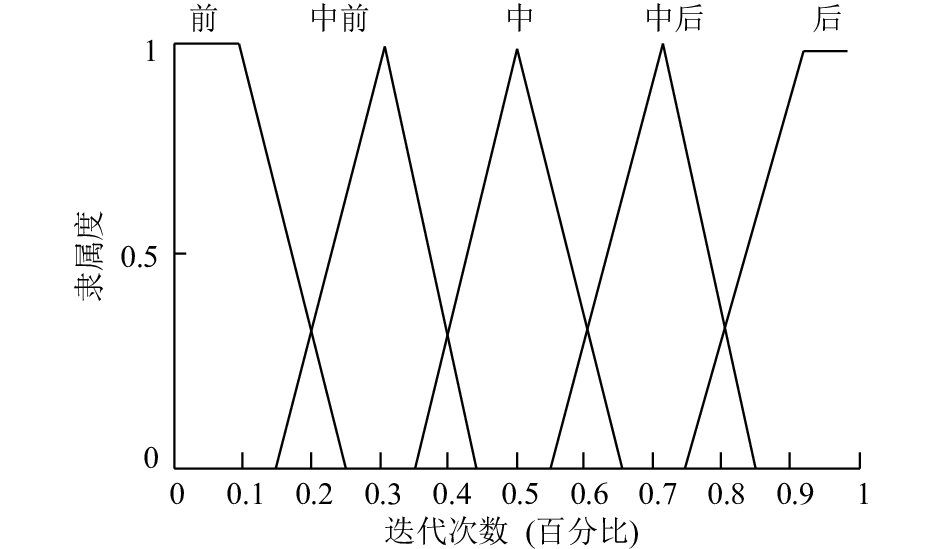
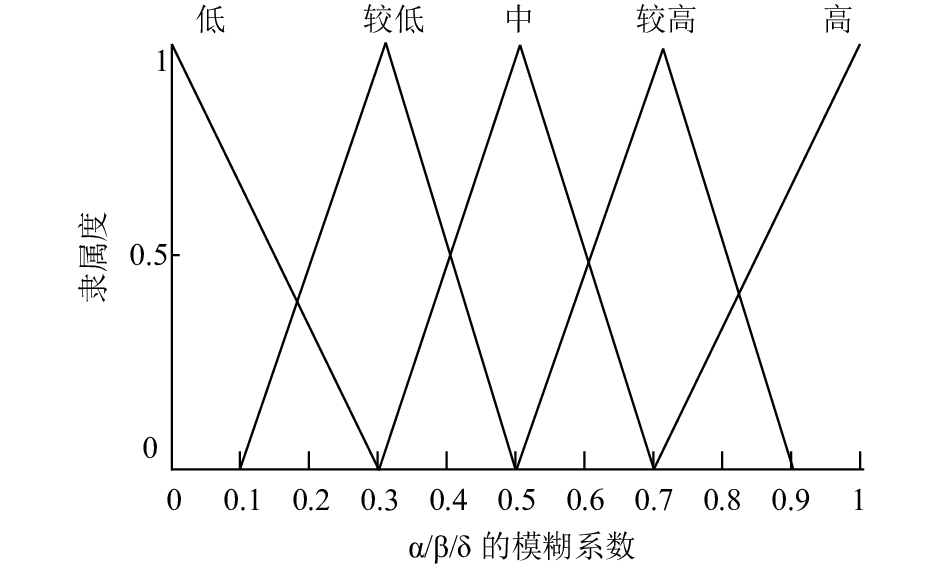
本文定义的模糊控制器包括一个输入和三个输出, 其中迭代次数作为输入, 模糊集包括“前”, “中前”, “中”, “中后”, “后”; α, β, δ的模糊系数作为输出, 模糊集均用“低”, “较低”, “中”, “较高”, “高”来描述. 算法迭代次数的隶属度函数, 如图 4所示, α, β, δ的模糊系数的隶属度函数相同, 如图 5所示.
|
图 4 模糊控制器输入—迭代次数的隶属度函数 |
|
图 5 模糊控制器输出—fwα/fwβ/fwδ的隶属度函数 |
定义如下IF-THEN模糊规则:
规则1. IF<迭代次数为“前”>, THEN<α的模糊系数
规则2. IF<迭代次数为“中前”>, THEN<α的模糊系数
规则3. IF<迭代次数为“中”>, THEN<α的模糊系数
规则4. IF<迭代次数为“中后”>, THEN<α的模糊系数
规则5. IF<如果迭代次数为“后”>, THEN<α的模糊系数
最后, 使用Matlab的模糊控制器工具箱完成模糊控制器的设计, 解模糊采取“重心法”.
2.3 FWGWO算法描述综上所述, FWGWO的算法描述如下:
算法1. FWGWO算法
1) 初始化种群规模N, 随机产生初始种群, 初始化t=0, 初始化
2) 计算种群中每个个体的适应度值, 将适应度排名前三的个体分别记为Xα, Xβ和Xδ;
3) 由式(6)–(8)计算种群中其他个体与Xα, Xβ和Xδ的距离, 并根据式(9)–(11)更新个体位置.
4) 由模糊控制器获得决策层Xα, Xβ和Xδ的权重系数, 由式(14)完成目标定位.
5) 更新算法中
6) 判定算法是否满足收敛条件. 如果满足, 则算法结束; 否则, 令t=t+1, 返回第3)步.
3 实验及分析本文采用Matlab R2012b进行仿真, 运行环境为Intel(R) Corel(TM) i7-3770处理器, 3.5 GHZ内存. 测试集为CEC2005, 将GWO算法、粒子群算法(Particle Swarm Optimization, PSO)及FWGWO算法对测试集中的23个标准测试函数进行测试, 其中F1–F7为单峰函数, F8–F13为多峰函数, F14–F23为固定维数多峰函数, 篇幅原因, 测试函数的定义、维度及最小值等参数详见文献[1].
仿真实验设置种群数目为30, 迭代次数为500, 测试函数的维度按文献[1]中设置. 几种算法的参数设置如下: PSO算法中设置ωmax=0.9, ωmin=0.2, c1=c2=2; GWO算法和FWGWO算法设置
表 1给出了三种算法针对13个标准测试函数独立运行50次的均值和标准差, 其中F1–F7为单峰标准函数, F8–-F13为多峰标准函数.
表 2给出了三种算法针对10个固定维数多峰函数独立运行50次的均值和标准差.
| 表 1 三种算法针对13个标准函数的测试结果 |
| 表 2 三种算法针对固定维数多峰测试函数的测试结果 |
由表 2可以看出, FWGWO算法对于大部分函数均取得较好的寻优结果, 特别是对于单峰标准函数F1-F4, FWGWO算法性能明显优于对比算法. FWGWO和GWO算法在F1、F2、F3、F4、F10上可判定为找到全局最优解, 而FWGWO算法相对于基本GWO算法具有更好的求解精度. 对于F9、F11, 在100次独立测试中, FWGWO算法寻优正确率分别是91%、93%, 而GWO算法寻优正确率分别为51%、72%. 由此可知, FWGWO算法相较于GWO算法, 在大部分函数的寻优性能上有明显提升. PSO算法在测试函数F6、F12、F13取得较好的寻优结果, 但整体看来, FWGWO算法在大部分函数的寻优结果均优于PSO算法.
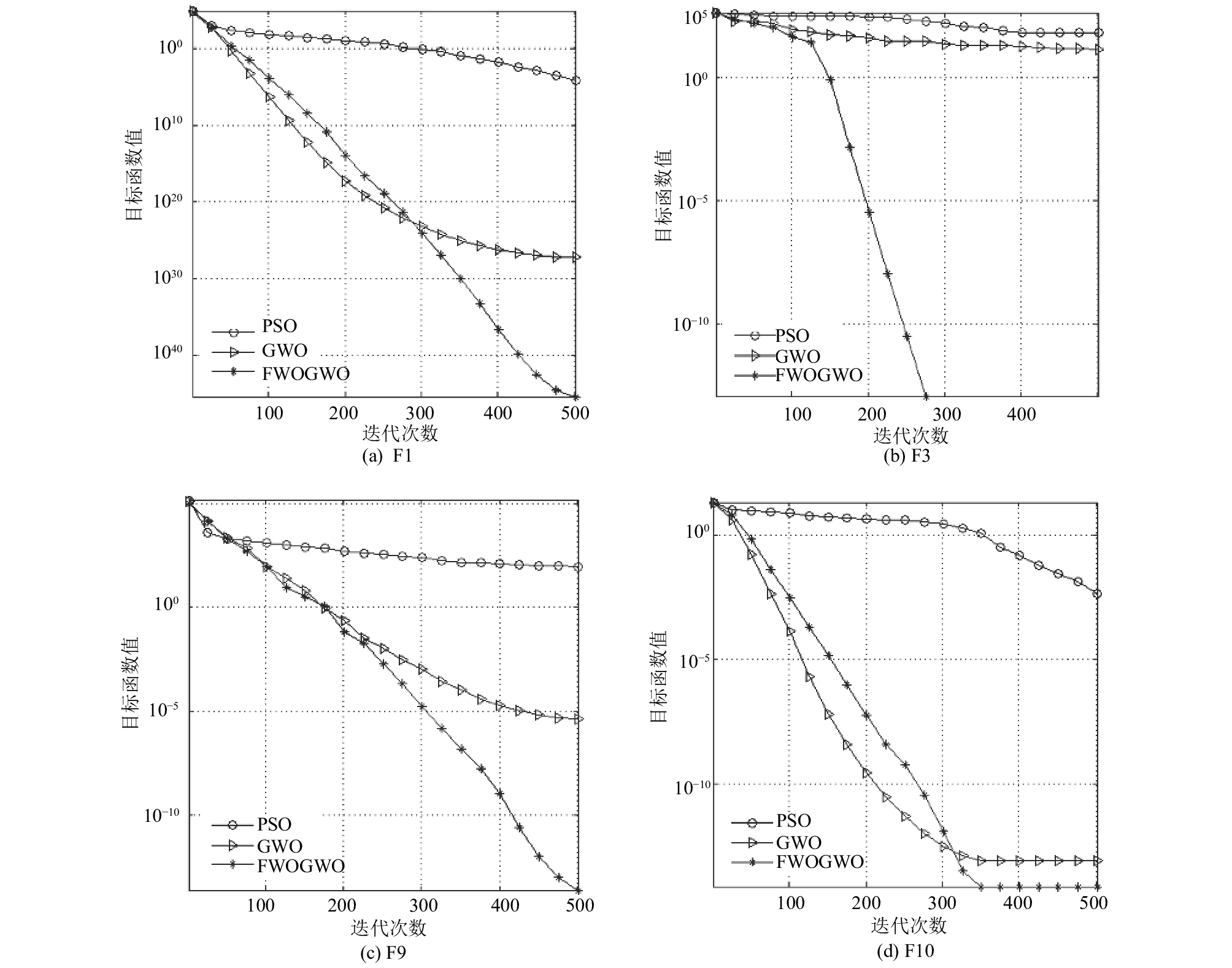
由表3可以看出, FWGWO算法在测试函数F16-F23都能收敛到函数最小值, 对于测试函数F14、F15基本接近函数最小值. 相比于对比算法, FWGWO算法在大部分函数具有更好的求解精度. 图 6示意了三种算法针对不同测试函数的收敛曲线, 展示了算法针对两个单峰测试函数F1、F3和两个多峰测试函数F9、F10的收敛曲线.
由图 6可以看出, FWGWO算法相较于对比算法, 算法后期具有更快的收敛速度, 且能取得更好的寻优结果. 综合以上分析可知, 相较于PSO算法和GWO算法, FWGWO算法具有更好的算法寻优性能和算法稳定性.
4 结论与展望本文提出一种改进的灰狼优化算法, 提出了一种新的收敛因子以及一种基于动态权重的种群位置更新策略, 通过模糊控制器获得决策个体的权重系数, 使决策时更好地体现决策个体的差异性, 从而使种群更新位置更准确. 算法在23个标准测试函数上的实验结果表明, 本文提出的模糊权重灰狼优化算法FWGWO与对比算法相比, 具有更好的寻优性能和更好的稳定性.
|
图 6 算法针对不同函数的收敛曲线示意图 |
| [1] |
Goldberg DE. Genetic algorithms in search, optimization, and machine learning. Boston: Addison-Wesley Professional, 1989: 2104–2116.
|
| [2] |
Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of ICNN’95-International Conference on Neural Networks. Perth, WA, Australia. 2002. 1942–1948.
|
| [3] |
Dorigo M, Birattari M, Stutzle T. Ant colony optimization. IEEE Computational Intelligence Magazine, 2006, 1(4): 28-39. DOI:10.1109/MCI.2006.329691 |
| [4] |
Bertsimas D, Tsitsiklis J. Simulated Annealing. Statistical Science, 1993, 8(1): 10-15. DOI:10.1214/ss/1177011077 |
| [5] |
Yang XS. A new metaheuristic bat-inspired algorithm. In: González JR, Pelta DA, Cruz C, et al, eds. Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). Berlin: Springer, 2010. 65–74.
|
| [6] |
Yang XS. Firefly algorithms for multimodal optimization. In: Watanabe O, Zeugmann T, eds. Stochastic Algorithms: Foundations and Applications. Berlin: Springer. 2010. 169–178.
|
| [7] |
Yang XS, Deb S. Cuckoo search via levy flights. World 2009 Congress on Nature & Biologically Inspired Computing. Coimbatore, India. 2010. 210–214.
|
| [8] |
Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007 |
| [9] |
Komaki GM, Kayvanfar V. Grey wolf optimizer algorithm for the two-stage assembly flow shop scheduling problem with release time. Journal of Computational Science, 2015, 8: 109-120. DOI:10.1016/j.jocs.2015.03.011 |
| [10] |
Daniel E, Anitha J, Kamaleshwaran KK, et al. Optimum spectrum mask based medical image fusion using gray wolf optimization. Biomedical Signal Processing and Control, 2017, 34: 36-43. DOI:10.1016/j.bspc.2017.01.003 |
| [11] |
Shayeghi H, Asefi S, Younesi A. Tuning and comparing different power system stabilizers using different performance indices applying GWO algorithm. International Comprehensive Competition Conference on Engineering Sciences. Anzali, Iran. 2016.
|
| [12] |
Mirjalili S. How effective is the grey wolf optimizer in training multi-layer perceptrons. Applied Intelligent, 2015, 43(1): 150-161. DOI:10.1007/s10489-014-0645-7 |
| [13] |
Faris H, Aljarah I, Al-Betar MA, et al. Grey wolf optimizer: A review of recent variants and applications. Neural Computing and Applications, 2018, 30(2): 413-435. DOI:10.1007/s00521-017-3272-5 |
| [14] |
Kohli M, Arora S. Chaotic grey wolf optimization algorithm for constrained optimization problems. Journal of Computational Design and Engineering, 2017. DOI:10.1016/j.jcde.2017.02.005 |
| [15] |
Natesan G, Chokkalingam A. Opposition learning-based grey wolf optimizer algorithm for parallel machine scheduling in cloud environment. International Journal of Intelligent Engineering and Systems, 2017, 10(1): 186-195. DOI:10.22266/ijies2017.0228.20 |
| [16] |
龙文, 蔡绍洪, 焦建军, 等. 求解高维优化问题的混合灰狼优化算法. 控制与决策, 2016, 31(11): 1991-1997. |
| [17] |
Mittal N, Singh U, Sohi BS. Modified grey wolf optimizer for global engineering optimization. Applied Computational Intelligence and Soft Computing, 2016, 2016(8). DOI:10.1155/2016/7950348 |
| [18] |
Singh N, Singh SB. Hybrid algorithm of particle swarm optimization and grey wolf optimizer for improving convergence performance. Journal of Applied Mathematics, 2017, 2017: 2030489. DOI:10.1155/2017/2030489 |
| [19] |
Tawhid MA, Ali AF. A hybrid grey wolf optimizer and genetic algorithm for minimizing potential energy function. Memetic Computing, 2017, 9(4): 347-359. DOI:10.1007/s12293-017-0234-5 |
| [20] |
龙文, 伍铁斌. 协调探索和开发能力的改进灰狼优化算法. 控制与决策, 2017, 32(10): 1749-1757. |
| [21] |
Muro C, Escobedo R, Spector L, et al. Wolf-pack (Canis Iupus) hunting strategies emerge from simple rules in computational simulations. Behavioural Processes, 2011, 88(3): 192-197. DOI:10.1016/j.beproc.2011.09.006 |
| [22] |
石绍应, 王小谟, 曹晨, 等. 规则数确定的自适应模糊分类器. 西安电子科技大学学报(自然科学版), 2017, 44(2): 81-87. |
 2018, Vol. 27
2018, Vol. 27

