图像配准是图像处理中的一种重要的处理技术, 一般指将不同时间、不同传感器(成像设备)或不同条件下(天候、照度、摄像位置和角度等)获取的两幅或多幅图像进行匹配、叠加的过程, 它已经被广泛地应用于计算机视觉、遥感图像处理等领域. 其中,图像之间的特征匹配是图像配准的重要研究内容.
Lowe[1]在1999年提出的SIFT算法是图像匹配算法中鲁棒性比较好的一种算法, 也是目前比较成功的一种算法, 该算法具有良好的平移特性, 并且对光照、尺度变化保持不变性. 但是SIFT算法对每个关键点形成一个4×4×8=128维的描述子, 计算量大;同时, 对于边缘点较少的图像, 提取的关键点较少. 因此, 国内外许多学者针对SIFT算法进行了深入的研究, 并提出了许多改进算法[2–15]. 例如, Bay等[2]提出了SURF算法, 其通过计算积分图像和Fast-Hessian矩阵, 大大提高了关键点检测速度, 但它的旋转不变性比SIFT算法差. YanKe[3]在2004年提出了PCA-SIFT算法, 其对SIFT特征描述符采用PCA降维, 大幅减少了运算时间, 但角点的检测精度有所降低, 在实际应用中效果不太理想. 林晓帆[4]提出了基于SURF描述子的遥感图像配准, 在算法匹配效率上得到了极大的改进, 但该算法重点关注遥感图像的配准. 芮挺[5]等提出了基于SIFT描述的Harris角点多源图像配准, 在匹配效率和精度两方面都有很好的改进. 张少敏[6]提出了融合SIFT特征的熵图估计医学图像非刚性匹配, 实现了具有良好鲁棒性的医学图像配准. 这些都是基于某个领域内对匹配算法的改进, 适用范围有一定的局限性. 还有学者[7–10]提出对数据进行分组处理, 但是没有对分组进行规则限制, 导致匹配率降低.
本文将SIFT算法的128维数据根据8个梯度方向分成8组, 并根据梯度模值的大小对这8个梯度方向建立索引, 将索引添加入关键点的信息结构中. 重新定义每个关键点的信息, 产生新的有序描述子, 进而提出一种改进的SIFT算法.
2 SIFT算法简介 2.1 尺度空间极值检测为了进行图像尺度空间极值检测, 首先要对图像建立尺度空间; 尺度空间理论目的是模拟图像数据的多尺度特征. 采用高斯卷积核是实现尺度变换, 将一副二维图像的尺度空间定义为;
| $L(x,y,\delta ) = G(x,y,\delta )*I(x,y)$ | (1) |
其中,
| $G(x,y,\delta ) = \frac{1}{{2\pi {\delta ^2}}}{e^{ - ({x^2} + {y^2})/2{\delta ^2}}}$ | (2) |
式(1)(2)中δ大小决定图像的平滑程度, δ值越大图像分辨率越低,
| $\begin{aligned} D(x,y,\delta ) & = (G(x,y,k\delta ) - G(x,y,\delta ))*I(x,y) \\ & = L(x,y,k\delta ) - L(x,y,\delta ) \\ \end{aligned} $ | (3) |
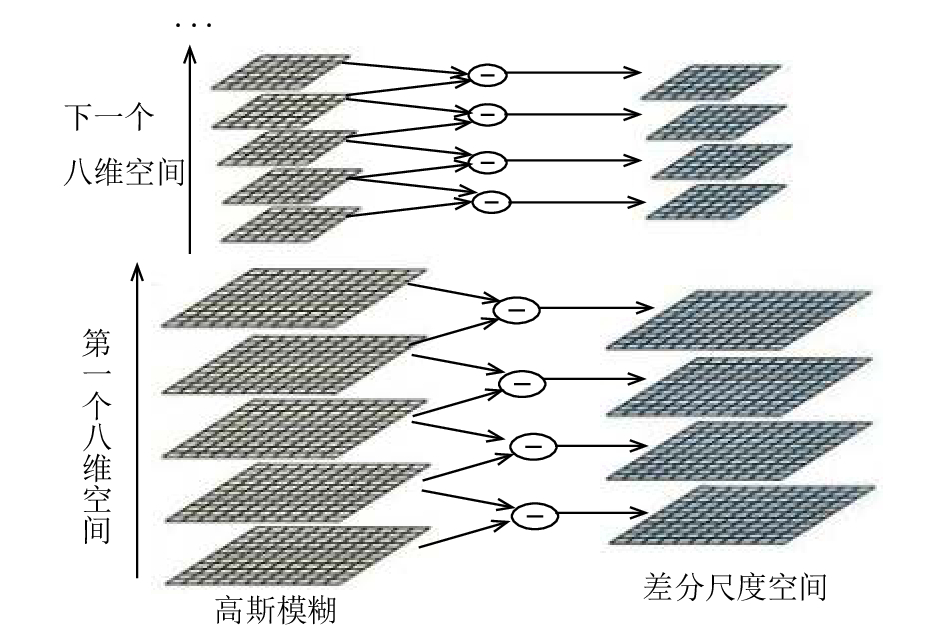
对于任意图像, 建立其高斯差分尺度空间, 即图像金字塔, 如图1所示.
|
图 1 高斯差分尺度空间 |
2.2 关键点生成
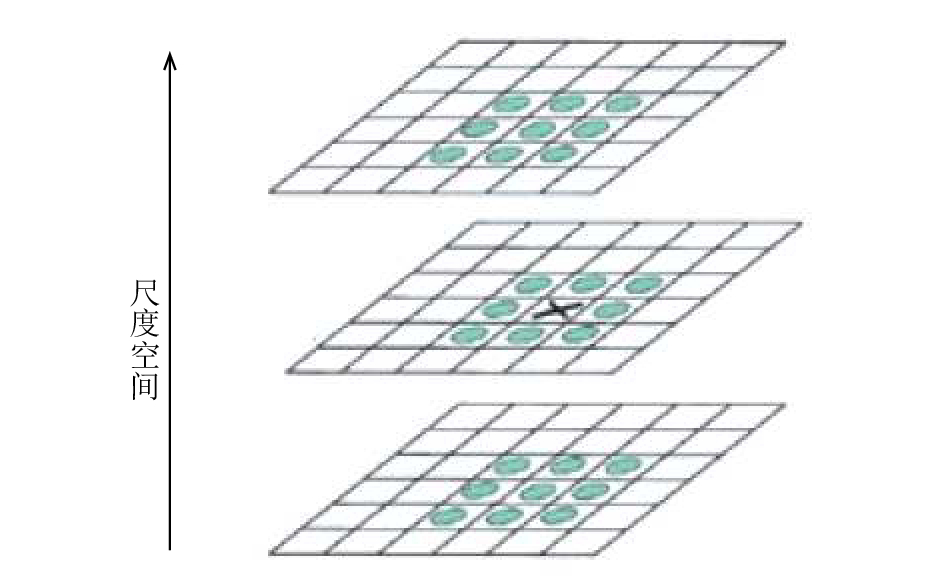
(1)关键点检测; 为了寻找尺度空间的极值点, 每一个采样点要和它所有的相邻尺度对应的26个点进行比较, 如果它是其中的最大或最小值时, 就认为该点是图像在该尺度下的一个关键点, 图2所示为尺度空间寻找到极值点.
|
图 2 关键点 |
在极值比较的过程中, 每一组图像的首末两层是无法进行极值比较的, 为了满足尺度变化的连续性, 在每一组图像的顶层继续用高斯模糊生成了3幅图像.
(2)不合格关键点的剔除; 利用泰勒二次展开式(公式(4))拟合曲线, 然后通过该点尺度位置2×2的Hessian矩阵(公式(5))计算其主曲率, 来去掉高斯差分尺度空间局部曲率不对称的关键点.
| $D(x) = D + \frac{{\delta {D^{\rm{T}}}}}{{\delta x}}x + \frac{1}{2}{x^T}\frac{{{\delta ^2}D}}{{\delta {x^2}}}x$ | (4) |
| $H = \left[ {\begin{array}{*{20}{c}}{{D_{xx}}}&{{D_{xy}}}\\{{D_{xy}}}&{{D_{yy}}}\end{array}} \right]$ | (5) |
(1)确定关键点主方向; 关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数, 使算子具备旋转不变性. 利用梯度直方图统计邻域像素的梯度方向, 梯度直方图的范围是0~360度, 其中每45度一个柱, 总共8个柱, 或者每10度一个柱, 总共36个柱, 计算时一般采用8个柱的方式. 公式(6)和公式(7)为幅值和梯度方向计算方法.
| $\begin{array}{l}m(x,y) =\\\sqrt {{{(L(x + 1,y) - L(x - 1,y))}^2} + {{(L(x,y + 1) - L(x,y - 1))}^2}} \end{array}$ | (6) |
| $\begin{array}{l}\theta (x,y) =\\\alpha \tan 2((L(x,y + 1) - L(x,y - 1))/(L(x + 1,y) - L(x - 1,y)))\end{array}$ | (7) |
(2)直方图中的峰值就是主方向, 其他达到最大值80%的可作为辅助方向. 这时, 每个关键点有三个特征信息; 位置、所处尺度、方向.
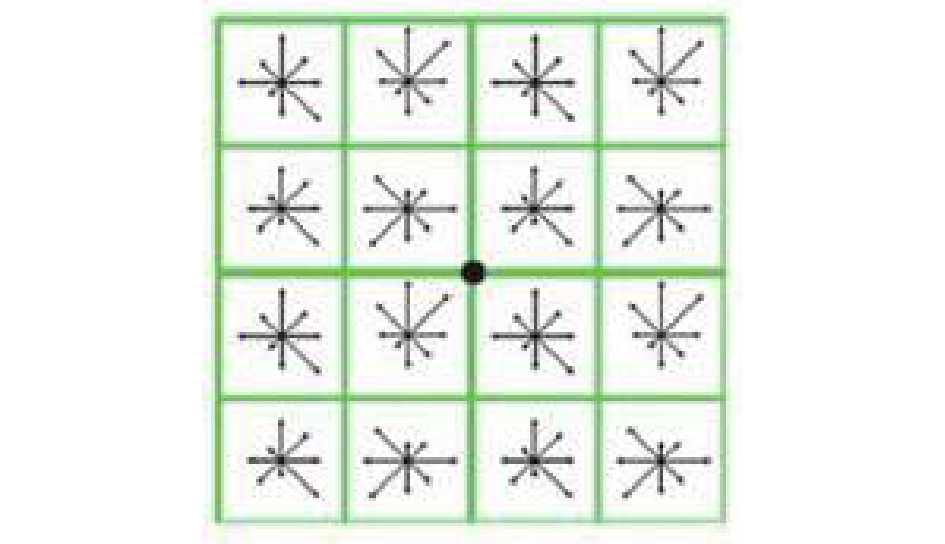
(3)建立描述子; 确立好主方向后, 将坐标轴旋转为关键点的方向, 以确保图像旋转不变性. 以关键点为中心取4×4的像素点区域, 如图3所示. Lowe[1]建议描述子使用在关键点尺度空间内4×4的像素点区域中计算的8个方向的梯度信息, 共4×4×8=128维向量表征.
|
图 3 关键点的4×4像素点区域 |
3 算法的改进
通过以上对SIFT算法的理解与分析, 本文将从两个方面进行改进.
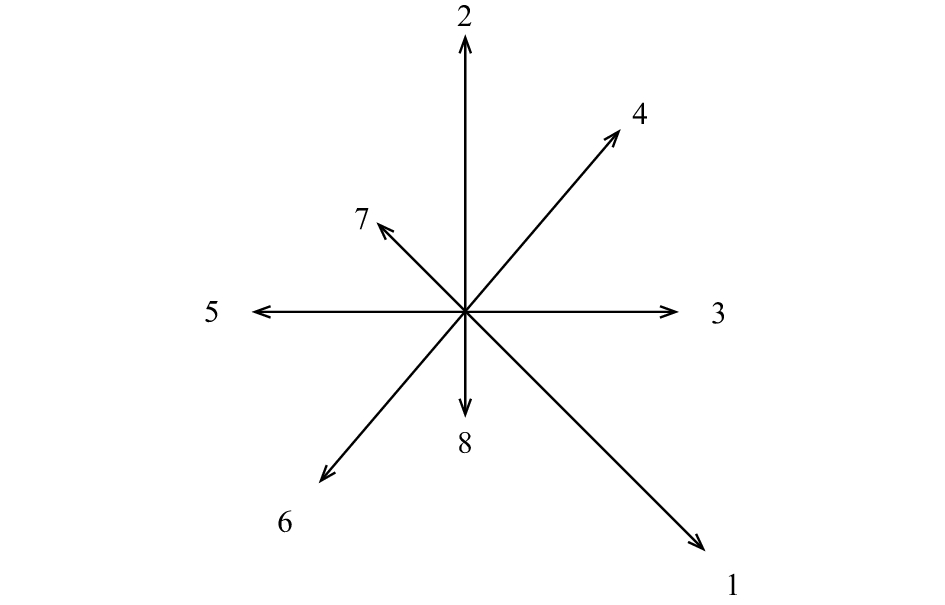
(1)关键点特征信息的改造; 原算法每个关键点包含三个特征信息; 位置、所处尺度、方向. 由于梯度模值越大, 即箭头越长, 所表示该方向所占关键点方向比重越大. 因此, 本文根据梯度模值即箭头长度大小, 由大到小建立索引(如图4所示), 若大小相同, 则按照逆时针方向顺序设置. 加入索引后, 并不改变该关键点的主方向. 加入索引后, 方便在进行匹配时的检索处理, 提高运行效率. 因此, 本文每个关键点包含四个特征信息; 位置、所处尺度、方向、索引.
|
图 4 关键点梯度方向的索引 |
(2)关键点描述子的分解; 原SIFT算法表征描述子的是128维向量. 根据关键点梯度方向的8个索引方向, 可将原描述子的128维向量分成8组16维的向量. 每组数据可以单独计算, 也可以并行处理, 提高效率. 这样, 得到关键点的8组16维向量的描述子.
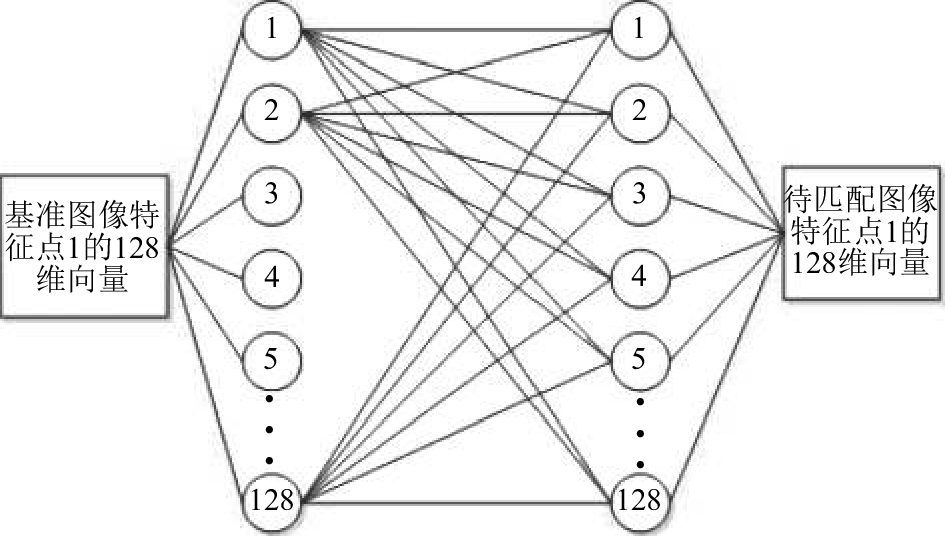
4 算法的实现原SIFT算法在图像关键点进行匹配时, 基准图像中关键点描述子表示为向量;
|
图 5 原SIFT算法的匹配方式 |
从原SIFT算法的匹配方式(图5)和本文算法的匹配方式(图6)可以看出, 原算法采用的是全匹配方式, 对两个SIFT特征向量采用1NN的匹配方式, 这样在关键点较多情况下, 会大大增加运行负担. 而在加入索引后, 根据索引不同, 只需要计算其索引相同的16维数据, 这样大大提高了运行效率. 实验表明, 在关键点达到2000时, 匹配速度提高了大约57.1%左右.
在图像匹配过程中, 本文算法在原SIFT算法的基础上进行了删除匹配成功的关键点处理, 这样可以减少循环匹配次数.
当两幅图像进行图像匹配时, 其处理步骤如下;
1) 建立尺度空间, 得到极值点, 根据Hessian 矩阵得到图像的关键点;
2) 根据关键点邻域梯度方向, 利用梯度直方图, 得到关键点的梯度方向;
3) 根据关键点的梯度方向建立索引, 构建关键点的四个特征信息; 位置、所处尺度、方向、索引;
4) 根据索引号, 建立关键点的8组16维向量的描述子;
5) 根据关键点的描述子进行匹配.
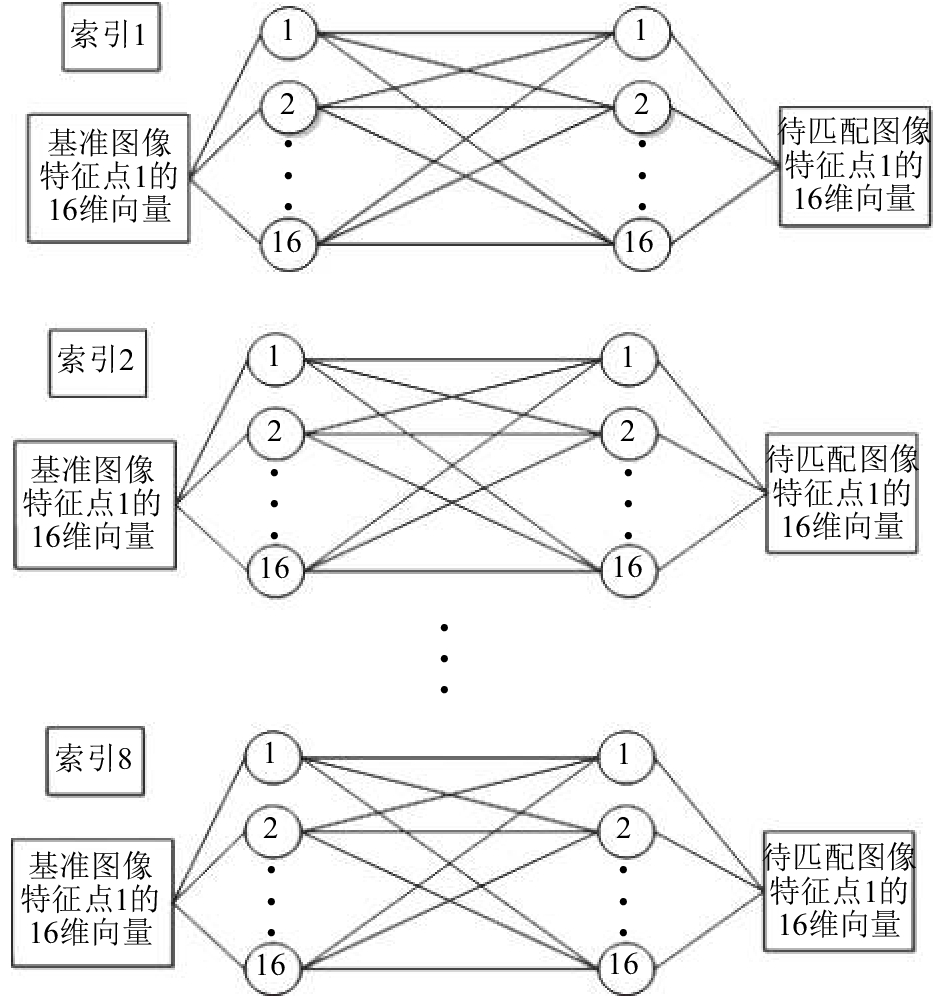
|
图 6 本文算法的匹配方式 |
5 实验结果及分析
本文实验平台为64位Windows 8 操作系统, 酷睿i5-4210U处理器, 4G内存, 采用VS2010+OPENCV 2.4.9的编译环境, 保证实验环境一致.
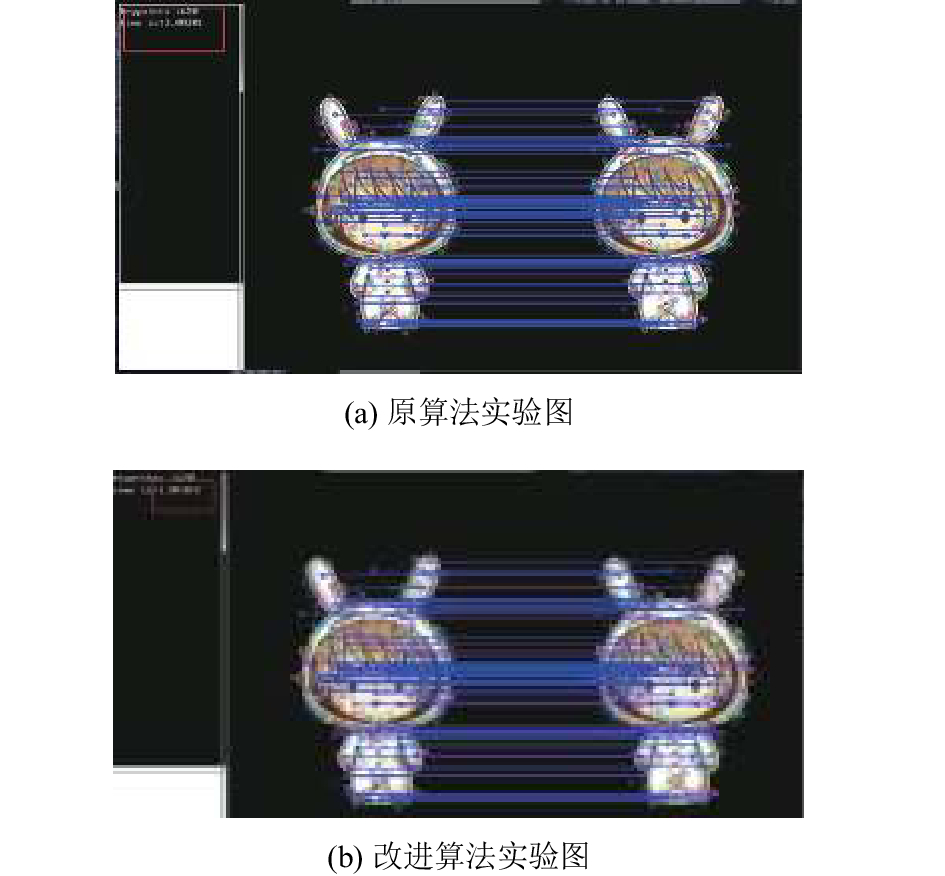
5.1 不同关键点数量测试本组实验为图片不做变动, 但是图像关键点不一致, 将匹配点数设置为100进行测试, 计算原SIFT算法和本文的改进SIFT算法图像匹配所需运行时间, 实验结果如图7至图9和表1所示. 图7(a)表示为原算法运行时间, (b)表示为改进后关键点数在600左右时算法的运行时间; 图8(a)表示为原算法运行时间, (b)表示为改进后关键点数在1700左右时算法的运行时间; 图9(a)表示为原算法运行时间, (b)表示为改进后关键点数在2100左右时算法的运行时间.
|
图 7 A组实验对比图 |

|
图 8 B组实验对比图 |
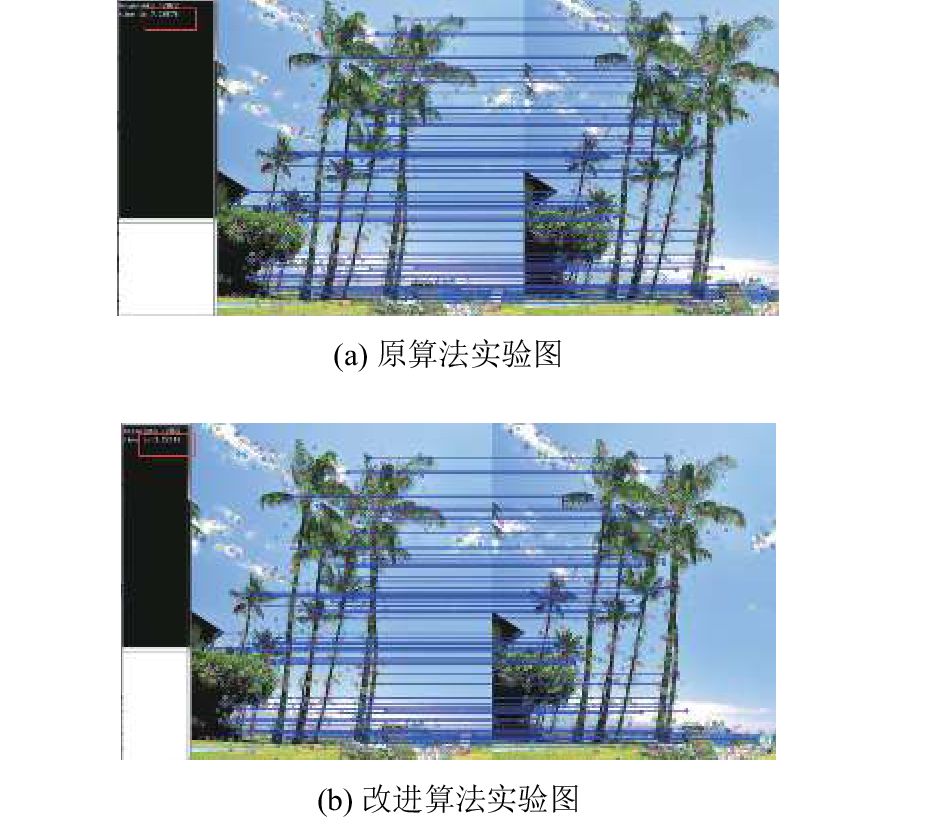
|
图 9 C组实验对比图 |
| 表 1 关键点不一致时的匹配数据 |
实验数据表明, 当关键点为600左右时, 改进后算法运算时间大概减少了2秒, 运算速度提高了66.7%, 当关键点在1500左右时, 算法运行时间提高了2.8秒左右, 运算速度提高了51.9%, 当关键点在2000以上时, 算法运行时间提高了4.02秒左右, 运算速度提高了57.1%左右.
5.2 像尺度变换后的配准测试本组实验将图片旋转之后进行测试. 其中A组为原图向右旋转10度, 设置匹配点数为100得到的匹配结果. B组为原图向左旋转30度, 设置匹配点数为20得到的匹配结果. 实验结果如图10, 图11和表2所示.
图10第一幅图表示原图向右旋转10度, 设置匹配点数为100后, 原算法得到的匹配结果, 第二幅图表示改进后算法所得到的匹配结果. 图11第一幅图表示原图向左旋转30度, 设置匹配点数为20后原算法得到的匹配结果, 第二幅图表示改进后算法所得到的匹配结果. 本组实验表明, 改进后的算法依旧对图像旋转, 拉伸具备良好的鲁棒性, 但当匹配数据不大时, 所获得的时间提升没有太过明显. 当数据量越来越大时, 算法在运算速度上的优势才能得到体现.

|
图 10 A组原算法与改进后算法的对比 |

|
图 11 B组原算法与改进后算法的对比 |
| 表 2 图像尺度变换后的配准测试数据 |
5.3 光照、遮蔽测试
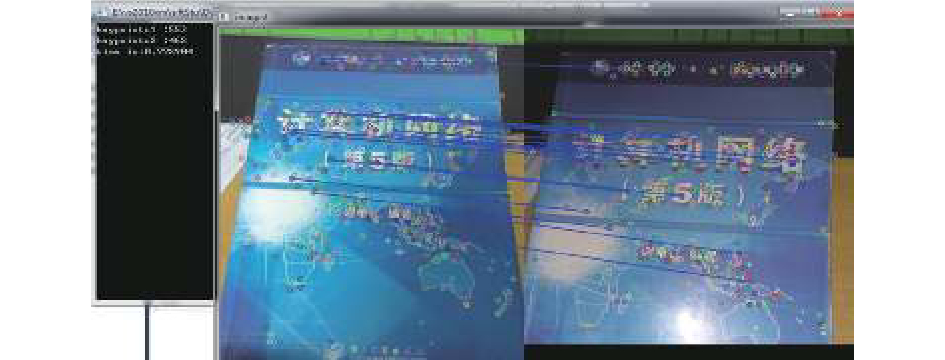
本组实验目的是测试改进算法对于光照变化和遮蔽是否仍然具备鲁棒性, 其中A组实验为光照变换之后, 改进后算法是否依然具备鲁棒性, 以及与原算法之间的对比, B组实验为当有遮蔽物时的测试. 实验结果如图12至图15和表3所示. 图12表示为原算法在光照变化情况下的匹配结果; 图13表示为改进后算法在光照变化情况下的匹配结果; 图14表示为原算法在遮蔽情况下的匹配结果; 图15表示为改进后算法在遮蔽情况下的匹配结果.

|
图 12 A组原算法光照 |
|
图 13 A组改进后算法光照 |

|
图 14 B组原算法遮蔽 |

|
图 15 B组改进后算法遮蔽 |
A组实验表明, 改进后算法对光照变换依然具备较好鲁棒性, 同时, 在关键点大概在500左右时, 相较于原算法运行时间提高了大约0.5秒. B组实验证明了改进后算法对于图像在有遮蔽情况下, 依然具备良好的鲁棒性, 相较于原算法运行时间缩短了大约0.4秒, 验证了改进后算法确实加快了运行速度, 降低了时间复杂度, 表明了采用本文降维的方式能提高算法的效率.
| 表 3 光照、遮蔽测试数据 |
5.4 加入椒盐噪声测试
本文利用opencv在图像中加入椒盐噪声, 来测试改进算法是否具备鲁棒性. 实验结果如图16和表4所示. 图16第一幅图表示加入噪声后原算法得到的匹配结果, 第二幅图表示改进后算法所得到的匹配结果.

|
图 16 A组实验对比图 |
| 表 4 加入噪声测试数据 |
从表4可以看出, 改进后算法任然对噪声图像保持鲁棒性, 在配准时间上依然具备竞争力, 配合索引, 在效率方面得到了很大的提高.
6 结束语本文针对图像配准经典算法-SIFT算法中关键点的特征信息进行改造, 并将原描述子的128维数向量据根据8个梯度方向分成8组, 建立分组的描述子向量, 提出了一种改进的SIFT算法. 数值实验表明, 本文改进后的算法能够在保持原算法的光照不变性、旋转不变性、以及关键点的匹配精度的情形下, 有效地提高了算法的效率.
| [1] |
Lowe DG. Recognition from local scaleinva riant features. International Conference on Computer Vision. Corfu, Greece. 1999. 1150–1157.
|
| [2] |
Bay H, Tuytelaars T, Van Gool L. SURF: Speeded up robust features. In: Leonardis A, Bischof H, Pinz A, eds. Computer Vision–ECCV 2006. Berlin: Springer, 2006. 404–417.
|
| [3] |
Ke Y, Sukthankar R. PCA-SIFT: A more distinctive representation for local image descriptors. Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC, USA. 2004. 511–517.
|
| [4] |
林晓帆, 林立文, 邓涛. 基于SURF描述子的遥感影像配准. 计算机工程, 2010, 36(12): 216-218. DOI:10.3969/j.issn.1000-3428.2010.12.074 |
| [5] |
芮挺, 张升奡, 周遊, 等. 具有SIFT描述的Harris角点多源图像配准. 光电工程, 2012, 39(8): 26-31. DOI:10.3969/j.issn.1003-501X.2012.08.004 |
| [6] |
张少敏, 支力佳, 赵大哲, 等. 融合SIFT特征的熵图估计医学图像非刚性配准. 中国图像图形学报, 2012, 17(3): 412-418. |
| [7] |
谢宜婷, 王爱平, 邹海. 基于局部近邻图的特征描述与特征匹配算法研究. 计算机应用与软件, 2017, 34(8): 185-190, 196. DOI:10.3969/j.issn.1000-386x.2017.08.033 |
| [8] |
Ge S, Fan G, Ding M. Non-rigid point set registration with global-local topology preservation. 2014 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Columbus, OH, USA. 2014. 245–251.
|
| [9] |
Yu TS, Wang RS. Enhancing scene parsing by transferring structures via efficient low-rank graph matching. Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Burlingame, CA, USA. 2016.
|
| [10] |
涂秋洁, 王晅. 基于PCA-SIFT特征与贝叶斯决策的图像分类算法. 计算机应用与软件, 2016, 33(6): 215-219. DOI:10.3969/j.issn.1000-386X.2016.06.052 |
| [11] |
Zhang XH, Wang XQ, Yuan XX, et al. An improved SIFT algorithm in the application of close-range stereo image matching. IOP Conference Series Earth and Environmental Science, 2016, 46(1): 012009. DOI:10.1088/1755-1315/46/1/012009 |
| [12] |
Lei H, Xu ZH, Feng HJ, et al. Template-based image registration in an optical butting system. Journal of Optoelectronics·Laser, 2010, 21(11): 1725-1729. |
| [13] |
Kumar RRP, Muknahallipatna S, McInroy J. An approach to parallelization of sift algorithm on GPUS for real-time applications. Journal of Computer and Communications, 2016, 4(17): 18-50. DOI:10.4236/jcc.2016.417002 |
| [14] |
Koenderink JJ. The structure of images. Biological Cybernetics, 1984, 50(5): 363-396. DOI:10.1007/BF00336961 |
| [15] |
Lindeberg T. Scale-space theory: A basic tool for analyzing structures at different scales. Journal of Applied Statistics, 1994, 21(1-2): 224-270. |
 2018, Vol. 27
2018, Vol. 27


