想象一个人机对话系统, 当计算机在屏幕上显示:
Please turn your homework …
大部分人认为homework后面应该接to或者是over, 但是不可能是on. 那么计算机处理这个任务时, 它根据什么来决定后面接什么?
让计算机处理自然语言的一个基本问题是为自然语言这种上下文有关的特性建立数学模型——统计语言模型, 它是今天所有自然语言处理任务的基础. 在20世纪70年代由贾里尼克提出的N-gram模型是最常用的统计语言模型之一, 广泛用于当今的多种自然语言处理系统中[1]. 目前关于N-gram模型应用的研究有机器翻译自动评分, 摘要生产系统自动评分, 单词分类, 文本分类等[2–5], 但是却没有对于N-gram模型主要平滑方法的综合介绍, 所以本文着重介绍了几种常用的平滑方法.
计算机利用N-gram模型计算出后面每个可能的词的概率, 并选择概率最大的词放到homework后面, N-gram模型还用于计算整个句子在语料库中出现的概率, 比如下面两条语句:
S1: I am watching movie now.
S2: watching I am now movie.
N-gram模型会预测句子S1的概率
在语音识别和手写识别任务中, 我们需要估算出每个词w的概率
在拼写纠错系统中, 我们需要找出并纠正句子中拼错的词, 比如句子:
S3: Their are so many people.
S4: There are so many people.
在句子S3中计算机认为There被错拼成了Their了, 因为S4出现的概率
在机器翻译任务中, 需要确定每个词序列的概率以找出最正确的翻译结果:
S5: 我今天要去上学.
S6: I today want go on learn.
S7: I today want go to school.
S8: I am going to school today.
由于在英语短语中, go to school出现的概率要比go on learn大以及时间通常放在句尾, 所以计算机认为
N-gram模型常用于估算给定语句在语料库中出现的概率, 一个N-gram是一个长为N的词序列. 当N=1时称为Unigram模型即一元模型, 也叫上下文无关模型; 当N=2时称为bigram模型即二元模型; 当N=3时称为trigram模型即三元模型.
1 N-gram模型N-gram模型的基本原理是基于马尔可夫假设, 在训练N-gram模型时使用最大似然估计模型参数——条件概率.
1.1 基本原理假设S= w1 w2 w3…wn表示给定的一条长为n的语句, 其中
| $p(S) = p({w_1}{w_2}{w_3}\cdots{w_n}) = p(w_1^n)$ | (1) |
根据链式法则和条件概率公式, S出现的概率p(S)等于S中每个单词
| $\begin{array}{l} p(w_1^n) = p({w_1})p({w_2}|{w_1})p({w_3}|w_1^2) \cdots ({w_n}|w_1^{n - 1})\\ = \prod\nolimits_{k = 1}^n {p({w_k}|w_1^{k - 1})} \end{array}$ | (2) |
由此我们知道可以根据条件概率
所以为了简化计算的复杂度, 马尔可夫提出了马尔可夫假设: 假设任意一个单词
| $p({w_n}|w_1^{n - 1}) \approx p({w_n}|{w_{n - 1}})$ | (3) |
基于马尔可夫假设得到的是二元模型:
| $\begin{aligned}p(w_1^n) & \approx p({w_1})p({w_2}|{w_1})p({w_3}|{w_2}) \cdots p({w_n}|{w_{n - 1}})\\& = \prod\nolimits_{k = 1}^n {p({w_k}|{w_{k - 1}})} \end{aligned}$ | (4) |
马尔可夫的假设有不足之处, 比如“happy new year”中“year”其实和“new”与“happy”都有关, 因此柯尔莫果洛夫将马尔可夫假设推广到一般形式: 假设句子中的每个单词与其前面N–1个词有关:
| $p({w_n}|w_1^{n - 1}) \approx p({w_n}|w_{n - N + 1}^{n - 1})$ | (5) |
这称为N–1阶马尔可夫假设[6].
1.2 参数估计在训练N-gram模型时, 一个重要的问题就是模型的参数估计即估计条件概率. 以二元模型为例, 需要估计条件概率
| $p({w_i}|{w_{i - 1}}) = \frac{{p({w_{i - 1}}, {w_i})}}{{p({w_i})}} = \frac{{c({w_{i - 1}}, {w_i})}}{{c({w_i})}}$ | (6) |
假设一个只有三条语句的语料库, 每条语句以<s>开头, 以</s>结束:
<s> I am Sam </s>
<s> Sam I am </s>
<s> I do not like green eggs and ham </s>
则二元模型计算出的部分条件概率如下:
| $p(I| < s > ) = \frac{2}{3} = 0.67$ |
| $p(Sam| < s > ) = \frac{1}{3} = 0.33$ |
| $p(am|I) = \frac{2}{3} = 0.67$ |
现在我们将在实际中使用N-gram模型, 以布朗语料库的新闻类别为训练语料库, 该语料库的规模有10054个标识符, 以句子:
S9: I will run for the governor.
为例, 考虑二元模型, 在语料库中的各项统计数据如表1和表2所示.
| 表 1 S9中单词在训练语料库中的频数 |
| 表 2 S9中二元组在训练语料库中的频数和频率 |
表1和表2中, (#, I)表示S9以I开头, (governor, $)表示S9以governor结尾, 根据公式(6)计算S9出现的概率, 由于概率值均在0~1之间, 导致多个概率相乘的结果会非常小, 所以我们对最终的概率值取以10为底的对数, 结果是–11.2849(后面概率计算结果均是取对数后的结果).
在实际应用中, 通常使用三元模型的居多, 谷歌公司的翻译系统则使用四元模型, 这个模型存储在500台以上的服务器中.
1.3 零概率问题假设有如下语句:
S10: Will I run the for governor.
考察一下它出现的概率
| 表 3 S10中二元组在训练语料库中的频数和频率 |
统计时出现了很多频数为零从而导致频率为零的结果, 即所谓的零概率问题.
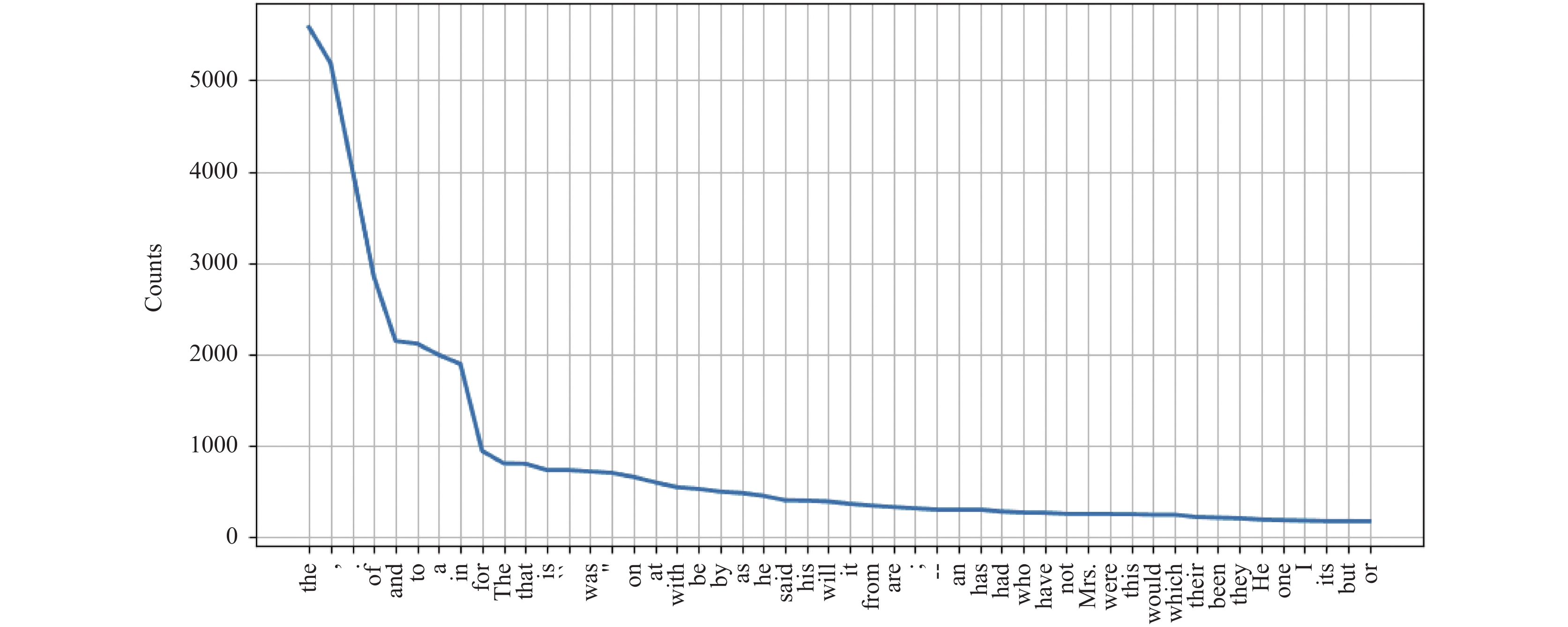
布朗语料库的新闻类别中使用最频繁的前50个单词的频数变化(包括标点符号)如图1所示.
|
图 1 单词频数变化 |
在该语料库中只有极少数单词被经常使用, 而绝大多数单词很少被使用, 这就是著名的Zipf定律: 一个单词出现的次数与它在频率表里的排名成反比. 假设在语料库中出现r次的词有
词出现的次数r与词的数量
| $\sum\nolimits_r {{N_r}} = M$ | (7) |
那么出现r次的词在语料库中的频率为
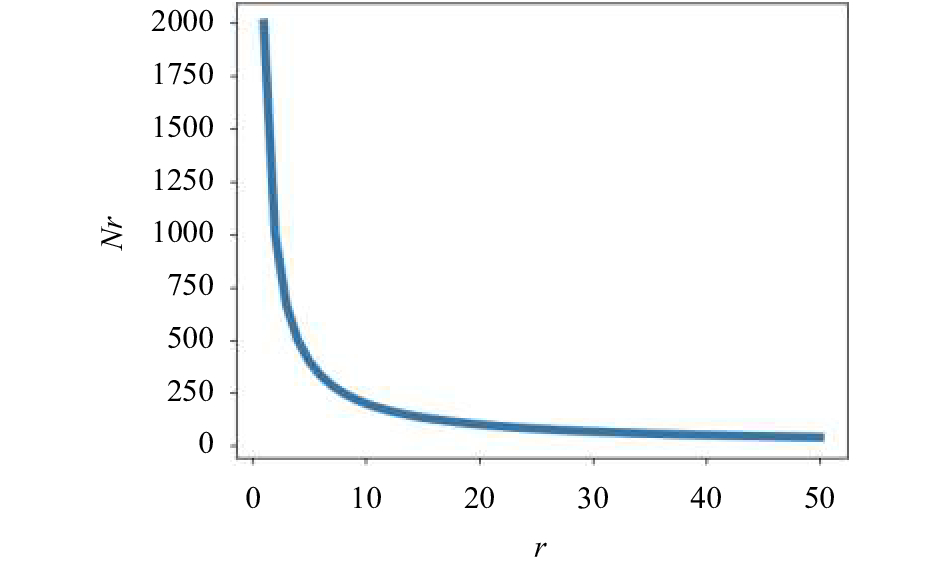
|
图 2 Zipf定律 |
2 N-gram模型的评价标准
评价一个语言模型的最佳评价方法是把模型应用到实际的产品中, 比较该产品在应用模型前后的性能提高程度, 这称为外部评价. 但是在实验中, 由于资源的限制我们无法使用外部评价, 更多的是使用内部评价方法, 即在测试集上使用困惑度作为语言模型的评价准则.
假设测试集
| $\begin{array}{l} PP(W) = P{({w_1}{w_2}{w_3} \cdots {w_N})^{ - \frac{1}{N}}}\\ = \sqrt[N]{{\frac{1}{{P({w_1}{w_2}{w_3} \cdots {w_N})}}}} \end{array}$ | (8) |
然后使用链式法则扩展:
| $PP(W) = \sqrt[N]{{\prod\nolimits_{i = 1}^N {\frac{1}{{P({w_1}{w_2}{w_3}\cdots{w_N})}}} }}$ | (9) |
因此, 应用到二元模型就得到:
| $PP(W) = \sqrt[N]{{\prod\nolimits_{i = 1}^N {\frac{1}{{P({w_i}|{w_{i - 1}})}}} }}$ | (10) |
由式(8)可知, 一个词序列的概率越大, 它的困惑度就越小, 所以语言模型的优化目标就是最小化困惑度.
我们可以从另一个角度来看待困惑度: 语言的加权平均分支因子. 语言的分支因子指的是可以跟在任意一个词后的所有可能的词的数量. 假设有一个数字识别系统, 用来识别0, 1, 2,
| $\begin{aligned}PP(W) =& P{({w_1}{w_2}{w_3}\cdots{w_N})^{ - \frac{1}{N}}}\\ = &{({\frac{1}{{10}}^N})^{ - \frac{1}{N}}} ={(\frac{1}{{10}})^{ - 1}} = 10 \end{aligned}$ | (11) |
换句话说, 任意的一个数字后面可以接0~9共10个数字中的任意一个数字, 所以这个数字语言的分支因子是10.
我们在布朗语料库上分别训练了一元模型, 二元模型和三元模型, 它们的困惑度是
| 表 4 三种N-gram模型的困惑度 |
由此可见, N-gram模型考虑的上下文越长, 模型的困惑度就越低.
3 平滑回到前面的零概率问题, 避免零概率问题的方法之一是防止模型把没看到的事件(如二元组(Will, I))的概率算为零. 所以我们有两种解决方法, 增大语料库和改变概率估算方法.
我们加入了布朗语料库的政府文本类别和学术文本类别, 统计S2中二元组频数如表5所示.
| 表 5 S2中二元组在扩大后的语料库中的频数 |
在增加了语料库规模后, 还是没有解决零概率问题. 所以我们需要平滑: 将一部分概率分配给没看到的事件, 主要的平滑方法有拉普拉斯平滑, 卡茨回退和Kneser-Ney平滑[7–9].
3.1 拉普拉斯平滑最简单的平滑方法是规定所有的词或词对至少出现一次, 所以即使是未出现的词或词对, 它们的出现次数也被人为设定为1. 这种平滑方法称为拉普拉斯平滑. 拉普拉斯平滑在现代的N-gram模型中表现不是十分好, 但是它是所有其他平滑方法的基础, 现在仍然被广泛应用在文本分类领域中.
假设语料库规模为M, 语料库的词汇表规模为V. 对于一元模型来说, 设词
| $p({w_i}) = \frac{{{c_i}}}{M}$ | (12) |
应用拉普拉斯平滑后的概率为:
| ${p_L}({w_i}) = \frac{{{c_i} + 1}}{{M + V}}$ | (13) |
可见拉普拉斯平滑方法将所有的词计数都增加1, 这种平滑方法也叫做Add-one平滑.
为了计算的方便, 通常情况下定义一个调节计数:
| $c_i^* = ({c_i} + 1)\frac{M}{{M + V}}$ | (14) |
显然有
| ${d_c} = \frac{{c_i^*}}{{{c_i}}}$ | (15) |
现在我们将其推广到二元模型:
| ${p_L} = \frac{{c({w_{i - 1}}, {w_i}) + 1}}{{c({w_{i - 1}}) + V}}$ | (16) |
| ${c^*}({w_{i - 1}}, {w_i}) = \frac{{[c({w_{i - 1}}, {w_i}) + 1] \times c({w_{i - 1}})}}{{c({w_{i - 1}}) + V}}$ | (17) |
再次统计出S2中二元组在训练语料库中的频率, 如表6.
| 表 6 经过Add-one后的S2中二元组的频率 |
可以发现零概率问题已经被解决. 但是由于语料库中未出现的词或词对的数目太多, 拉普拉斯平滑导致为它们分配了很大的概率空间, 所以我们可以不加1, 转而选择寻找一个小于1的正数k, 此时的概率计算公式为:
| ${p_{add - k}} = \frac{{c({w_{i - 1}}, {w_i})}}{{c({w_{i - 1}}) + kV}}$ | (18) |
此时叫做Add-k平滑.
3.2 卡茨回退古德和图灵提出了一种在统计中相信可靠的统计数据, 而对不可靠的统计数据打折扣的一种概率估计方法: 从概率的总量1中分配一个很小的比例给没有看见的事件, 这样没有看见的事件也拥有了很小的概率.
在一个语料库中出现次数越小的词, 说明这个词很少使用, 甚至是不可靠的. 所以当r较小的时候, 统计数据可能不可靠, 于是选取一个阈值
| ${r^*} = \frac{{(r + 1) \times {N_r}}}{{{N_{r + 1}}}}$ | (19) |
仍然有:
| $\sum\nolimits_r {{r^*} \times {N_r} = M} $ | (20) |
于是当
| $p({w_i}|{w_{i - 1}}) = \\\left\{ \begin{array}{l} c({w_{i - 1}}, {w_i})/c({w_{i - 1}}) , \;\;c({w_{i - 1}}, {w_i}) \geqslant \sigma \\ {{{r^*}} / {c({w_{i - 1}}) , }}\;\;0 < c({w_{i - 1}}, {w_i}) < \sigma \\ f({w_{i - 1}}, {w_i}) ,\;\; c({w_{i - 1}}, {w_i}) < 0 \end{array} \right.$ | (21) |
其中,
| $f({w_{i - 1}}, {w_i}) = (1 - r/M - {r^*}/M)$ | (22) |
当我们取
| 表 7 经过卡茨回退后的S2中二元组的频率 |
由于一个单词
比如估算三元模型的概率时, 把一元模型, 二元模型和三元模型结合起来, 每种模型赋予不同的权重
| $\begin{aligned}p({w_i}|{w_{i - 2}}, {w_{i - 1}}) = & {\lambda _1}f({w_i}) + {\lambda _2}f({w_i}|{w_{i - 1}})\\ &+ {\lambda _3}f({w_i}|{w_{i - 2}}, {w_{i - 1}}) \end{aligned} $ | (23) |
其中,
Kneser-Ney算法是目前使用最为广泛的, 效果最好的平滑方法. 它的基本思想是绝对折扣.
我们从训练语料库中随机抽取25%的数据作为验证集, 统计得出在训练集和验证集中出现次数在0~9之间的bigram的对比数据如表8.
| 表 8 bigram数据对比 |
可以看出训练集中的bigram数目在超过1后, 比验证集中bigram数目约多0.75, 所以对统计出的bigram打一个绝对折扣——总是将这0.75分配给那些没看见的bigram:
| ${p_{AD}}({w_i}|{w_{i - 1}}) = \frac{{c({w_{i - 1}}, {w_i}) - d}}{{c({w_{i - 1}})}}\\ + \lambda ({w_{i - 1}})p({w_i})$ | (24) |
其中, d可以直接设为0.75,
Kneser-Ney平滑对绝对折扣进行了改进, 给定一条语句
| ${p_{next}}({w_i}) = \frac{{\left| {\{ {w_{i - 1}}:c({w_{i - 1}}, {w_i}) > 0\} } \right|}}{{\left| {\{ ({w_{i - 1}}, {w_i}):c({w_{i - 1}}, {w_i}) > 0\} } \right|}}$ | (25) |
于是Kneser-Ney平滑为:
| ${p_{KN}}({w_{i - 1}}|{w_i}) = \frac{{\max (c({w_{i - 1}}, {w_i}) - d, 0)}}{{c({w_{i - 1}})}}\\ + \lambda ({w_{i - 1}}){p_{next}}({w_i})$ | (26) |
其中,
| $\lambda ({w_{i - 1}}) = \frac{d}{{c({w_{i - 1}})}}\left| {\{ w:c({w_{i - 1}}, w) > 0\} } \right|$ | (27) |
表示正则化的折扣量[10].
4 总结N-gram模型在目前的自然语言处理任务中使用最为广泛的统计语言模型, 它的显著缺点是无法避免的零概率问题, 有时可以通过增大语料库规模来解决, 但是自然语言是一种动态的语言, 所以从概率计算的方法这一角度来解决零概率问题是在目前是比较科学的. 经过实验对于规模较小(语料库规模在3万以内)的语言处理任务, 卡茨回退平滑方法效果就已经很明显, 在接下来的研究中, 我们将重点放在优化与综合利用卡茨回退和Kneser-Ney平滑方法, 利用N-gram模型构建一个提取文章潜在语义的英语作文批改系统.
| 表 9 经过Kneser-Ney后的S2中二元组的频率 |
| [1] |
Jurafsky D, Martin JH. Speech and Language Processing. Pearson International Edition, 2014, 9.
|
| [2] |
Doddington G. Automatic evaluation of machine translation quality using N-gram co-occurrence statics. HLT ’02 Proceeding of the Second International Conference on Human Language Technology Research. 2002. 138–145.
|
| [3] |
Lin CY, Hovy E. Automatic evaluation of summaries using N-gram co-occurrence statics. Proceedings of the 2003 Conference of the North American Chapter of the Association for Computational Linguistics on Human Language Technology - Volume 1 (NAACL’03). 2003. 71–78.
|
| [4] |
Brown PF, deSouza PV, Mercer RL, et al. Computational Linguistics. Cambridge, MA, USA: MIT Press, 1992, 18(4): 467–479. https://dl.acm.org/citation.cfm?id=176313.
|
| [5] |
Cavnar WB, Trenkle JM. N-gram-based text categorization. Proceedings of SDAIR-94, 3rd Annual Symposium on Document Analysis and Information Retrieval. 1994. 161–175.
|
| [6] |
吴军. 数学之美. 北京: 人民邮电出版社, 2012. 28–39.
|
| [7] |
Bird S, Klein E, Loper E. Natural Language Processing with Python. 陈涛, 张旭, 崔杨, 刘海平, 译. 北京: 人民邮电出版社, 2014: 195–197, 221–228.
|
| [8] |
https://en.wikipedia.org/wiki/N-gram.
|
| [9] |
https://en.wikipedia.org/wiki/Katz%27s_back-off_model
|
| [10] |
王晓龙, 关毅. 计算机自然语言处理.北京: 清华大学出版社, 2005: 56.
|
 2018, Vol. 27
2018, Vol. 27



