推荐算法是个性化推荐系统的核心, 其性能直接决定了推荐系统的性能. 在众多的个性化推荐算法中, 协同过滤推荐算法是迄今为止推荐效果最好, 应用最广泛的个性化推荐算法[1,2], 最早在1992年由Goldberg等人提出[3], 主要分为基于用户的协同过滤推荐算法, 基于产品的协同过滤推荐算法和基于模型的协同过滤推荐算法三种. 基于用户的推荐根据用户偏好相似的邻居推荐可能喜欢的产品, 将用户好朋友喜欢的产品推荐给用户; 基于产品的推荐中, 分析用户喜欢过的产品, 根据产品之间的相似度, 找到与用户喜欢的产品相似的产品推荐给用户; 基于模型的推荐中, 根据先验知识构造出分析用户喜好的模型进行推荐. 邓爱林等[4]通过先对用户评分项并集中的空值数据进行预估并填充, 再进行用户间相似性的计算. 张光卫等[5]针对传统相似性度量方法存在的不足, 提出利用云模型在知识层面比较用户相似度的方法, 在用户评分数据稀疏条件下取得较理想的推荐质量. 由于上述的多种优势, 协同过滤算法被电子商务网站普遍采用, Grundy[6]是最早应用的协同过滤推荐系统, 通过建立兴趣模型向用户推荐感兴趣的书籍. 其他典型的推荐系统应用网站还有Amazon、NetFlix和MovieLens[7–9]等.
协同过滤推荐算法在小规模的数据集上的推荐效果良好. 由于实际系统的用户和商品的数据量都十分庞大, 难以及时推荐 [10,11]. 为了提高推荐系统的运行效率, 将聚类算法引入到传统的协同过滤推荐算法中, 缩小了用户或项目的最近邻居搜索范围[12]. 聚类算法将数据对象划分为多个簇, 划分的原则是在不同簇中的对象相似度较低, 在同一簇中的对象相似度较高, 其中典型的聚类算法是K均值算法(K-means), 可以通过对大量用户进行聚类提高运算效率.
但是传统的聚类算法是将数据点分到一个聚类中, 而实际应用中一个数据点可能与多个类中的数据点都有相似之处. 针对这种情况, 将模糊C均值聚类算法应用到推荐系统中, 得到隶属矩阵, 根据样本点关于各个聚类的隶属度, 在隶属度较高的一个或几个聚类中寻找最近邻居, 进行推荐. 该算法与在整个评分矩阵中计算的协同过滤算法相比, 有更好的计算效率, 可以提高算法的可扩展性; 与普通的K-means聚类相比, 解决了硬聚类的问题, 更好得反映了聚类情况, 提高了算法的准确度[13].
随着数据挖掘技术的不断发展, 推荐系统在给人们带来便利的同时, 也存在个人隐私信息泄露的风险. 近年来人们越来越注重个人隐私信息的保护, 不愿意将自己的个人信息提供给数据挖掘平台. 有些人只愿意提供部分信息, 有些人甚至提供虚假信息, 这些行为对数据挖掘的准确性有很大的影响. 怎样实现隐私信息的保护, 消除用户的顾虑, 进而使用户愿意提供完整准确的信息, 成为了数据挖掘平台和用户普遍关注的问题. 差分隐私概念由Dwork提出, 有效解决了上述问题. 之后Agrawal和Strikant提出在噪声干扰后的数据上构造分类树的算法, 在保护隐私信息的同时保证分类的准确性[14]. Sweeney等人提出了k-匿名算法, 对数据进行匿名化处理, 保证任意一条记录与另外的k-1条记录不可区分, 从而保护了隐私数据[15]. Chen等人[16]提出了差分隐私的数据发布机制, Sarathy等人[17]将差分隐私保护方法应用在数值类型的数据上. 彭慧丽[18]等通过将拉普拉斯机制融合到聚类过程中提出了基于差分隐私的社交网络项目推荐方法, 解决了传统匿名化方法过分依赖知识背景的问题. 何明[19]等人通过在协同过滤推荐系统引入满足差分隐私保护的评分矩阵分解机制, 在保证推荐质量的同时保护了用户的隐私信息. 差分隐私是一种基于噪声添加的隐私保护方法, 通过添加满足特定分布的随机噪声使数据失真, 从而达到隐私信息保护的目的.
在保护个人隐私信息的同时, 保证推荐结果的准确度, 对于推荐系统具有十分重要的意义. 本文基于模糊C均值聚类和差分隐私保护实现了基于差分隐私保护的模糊C均值聚类推荐算法, 主要贡献有三点:
(1) 引入模糊C均值聚类算法, 解决硬聚类问题, 提高了算法的准确度.
(2) 通过给模糊C均值聚类过程添加Laplace噪声实现差分隐私保护.
(3) 在MovieLens数据集上进行实验, 验证了本算法的准确度和安全性.
1 基于差分隐私保护的模糊C均值聚类推荐传统聚类算法中一个向量属于一个聚类, 而实际上一个向量可能与多个聚类都有相似之处, 因此只选择一个所属聚类可能会影响推荐结果的准确度. 将模糊C均值聚类算法引入到推荐系统中, 使数据点可以同时属于多个聚类, 从而解决硬聚类问题, 提高推荐准确度. 该算法定义及相关概念描述如下:
定义1. 模糊C均值聚类(Fuzzy C-Means Clustering, FCMC)[20,21]
模糊C均值聚类是用隶属度来表示每个数据点对聚类隶属程度的一种聚类方法. FCMC把n个向量Hi(i=1,2,…,n)分成c个模糊组, 并求每组的聚类中心, 使得非相似性指标的价值函数达到最小.
FCMC使用模糊划分, 隶属度矩阵U允许有取值在0~1之间的元素, 且通过数据归一化, 任一数据到所有聚类的隶属度总和等于1, 表示为式(1):
| $\sum\nolimits_{i = 1}^c {{u_{ij}}} = 1, \forall j = 1, 2, \cdots, n.$ | (1) |
FCMC的价值函数一般化形式如式(2):
| $J\left( {\mathit{{U}}, {\mathit{{H}}_\mathit{{1}}}, \cdots, {\mathit{{H}}_\mathit{{c}}}} \right) = \sum\nolimits_{i = 1}^c {\sum\nolimits_{j = 1}^n {u_{ij}^nd_{ij}^2} } $ | (2) |
其中, uij∈[0,1], Hi为模糊聚类i的聚类中心, dij=||Hi-Xj||为第i个聚类中心与第j个数据点之间的欧氏距离; m∈[0,∞)是一个加权指数. 采用拉格朗日最值法可以求得式(2)达到最小值的必要条件, 构造函数如下:
| $\begin{split}& \widehat J\left( {U, {H_1}, \cdots, {H_c}, {\lambda _1}, \cdots, {\lambda _n}} \right)\\& = J\left( {\mathit{{U}}, {\mathit{{H}}_{\bf{1}}}, \cdots, {\mathit{{H}}_\mathit{{c}}}} \right) + \sum\limits_{j = 1}^n {{\lambda _j}\left( {\sum\limits_{i = 1}^c {{u_{ij}}- 1} } \right)} \\& = \sum\nolimits_{i = 1}^c {\sum\nolimits_{j = 1}^n {u_{ij}^md_{ij}^2} } + \sum\nolimits_{j = 1}^n {{\lambda _j}\left( {\sum\nolimits_{i = 1}^c {{u_{ij}}- 1} } \right)} \end{split}$ | (3) |
其中, λj(j=1,2,…,n)是n个拉格朗日因子. 对所有输入参数求导, 用hi表示Hi的第i个属性, 得到式(2)达到最小时的必要条件为:
| ${h_i} = \sum\limits_{j = 1}^n {u_{ij}^m{x_j}} /\sum\limits_{j = 1}^n {u_{ij}^m} $ | (4) |
| ${u_{ij}} = 1/\sum\limits_{k = 1}^c {{{\left( {\frac{{{d_{ij}}}}{{{d_{kj}}}}} \right)}^{2/\left( {m - 1} \right)}}} $ | (5) |
基于上述两个条件, 模糊C均值聚类算法通过迭代得到聚类中心和隶属矩阵.
为了保护隐私信息, 分析模糊C均值聚类应用于推荐算法中的隐私泄露主要源于两个方面:
(1) FCMC聚类过程中, 假设攻击者获取到每次迭代过程中各聚簇中心点和某个样本点的距离, 就可以通过这些数据推断出该样本点的具体属性值, 而且迭代次数越多, 数据样本属性越少, 其隐私暴露的越彻底.
(2) FCMC聚类过程中, 如果攻击者拥有最大背景知识, 即攻击者已知样本点所属的聚簇内除数据样本点以外的所有数据点和中心点, 就可以根据中心点计算公式推断出这个样本点的属性值.
差分隐私算法是在关键点处添加噪声的隐私保护算法. 拉普拉斯机制是差分隐私保护算法中最简单的算法之一, 较好地解决了数据的准确性和隐私保护之间的平衡问题, 实现了在加入少量噪声的同时达到隐私信息保护的目的[22]. 其定义和相关概念描述如下:
定义2. 差分隐私[22]
给定数据集D和D′, 二者互相之间至多相差一条记录, 即|DΔD′|≤1. 给定一个随机函数k, Range(k)为k的取值范围, pr[Es]为事件Es的披露风险, 若随机函数k提供ε-差分隐私保护, 则对于所有S
| ${\rm{pr}}\left[{k\left( \mathit{{D}} \right) \in \mathit{{S}}} \right] \le {e^{\left( t \right)}} \times {\rm{pr}}\left[{k\left( {\mathit{{D'}}} \right) \in \mathit{{S}}} \right]$ | (6) |
定理1. 全局敏感度[23]
对于函数f: D→Rk, f的敏感度定义为:
| $f = \mathop {\max }\limits_{{\rm{D}}1, {\rm{D}}2} {\left\| {f\left( {{\mathit{{D}}_{\bf{1}}}} \right) - f\left( {{\mathit{{D}}_{\bf{2}}}} \right)} \right\|_1}$ | (7) |
其中, 数据集D1和D2相差至多一个记录, k表示函数f的查询维度. 敏感度只是函数f的性质之一, 与数据集无关.
定理2. Laplace机制[23]
对于任意一个函数f: D→Rd, 其敏感度为Δf, 那么随机化算法A(D)=f(D)+Yd具有ε-差分隐私性, 其中Y~Lap(Δf/ε)为随机噪声, 服从尺度参数为f/ε的Laplace分布.
噪声函数Lap(b)=exp(-|x|/b)呈标准差为√2b的对称指数分布, 其中b=f/ε, 加入的噪声与Δf成正比, 与ε成反比. 因此全局敏感度越大, 加入的噪声也会越大.
通过对以上隐私泄露问题的分析可知, 解决隐私泄露的主要工作是保护聚类中心点. 因此, 在聚类迭代过程中的中心点上添加适当数量的满足差分隐私的Laplace噪声, 在保护隐私的同时保证推荐质量. 基于差分隐私保护的模糊C均值聚类推荐过程描述如下:
(1) 初始化评分矩阵;
(2) 设置参数. 设置聚类的个数为k, 聚类停止条件参数为δ, 根据经验模糊指数m=2, 隶属度阈值为ƞ(0<ƞ<1), 最近邻参数为k, 设置推荐产品评分阈值为Ɵ;
(3) 用0~1的随机数初始化隶属矩阵U, 使其满足公式(1)的归一化条件;
(4) 根据公式(4)计算k个聚类中心d1, d2,…,dk, 对于1≤j≤k, 添加Laplace噪声, dj'=dj+Lap(b), 将其作为初始中心点;
(5) 根据公式(2)计算价值函数Jn(表示第n次迭代), 判断价值函数变化. 如果|Jn-Jn-1|<δ, 停止迭代, 执行(7);否则执行(6);
(6) 根据公式(5)计算新的隶属矩阵U, 执行(4);
(7) 遍历隶属矩阵U, 当用户到聚类的隶属度u>ƞ时, 将用户归为该聚类;
(8) 随机取样本用户, 根据模糊C均值聚类结果, 找到样本用户所属一个或多个聚类, 将所属聚类中的其他用户作为相似用户;
(9) 根据相似用户和样本用户的相似度排序, 得到样本用户的k个最近邻居;
(10)根据最近邻居计算样本用户对产品的评分;
(11)将评分大于Ɵ的产品推荐给样本用户.
上述过程中, 添加的Laplce噪声满足差分隐私条件, 其函数为Lap(b)=exp(–|x|/b), b=f/ε.
基于差分隐私的模糊C均值聚类推荐算法(Differential Privacy protection based Fuzzy C-Means Clustering recommendation, DPFCMC)的实现正如上述算法描述, 在对用户进行模糊C均值聚类过程中通过在聚类中心点添加Laplace噪声实现差分隐私保护, 从而保证了推荐的准确度和安全性.
2 实验系统的设计与实现为了实现基于差分隐私的模糊C均值聚类推荐, 本文设计实现了相应的实验系统, 并进行了相关的测试实验. 实验系统主要在于实现上节提出的推荐算法. 该系统包括3大部分: 数据预处理、推荐模型选取、推荐质量评估. 如图 1所示.
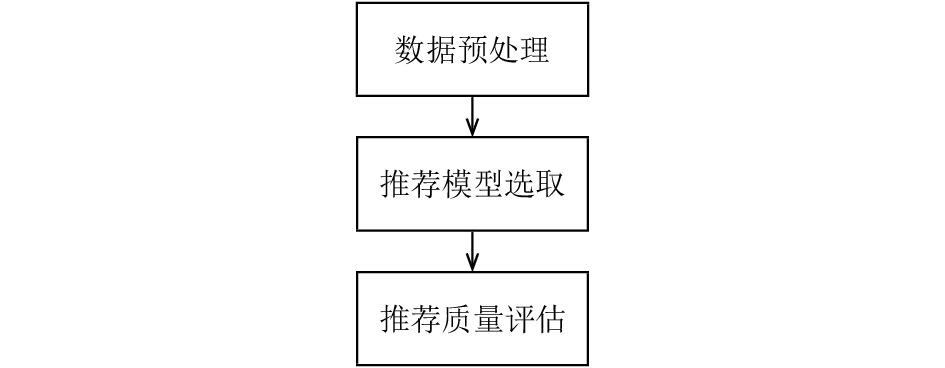
|
图 1 系统结构图 |
(1) 数据预处理模块
该模块根据推荐模型选取模块生成相应推荐模型所需的数据格式, 初始化实验参数. 读取m个用户对n个产品的评分文件, 用这些评分构成m行n列的评分矩阵, 提供给推荐模型.
(2) 推荐模型选取模块
根据(1)提供的数据, 用选取的推荐模型计算被推荐用户对产品的预测评分, 选择预测评分大于某阈值的产品推荐给该用户. 可以选择的模型有本文提出的基于差分隐私保护的模糊C均值聚类推荐模型, 或者其他典型的推荐模型, 如基于K-means聚类的协同过滤推荐模型、基于用户的协同过滤推荐模型等.
(3) 推荐质量评估模块
根据(2)得到的被推荐用户对产品的预测评分, 和该用户对产品的实际评分进行比较, 衡量所用推荐模型的推荐质量. 本实验通过准确度来衡量模型的推荐质量, 评价指标有均方根误差(RMSE), 平均绝对偏差(MAE)和反映召回率和准确率情况的F-measure. 通过计算以上三个评价指标, 来衡量所用推荐模型的推荐质量. 该模块主要为了衡量推荐质量, 通过选取本文提出的新模型和其他典型推荐模型, 分别进行实验, 通过推荐质量的比较, 表现新算法的有效性.
本实验使用Java语言在Myeclipse开发平台上实现以上的各个模块. 我们选择基于差分隐私保护的模糊C均值聚类推荐模型, 其实现流程如图 2所示.
怎样将差分隐私和模糊C均值聚类融合是本实验的关键. 其具体流程如图 3所示. 其核心是根据公式(4)得到聚类中心, 并添加满足差分隐私的Laplace噪声, 根据公式(5)计算隶属矩阵, 不断重复上述过程直到根据公式(2)得到本次迭代和上次迭代的价值函数的绝对差小于某个阈值为止.
实验系统的第三个模块用来验证上述算法的有效性, 主要工作如下:
(1) 选取合适数据集, 验证实验的有效性;
(2) 选取理想评价指标, 衡量推荐准确度;
(3) 为了使本文提出的新算法有比较理想的推荐效果, 通过给相关参数选取不同数值, 对比推荐结果的准确度, 从而选取理想参数;
(4) 为了验证新算法的有效性, 通过给图 1中系统结构的推荐模型选择本文提出的新算法和其他相关典型算法, 分别进行实验, 对比结果.
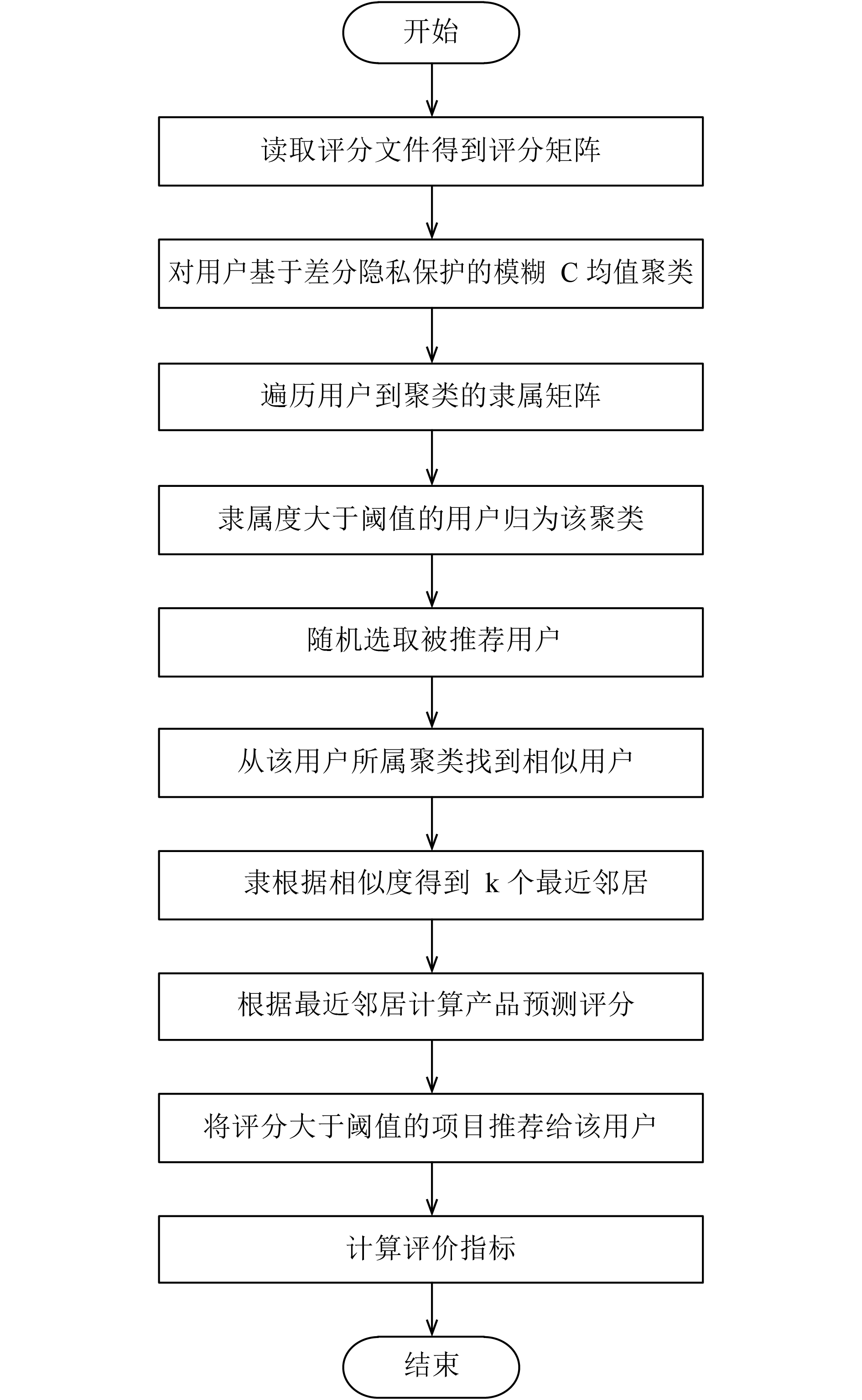
|
图 2 基于差分隐私保护的模糊C均值聚类推荐流程图 |
在以上设计中, 相关典型对比算法的选取是比较关键的问题. 由于本文提出的是基于差分隐私保护的模糊C均值聚类推荐算法, 为了验证模糊C均值聚类对传统硬聚类问题的改善, 设计其与典型的基于用户的K-means聚类推荐算法相比较; 由于新算法是对用户聚类再进行推荐, 为了验证聚类算法的推荐准确度不低于协同过滤算法, 将新算法、基于用户的K-means聚类推荐算法和基于用户的协同过滤推荐算法进行比较.
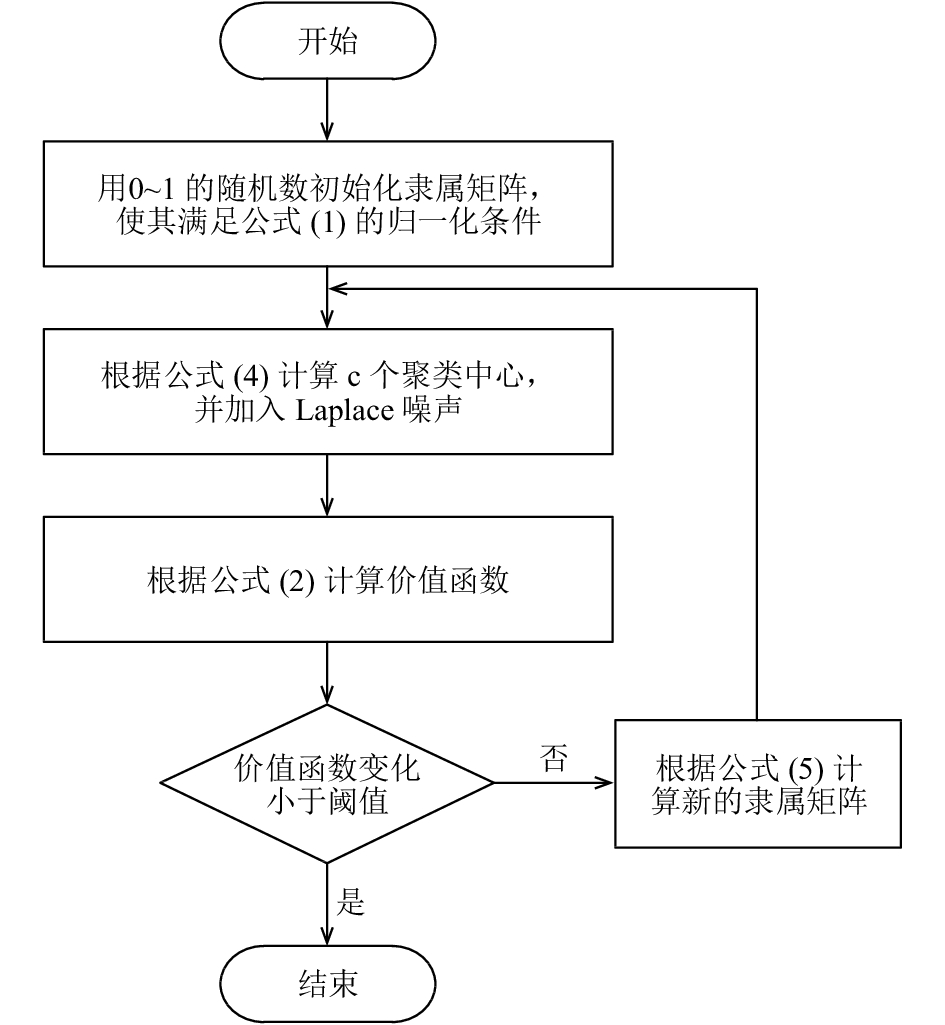
|
图 3 基于差分隐私保护的模糊C均值聚类处理流程 |
3 实验结果与分析 3.1 数据集
实验用到的数据集采用使用的最多的MovieLens数据集. 该数据集是GroupLens Research项目从MovieLens网站上获取的真实数据, 提供的数据量大, 具体真实. 其中, 用户信息主要有: 性别, 年龄, 职业; 电影信息主要有: 电影名称, 电影类别; 评分信息有: 用户id, 电影id, 评分, 评价时间, 用户至少对20部电影评价过, 评分范围为1到5, 数越大代表喜欢程度越高. 本次实验数据采用MovieLens中的100k数据集, 包含943个用户对1682部电影的100 000个评分记录.
3.2 评价指标为了证明存在光流扰动现象, 通过光流检测算法评价推荐系统的标准主要有统计精度度量(prediction error)、决策支持精度度量(IR metrics)和排名度量方法(ranking metrics)三类[4]. 其中统计精度度量方法经常使用的评价指标有均方根误差(RMSE), 平均绝对偏差(MAE); 决策支持精度度量经常使用的评价指标是召回率(recall)和准确率(precision)[24].
假设预测的用户评分集合表示为{p1,p2,…,pN}, 对应的实际用户评分集合为{q1,q2,…,qN}, N代表评分个数.
(1) 均方根误差(RMSE), 越小意味着推荐越准确. 定义为:
| ${{RMSE}} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{\mathit{{p}}_\mathit{{i}}} - {\mathit{{q}}_\mathit{{i}}}} \right)}^2}/N} } $ | (8) |
(2) 平均绝对偏差(MAE)[5]指标通过计算预测的用户评分与实际的户评分之间的偏差度量预测的准确性, 越小意味着推荐越准确, 定义为:
| ${{MAE}} = \sum\limits_{i = 1}^n {\left| {{{{p}}_{{i}}} - {{{q}}_{{i}}}} \right|/N} $ | (9) |
(3) F-measure指标[25]评价推荐的质量, 由召回率和准确率将两者结合组成, 其中召回率反映待推荐项目被推荐的比率, 准确率表示算法推荐成功的比率. F-measure值越大推荐质量越高, 计算公式如下:
| $\begin{array}{l}{{F - measue}} = 2 \times recall \times prescison/recall + presison\end{array}$ | (10) |
为了消除光流扰动效应, 避免在场景中没有运动目标将原始数据集按70%/30%比例随机分为训练数据集与测试数据集, 实验的结果是对所有结果取均值.
为了得到良好的推荐效果, 首先将本文提出的基于差分隐私的模糊C均值聚类推荐算法设置不同参数找到较好的推荐效果. 设置聚类个数范围为10–50, 分析不同聚类个数对推荐质量的影响, 实验结果如图 4; 设置最近邻个数为10–120, 分析不同最近邻个数对推荐质量的影响, 实验结果如图 5.
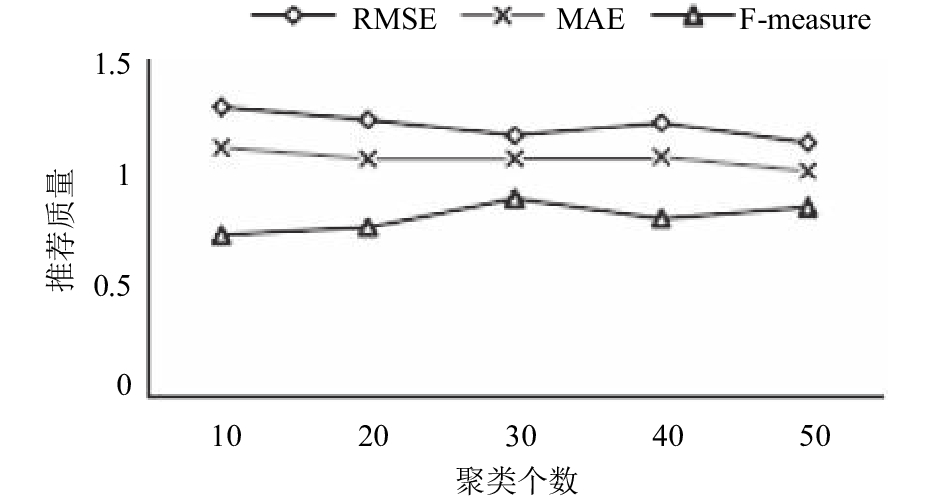
|
图 4 DPFCMC聚类个数对推荐质量的影响 |
根据图 4发现, 本文提出的基于差分隐私的模糊C均值聚类推荐算法在数据集上的聚类个数为30或者50时, RMSE、MAE值相对较小, F-measure值相对较大, 聚类效果较好, 有比较理想的推荐准确度.
|
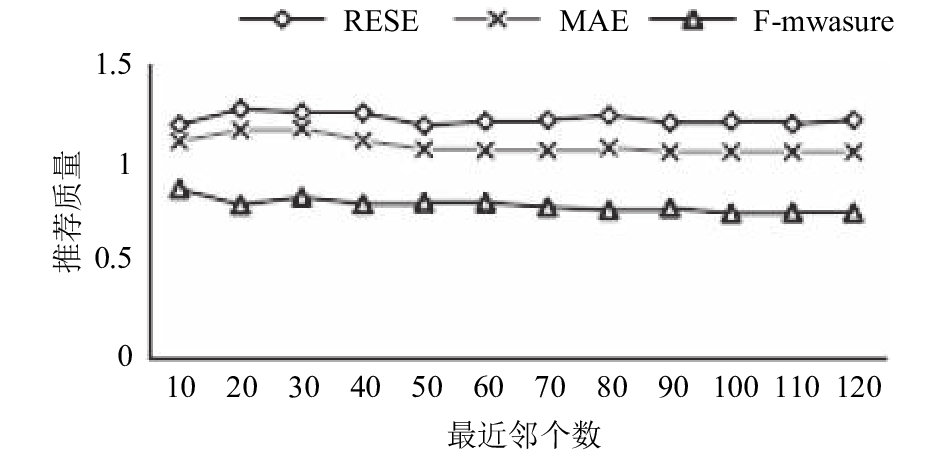
图 5 DPFCMC最近邻个数对推荐质量的影响 |
根据图 5发现, 本文提出的基于差分隐私的模糊C均值聚类推荐算法在数据集上的最近邻个数小于50时RMSE、MAE值相对较大, 同时F-measure值相对也较大; 最近邻个数大于50时, RMSE、MAE值有小幅度的变化, 同时F-measure值有小幅度的减小趋势, 推荐质量没有明显变化趋势. 因此最近邻个数对推荐准确度影响不大.
根据以上试验发现聚类个数为30或50有较好的推荐质量, 最近邻个数对推荐质量没有太明显的影响. 因此在以下实验中, 将本文提出的新算法聚类个数取为30, 分析在最近邻个数为10-100范围内, 本文提出的基于差分隐私的模糊C均值聚类推荐算法(the Differential Privacy protection based Fuzzy C-Means Clustering recommendation, DPFCMC)与基于用户的协同过滤的推荐算法(User-Based Collaborative Filtering, UBCF)、基于K-means聚类的协同过滤推荐算法(Collaborative Filtering based on K-Means clustering, CFKM)的推荐准确度. 通过以上提到的对比实验, 来验证新算法的有效性. 实验结果如图 6, 图 7, 图 8所示, 展示了以上提出的三种算法在RMSE、MAE、F-measure三个评价指标的比较结果.
|
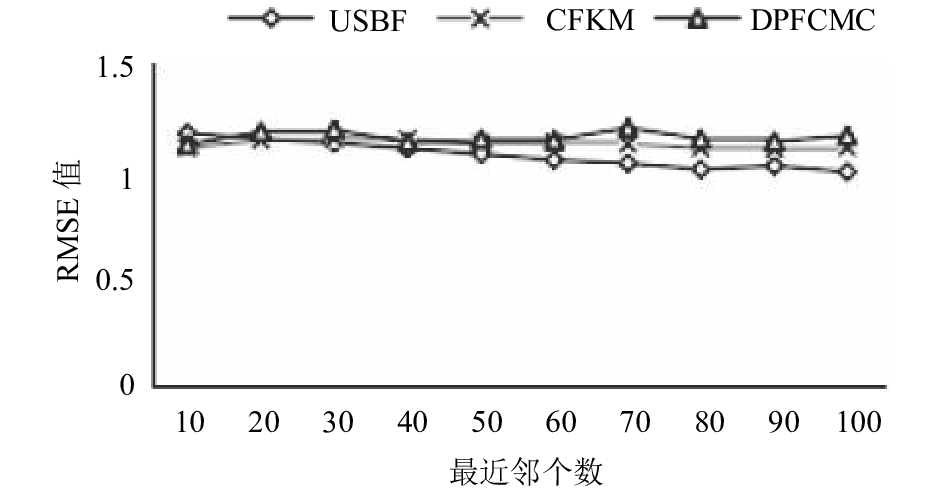
图 6 DPFCMC与其他典型算法的RMSE值对比 |
根据图 6结果可知, 在最近邻个数小于60范围内, 本文提出的基于差分隐私的模糊C均值聚类推荐算法与其他两种算法的RMSE值基本持平; 当最近邻个数大于60, 新算法与基于K-means聚类的协同过滤推荐算法的RMSE值相差不大, 但这两种聚类算法的RSME值都比基于用户的协同过滤推荐算法略大. 因此最近邻个数在一定范围内, 本文提出的新算法与到其他两种算法相比RSME值基本持平, 准确度差距不大.
|
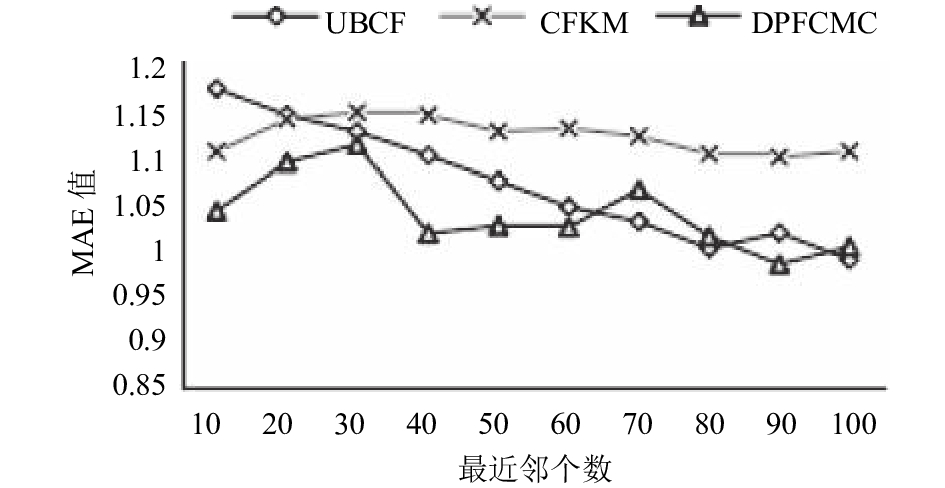
图 7 DPFCMC与其他典型算法的MAE值对比 |
|
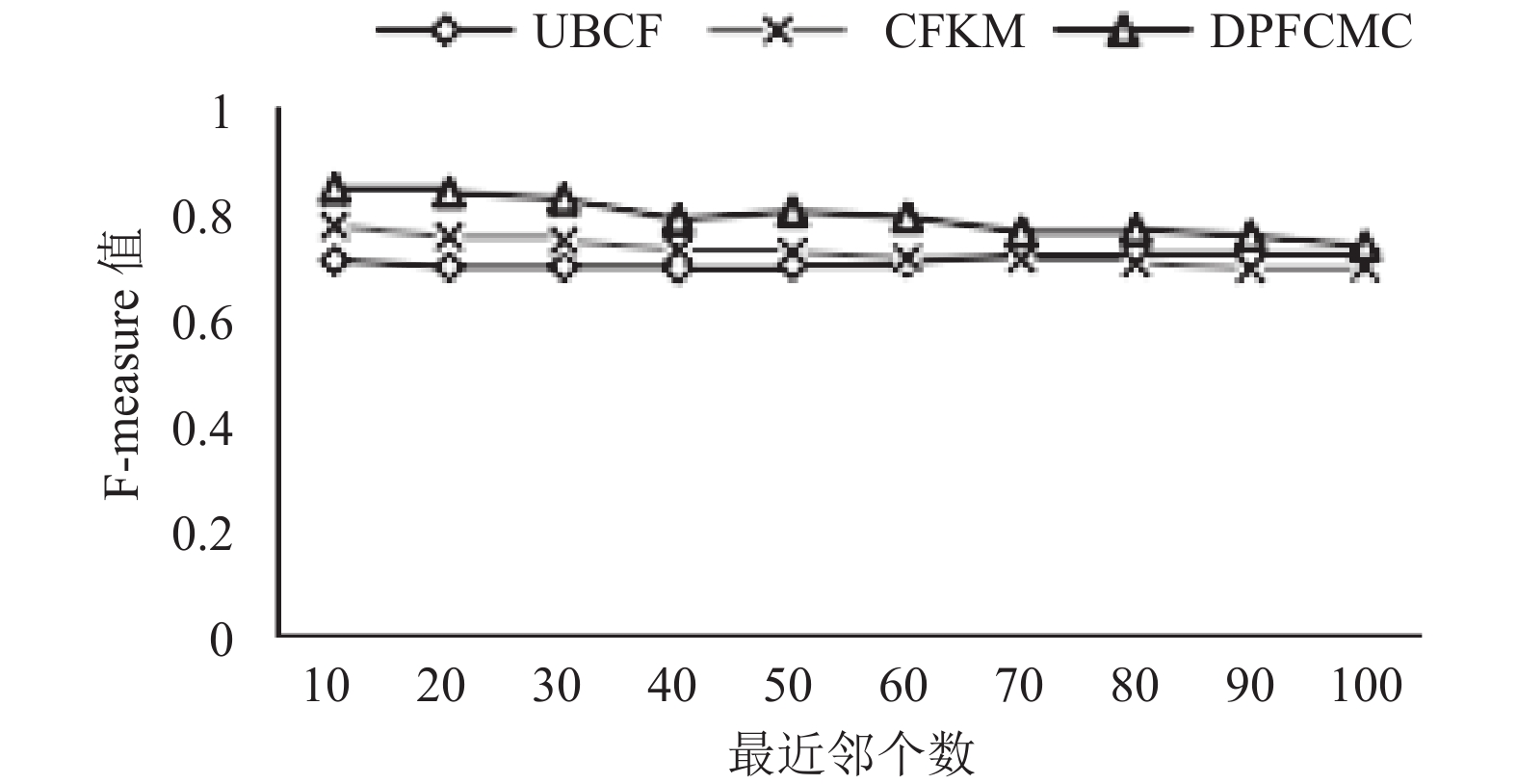
图 8 DPFCMC与其他典型算法的F-measure值对比 |
根据图 7结果可知, 本文提出的基于差分隐私的模糊C均值聚类推荐算法的MAE值大多数比其他两种算法的值小, 有更好的准确度.
根据图 8结果可知, 本文提出的基于差分隐私的模糊C均值聚类推荐算法的F-measure值比其他两种算法都大, 有更好的准确度.
综合以上所有实验结果, 可知本文提出的基于差分隐私的模糊C均值聚类推荐算法的准确度比基于用户的协同过滤的推荐算法和基于K-means聚类的协同过滤推荐算法的准确度更好. 因此, 本文提出的新算法在保护隐私信息的同时保证了更好的准确度.
4 结束语本文将差分隐私保护方法应用到推荐系统中, 并融合模糊C均值聚类, 提出了一种满足差分隐私保护的模糊C均值聚类推荐算法. 通过获得隶属度函数解决传统硬聚类问题, 同时通过添加满足差分隐私保护的Laplace噪声对聚类过程中的聚类中心进行随机干扰. 通过新算法与现有相关典型推荐算法的对比试验证明, 本文提出新的基于差分隐私保护的模糊C均值聚类算法能够在保证一定推荐准确度的同时保护用户的隐私信息, 克服了传统聚类推荐算法中的硬聚类和隐私保护问题. 但在聚类数目和初始中心点的选取方面没有适当的算法进行优化, 在保护隐私信息和保证推荐质量之间难以寻找较理想的平衡, 这些将是之后需要继续深入研究的课题.
| [1] |
Su XY, Khoshgoftaar TM. A survey of collaborative filtering techniques. Advances in Artificial Intelligence, 2009, 2009: 421425.
|
| [2] |
Herlocker JL, Konstan JA, Terveen LG, et al. Evaluating collaborative filtering recommender systems. ACM Transactions on Information Systems, 2004, 22(1): 5-53. |
| [3] |
Goldberg D, Nichols D, Oki BM, et al. Using collaborative filtering to weave an information tapestry. Communications of the ACM, 1992, 35(12): 61-70. DOI:10.1145/138859.138867 |
| [4] |
邓爱林, 朱扬勇, 施伯乐. 基于项目评分预测的协同过滤推荐算法. 软件学报, 2003, 14(9): 1621-1628. |
| [5] |
张光卫, 李德毅, 李鹏, 等. 基于云模型的协同过滤推荐算法. 软件学报, 2007, 18(10): 2403-2411. |
| [6] |
Zhang F, Chang HY. A collaborative filtering algorithm embedded BP network to ameliorate sparsity issue. 2005 International Conference on Machine Learning and Cybernetics. Guangzhou, China. 2005. 1839–1844.
|
| [7] |
Massa P, Avesani P. Trust-aware collaborative filtering for recommender systems. In: Meersman R, Tari Z, eds. On the Move to Meaningful Internet Systems 2004: CoopIS, DOA, and ODBASE. Berlin, Heidelberg. Springer. 2004. 492–508.
|
| [8] |
Konstan JA, Riedl J, Smyth B. Proceedings of the 2007 ACM conference on Recommender systems. ACM Conference on Recommender Systems. Minneapolis, MN, USA. 2007.
|
| [9] |
Chowdhury M, Thomo A, Wadge WW. Trust-based infinitesimals for enhanced collaborative filtering. International Conference on Management of Data. Mysore, India. 2010. 9–12.
|
| [10] |
曾春, 邢春晓, 周立柱. 个性化服务技术综述. 软件学报, 2002, 13(10): 1952-1961. |
| [11] |
Borchers A, Herlocker J, Konstan J, et al. Ganging up on Information Overload. Computer, 1998, 31(4): 106-108. DOI:10.1109/2.666847 |
| [12] |
Kim TH, Park SI, Yang SB. Improving prediction quality in collaborative filtering based on clustering. 2008 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology, 2008. Wi-Iat. Sydney, NSW, Australia. 2008. 704–710.
|
| [13] |
Berget I, Mevik BH, Næs T. New modifications and applications of fuzzy C-means methodology. Computational Statistics & Data Analysis, 2008, 52(5): 2403-2418. |
| [14] |
Agrawal R, Srikant R. Privacy-preserving data mining. Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. New York, NY, USA. 2000. 439–450.
|
| [15] |
Sweeney L. k-Anonymity: A model for protecting privacy. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(5): 557-570. DOI:10.1142/S0218488502001648 |
| [16] |
Chen R, Mohammed N, Fung BCM, et al. Publishing setvalued data via differential privacy. Proceedings of the VLDB Endowment, 2012, 4(4): 1087-1098. |
| [17] |
Sarathy R, Muralidhar K. Some additional insights on applying differential privacy for numeric data. In: Domingo-Ferrer J, Magkos E, eds. Privacy in Statistical Databases. Berlin: Springer, 2010, 210-219. |
| [18] |
彭慧丽, 张啸剑, 金凯忠. 基于差分隐私的社交推荐方法. 计算机科学, 2017, 44(S1): 395-398, 423. |
| [19] |
何明, 常盟盟, 吴小飞. 一种基于差分隐私保护的协同过滤推荐方法. 计算机研究与发展, 2017, 54(7): 1439-1451. |
| [20] |
Li X, Lu X, Tian J, et al. Application of fuzzy c-means clustering in data analysis of metabolomics. Analytical Chemistry, 2009, 81(11): 4468-4468. DOI:10.1021/ac900353t |
| [21] |
Dembélé D, Kastner P. Fuzzy C-means method for clustering microarray data. Bioinformatics, 2003, 19(8): 973-980. DOI:10.1093/bioinformatics/btg119 |
| [22] |
Dwork C. Differential privacy: A survey of results. In: Agrawal M, Du D, Duan Z, et al, eds. Theory and Applications of Models of Computation. Berlin: Springer-Verlag, 2008. 1–19.
|
| [23] |
Dwork C, Mcsherry F, Nissim K, et al. Calibrating noise to sensitivity in private data analysis. Halevi S, Rabin T. Theory of Cryptography. Berlin: Springer-Verlag, 2006. 265–284.
|
| [24] |
马宏伟, 张光卫, 李鹏. 协同过滤推荐算法综述. 小型微型计算机系统, 2009, 30(7): 1282-1288. |
| [25] |
Goldberg K, Roeder T, Gupta D, et al. Eigentaste: A constant time collaborative filtering algorithm. Information Retrieval, 2001, 4(2): 133-151. DOI:10.1023/A:1011419012209 |
 2018, Vol. 27
2018, Vol. 27


