2. 福建省特种设备检验研究院, 福州 350008;
3. 福建师范大学 数学与信息学院, 福州 350007;
4. 数字福建环境监测物联网实验室, 福州 350007;
5. 福州大学 物理与信息工程学院, 福州 350108
2. Fujian Special Equipment Inspection and Research Institute, Fuzhou 350008, China;
3. College of Mathematics and Informatics, Fujian Normal University, Fuzhou 350007, China;
4. Digit Fujian Internet-of-Things Laboratory of Environmental Monitoring, Fujian Normal University. 350007, China;
5. College of Physics and Information Engineering, Fuzhou University, Fuzhou 350108, China
电梯作为现代人类活动最后50米的交通工具, 已成为与城市居民生活密切相关的重要基础设施之一. 过去十年间, 国内电梯保有量迅速增加, 到2016年已达到493.69万台[1]. 电梯的构成要素多, 事故的发生既有一定的随机性和突发性, 又有一些必然性, 仅2016年国内就发生电梯事故48起, 死亡41人[2]; 据统计, 电梯构成要素中发生的事故概率分别为: 厅门事故占80%左右, 井道内事故占15%左右, 其他占5%; 引发事故的原因主要有设备缺陷、作业违章、管理缺陷[3].
目前, 电梯的安全主要靠定期维护或年检的方式, 维保公司依据规程对电梯的各构成要素进行固定项目的检修[4,5], 虽然且该方式存在“过修”或者“欠修”的情况[6], 对可能发生的异常难以检测, 但在过去10年间它为我国万台电梯事故率由1.56起降至0.15起发挥了重要作用[7].
但随着电梯保有量的持续增长, 电梯使用频率的快速提高, 影响电梯安全运行的隐患随之进一步加大, 传统管理方式面临巨大挑战. 毫无疑问, 将电梯联网实现监管已成为该行业重要举措, 如在上海地区, 将新一代电梯运行状态安全监控系统铺开, 到2018年预增至10万台以上[8]. 2016年, 《质检总局2016年电梯安全攻坚战工作方案》首次明确要求运用大数据、物联网技术, 多措并举以提升电梯应急能力和监管效能[9].
国内已有专家围绕电梯安全积极探索评价方法. 庆光蔚等选取与电梯安全相关的指标并计算权重, 通过模糊综合评价法评估电梯安全, 模糊综合评价方法能够较为准确的反映和衡量电梯运行情况及安全性能, 指出群体性电梯管理提升点, 指标体系的建立仍有待完善, 缺乏动态检测、评估[10]. 陈国华等分析电梯历史故障信息, 采用基于故障率修正的模糊综合评价方法评估电梯系统风险, 在模糊评估过程中引入故障率修正系数, 故障率修正系数的引入有利于实现电梯系统风险动态评价[11], 该方法具有较好的适应性, 能够随电梯安全技术、安全管理水平修正评价系数, 但评估因素的权重需要不同专业领域的专家依据问卷调查表进行主观评分, 主观性强. 李刚通过故障原因分析, 研究整机性能与各部件间的关系建立电梯安全评价数学模型, 提出了针对长期服役电梯的安全评价项目、内容、要求及流程, 为长期服役电梯部件及整机报废、维修、改造提供了技术支撑, 有利于长期服役电梯安全管理及安全水平的提升, 但评价程序的智能化程度差, 仅能根据输入进行风险值的计算, 无法实现逻辑算法较为复杂的部件及整机判废[12]. 这些研究方法为电梯故障分析、监管、改进等方面提出了建设性建议, 但如何将事后评估变为对电梯的实时评估, 快速实现对电梯健康状态预警, 特别是减少评估过程的人为主观性和加快评估过程, 无疑是一项具有挑战性的研究.
毫无疑问, 大数据的出现为各个行业带来了巨大变化[13], 它可以更有效地表征数据、解释数据[14]. 电梯的物联网发展已积累了海量的数据, 如何应用新的智能技术, 例如Logistic回归等适用于大数据的人工智能算法, 发挥这些数据的作用, 挖掘电梯健康状况与运行数据间的关联性, 针对运行中电梯进行健康评估并预警、减少评估时间, 无疑是一项很有意义的研究.
1 评估模型方案设计电梯设备健康评估, 涉及到实时数据(物联网技术监控电梯运行数据)、静态数据(设备的型号、厂商等)、维保数据和历史运行数据, 如图1所示, 时间跨度长、数据量大, 且电梯设备健康需及时评估, 因此需要一种运算时间短, 适用于大数据的评估算法.
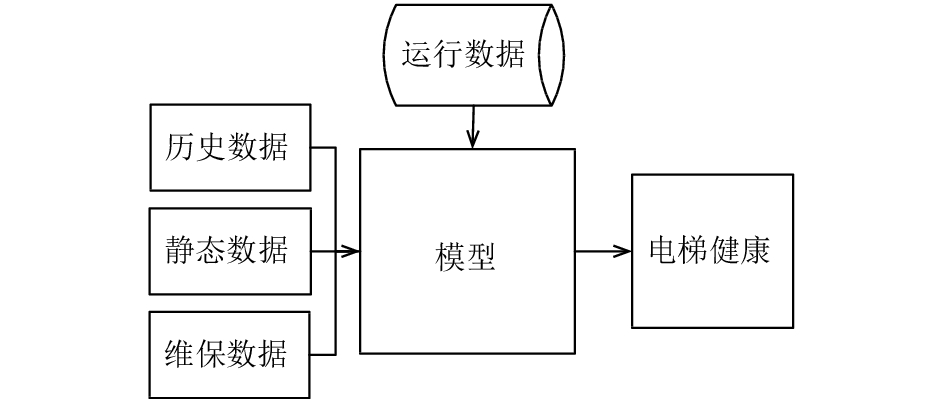
|
图 1 电梯设备的健康评估数据组成框图 |
Logistic回归模型作为一种有效的数据处理方法在很多领域都有广泛的应用[15–18], 是公认的最常用数据科学研究方法[19]. 方案最后选定Logistic回归模型作为最终方案, 一方面由于Logistic回归假定数据服从二项式分布, 电梯数据量大, 符合二项分布的基础条件, 另一方面, Logistic回归利用统计学手段, 对数据进行预测分析, 提供后验概率, 相对于传统机器学习或深度学习算法其运算速度快, 在数据量较大时效果优异, 适用于大数据环境下电梯健康评估.
评价方案主要包括数据清洗、特征筛选、特征处理、模型训练和设备评估等, 如图2.
2 特征筛选与规整 2.1 特征筛选电梯健康运行需要每部分有机协调, 缺一不可. 从功能上看, 电梯可划分成六部分[12]. 结合目前的相关研究[4,5,10,12,20]结果, 选取相关的整体特征和局部特征. 整体特征是评价电梯各部分共同包含的特征, 局部特征是根据各部分的特点筛选的特有特征. 筛选发现, 现有条件无法针对对重系统、导向系统、轿厢系统筛选出适宜的局部特征, 如图3.

|
图 2 设备健康评估方案流程 |
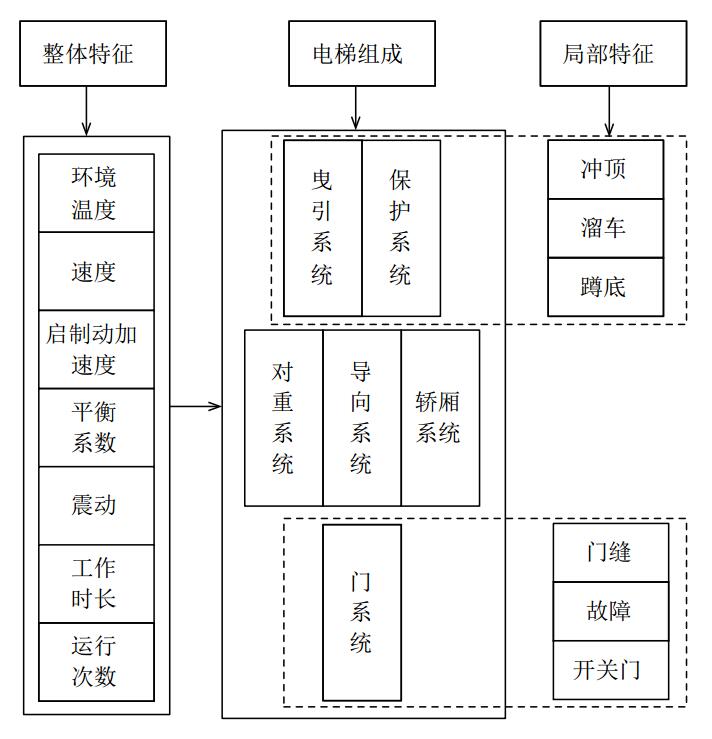
|
图 3 电梯健康评价特征 |
2.2 特征预处理
电梯特征原始数据不符合评估模型要求, 因此需要借助数据清洗、预处理等方法使其符合要求, 结果如表1、表2.
3 模型优化电梯健康评估是评估模型根据电梯运行数据得出的结果, 因此评估模型是整个系统核心. 优化评估模型, 是提高评估系统泛化能力最关键的步骤.
3.1 样本均衡化机器学习分类方法对平衡数据集分类取得了良好的效果, 但对于基于总体分类精度为学习目标的分类器而言, 样本不均衡势必会导致分类器过多关注多数类样本, 从而使少数类样本分类性能下降[21,22].
| 表 1 电梯整体特征处理后参数 |
| 表 2 电梯局部特征处理后参数 |
样本数据库中包括发生故障电梯和正常运行电梯的数据, 但正常运行电梯的样本量远大于故障电梯样的数据量, 所有在训练分类前需要解决样本不均衡问题. 同时, 由于故障样本数据量级不大, 所以在解决样本不均衡的前提下需要合理利用样本. SMOTE算法根据已有的样本生成新样本点, 扩大样本个数[23]. 但SMOTE可能引入新的噪声, 使用SMOTE过采样算法结合KMeans++聚类降采样, 既避免了为样本集引入较多的噪声, 又有效地解决了训练集样本稀疏的问题[24,25].
3.2 数据标准化Logistic回归通过拟合系数, 建立评价模型. 但样本指标单位不一致、不同的量纲, 影响训练模型参数, 降低模型泛化能力. 数据的标准化将数据约束到同一标尺,降低了单位与量纲对模型的影响[26,27].
标准分数(Z-score)是一种常见的标准化法, 将数值变准化到Z分数, 公式如下:
| $z = \left( {x - \mu } \right)/\sigma $ |
模型通过标准分数法将不同单位的数据, 统一到同一尺度, 降低了属性间的关联度, 同时压缩了数据中的噪声, 提高了模型泛化能力.
在电梯评价模型中, 需要对所有的特征数据进行标准化处理. 模型训练时, 每个特征的所有训练数据计算“平均值”和“方差”, 后根据公式对数据进行标准化处理. 在评估中, 所有数据的标准化参数, 使用训练模型中“平均值”和“方差”参数带入公式中进行标准化.
3.3 高阶线性模型结合本文的需要, 先对相关原理进行分析. Logistic回归将预测值映射到“Sigmod”函数上并将预测值转化成预测概率, 函数形式为:
| $y = \frac{1}{{1 + {e^{ - {w^{\rm{T}}}x}}}}$ |
在二分类问题中, 定义属于“1”的概率表示为
| $P(y|x,\theta ) = f{(x)^{{y}}}{(1 - f(x))^{(1 - y)}}$ | (1) |
对式(1)求最大似然估计可解得参数
| $P(y = 1|x,w) = \frac{{{e^{{w^{\rm{T}}}x}}}}{{1 + {e^{{w^{\rm{T}}}x}}}}$ |
| $P(y = 0|x,w) = \frac{1}{{1 + {e^{{w^{\rm{T}}}x}}}}$ |
求解的关键在于求解参数
线性回归通过学习、计算, 拟合出结果与特征参数间的线性数量关系:
| $p({\varepsilon _i}) = \frac{1}{{\sqrt {2\pi } \sigma }}\exp ( - \frac{{{{({\varepsilon _i})}^2}}}{{2{\sigma ^2}}})$ |
根据极大似然估计法可得:
| $L(w) = \prod\limits_{i = 1}^m {p({y_i}|{x_i};w)} $ |
| $L(w){\rm{ = }}m\log \frac{1}{{\sqrt {2\pi } \sigma }} - \frac{1}{{{\sigma ^2}}}.\frac{1}{2}\sum\limits_{i = 1}^m {{{(f({x_i}) - {y_i})}^2}} $ |
若使得式
| $J(w) = \frac{1}{2}\sum\limits_{i = 1}^m {{{(f({x_i}) - {y_i})}^2}} $ | (2) |
Logistic回归的本质是线性回归, 线性回归是变量的一阶形式, 一阶模型对样本的学习不充分. 将
| $\begin{aligned}f(x) = & {w_0} + {w_1}{x_1} + {w_2}{x_1}^2 + {w_3}{x_1}^3 +\cdots+ \\ & {w_{l - 2}}{x_n} + {w_{l - 1}}{x_n}^2 + {w_l}{x_n}^3\cdots\end{aligned}$ |
在变量设计上将
求解式(1)的最大似然估计时, 解得的
| $\left\{\begin{array}{l}f(w) = \frac{1}{2}\sum\limits_{i = 1}^N {[{y_i}{\rm{ - }}f({x_i},w)} {]^2} + \lambda \sum\limits_i^N {{{[{w_i}]}^2}} \\\text{即}:\min (f(w))\end{array}\right.$ | (3) |
但在数学推导上仍旧无法推算
交叉验证将原始数据进行分组, 一部分作为训练集, 另一部分作为验证集. 首先用训练集对模型进行训练, 再将相关参数回带入目标函数选择适合的参数. 通过交叉验证法, 如图4, 利用测试数据以式(3)损失函数为评价标准, 选取合适的
电梯健康评估系统主要包括离线模型训练和电梯设备实时评估两个部分.
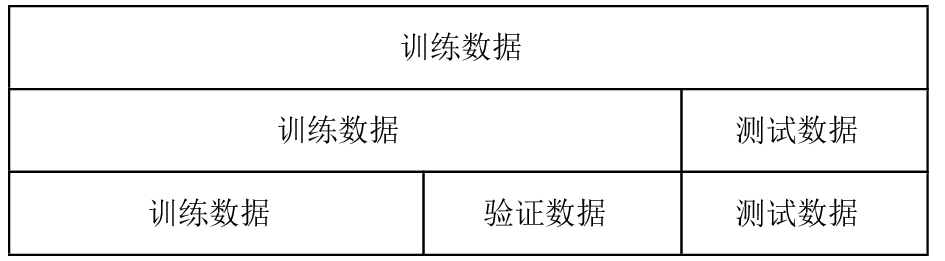
|
图 4 交叉验证 |
离线模型训练部分包括, 使用离线数据, 借助统计算法, 数据的规整, 预处理等方法整理原始数据, 利用整理后的数据学习训练logistic回归模型关键参数, 建立评价模型.
实时评估系统将实时上传的数据整合后放入训练后的模型, 达到对电梯健康实时评估、预警, 如图5.

|
图 5 电梯健康评估系统 |
评估模型计算每部分发生故障的概率

|
图 6 评估结果 |
5 结束与展望
电梯是一个复杂系统, 具有构成要素多、供应商多, 生命周期长等特点; 从安装、维保到维修, 影响其运行状态的要素很多. 本文从电梯组成、影响或可以用于评价电梯健康因素入手, 选取评价参数. 借助现象与故障之间的联系, 在历史数据的基础上建立数学模型, 利用现有数据, 使用大数据分析方法建立评估模型. 引入数据预处理、惩罚因子、交叉验证方法, 针对实际业务优化评估模型. 该模型评估时间周期短, 模型动态调整, 达到了对电梯健康实时监控并预警.
评估阶段取平均值作为电梯最后评价结果, 但电梯各部分对电梯重要并不对等, 因此评价电梯各部分的比重系数可作为下阶段的研究重点.
在整个研究设计过程中, 由于缺乏统一的规范和标准, 各厂商的数据获取难度大, 信息孤岛现象还比较严重. 随着物联网技术的发展, 应尽快实施电梯物联网的协议和接口标准化, 加快提升行业的活力和发展态势.
| [1] |
中国产业信息网. 2017年中国电梯产量、保有量及行业发展趋势. http://www.chyxx.com/industry/201705/520639.html. [2017-05-09/2017-10-16].
|
| [2] |
新浪网. 电梯夺命敲响警钟超八成因检修保养不到位. http://news.sina.com.cn/sf/news/ajjj/2017-02-08/doc-ifyaexzn9229269.shtml, 2017-02-08/2017-10-16.
|
| [3] |
郭雯雯. 电梯事故分析及监督检验对策. 质量技术监督研究, 2006(8): 102-104. |
| [4] |
中华人民共和国国家质量监督检验检疫总局. TSG T7001-2009 电梯监督检验和定期检验规则-曳引与强制驱动电梯. 2009.
|
| [5] |
中华人民共和国国家质量监督检验检疫总局. TSG T5001-2009 电梯使用管理与日常维护保养规则. 2009.
|
| [6] |
万林, 朱叶盛. 基于人工神经网络和证据理论的电梯健康状态评估. 工业控制计算机, 2016, 29(7): 44-45. DOI:10.3969/j.issn.1001-182X.2016.07.019 |
| [7] |
张绪鹏, 刘增莉, 陈亮. 电梯物联网安全监测关键点研究. 中国安全生产, 2015, 10(3): 64-65. |
| [8] |
新浪网.上海启用" 智能电梯”物联网2018年入网10万台. http://news.dichan.sina.com.cn/2015/02/28/1323239.html. [2015-02-28/2017-10-26].
|
| [9] |
国家质量监督检验检疫总局.质检总局2016年电梯安全攻坚战工作方案. http://www.aqsiq.gov.cn/xxgk_13386/ywxx/tzsb/201604/t20160401_463767.htm. [2015-06-04/2017-10-26].
|
| [10] |
庆光蔚, 王会方, 胡静波. 电梯安全级别模糊综合评价方法及应用研究. 中国安全生产科学技术, 2013, 9(4): 129-134. |
| [11] |
陈国华, 李刚, 王新华,等. 基于故障率修正的电梯系统风险模糊综合评价研究. 中国安全科学学报, 2014, 24(2): 59-64. |
| [12] |
李刚. 长期服役电梯安全评价技术及方法研究[硕士学位论文]. 广州: 华南理工大学, 2014.
|
| [13] |
赵玲玲, 刘杰, 王伟. 基于Spark的流程化机器学习分析方法. 计算机系统应用, 2016, 25(12): 162-168. |
| [14] |
程学旗, 靳小龙, 王元卓,等. 大数据系统和分析技术综述. 软件学报, 2014(9): 1889-1908. |
| [15] |
李航. 统计学习方法. 北京: 清华大学出版社, 2012: 78–80
|
| [16] |
余建农, 覃庆玲, 胡俊. 银行信息系统项目后评估模型与评分卡设计研究. 华中师范大学学报(自然科学版), 2016, 50(6): 867-874. |
| [17] |
姜盛. 基于Logistic的信用卡套现侦测评分模型. 计算机应用, 2009, 29(11): 3088-3091, 3095. |
| [18] |
张婷婷, 景英川. 个人信用评分的Adaptive Lasso-Logistic回归分析. 数学的实践与认识, 2016, 46(18): 92-99. |
| [19] |
kaggle. The State of Data Science & Machine Learning. https://www.kaggle.com/surveys/2017. [2017-11-13].
|
| [20] |
李立京.电梯综合测试系统与故障诊断技术的研究[博士学位论文]. 天津: 天津大学, 2002.
|
| [21] |
陶新民, 郝思媛, 张冬雪,等. 不均衡数据分类算法的综. 重庆邮电大学学报(自然科学版), 2013, 25(1): 101-110, 121. |
| [22] |
赵永彬, 陈硕, 刘明,等. 基于置信度代价敏感的支持向量机不均衡数据学. 计算机工程, 2015, 41(10): 177-180, 185. DOI:10.3969/j.issn.1000-3428.2015.10.033 |
| [23] |
Chawla NV, Bowyer KW, Hall LO, et al. SMOTE: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357. |
| [24] |
Maroulas V, Mike J, Marchese A. K−means clustering on the space of persistence diagrams. Wavelets and Sparsity XVII. 2017. 29.
|
| [25] |
林舒杨, 李翠华, 江弋,等. 不平衡数据的降采样方法研究. 计算机研究与发展, 2011, 48(s3): 47-53. |
| [26] |
孙红卫, 吕春燕, 祁爱琴,等. 综合评价中数据标准化的原理研究. 中国卫生统计, 2015, 32(2): 342-344, 349. |
| [27] |
方洪鹰. 数据挖掘中数据预处理的方法研究[硕士学位论文]. 重庆: 西南大学, 2009.
|
| [28] |
周志华. 机器学习. 北京: 清华大学出版社, 2016: 53–63.
|
| [29] |
李琳娜, 杨炳儒, 周法国. 基于高阶逻辑的复杂结构归纳学习研究. 计算机科学, 2008, 35(9): 136-143. DOI:10.3969/j.issn.1002-137X.2008.09.036 |
| [30] |
赵谦, 孟德宇, 徐宗本. L1/2正则化Logistic回归
. 模式识别与人工智能, 2012, 25(5): 721-728. DOI:10.3969/j.issn.1003-6059.2012.05.001 |
 2018, Vol. 27
2018, Vol. 27


