伙伴算法是一种动态存储分配算法, 用于实现操作系统内核空间和用户空间(如C语言库)的分配和回收操作. Knowlton[1]和Knuth[2]最早系统地描述了用于内存管理中的二分伙伴算法. 之后, Hirschberg[3]和Shen[4]先后提出斐波那契伙伴算法和加权伙伴算法, 作为伙伴算法的两种变体. 为了适应不同的内存请求概率分布, Peterson[5]又进一步提出泛化伙伴算法, 针对不同请求概率分布采取不同的分配策略.
实现伙伴算法的内存管理模块称为伙伴系统, 是固定分区和可变分区的一个合理折中方案[6]. 然而, 由于存在内碎片和外碎片的问题, 以及无法支持虚拟存储器的缘故, 在现代操作系统内核中单纯的伙伴系统并没有得到广泛应用, 而分页机制则成为内存管理的主流技术. 尽管如此, Linux内核成功地将分页机制与伙伴系统系统结合起来, 分页机制将逻辑地址空间映射到物理地址空间, 伙伴系统负责在物理地址空间中分配和回收页框, 因而内存块的尺寸被限定为页框尺寸的倍数. 为了追求时间效率, Linux内核选择实现了二分伙伴算法, 该算法的优点在于伙伴地址的计算更加简便、高效.
目前, 涉及Linux内核伙伴系统分析的文献很多, 其中以Bovet[7]和Gorman[8]的著作最具代表性. 但此类文献都侧重源代码的分析, 涉及众多的实现细节, 很难突出伙伴系统的核心部分, 而且也缺乏能够演示算法过程的相关的实例. 此外, 在Linux内核伙伴算法的实现中, 如何确定一个内存块伙伴的索引, 以及在完成合并之后如何确定内存块的首页索引, 是理解该算法的关键所在. 上述文献仅描述了解决这两个问题的计算方法, 但并未对其正确性给出严格的证明.
本文旨在结合实例, 在更加抽象的层面详细分析Linux内核所实现伙伴系统的关键数据结构和算法, 并针对上述两个关键计算方法, 给出相应的证明. 第2节描述伙伴系统的主要数据结构. 第3节分析伙伴系统的分配算法. 第4节首先证明与索引计算相关的几条结论, 然后分析伙伴系统的回收算法.
2 数据结构 2.1 物理内存的三级管理结构Linux内核将物理内存管理对象分为节点、区和页框三个层次. 早期的内核仅支持单处理器系统, 而现在的Linux内核则可以在包括多处理器系统在内的各类体系结构的计算机上运行. 为了适应NUMA体系结构中处理器拥有各自本地内存节点(即分布式内存)的情况, 内核采用节点描述符存储内存节点的相关信息. 每个物理内存节点对应一个节点描述符, 其中包含相应内存节点的标识符、起始页框号、页框数等字段. 单处理器系统和对称多处理器系统属于UMA体系结构, 这类系统仅包含一个内存节点, 因而内核仅为其分配唯一的节点描述符.
依据内存节点寻址特点及用途的不同可将每个内存节点进一步划分为若干个内存区. 例如, 在IA32系统中, 唯一的内存结点被分为DMA, NORMAL和HIGHMEM三个区. 内核为每个内存区分配一个区描述符, 其中包含内存区的名称、起始页框号、页框数等字段.
物理内存是一个线性地址空间, 即使在NUMA系统中, 所有内存节点也是统一编址. 页框是物理内存管理的基本单位, 如果以页框作为元素, 整个物理内存就可以视为一个页框数组, 而物理内存管理的主要工作就是从这个数组中分配和回收页框. 内核为每个页框分配一个页描述符, 用于记录对应页框的信息.
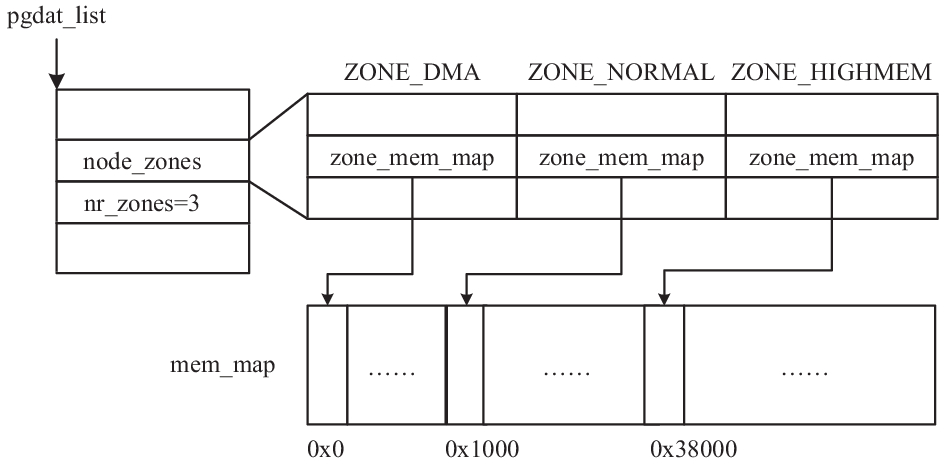
节点描述符、区描述符和页描述符构成物理内存管理的基本数据结构, 这些结构被相互关联并组织在一起. 所有页描述符被存储在全局数组mem_map中, 区描述符中用zone_mem_map指针指向对应内存区起始页框的页描述符, 而内存节点所含内存区的区描述符则存储在node_zones字段中, 该字段是一个区描述符数组, 区描述符的数量存储在nr_zones字段中. 所有节点描述符被链接成一个链表, 全局变量pgdat_list指针指向第一个节点描述符. 图1演示了一个典型的IA32系统中各描述符之间的关系.
|
图 1 物理内存管理三级数据结构 |
图1中, pgdat_list指针指向系统唯一的内存节点描述符, 该描述符的node_zones数组中包含三个区描述符, 每个区描述符的zone_mem_map字段指向相应内存区起始页框的页描述符, 系统中所有页描述符存储在全局数组mem_map中.
2.2 伙伴系统的数据结构伙伴系统从指定的内存区中分配页框, 使用完毕后页框被回收到其所属的内存区. 为了满足不同尺寸的需要, 内存区中的页框被组合成一些内存块, 每个内存块包含2k个连续的页框, 其中k称为内存块的阶, 阶为k的内存块称为k阶内存块. MAX_ORDER宏定义了阶数的上限, 默认为11, 即阶的取值范围是0~10, 因此内存块的尺寸最小为4 K, 最大为4 M. 对于一个内存块, 它的第一个页框称为首页, 其余页框称为尾页. 一个内存块的第一个页框的描述符称为首页描述符. 内存区的第一个页框在区内的相对索引称为该内存块的首页索引, 一个k阶内存块的首页索引必须被2k整除.
未分配内存块处于空闲状态, 为了便于分配和回收, 所有空闲内存块被链接到其阶数对应的空闲链表中. 区描述符中的free_area数组用于跟踪空闲内存块, 该数组包含MAX_ORDER个元素, 每个元素的下标即阶数. 数组元素是free_area结构体, 包含free_list和nr_free两个字段. 其中, free_list字段是空闲链表的头节点, 用于链接对应阶数第一个空闲内存块的首页描述符, nr_free字段记录空闲链表长度, 即相应阶数的空闲内存块数. 页描述符的lru字段链接同阶下一个空闲内存块的首页描述符.
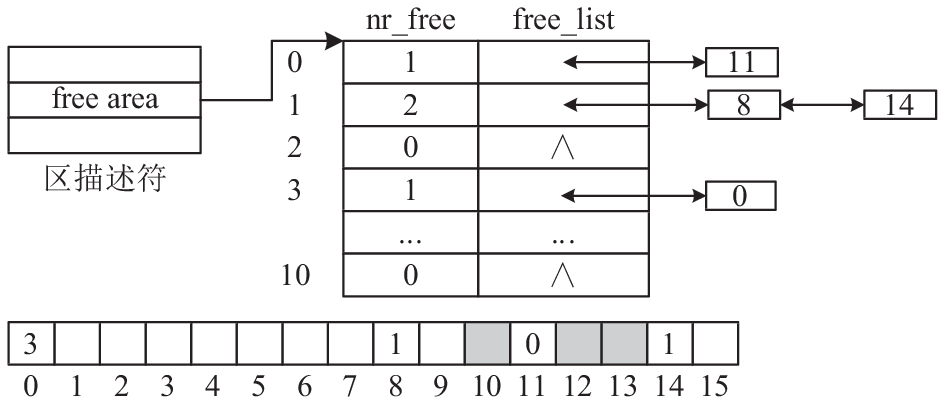
图2上方展示一个包含16个页框的内存区的空闲链表. 在区描述符的free_area数组中, 0阶、1阶和3阶空闲链表中分别链接一些空闲内存块的首页描述符. 其中, 0阶空闲链表中包含一个内存块的首页描述符, 首页索引为11; 1阶空闲链表中包含两个内存块的首页描述符, 首页索引分别为8和14. 3阶空闲链表中包含一个内存块的首页描述符, 首页索引为0.
|
图 2 空闲链表与内存块分布图示例 |
图2下方展示该内存区中的页描述符数组. 其中白色方块代表空闲页框描述符, 标注数字的白色方块代表空闲内存块的首页描述符, 其中的数字表示该内存块的阶数, 灰色方块代表已分配的页框描述符.
页框状态存放在页描述符的private和flags两个字段中. 其中, private字段用于存放内存块的阶数, 该字段仅在空闲内存块的首页描述符中有效. flags字段包含一个PG_Private标志位, 用于指示private字段的取值是否有效. PG_Private为1表示页框是空闲内存块的首页, 其中的private字段取值有效; 否则, 表示页框已分配或属于空闲内存块的尾页, 其中的private字段取值无效. 在图2的页描述符数组中, 灰色方块和未标注数字的白色方块代表的页描述符的PG_Private标志为0, 标注数字的白色方块代表的首页描述符的PG_Private标志为1.
3 分配算法 3.1 分配算法描述当内核请求分配内存时, 伙伴系统执行分配算法以满足其需求. 分配算法的基本思想是寻找能够满足内核需求的最小空闲内存块, 如果该内存块的阶大于内核请求的阶, 则将其逐步划分为一系列低阶内存块, 直到划分出恰好满足需求的一个内存块, 并分配给内核使用. 其余低阶内存块按其所属的阶被依次插入相应的空闲链表, 用于满足今后的内存请求.
假设内核需要从内存区zone分配一块order阶空闲内存块, 分配算法从order阶开始遍历zone内存区的free_area数组, 查找能够满足需求的空闲内存块. 如果order阶的空闲链表非空, 则说明至少存在一个恰好满足需求的内存块, 此时查找成功. 否则, 逐阶递增查找每一个高阶空闲链表, 直至成功找到空闲链表非空的一个阶. 如果直到MAX_ORDER-1阶也未能找到, 则查找失败, 说明无法满足内核提出的内存分配请求, 此时返回空指针, 表示内存分配失败.
若查找成功, 将找到的阶记为current. 从current阶空闲链表移除第一个空闲内存块的首页描述符, 用page指针指向它, 并计算free_area[current].nr_free--. 如果current>order, 则说明该内存块大于请求的内存块, 因而需要对其进行划分. 这里将其等分为两个current-1阶的空闲内存块, 位于低地址端的一块记为BL, 其页描述符由page指针指向; 位于高地址端的一块记为BH, 其页描述符由page+2current-1指针指向. 将BH插入current-1阶空闲链表, 并计算free_area[current-1].nr_free++. 然后, 通过page+2current-1指针修改BH的页描述符, 将flags.PG_Private置位, 为private赋值current-1. 如果current-1仍然大于order, 则需要对BL进行类似的划分, 直到剩余内存块的阶恰好等于order. 此时, page指针指向剩余内存块的首页描述符, 将其flags. PG_Private清零, 表示该内存块已被分配. 最后, 将zone的页框数free_pages减2order, 这样就成功完成了内存块的分配工作.
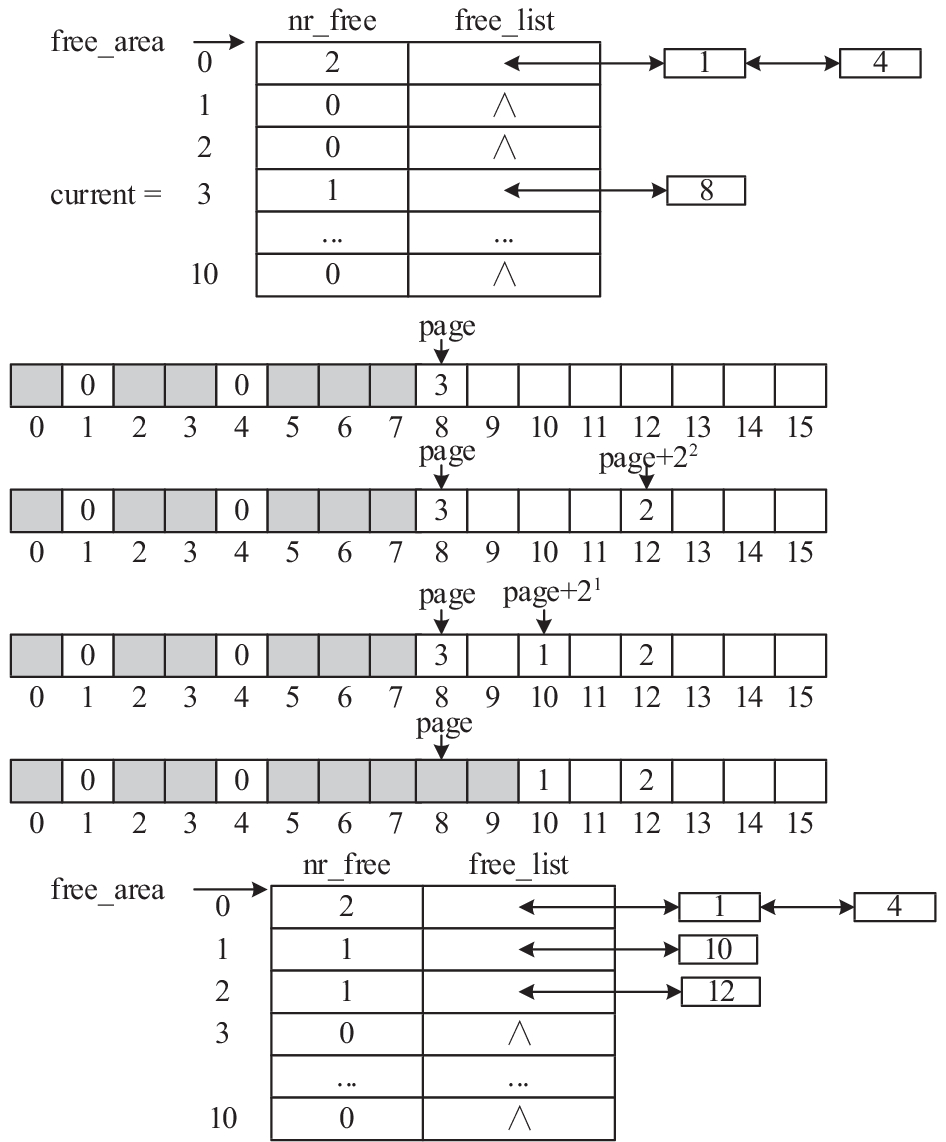
3.2 分配算法实例下面结合实例说明分配算法的执行过程. 假设内存区zone包含16个页框, 如图3上方空闲链表所示, zone当前存在两个0阶和一个3阶空闲内存块. 图2中间演示了内存分配过程. 假设内核请求分配一个1阶空闲内存块, 对于free_area数组的查找将从1阶开始. 由于1阶的空闲链表为空, 因此继续查找高阶空闲链表, 直到发现3阶空闲链表非空, 查找结果current取值为3, 这说明存在一个3阶的空闲内存块可供分配. 然后, 从3阶空闲链表移除第一个内存块(首页索引为8)的首页描述符, 并用page指针指向它, 同时计算free_area[3].nr_free--.
|
图 3 内存块的分配过程示例 |
由于找到的空闲内存块的尺寸(3阶)超过了内核请求的尺寸(1阶), 因此需要划分. 首先将其等分为两个2阶内存块, 其中高地址端一块的首页描述符指针为page+22, 其首页索引为12. 在描述符中将flags.PG_Private置位, private赋值为2. 同时将描述符插入2阶空闲链表, 并计算free_area[2].nr_free++. 然后, 进一步划分低地址端的另一个2阶内存块, 将其等分为两个1阶内存块. 高地址端一块的首页描述符指针为page+21, 首页索引为10. 在其描述符中将flags.PG_Private置位, private赋值为1. 然后, 将页描述符插入1阶空闲链表, 并计算free_area[1].nr_free++. 剩下低地址端的一块1阶内存块恰好满足内核的需求, 因此停止划分. 此时, page指针指向剩余内存块的首页描述符, 将其flags. PG_Private清零, 再将zone的页框数free_pages减21, 最后返回page指针, 至此内存分配成功. 图2下方展示分配成功后的空闲链表.
4 回收算法 4.1 伙伴的概念及性质伙伴系统回收算法的基本思想是首先确定待回收内存块的伙伴, 如果伙伴是空闲的, 则将二者合并为一个高阶空闲内存块. 重复上述合并过程, 直至伙伴不再空闲或合并形成的空闲内存块达到最高阶. 在上述过程中, 每次合并前都要将伙伴从其所在的空闲链表中移除. 合并完成后, 最终形成的高阶空闲内存块被插入相应空闲链表的表头. 不难看出, 回收算法的一项重要的工作是确定待回收内存块的伙伴, 因此在描述回收算法之前, 首先需要明确伙伴的含义.
定义. 两个内存块互为伙伴(Buddy)当且仅当满足以下三个条件: (1) 二者在内存中相邻且不重叠; (2) 二者具有相同的阶; (3) 假设二者的阶都为k, 则合并后形成一个k+1阶空闲内存块, 该内存块的首页索引恰好能够被2k+1整除.
此外, 为了高效地完成回收工作, 还需要解决下列两个关键问题: (1) 如何确定伙伴内存块? (2) 如何确定合并后形成的高阶内存块的首页? 下列几条结论可以帮助解决这两个问题.
定理1. 假设待回收内存块B的阶为k, 其首页索引为p, 其伙伴的首页索引为b, 则有下式成立:
| $b = p \oplus {2^k}$ | (1) |
证明: 根据伙伴应满足的条件(1)和条件(2)可知, B内存块的伙伴只可能是与其相邻的两个k阶内存块, 下面分两种情况讨论:
(1) 如果伙伴在右边, 则
(2) 如果伙伴在左边, 则
综合上述两种情况, p[k]的取值决定了B的伙伴: 若p[k]=0, 则伙伴是B右边相邻的k阶内存块, 否则伙伴是B左边相邻的k阶内存块. 又由于p与2k做异或运算相当于对p[k]求反, 故当p[k]=0时, 有:
| $b{\rm{ = }}p + {2^k} = p \oplus {2^k}$ | (2) |
当p[k]=1时, 有:
| $b{\rm{ = }}p - {2^k} = p \oplus {2^k}$ | (3) |
由(2)、(3)两式可知式(1)成立.
推论. p与b的二进制形式中除了p[k]与b[k]是相反的, 其余各位完全相同.
定理2. 假设待回收内存块B的阶为k, 其首页索引为p, 其伙伴的首页索引为b, B与其伙伴合并后形成的k+1阶内存块B'的首页索引为:
| ${p'} = p \wedge b$ | (4) |
证明: 分两种情况讨论:
(1) 若伙伴在B的右边, 则p[k]=0, 因此有:
| $p \wedge b = p$ | (5) |
成立. 此时, B'的首页即B的首页, 故:
| ${p'} = p$ | (6) |
由(5)、(6)两式可知(4)式成立.
(2) 若伙伴在B的左边, 则p[k]=1, 因此有:
| $p \wedge b = b$ | (7) |
成立. 此时, B'的首页即B的首页, 故:
| ${p'} = b$ | (8) |
由(7)、(8)两式可知(4)式成立.
4.2 回收算法描述完成上述准备工作后, 下面讨论回收算法. 假设内核请求伙伴系统回收属于zone内存区的一个order阶内存块B, page指针指向B的首页描述符. 首先用page-base计算出B的首页索引, 记为p, 其中base是zone内存区的起始页描述符指针. 然后将p代入式(1)计算出伙伴的首页索引, 记为b, 伙伴的首页描述符指针为base+b. 如果描述符的flags.PG_Private为0则说明伙伴已经被分配, 因此无法与B合并. 否则, 将B与其伙伴合并.
合并时首先从order阶空闲链表中移除B的伙伴, 同时计算free_area[order].nr_free--, 然后将伙伴页描述符中的flags.PG_Private清零, 从而完成两个内存块的合并, 形成一个order+1阶的空闲内存块B1. 然后, 将p和b代入式(4)计算出B1的首页索引p(被替换为新值, 因此p始终是当前合并内存块的首页索引). 如果B1的伙伴空闲则再次合并形成order+2阶的空闲内存块B2, 该过程一直持续下去, 直到伙伴不再空闲, 或者合并获得的空闲内存块达到最高阶, 合并过程结束. 此时, p是最终合并获得空闲内存块B’的首页索引, B’的阶数记为order’.
接下来还需要进行一些数据结构的修改操作. 首先, base+p是B’的首页描述符指针, 通过该指针将描述符的flags.PG_Private置位, private赋值为order’. 然后, 将B’的首页描述符插入order’阶的空闲链表, 并计算free_area[order’].nr_free++. 最后, 为zone内存区的空闲页数加2order’.
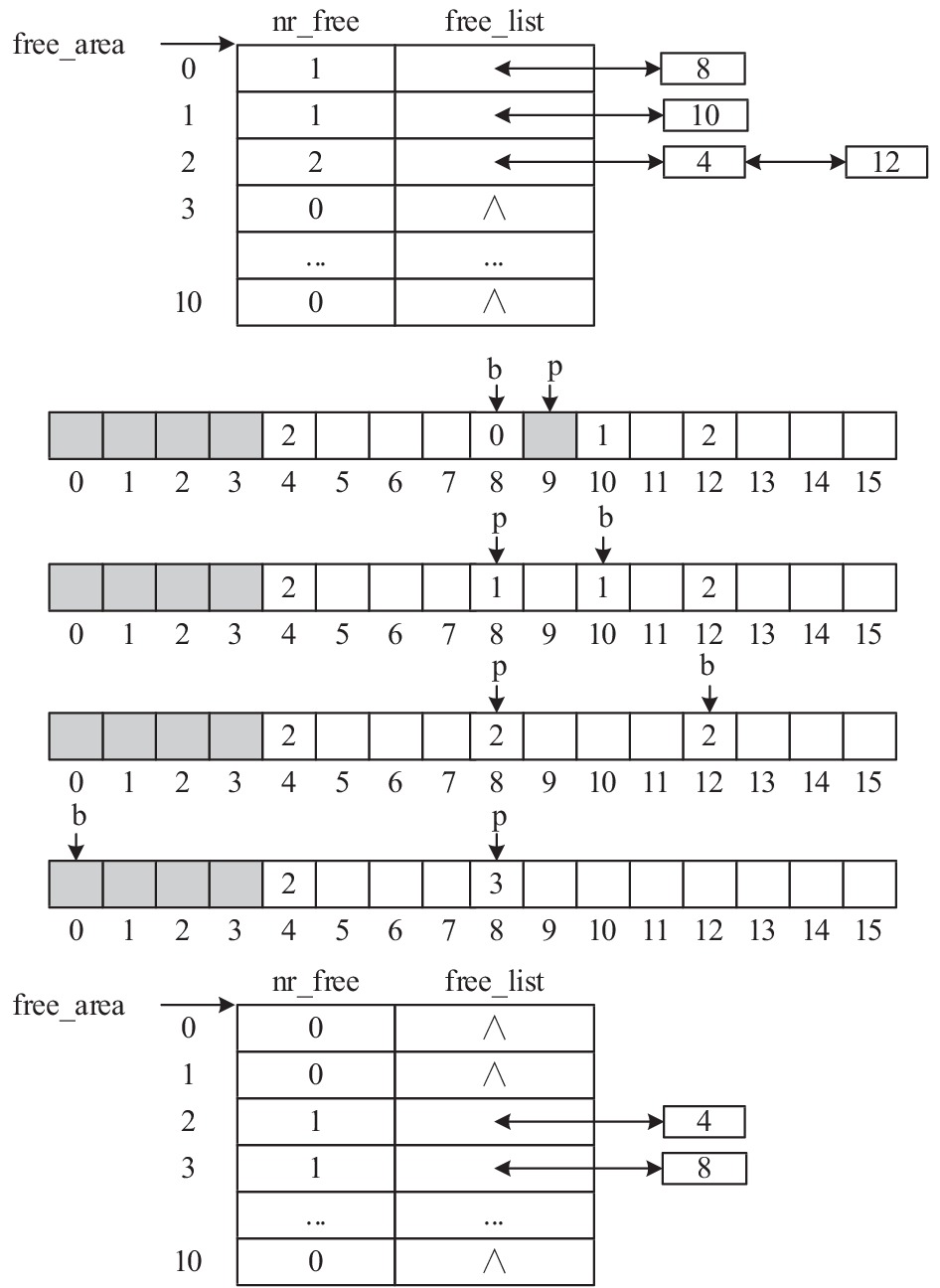
4.3 回收算法实例下面结合实例说明回收算法的执行过程. 假设内存区zone包含16个页框, 如图4上方空闲链表所示, zone当前存在一个0阶、一个1阶和两个3阶空闲内存块. 图4中间演示了内存块的回收过程.
|
图 4 内存块的回收过程示例 |
假设内核需要回收一块0阶内存块, 其首页索引p为9. 由式(1)计算出该内存块伙伴的首页索引b为8, 然后从0阶空闲链表中移除伙伴的首页描述符, 其flags.PG_Private为1, 表明伙伴是空闲的. 将两个内存块合并后形成一个1阶空闲内存块, 由式(2)计算出该内存块的首页索引p为8.
表1概括了合并内存块的三次迭代所涉及的伙伴, 及合并内存块首页索引的计算过程. 其中, 第一行对应上面描述的第一次迭代, 后两行对应后续两次迭代. 最后一行表示第三次迭代后, 合并形成一个3阶空闲内存块, 其首页索引为8, 伙伴的首页索引为0, 由于伙伴首页描述符的flags.PG_Private为0, 因而不再空闲, 合并过程结束.
| 表 1 回收过程中伙伴和合并内存块索引的计算 |
合并完成后, 修改合并形成的3阶空闲内存块的首页描述符, 将flags.PG_Private置位, private赋值为3. 然后, 将描述符插入3阶的空闲链表, 并计算free_area[3].nr_free++. 最后, 为zone内存区的空闲页数加20. 图4下方展示回收成功后的空闲链表.
5 结论本文以Linux内核源代码为基础, 对负责物理内存分配和回收的伙伴系统进行了详细的分析, 通过对源代码的抽象, 突出了伙伴系统的关键数据结构和算法. 此外, 本文着重分析伙伴索引以及合并内存块首页索引的计算方法, 给出了论证算法正确性的相关证明.
物理内存管理是Linux内核的底层机制, 其分配和回收算法的性能会显著影响操作系统的整体性能. 伙伴算法是一种简洁、高效的存储管理算法, Linux内核对该算法的实现代码也非常简短、优雅. 尽管如此, Linux内核的伙伴系统仍然存在优化的空间. 本文的研究内容有助于深入理解伙伴系统的实现思想, 这为进一步优化算法的研究奠定了基础.
| [1] |
Knowlton KC. A fast storage allocator. Communications of the ACM, 1965, 8(10): 623-625. DOI:10.1145/365628.365655 |
| [2] |
唐纳德•E. 克努特. 计算机程序设计艺术-第1卷: 基本算法. 苏运霖, 译. 3版. 北京: 国防工业出版社, 2002: 415–417.
|
| [3] |
Hirschberg DS. A class of dynamic memory allocation algorithms. Communications of the ACM, 1973, 16(10): 615-618. DOI:10.1145/362375.362392 |
| [4] |
Shen KK, Peterson JL. A weighted buddy method for dynamic storage allocation. Communications of the ACM, 1974, 17(10): 558-562. DOI:10.1145/355620.361164 |
| [5] |
Peterson JL, Norman TA. Buddy systems. Communications of the ACM, 1977, 20(6): 421-431. DOI:10.1145/359605.359626 |
| [6] |
Stallings W. 操作系统——精髓与设计原理. 陈向群, 陈渝, 译. 7版. 北京: 电子工业出版社, 2012: 225–226.
|
| [7] |
Bovet DP, Cesati M. Understanding the linux kernel. 3rd ed. O'Reilly Media, 2005: 311–316.
|
| [8] |
Gorman M. Understanding the linux virtual memory manager. Upper Saddle River, New Jersey, USA: Prentice Hall, 2004: 105–110.
|
 2018, Vol. 27
2018, Vol. 27

