采油速度是衡量油田开发速度和产能的关键指标, 其大小是油藏的年产量与地质储量的比值, 是油田开发过程中必不可少的生产指标. 储层构造特征和物性特征、流体性质、井网部署情况、国家政策以及油价都会对采油速度产生影响[1]. 采油速度过低会增加生产成本, 采油速度过高可能会导致含水快速上升、驱油效率下降, 因此, 确定油田合理的采油速度对油田高效开发意义重大. 目前计算合理采油速度的常用方法主要有静态影响因素分析法、动态影响因素分析法、数值模拟法、类比法、线性回归法、多元逐步回归法和数理统计等[2,3], 这些预测方法多是以公式的形式进行表述. 文献[4]利用含水率分流方程, 建立了采油速度与油藏特征、含水率、含水饱和度及含水上升速度等影响因素的关系表达式, 但预测效果受限于参与拟合数据的质量. 支持向量回归机是建立在统计学习理论基础上的学习算法, 与神经网络等算法相比具有更好的性能[5], 但实际应用中样本数据含有多源异构信息, 采用单一核函数无法发现数据中隐含的复杂规律, 进而准确地描述数据的内在特性, 增强决策函数的可理解性[6]. 已有理论研究及应用表明, 多个核函数的优化组合代替单个核函数能增强决策函数的可解释性, 并能使支持向量回归机获取更优的性能[7,8]. 本文提出基于改进灰狼算法优化多核支持向量回归机模型, 并将其应用到采油速度预测. 首先应用灰色关联分析理论利用实际地质数据和开发数据对采油速度影响因素进行重要性分析, 然后利用历史数据来训练构建的支持向量回归机模型来完成预测, 使得预测模型既考虑动静态数据, 又能自适应历史数据, 克服了历史拟合数据质量对已有采油速度预测算法的影响, 具有很好泛化能力和推广前景.
1 多核支持向量回归机原理支持向量回归机通过核函数的隐式映射将数据映射到高维特征空间, 完成样本训练和数据预测. 设X是输入空间, H是更高维度空间, 存在一个映射
| $\begin{gathered} \mathop {\min }\limits_{w,b,\xi ,\zeta } \frac{1}{2}{\left\| w \right\|^{\rm{2}}} + C\sum\limits_{i = 1}^l {\left( {\mathop \xi \nolimits_i + \mathop \zeta \nolimits_i } \right)} \\ {\rm {s.t.}}\left\{ \begin{array}{l} \mathop y\nolimits_i - w*\varphi ({x_i}) - b \le \varsigma + \mathop \xi \nolimits_i \\ w*\varphi ({x_i}) + b - \mathop y\nolimits_i \le \varsigma + \mathop \zeta \nolimits_i \\ \mathop \zeta \nolimits_i ,\mathop \xi \nolimits_i \ge 0,i = 1,2,\cdots,l \\ \end{array} \right. \\ \end{gathered} $ | (1) |
| $\begin{split} & L\left( {w,b,\varsigma ,\xi ,\zeta ,\mathop \alpha \nolimits^* ,\alpha ,\mathop \beta \nolimits^* ,\beta } \right) = \dfrac{1}{2}{\left\| \omega \right\|^{\rm{2}}}{\rm{ + }}C\sum\limits_{i = 1}^l {\left( {\mathop \xi \nolimits_i + \mathop \zeta \nolimits_i } \right)} \\ & - \sum\limits_{i = 1}^l {\mathop \alpha \nolimits_i^* } \left( {\varsigma + \mathop \xi \nolimits_i - \mathop y\nolimits_i + w*\varphi (\mathop x\nolimits_i ) + b} \right) \\ & -\sum\limits_{i = 1}^l {\mathop \alpha \nolimits_i } \left( {\varsigma + \mathop \zeta \nolimits_i + \mathop y\nolimits_i - w*\varphi (\mathop x\nolimits_i ) - b} \right) - \sum\limits_{i = 1}^l {\mathop \beta \nolimits_i^* } *\mathop \xi \nolimits_i - \sum\limits_{i = 1}^l {\mathop \beta \nolimits_i *\mathop \zeta \nolimits_i } \\ & {\rm {s.t.}}\;\mathop \alpha \nolimits_i^* ,\mathop \alpha \nolimits_i ,\mathop \beta \nolimits_i^* ,\mathop \beta \nolimits_i \ge 0,i = 1,2,\cdots,l \\ \end{split} $ | (2) |
其中
则式(1)可转化为:
| $\left\{ \begin{gathered} \mathop {\min }\limits_{w,b,\xi ,\zeta } \mathop {\max }\limits_{\mathop \alpha \nolimits^* ,\alpha ,\mathop \beta \nolimits^* ,\beta } L(w,b,\mathop \alpha \nolimits^* ,\alpha ,\mathop \beta \nolimits^* ,\beta ) \\ {\rm {s.t.}}\;\mathop \alpha \nolimits_i^* ,\mathop \alpha \nolimits_i ,\mathop \beta \nolimits_i^* ,\mathop \beta \nolimits_i \ge 0,i = 1,2,\cdots,l \\ \end{gathered} \right.$ | (3) |
式(3)经过拉格朗日对偶可得:
| $\left\{ \begin{gathered} \mathop {\max }\limits_{\mathop \alpha \nolimits^* ,\alpha ,\mathop \beta \nolimits^* ,\beta } \mathop {\min }\limits_{w,b,\xi ,\zeta } L(w,b,\mathop \alpha \nolimits^* ,\alpha ,\mathop \beta \nolimits^* ,\beta ) \\ {\rm {s.t.}}\;\mathop \alpha \nolimits_i^* ,\mathop \alpha \nolimits_i ,\mathop \beta \nolimits_i^* ,\mathop \beta \nolimits_i \ge 0,i = 1,2,\cdots,l \\ \end{gathered} \right.$ | (4) |
将式(2)对
| $\mathop {\min }\limits_{w,b,\xi ,\zeta } L(w,b,\mathop \alpha \nolimits^* ,\alpha ,\mathop \beta \nolimits^* ,\beta ) = - \dfrac{1}{2}\sum\limits_{i,j = 1}^l {\left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} \left( {\mathop \alpha \nolimits_j^* - \mathop \alpha \nolimits_j } \right)\varphi (\mathop x\nolimits_i )\varphi \left( {\mathop x\nolimits_j } \right) - \varsigma \sum\limits_{i = 1}^l {\left( {\mathop \alpha \nolimits_i^* + \mathop \alpha \nolimits_i } \right)} + \sum\limits_{i = 1}^l {\mathop y\nolimits_i \left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} $ | (5) |
将式(5)带入式(4)可得:
| $\left\{ \begin{array}{l} \mathop {\max }\limits_{\mathop \alpha \nolimits^* ,\alpha } - \dfrac{1}{2}\displaystyle\sum\limits_{i,j = 1}^l {\left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} \left( {\mathop \alpha \nolimits_j^* - \mathop \alpha \nolimits_j } \right)\varphi (\mathop x\nolimits_i )\varphi \left( {\mathop x\nolimits_j } \right) - \varsigma \displaystyle\sum\limits_{i = 1}^l {\left( {\mathop \alpha \nolimits_i^* + \mathop \alpha \nolimits_i } \right)} + \displaystyle\sum\limits_{i = 1}^l {\mathop y\nolimits_i \left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} \\ {\rm {s.t.}}\;\mathop {0 \le \alpha }\nolimits_i^* ,\mathop \alpha \nolimits_i \le C,\displaystyle\sum\limits_{i = 1}^l {\left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right) = 0} ,i = 1,2,\cdots,l \\ \end{array} \right.$ | (6) |
将式(6)转化为最小值优化可得:
| $\begin{split} & \mathop {\min }\limits_{\mathop \alpha \nolimits^* ,\alpha } \left\{ {\dfrac{1}{2}\sum\limits_{i,j = 1}^l {\left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} \left( {\mathop \alpha \nolimits_j^* - \mathop \alpha \nolimits_j } \right)\varphi (\mathop x\nolimits_i )\varphi \left( {\mathop x\nolimits_j } \right) + \varsigma \sum\limits_{i = 1}^l {\left( {\mathop \alpha \nolimits_i^* + \mathop \alpha \nolimits_i } \right)} - \sum\limits_{i = 1}^l {\mathop y\nolimits_i \left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} } \right\} \\ & {\rm {s.t.}}\;\left\{ \begin{array}{l} 0 \le \alpha _i^*,{\alpha _i} \le C \\ \displaystyle\sum\limits_{i = 1}^l {(\alpha _i^* - \alpha _i^{}) = 0,i = 1,2,\cdots,l} \\ \end{array} \right. \\ \end{split} $ | (7) |
令核函数
| $\left\{ \begin{array}{l} \mathop {\min }\limits_{\mathop \alpha \nolimits^* ,\alpha } \dfrac{1}{2}\displaystyle\sum\limits_{i,j = 1}^l {\left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} \left( {\mathop \alpha \nolimits_j^* - \mathop \alpha \nolimits_j } \right)k\left( {\mathop x\nolimits_i ,\mathop x\nolimits_j } \right) + \varsigma \displaystyle\sum\limits_{i = 1}^l {\left( {\mathop \alpha \nolimits_i^* + \mathop \alpha \nolimits_i } \right) - \displaystyle\sum\limits_{i = 1}^l {\mathop y\nolimits_i \left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} } \\ {\rm {s.t.}}\;\mathop {0 \le \alpha }\nolimits_i^* ,\mathop \alpha \nolimits_i \le C,\displaystyle\sum\limits_{i = 1}^l {\left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right) = 0} ,i = 1,2,\cdots,l \\ \end{array} \right.$ | (8) |
预测函数为:
| $f\left( x \right) = \sum\limits_{i = 0}^l {\left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} k({x_i},x) + b$ | (9) |
由对称半正定矩阵的性质可得:
| $K({x_i},{x_j}) = \lambda \mathop K\nolimits_{\rm {Poly}} ({x_i},{x_j}) + (1 - \lambda )\mathop K\nolimits_{\rm {RBF}} ({x_i},{x_j}){\rm{ = }}\lambda {\left( {\gamma x_i^{\rm T}{x_j} + r} \right)^d} + (1 - \lambda )\left( {\exp \left( { - \gamma {\left\| {{x_i} - {x_j}} \right\|^2}} \right)} \right)$ | (10) |
因此多核支持向量机的目标函数为:
| $\left\{ \begin{array}{l} \mathop {\min }\limits_{\mathop \alpha \nolimits^* ,\alpha } \dfrac{1}{2}\displaystyle\sum\limits_{i,j = 1}^l {\left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} \left( {\mathop \alpha \nolimits_j^* - \mathop \alpha \nolimits_j } \right)K\left( {\mathop x\nolimits_{_i} ,\mathop x\nolimits_{_j} } \right) + \varsigma \displaystyle\sum\limits_{i = 1}^l {\left( {\mathop \alpha \nolimits_i^* + \mathop \alpha \nolimits_i } \right) - \displaystyle\sum\limits_{i = 1}^l {\mathop y\nolimits_i \left( {\mathop \alpha \nolimits_{_i^*} - \mathop \alpha \nolimits_{_i} } \right)} } \\ {\rm {s.t.}}\begin{array}{*{20}{c}} {}&{} \end{array}\mathop {0 \le \alpha }\nolimits_i^* ,\mathop \alpha \nolimits_i \le C,\displaystyle\sum\limits_{i = 1}^l {\left( {\mathop \alpha \nolimits_{_i^*} - \mathop \alpha \nolimits_{_i} } \right) = 0} ,i = 1,2,\cdots,l \\ \end{array} \right.$ | (11) |
多核支持向量机的预测函数为:
| $f\left( x \right) = \sum\limits_{i = 0}^l {\left( {\mathop \alpha \nolimits_i^* - \mathop \alpha \nolimits_i } \right)} K\left( {\mathop x\nolimits_{_i} ,\mathop x\nolimits_{_j} } \right) + b$ | (12) |
灰狼优化算法[9](Grey Wolf Optimizer, GWO)的寻优原理取自于灰狼群体的等级机制和狩猎方式, 捕食行动由头狼领导, 其它灰狼个体进行围攻. 采用GWO求解函数优化问题时,
首先, 灰狼群体通过式(13)–式(17)对猎物进行包围.
| $D = \left| {C \cdot {X_p}(t) - X(t)} \right|$ | (13) |
| $\begin{split} \\ X(t) = {X_p}(t) - A \cdot D \end{split}$ | (14) |
| $A = 2a \cdot {r_1} - a$ | (15) |
| $C = 2 \cdot {r_2}$ | (16) |
| $a = 2 - t*\frac{2}{{{G_{\max }}}}$ | (17) |
其中,
其次, 由
| $\left\{ {\begin{split} & {D_\alpha } = \left| {{C_1} \cdot {X_\alpha }(t) - X(t)} \right|,{X_1} = {X_\alpha } - {A_1} \cdot {D_\alpha } \\ & {D_\beta } = \left| {{C_{\rm{2}}} \cdot {X_\beta }(t) - X(t)} \right|,{X_2} = {X_\beta } - {A_{\rm{2}}} \cdot {D_\beta } \\ & {D_\delta } = \left| {{C_{\rm{3}}} \cdot {X_\delta }(t) - X(t)} \right|,{X_3} = {X_\delta } - {A_{\rm{3}}} \cdot {D_\delta } \\ & X(t{\rm{ + 1}}) = \frac{{{X_1} + {X_2} + {X_3}}}{3} \\ \end{split} } \right.$ | (18) |
最后, 灰狼群体完成攻击行为来寻获猎物. 攻击行为主要通过式(15)来实现. 当
目前GWO在许多领域得到了广泛的应用, 如车辆路径问题[10]、多目标优化[11]、函数优化[12]和入侵检测[13]等. 然而, 灰狼优化算法存在求解精度不高和收敛速度较慢等不足, 对此, 研究学者多在收敛因子改进和位置更新方面进行改进[14-19].
(1)基于云模型理论改进收敛因子
灰狼优化算法存在探索能力(全局搜索)和开发能力(局部搜索)两种操作. 当系数
Step 1. 产生一个以En为期望值, He为标准差的正态随机数En';
Step 2. 取
Step 3. 利用公式
本文期望
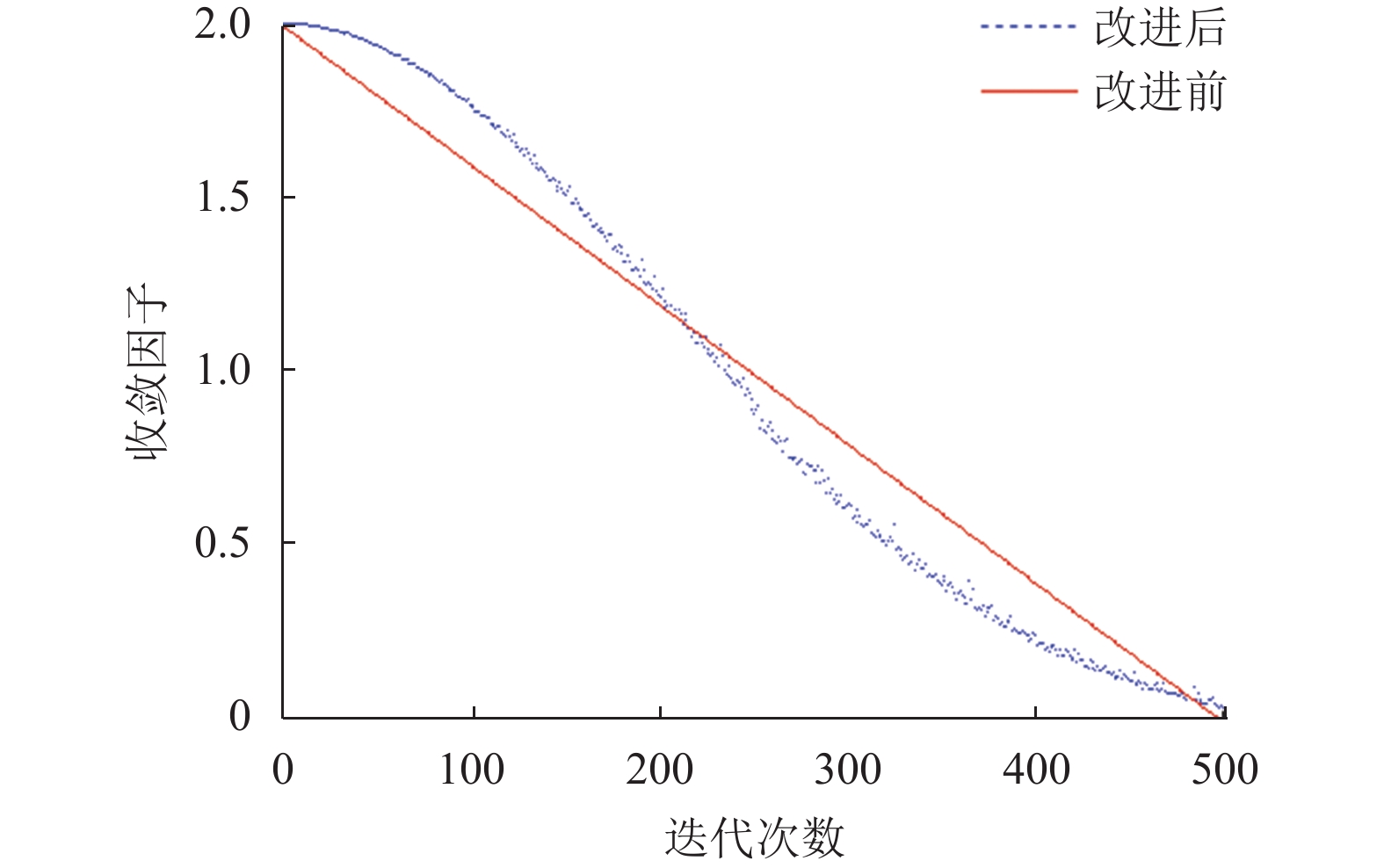
|
图 1 收敛因子变化图 |
(2)基于二次插值的头狼个体更新机制
灰狼优化算法在求解高维优化问题时, 搜索空间规模较大造成后期收敛速度慢, 寻优能力降低, 其原因算法局部探索能力较差, 如果对全局最优位置进行局部探索, 则能够提高算法的收敛速度, 依据灰狼进化原理, 当前最优解也是通过三个位置的累加和确定头狼的移动方向, 具有一定的随机性. 本文对头狼的更新机制采用二次插值算法, 提升算法的局部探索能力, 如果通过二次插值得到的新解优于当前最优解则替换, 否则不做任何操作. 当前最优解X*在二次插值中起到导向的作用, 使搜索代理在其附近精细搜索, 能强化搜索个体在当代最优解的精细搜索能力.
| $\left\{ \begin{array}{l} X_\alpha '(t) = {\rm{0}}{\rm{.5}} \times \dfrac{{\left( {X_{_\beta }^2(t) - X_{_\delta }^2(t)} \right) \times f({X_\alpha }(t)) + \left( {X_{_\delta }^2(t) - X_{_\alpha }^2(t)} \right) \times f({X_\beta }(t)) + \left( {X_{_\alpha }^2(t) - X_{_\beta }^2(t)} \right) \times f({X_\delta }(t))}}{{\left( {X_{_\beta }^{}(t) - X_{_\delta }^{}(t)} \right) \times f({X_\alpha }(t)) + \left( {X_{_\delta }^{}(t) - X_{_\alpha }^{}(t)} \right) \times f({X_\beta }(t)) + \left( {X_{_\alpha }^{}(t) - X_{_\beta }^{}(t)} \right) \times f({X_\delta }(t)) + \mu }} \\ {X_\alpha }(t) = X_\alpha '(t),\begin{array}{*{20}{c}} {}&{} \end{array}{\rm {if}}\begin{array}{*{20}{c}} {}&{} \end{array}f(X_\alpha '(t)) < f({X_\alpha }(t)) \\ \end{array} \right.$ | (19) |
同时为了避免迭代后期
(3)基于动态权重策略的个体更新
在基本灰狼算法中
| $\left\{ \begin{array}{l} W_\alpha ^1 = \dfrac{{{f_\alpha } + {f_\beta } + {f_\delta }}}{{{f_\alpha }}},W_\beta ^1 = \dfrac{{{f_\alpha } + {f_\beta } + {f_\delta }}}{{{f_\beta }}},W_\delta ^1 = \dfrac{{{f_\alpha } + {f_\beta } + {f_\delta }}}{{{f_\delta }}} \\ W_\alpha ^2 = \dfrac{{\left| {{X_1}} \right|}}{{\left| {{X_1}} \right| + \left| {{X_2}} \right| + \left| {{X_3}} \right|}},W_\beta ^2 = \dfrac{{\left| {{X_{\rm{2}}}} \right|}}{{\left| {{X_1}} \right| + \left| {{X_2}} \right| + \left| {{X_3}} \right|}},W_\delta ^2 = \dfrac{{\left| {{X_{\rm{3}}}} \right|}}{{\left| {{X_1}} \right| + \left| {{X_2}} \right| + \left| {{X_3}} \right|}} \\ {W_1} = \dfrac{{\sqrt {W_\alpha ^1*W_\alpha ^2} }}{{\sqrt {W_\alpha ^1*W_\alpha ^2} + \sqrt {W_\beta ^1*W_\beta ^2} + \sqrt {W_\delta ^1*W_\delta ^2} }} \\ {W_2} = \dfrac{{\sqrt {W_\beta ^1*W_\beta ^2} }}{{\sqrt {W_\alpha ^1*W_\alpha ^2} + \sqrt {W_\beta ^1*W_\beta ^2} + \sqrt {W_\delta ^1*W_\delta ^2} }} \\ {W_{\rm{3}}} = \dfrac{{\sqrt {W_\delta ^1*W_\delta ^2} }}{{\sqrt {W_\alpha ^1*W_\alpha ^2} + \sqrt {W_\beta ^1*W_\beta ^2} + \sqrt {W_\delta ^1*W_\delta ^2} }} \\ \end{array} \right.$ | (20) |
(4)基于混沌策略的个体随机游走
为克服种群多样性衰减太快导致趋向局部最优而早熟的问题, 可以采用混沌映射在局部收敛区域外的空间范围内进行全局搜索. 为保持优化过程中的种群的多样性, 选取适应值最差个体
| ${x'_w} = \cos (k\arccos {x_w});\;\;k = 2$ | (21) |
本文所构建的多核支持向量机采用多项式核函数和RBF核函数, 因此需要优化的参数分别为惩罚因子、RBF和多项式核函数的核参数以及权重. 采用改进灰狼算法对于上述参数进行优化, 具体流程如下.
(1) 灰狼种群个体初始化. 将优化参数组合在一起作为灰狼个体进行编码, 并设定各参数的取值范围并初始化. 设定种群规模 m, 最大迭代次数maxiter, 初始化
(2) 将支持向量回归机的期望输出
| $MSE = \frac{1}{N}\sum\limits_{i = 1}^N {{{({o_i} - {y_i})}^2}} $ | (22) |
(3) 灰狼种群的所有个体根据式(22)计算适应度, 并将适应度最好的个体作为
(4) 利用基于云模型理论算法计算收敛因子
(5) 当迭代次数达到最大迭代次数maxiter或适应度的值满足要求时停止迭代, 得到多核支持向量回归机优化参数, 建立采油速度预测模型.
4 实验仿真 4.1 改进灰狼优化算法寻优性能对比为了验证 ICGWO 算法的寻优性能, 选取单峰、多峰和固定维度多峰6 个基准测试函数进行测试, 6个优化函数如表1所示. 同时选取基本GWO算法、文献[14] IGWO算法、文献[15] AL-GWO算法、文献[16]提出的 CGWO1算法和文献[17]提出的CGWO2进行对比. 仿真实验的运行环境为 IntelCore i7 CPU, 主频2.20 GHz, 内存8 GB, Windows 10操作系统, 实验仿真软件采用Matlab R2015a. 所有对比算法种群个数统一设置为30, 最大迭代次数maxiter设置为500次, 优化维度除F5和F6之外都设置为100维. 实验独立运行10次, 对比各个算法的平均值和标准差结果如表2所示.
| 表 1 优化函数 |
| 表 2 对比结果 |
从表2的对比结果可知, 本文所提算法在对仿真函数的优化过程中都取得了最好的结果, 对于优化函数1、2和4都在迭代次数内寻找到最优解. IGWO寻优效果次之. 分析其原因本文通过云模型改进收敛因子, 基于二次插值的头狼个体更新机制和动态权重策略, 可以很好地平衡全局探索和局部寻优, 有利于加速寻优速度, 这种改进在单峰函数中效果尤为明显, 与GWO相比都找到了最优值. 上述改进结合基于混沌策略的个体随机游走对于多峰函数的寻优也明显优于GWO, 增加了跳出局部最优解的概率. 虽然IGWO、CGWO1和CGWO2都对收敛因子采用非线性方法计算, 但都属于采用一条精确曲线, 而本文利用云模型定性概念与定量描述的不确定转换来完成收敛因子的计算, 能更好地平衡全局搜索与局部搜索之间的寻优能力. IGWO和CGWO2 采用权重的方式对灰狼个体的更新方式进行改进, 通过实验结果可以得出IGWO的性能要优于CGWO2, 但次于ICGWO, 这是由于ICGWO不但考虑了位置向量对灰狼寻优位置的影响, 同时也考虑了3个最优狼本身适应度对群狼号召力的影响, CGWO1通过对随机扰动对头狼个体进行改进存在一定的随机性, 而ICGWO则通过二次插值的方式通过当前3个较优解来加速局部寻优, 具有一定的确定性, 因此, 通过以上改进原理的对比和实验结果可知, 本文算法都优于其他对比算法, 具有很好的搜索能力和良好的稳定性, 且收敛精度较高.
4.2 基于多核支持向量回归机的采油速度预测(1)实际数据预处理
针对实际地质数据和开发数据, 应用灰色关联分析理论的对采油速度影响因素的重要性进行分析. 以采油速度为参考序列, 含水率、地层压力、流压、有效厚度、地质储量、渗透率、束缚水饱和度、含水上升速度和压力恢复速度等多个影响因素为比较序列, 利用均值法无量纲化, 取分辨系数为0.5, 得到不同分类油层的采油速度影响因素的关联度大小排序. 最后选取含水、地层压力、流压、有效厚度、渗透率、束缚水饱和度6个属性用于确定采油速度.
(2)实例验证
首先选取油田某区块2019年168口油井每月的含水率、地层压力、流压、有效厚度、渗透率、束缚水饱和度和采油速度共2016条数据进行实例验证, 选用2019年1月到9月的数据作为训练数据集, 2019年10月到12月的数据作为测试数据集. 分别采用静态影响因素分析法、动态影响因素分析法、多项式支持向量回归机(PLOY-SVR)、RBF支持向量回归机(RBF-SVR)、基于GWO优化的多核支持向量机(GWO-MCSVR)和基于ICGWO优化的多核支持向量回归机(GWO-MCSVR)进行对比. 采用均方误差(Mean Squared Error, MSE)和平均绝对误差(Mean Absolute Error, MAE)来对比各种算法的预测效果. 1月到9月的训练数据集对比数据如表3所示, 10月到12月的测试集对比结果如表4所示.
| 表 3 训练样本对比结果 |
| 表 4 测试样本结果 |
采油速度静态影响因素分析法计算方法如式(23):
| ${V_0} = {\rm {lg}}[{(K{\rm{*}}h/\mu )^a}] + b*{\eta ^c} - d$ | (23) |
其中,
动态影响因素分析法计算方法如式(24):
| ${V_o} = \frac{1}{{b\left( {1 - {S_{wc}}} \right)}} \cdot \frac{1}{{{f_w}\left( {1 - {f_w}} \right)}} \cdot f_w'$ | (24) |
其中,
从表3可知, ICGWO优化的多核支持向量机的拟合效果最好, 多核支持向量回归机的拟合效果要优于单核回归机, 静态影响因素分析法、动态影响因素分析法的拟合结果较差. 主要原因是这两种方法都是基于经验公式拟合, 且考虑影响因素较少, 拟合结果受数据的分布情况影响较大. 多个核函数的优化组合可以弥补单一核函数选择盲目性的不足, 可以充分地提取数据的隐含信息. 从表4可知ICGWO-MCSVR对10月到12月的采油速度预测效果最好, 这是因为模型充分利用多核学习的优势, 以及利用ICGWO算法较好的寻优性能完成对核函数参数、惩罚因子和权值系数的最优选择.
5 结论利用多核学习支持向量回归机模型预测采油速度, 针对模型中权值系数, 惩罚因子核和核参数的选择问题, 提出一种改进的灰狼优化算法, 算法利用云模型改进收敛因子的计算方式, 较好的平衡了算法全局和局部寻优性能, 利用二次插值方式改进了头狼的进化方式加速局部寻优. 实验结果表明, 经过优化的模型参数构造的多核支持向量回归机, 其预测精度相比较单核支持向量机来说有明显得提高.
| [1] |
赵伦, 陈希, 陈礼, 等. 采油速度对不同黏度均质油藏水驱特征的影响. 石油勘探与开发, 2015, 42(3): 352-357. |
| [2] |
吴文有, 王禄春, 张继风, 等. 特高含水期油田采油速度主要影响因素. 大庆石油地质与开发, 2012, 31(5): 51-55. DOI:10.3969/J.ISSN.1000-3754.2012.05.010 |
| [3] |
姜凤光, 王小林. 采油速度影响因素及理论值研究. 西南石油大学学报(自然科学版), 2013, 35(6): 104-108. |
| [4] |
陈军, 杨峻懿, 刘启国. 特高含水期油藏采油速度研究及影响因素分析. 油气藏评价与开发, 2018, 8(4): 17-21, 32. DOI:10.3969/j.issn.2095-1426.2018.04.004 |
| [5] |
吕达, 刘文婧, 陈肖洁. 规则的多核学习支持向量回归算法. 机械设计与制造, 2016(12): 53-56. DOI:10.3969/j.issn.1001-3997.2016.12.014 |
| [6] |
邵朝, 李强. 基于特征加权的多核支持向量机. 西安邮电大学学报, 2017, 22(2): 84-88. |
| [7] |
Li Y, Zhu ZC, Hou AL, et al. Pulmonary nodule recognition based on multiple kernel learning support vector machine-PSO. Computational and Mathematical Methods in Medicine, 2018, 2018: 1461470. |
| [8] |
杜伟, 房立清, 齐子元, 等. 基于LFOA优化多核支持向量机的液压泵故障诊断. 机械设计与研究, 2018, 34(1): 137-140, 144. |
| [9] |
Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61. |
| [10] |
黄戈文, 蔡延光, 戚远航, 等. 自适应遗传灰狼优化算法求解带容量约束的车辆路径问题. 电子学报, 2019, 47(12): 2602-2610. |
| [11] |
鲍毅, 戴波, 汪志华, 等. 基于灰狼算法的多目标智能家居负荷控制算法. 系统仿真学报, 2019, 31(6): 1216-1222. |
| [12] |
张新明, 王霞, 康强. 改进的灰狼优化算法及其高维函数和FCM优化. 控制与决策, 2019, 34(10): 2073-2084. |
| [13] |
徐慧, 付迎春, 刘翔, 等. 融合杜鹃搜索的灰狼优化算法在网络入侵检测特征选择中的应用. 工程科学与技术, 2018, 50(5): 160-166. |
| [14] |
郭振洲, 刘然, 拱长青, 等. 基于灰狼算法的改进研究. 计算机应用研究, 2017, 34(12): 3603-3606, 3610. DOI:10.3969/j.issn.1001-3695.2017.12.019 |
| [15] |
郭阳, 张涛, 胡玉蝶, 等. 基于自适应头狼的灰狼优化算法. 成都大学学报(自然科学版), 2020, 39(1): 60-63, 73. |
| [16] |
谈发明, 赵俊杰, 王琪. 一种改进非线性收敛方式的灰狼优化算法研究. 微电子学与计算机, 2019, 36(5): 89-95. |
| [17] |
晏福, 徐建中, 李奉书. 混沌灰狼优化算法训练多层感知器. 电子与信息学报, 2019, 41(4): 872-879. DOI:10.11999/JEIT180519 |
| [18] |
Luo KP, Zhao QH. A binary grey wolf optimizer for the multidimensional knapsack problem. Applied Soft Computing, 2019, 83: 105645. DOI:10.1016/j.asoc.2019.105645 |
| [19] |
Gupta S, Deep K. A novel random walk grey wolf optimizer. Swarm and Evolutionary Computation, 2019, 44: 101-112. |
 2021, Vol. 30
2021, Vol. 30


