1 引言

磁共振成像(Magnetic Resonance Imaging, MRI)是以核磁共振(Nuclear Magnetic Resonance, NMR)为物理基础的一种成像技术, 该技术通过在静磁场中将一定频率的射频脉冲施加到人体上, 以刺激人体内的氢质子引起共振现象. 与计算机X射线断层扫描成像技术(Computed Tomography, CT)相比, MRI不仅无需使用造影剂和没有电离辐射, 而且可以直接做出横断面、矢状面和冠状面等优点^[1]. 压缩感知^[2]理论的提出, 打破了传统的奈奎斯特采样定律的限制. 基于压缩感知的磁共振成像(CS-MRI)^[3]技术大大推动了磁共振成像的发展. 基于CS-MRI的重构问题可以表示如下:

$\mathop {\min }\limits_X \frac{1}{2}\left\| {Y - UFX} \right\|_F^2 + \lambda {\left\| {\Psi X} \right\|_1}$

(1)

其中, $X \in {\mathbb{C}^{\sqrt N \times \sqrt N }}$ 为重构的磁共振图像; $F \in {\mathbb{C}^{\sqrt N \times \sqrt N }}$ 为离散傅里叶变换; $U \in {\mathbb{R}^{\sqrt M \times \sqrt N }}$ (M<N)为欠采样矩阵; $Y \in {\mathbb{C}^{\sqrt M \times \sqrt N }}$ 是欠采样的K空间数据, $\Psi $ 代表着稀疏变换(例如离散余弦变换, 全变差变换, 小波变换等); 参数 $\lambda $ 是用来平衡数据保真项和稀疏项的惩罚参数.

图像去噪是一个较为成熟的研究领域, 实现去噪的途径之一是利用图像的稀疏性. 常用的图像稀疏方法有傅里叶变换、全变差变换、小波变换以及字典学习等. 近年来, 基于非局部自相似块思想^[4]的低秩去噪方法在CS-MRI领域中得到应用. 非局部自相似性的原理通过在图像中寻找与参考块相似的相似块组, 利用该相似块组所组成的矩阵具有的低秩属性进行图像去噪. 求解矩阵的秩函数是NP难问题, 常使用核范数来近似代替秩函数的求解. 其中最经典的方法是核范数最小化^[5]算法. NNM通过对待修复的矩阵奇异值分解, 对奇异值进行阈值处理来求解核范数最小化问题, 该方法称为奇异值阈值算法(Singular Value Thresholding, SVT). 由于NNM平等的对每个奇异值进行收缩, 忽略了矩阵奇异值的差异. 在此基础上, Dong提出了加权核范数最小化(Weighted Nuclear Norm Minimization, WNNM)^[6]算法, 针对不同大小的奇异值, 设定不同的权值进行收缩, 得到了更好的秩最小化问题的解, 实验表明较NNM其保留更多原始图像的边缘信息, 去噪性能更高. 研究表明, Schatten-p范数是一种比核范数更加逼近低秩矩阵的范数, Xie等^[7]在2016年提出加权Schatten-p范数最小化(Weighted Schatten p-norm Minimization, WSNM)去噪问题, 该方法比WNNM具有更好的去噪性能.

CS-MRI重建算法的研究一直是MRI领域研究的热门之一. 迭代阈值算法(Iterative Shrinkage Thresholding Algorithm, ISTA)^[8]是一种实现简单、计算量小并且性能较为稳定的算法. Zhang等^[9]利用小波变换实现图像的稀疏化结合ISTA算法最终实现了CS-MRI重构. 由于ISTA算法具有收敛速度慢的缺点, Beck等^[10]提出了快速迭代软阈值算法(Fast Iterative Shrinkage Thresholding Algorithm, FISTA), 从探究多步级的方法来加速算法收敛速度或者从优化小波子带宽参数两个方向来实现优化重构问题. 在ISTA和FISTA算法的基础上, Huang等^[11]提出了快速混合分裂算法(Fast Composite Splitting Algorithm, FCSA). FCSA算法结合了变量分裂和运算分裂两种算法, 将原问题分解为最小化全局差分约束问题和最小化 ${L_1}$ 范数约束的两个子问题. 通过线性结合两个子问题的解并加入加速步骤得到最终解. 除此以外, 交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)^[12]算法是以增广拉格朗日算法为基础的一种常用的图像重构算法. ADMM在迭代过程中将目标函数进行变量分离, 通过分而治之的思想将原问题分解为多个交替的子问题, 使得原问题的求解转换成较为简单的子问题求解. 近似消息传递算法(Approximate Message Passing, AMP)^[13]是在消息传递算法的基础上, 用来求解图像的结构化稀疏约束的重构模型. 针对图像重构领域, AMP通过结合图像的结构先验信息, 在其迭代过程中滤出噪声, 迭代逼近原始图像^[14]. 文献[15]构建了基于去噪的近似消息传递算法(Denoising-based Approximate Message Passing, DAMP), 利用经典的降噪模型作为算法的先验知识实现DAMP迭代过程中的滤波操作, 最终重构出图像.

本文提出了一种基于自适应低秩去噪的近似消息传递的磁共振图像重构算法. 我们使用去噪的近似消息传递重构算法, 在重构过程中使用自适应的加权Schatten-p范数最小化去噪方法, 根据估计的噪声标准差来设定WSNM的图像块大小和相似块的数量. 使用真实的全采样磁共振图像作为实验对象, 实验表明本文提出的方法具有较高的重建性能并且能够保留更多的图像信息.

2 基于自适应低秩去噪的磁共振图像重构算法 2.1 自适应Schatten-p范数最小化

矩阵的核范数定义如下:

${\left\| X \right\|_*} = \sum\limits_{{i} = 1}^{\min \left( {m,n} \right)} {\left| {{\sigma _{i}}\left( X \right)} \right|} $

(2)

矩阵的核范数等于矩阵进行SVT分解后矩阵奇异值的绝对值之和. 核范数最小化(NNM)问题可以表示成如下所示:

$\mathop X\limits^ \wedge = \arg \mathop {\min }\limits_X \left\| {M - X} \right\|_F^2 + \lambda {\left\| X \right\|_*}$

(3)

以X的核范数作为约束条件, 其中M是含有噪声的观测矩阵, 核范数最小化问题就是从已知的M中恢复矩阵X. 其中 $\lambda $ 为正参数. $\mathop X\limits^ \wedge $ 的求解过程如算法1所示.

算法1. 核范数最小化求解(NNM)

输入: 观测矩阵M和阈值 $\scriptstyle \lambda$ .

输出: $\scriptstyle \mathop X\limits^ \wedge$ .

$\scriptstyle M = U\sum {{V^{\rm T}}}$ ; //对M使用SVT分解;

$\scriptstyle {S_\lambda }{\left( {\sum\limits_i {} } \right)_{ii}} = \max \left( {\sum\limits_{ii} { - \lambda } ,0} \right)$ ;

$\scriptstyle \mathop X\limits^ \wedge {\rm{ = }}U{S_\lambda }\left( {\sum {} } \right){V^{\rm T}}$ ;

NNM通过对奇异值进行软阈值操作, 进而保留了图像的低秩结构特性和信息. 由于, NNM中软阈值操作设定每个奇异值的权重均相同, 这种设置忽略了奇异值自身带来的物理意义, 并不是低秩求解问题的最优解. 在此基础上提出加权核范数最小化(WNNM)方法. 该方法给予大奇异值大的权值、小奇异值小权值, 充分考虑了奇异值的物理意义, 使得图像中更多有用的信息被保留下来. 其加权核范数定义为:

${\left\| X \right\|_{w,*}} =\displaystyle \sum\limits_i^{\min \{ n,m\} } {{{\left| {{w_i}{\sigma _i}(X)} \right|}_1}} $

(4)

其中, ${w_i}$ 表示奇异值权重. 当 ${w_i}{\rm{ = 1}}$ 时, WNNM问题变成了NNM问题. 因此, NNM是WNNM的一个特殊情况. 基于WNNM的图像去噪模型如下所示:

$\mathop {{X_j}}\limits^ \wedge = \mathop {\arg \min }\limits_{{X_j}} \dfrac{1}{{\beta _n^2}}\left\| {{M_j} - {X_j}} \right\|_F^2 + {\left\| {{X_j}} \right\|_{w,*}}$

(5)

给定含噪图像M, 利用图像的非局部自相似性找到对应的相似块组 ${M_j}$ , 利用式(5)估计对应的原始清晰图像块 ${X_j}$ ; 其中 $\beta _n^2$ 是图像的噪声方差. 待求得整幅图像的相似块组后, 对图像块组进行聚合就能够求得去噪后的清晰图像.

除核范数以外, Schatten-p范数是秩函数的一种非凸近似函数. 文献[16,17]提出了使用Schatten-p范数来实施低秩正则化的方法, 定义矩阵奇异值的 ${L_p}$ 范数为Schatten-p范数, 其中 ${{0 < p}} \le {\rm{1}}$ . 从理论上讲, Schatten-p范数能够更准确地恢复信号. 在WNNM的基础上, 提出了加权Schatten-p范数最小化(WSNM).

矩阵 $X \in {\mathbb{R}^{n \times m}}$ 的加权Schatten-p范数定义如下:

${\left\| X \right\|_{w,s}} = \left({\sum\nolimits_i^{\min \{ n,m\} } {w_i}{\sigma _i}{{(X)}^p}}\right)^{{\frac{1}{p}}} ,0 < p \le 1$

(6)

其中, $w = [{w_1},{w_2},\cdots,{w_{\min \{ n,m\} }}]$ 表示权重向量, 式(6)的p次方为:

$\left\| X \right\|_{w,s}^p = \sum\nolimits_i^{\min \{ n,m\} } {{w_i}{\sigma _i}{{(X)}^p}} ,0 < p \le 1$

(7)

则利用加权Schatten-p范数最小化进行图像去噪描述成如下数学模型:

$\mathop {{X_j}}\limits^ \wedge = \arg \mathop {\min }\limits_X \frac{1}{{\beta _n^2}}\left\| {{M_j} - {X_j}} \right\|_F^2 + \lambda \left\| {{X_j}} \right\|_{w,s}^p$

(8)

权重向量 ${w_k}$ 是WSNM去噪的关键步骤之一, 求解如下:

${w_k} = \frac{{c\sqrt n }}{{\left( {\delta _k^{1/p}\left( {\mathop {{X_j}}\limits^ \wedge } \right) + \varepsilon } \right)}}$

(9)

其中, n表示图像的相似块数量, $\varepsilon $ 是一个非常小的正数, 用来防止除数为0, $c = 2\sqrt 2 \beta _n^2$ , ${\delta _k}$ 表示矩阵 ${\mathop {X_j}\limits^ \wedge}$ 的第k奇异值. 文献[7]证明WSNM可以等价地转化为独立的非凸权重 ${L_p}$ 范数子问题:

$\mathop {\min }\limits_{{\sigma _1}, \cdots ,{\sigma _{\min \{ m.n\} }}} \displaystyle\sum\limits_{i = 1}^{\min \{ m,n\} } {\left( {\dfrac{1}{2}{{({\delta _i} - {\sigma _i})}^2} + \lambda {w_i}\sigma _i^p} \right)} $

(10)

其中, ${\delta _i}$ 为观测矩阵M的第i个奇异值. 式(10)的求解可以通过广义软阈值(Generalized Soft-Thresholding, GST)^[18]算法获得全局最优解, 最终求得 $\mathop X\limits^ \wedge $ :

$\mathop X\limits^ \wedge = {U_M} \times S_p^{GST}\left({\sum _M};\lambda w\right) \times V_M^{\rm T}$

(11)

其中, $M = {U_M}{\Sigma _M}V_M^{\rm T}$ , ${\Sigma _M}$ 是奇异值对角矩阵.

本文使用WSNM去噪时, 根据当前的噪声标准差大小自适应地设置WSNM的图像块大小以及相似块的个数, 该设置对磁共振图像重构结果具有微弱的影响, 不同噪声标准差下WSNM去噪的图像块大小以及相似块个数设置如表1所示.

2.2 基于自适应WSNM的磁共振图像重构算法

近似消息传递算法是基于迭代软阈值的信号重建技术. AMP迭代过程中, 残差的更新使用了Onsager校正项来求解, Onsager校正项使用蒙特卡洛方法近似求解. 而去噪近似消息传递算法(DAMP)是基于噪声去除的AMP算法, 以图像去噪来实现AMP的滤波操作. 本文将改进的自适应WSNM方法作为AMP迭代滤波的去噪函数以实现图像压缩感知重构. 用 ${D_{{\sigma ^t}}}$ 表示整个去噪算法, 借助独立同分布向量来估计去噪函数的散度. MRI的观察模型如下:

$y = {F_u}\tilde x + \eta $

(12)

其中, $\tilde x$ 是向量形式的重构图像; ${F_u}$ 表示欠采样傅里叶操作算子; y是观测数据, N表示观测数据y的长度大小; $\eta $ 是观察噪声.

基于CS-MRI的DAMP模型如下:

${r_k} = {x_{k - 1}} + F_u^{\rm T}{{\textit{z}}_{k - 1}}$

(13)

${\sigma _{k}} = \frac{{{{\left\| {{{\textit{z}}_{k - 1}}} \right\|}_2}}}{{\sqrt N }}$

(14)

${x_{k}} = {D_{{\sigma _k}}}\left( {{r_k}} \right)$

(15)

${o_{k}} = {{\textit{z}}_{k - 1}}D'_{{\sigma _k}}\left( {{r_k}} \right)/M$

(16)

${{\textit{z}}_{k}} = y - {F_u}{x_k} + {o_k}$

(17)

其中, $F_u^{\rm T}$ 是 ${F_u}$ 的伴随运算符, $F_u^{\rm T}y$ 表示零填充的重构图像. ${r_k}$ 是压缩感知逆投影后的含噪图像. ${D_{{\sigma _k}}}$ 和 ${\sigma _k}$ 分别表示第k次图像去噪和噪声标准差. ${x_k}$ 和 ${{\textit{z}}_k}$ 分别表示第k次迭代图像x的估计值和迭代残差. ${o_k}$ 是Onsager校正项, 其中 $D'_{{\sigma _k}}$ 表示该去噪算法的散度, 使用蒙特卡洛法来近似求解, 如下所示:

$D'_\sigma \approx \frac{1}{\tau }{b^H}\left( {{D_\sigma }\left( {x + \tau b} \right) - {D_\sigma }\left( x \right)} \right)$

(18)

其中, $b$ 是满足 $b \sim N\left( {0,I} \right)$ 的随机向量, $\tau $ 是一个数值很小的常数, 文献[15]证明了Onsager校正项的存在能够保证DAMP算法的快速收敛. 在本章中, 我们使用WSNM算法实现迭代过程中的图像去噪处理 ${D_\sigma }$ , 我们称此算法为基于自适应WSNM去噪的DAMP磁共振图像重构算法(简称WSNM-AMP-MRI). 算法2展示了基于自适应WSNM的近似消息传递算法.

算法2. WSNM-AMP-MRI重构算法

输入: 观测数据 $\scriptstyle y$ ; 欠采样操作算子 $\scriptstyle {F_u}$ ; 初始 $\scriptstyle {x_{\rm{0}}}{\rm{ = }}F_u^{\rm T}{y}$ ;

输出: 重构磁共振图像 $\scriptstyle x$ .

for $\scriptstyle k \le K$ then

　　 $\scriptstyle {r_k} = {x_{k - 1}} + F_u^{\rm T}{{\textit{z}}_{k - 1}}$

　　 $\scriptstyle {\sigma _k} = \frac{{{{\left\| {{{\textit{z}}_{{{k - 1}}}}} \right\|}_2}}}{{\sqrt N }}$

　　 $\scriptstyle {x_k} = {D_{{\sigma _k}}}{\left( {{r_k}} \right)_{\rm WSNM}}$

　　 $\scriptstyle {o_{k}} = {{\textit{z}}_{k - 1}}D'_{{\sigma _k}}{\left( {{r_k}} \right)_{\rm WSNM}}/M$

　　 $\scriptstyle {{\textit{z}}_{k}} = y - {F_u}{x_k} + {o_k}$

　　 $\scriptstyle k = k + 1$

end

3 实验结果及分析

为了验证本章提出的WSNM-AMP-MRI的重构性能, 我们选用两张MR图像进行模拟实验, 它们分别是心脏(Heart)和大脑(Brain)磁共振图像, 其中大脑数据来源于文献[19], 心脏数据来源于文献[20]. 使用了笛卡尔采样和伪径向采样两种模式对原始图像欠采样. 图1分别展示了使用的实验磁共振图像以及采样mask (采样率为25%的条件下).

对比实验有平移不变离散小波变换(Shift-Invariant Discrete Wavelet, SIDWT)^[21], 基于方向性小波变换(Patch-based Directional Wavelets, PBDW)^[22]和基于自相似性的非局部算子(Patch-based Nonlocal Operator, PANO)^[23]的磁共振图像重构算法, 与WSNM-AMP-MRI方法进行比较. 对比实验中, SIDWT、PBDW和PANO重构方法将设置最优参数使得重构结果最佳. 实验中, WSNM-AMP-MRI重建算法的参数设置如下: 正则化参数 $\lambda $ =1e–6, p=0.7. 同时, 使用峰值信噪比(Peak Signal to Noise Ratio, PSNR)和相对 ${L_2}$ 范数误差(Relative ${L_2}$ Norm Error, RLNE)作为客观评价指标衡量不同算法的重构效果. 两种客观评价指标的定义请参考式(19)和式(20). 每种方法的计算结果是通过重复10次相同的重建过程后计算结果的平均值.

${{PSNR}} = 10 \times {\log _{10}}\left(\dfrac{{{{255}^2}}}{{M \times N \displaystyle \sum\nolimits_{i = 1}^M {\displaystyle \sum\nolimits_{j = 1}^N {{{(y(i,j) - x(i,j))}^2}} } }}\right)$

(19)

$RLNE = \frac{{{{\left\| {y(i,j) - x(i,j)} \right\|}_2}}}{{{{\left\| {x(i,j)} \right\|}_2}}}$

(20)

其中, x是原始清晰图像, y是重构图像, 图像的大小是 $M \times N$ , ${\mu _x}$ 和 ${\mu _y}$ 表示x和y的均值; ${\sigma _x}$ 和 ${\sigma _y}$ 分别是x和y的方差, ${\sigma _{xy}}$ 是x和y的协方差; ${C_1}$ 和 ${C_{\rm{2}}}$ 是常数, 作用是保持稳定性.

3.1 实验结果

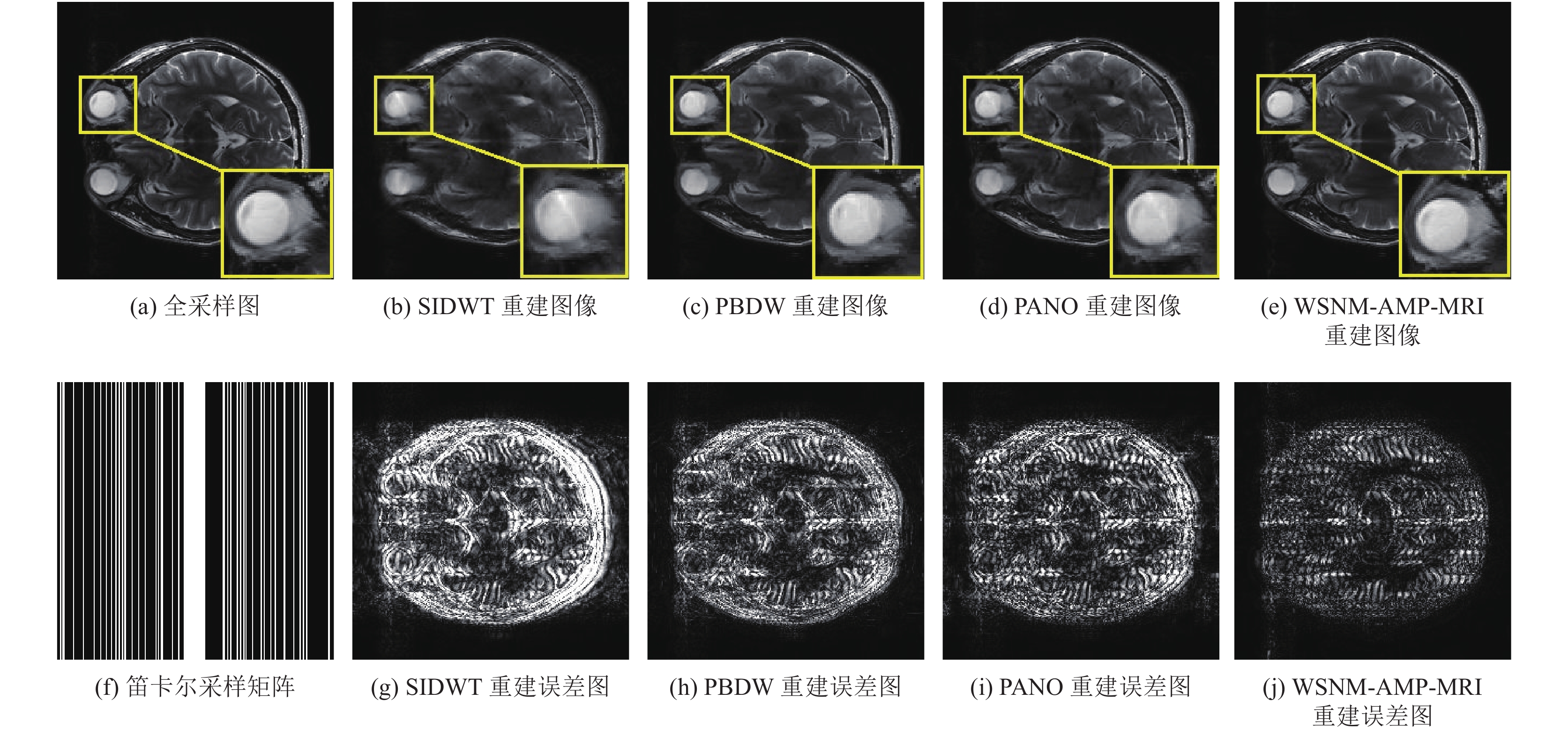
图2和图3分别展示了在不同的采样因子和采样模式下, 相应算法重构出的磁共振图像的细节放大图以及误差图. 图2展示了采样因子为4时的伪径向采样下的心脏重构结果展示图. 从细节放大图可以看到, 本章提出的WSNM-AMP-MRI算法能够保留更多的局部细节信息. 从放大了10倍的重构误差图可以看出, 本章提出的算法重构误差明显小于对比的3种重构算法的误差. 图3展示采样因子为4的笛卡尔采样下的大脑(Brain)重构结果, 可以看出笛卡尔采样重构结果产生了平移伪影, 而为径向采样重构图像不存在这个问题.

表2和表3记录了在欠采样因子为4和6的两种情况下, 不同算法重构算法的重构PSNR和RLNE值. 从表中数据可以看出, 随着采样因子的增加, 重构的PSNR和RLNE分别在降低和增加, 说明图像重构的质量在降低. 越高的采样因子重构出的图像质量相对越差. 同时可以看出, 伪径向采样下图像的PSNR和RLNE值优于笛卡尔采样下相应的重构指标. 总之, 在笛卡尔和伪径向两种采样模式下. 本文提出的WSNM-AMP-MRI可获得更高的PSNR值和更小的RLNE值, 表明了本文提出的方法能够得到更好的重建效果, 证明了算法的有效性.

3.2 不同加速因子下图像重构性能比较

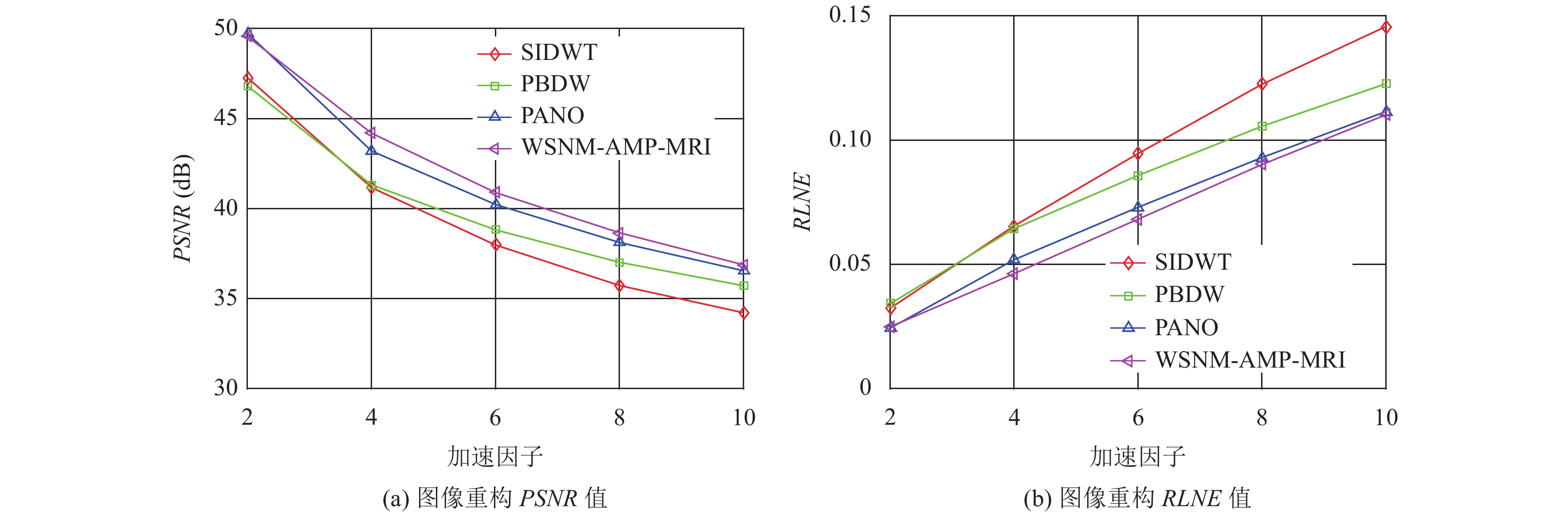
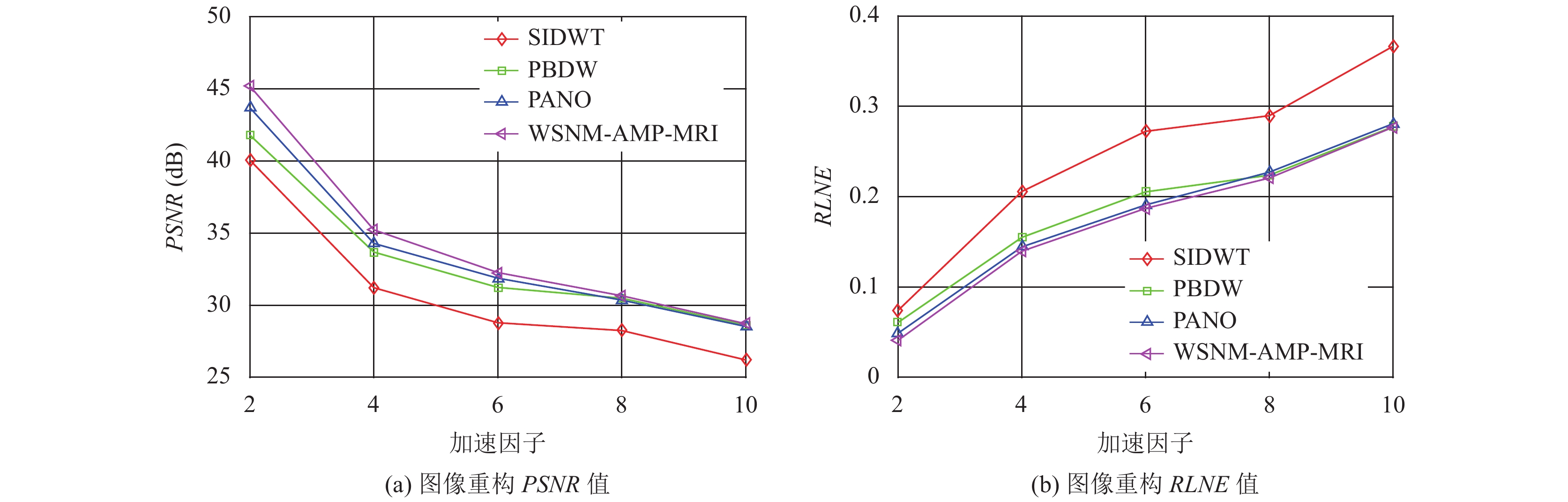
为研究不同采样率对重构结果的影响, 本实验研究了在加速因子为2、4、6、8、10时使用伪径向采样和笛卡尔采样模式下的重构结果. 本次实验选用心脏(heart)磁共振图像作为实验对象. 图4和图5展示了不同加速因子下图像重构的PSNR和RLNE走向图. 从图中可以看出 当加速因子增加时, 重构的PSNR值在减小, RLNE值在增大, 说明图像的重构质量在降低. 即采样因子越高, 图像的重构效果越差. 但是在相同采样因子的条件下, 本文所提算法的PSNR值始终高于对比实验的PSNR值, 同时RLNE值低于对比实验的RLNE值, 说明本方法在不同的采样模式以及加速因子下, 其重构质量均高于相同条件下对比实验的重构质量. 同时可以发现, 相同采样率下, 笛卡尔采样的重构质量要低于伪径向采样模式下的图像重建质量.

3.3 Schatten-p范数取值对算法重构的影响

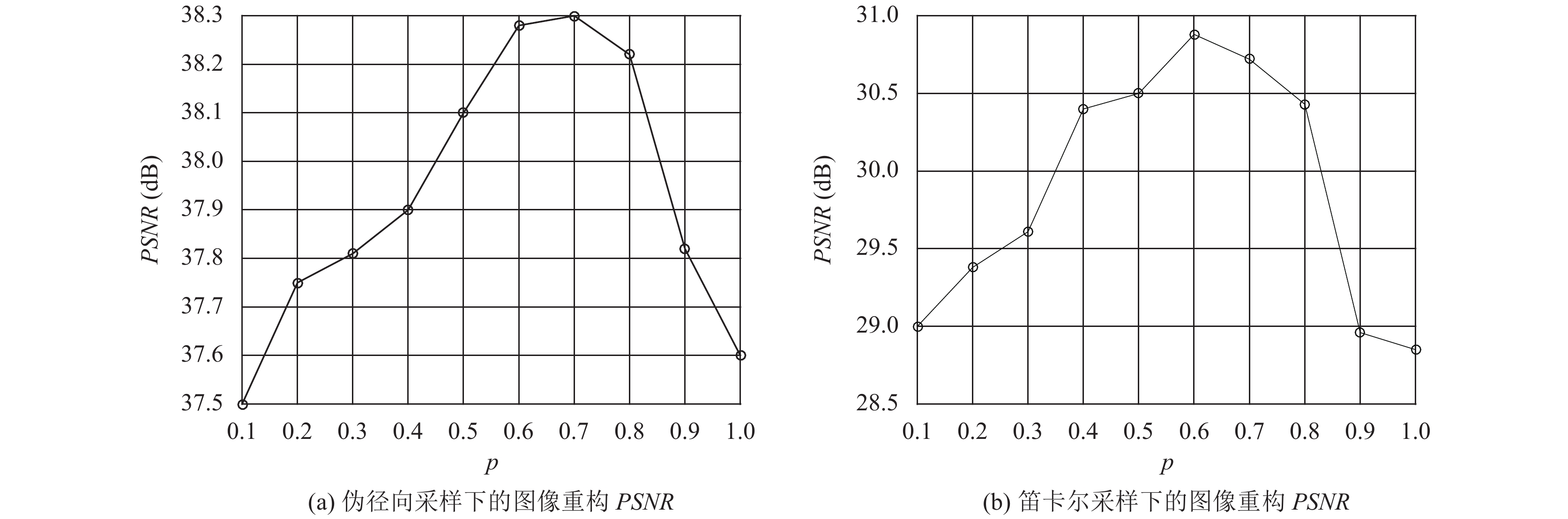
本节研究p范数的取值对磁共振图像重构的影响大小. 图6展示了在伪径向和笛卡尔采样两种模式下, p范数取不同值时, 脑部图像重构的PSNR值. 从图中可以看出, 两种采样模式下, p的取值对图像重构的影响并不相同. 整体上看, p范数的取值对两种采样模式下图像的重构质量影响并不是非常大的. 相比较笛卡尔采样模式下的重构质量而言, p范数对伪径向采样下图像的重构质量影响更大. 我们知道当p=1时, WSNM就转化为WNNM问题. 从图中可以看出, 基于Schatten-p范数的加权范数最小化去噪的图像重构PSNR值高于WNNM, 说明WSNM是一种更加优秀的逼近低秩矩阵的方法. 实验中, 当p的取值范围在[0.5, 0.7]时能够取得相对较好的重构性能.

3.4 噪声大小对重构结果的影响

本小节通过比较几种算法在含有噪声的测量数据下的重构性能, 来验证本章提出的算法的鲁棒性. 表4和表5给出在采样率为25%的条件下, 测量噪声分别为10 dB和20 dB时磁共振图像重构的PSNR值和RLNE值. 从表4中可以看出, 在测量噪声为10 dB时, 本章提出的算法具有更高的PSNR和更低的RLNE值. 同理, 表5说明在噪声为20 dB条件下本章算法仍然具有更高的重构质量. 通过将表4、表5与表2中的重构质量指标值对比, 有测量噪声的干扰条件下图像重构质量与没有测量噪声时的重构质量相比普遍降低; 并且随着噪声的增加, 磁共振图像重构的质量在降低. 因此可以得出结论, 无论在有测量噪声还是没有测量噪声的条件下, 本章提出的方法均优于对比的3种图像重构算法.

4 结论与展望

本文提出了一种基于自适应低秩去噪的近似消息传递磁共振图像重构算法. 将加权Schatten-p范数最小化作为图像的低秩约束, 再结合DAMP的特性, 根据每次迭代过程中的噪声标准差设定自适应的图像块大小以及相似块的个数, 最终重构出质量相对较好的磁共振图像. 实验结果表明, 与近几年提出的几种重建算法比较, 本文的方法可以获得更高的峰值信噪比和相对 ${L_2}$ 范数误差. 与此同时, 在测量数据加噪声的条件下观察算法的重构性能, 验证了该算法具有鲁棒性.

在本文的研究中, 参数调优是手动进行的, 在未来的工作中设计一个能够自适应调整参数的算法显得迫在眉睫. 同时, 本文提出的方法是针对二维磁共振图像的重建, 而实际生活中也会采集动态磁共振成像进行病灶诊断. 在考虑到算法重构时间和性能的基础上, 如何将本文提出的二维重建方法使用到三维动态磁共振成像是接下来的研究目标之一.