2. 轨道交通运维技术与装备四川省重点实验室, 成都 610031
2. Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Chengdu 610031, China
尿素造粒塔是尿素生产中的重要设备, 也是尿素生产流程中最后一个生产环节[1]. 其造粒原理是将成批次放置的满足加工温度要求的熔融尿素使用泵通过管道打到塔顶后喷出, 从而形成高温射流. 高温射流在下坠过程中通过空气冷却等过程快速断裂成滴, 自动凝成固体小颗粒, 从而形成颗粒状的尿素产品. 而不同批次的熔融尿素在等待被注入泵内的过程中, 其温度会随着等待时间的增加而降低. 当其开始加工时因为在等待过程中的温度变化其温度可能不符合加工温度要求. 也就是说热加工环境中工件的温度会随着其开工时刻的增大而降低, 当温度降到一定数值以后, 将不再满足加工要求, 即工时恶化问题. 此时需要对不满足加工温度要求批次的熔融尿素进行二次加热, 或者监控其温度, 当发现其温度不满足加工温度要求时立即使用保温设施对其进行保温操作. 二次加热会增加此批次熔融尿素的加工时间和消耗额外的能量, 从而增大产品拖期和能耗, 造成产品延期交货和增大生产成本; 而使用保温设施保温虽然不会增加其加工时间但是会耗费更多的能耗成本. 当造粒塔从一台扩展到多台, 此时问题便扩展为考虑不同工作模式与工时恶化的并行机调度问题. 及时交货和能耗控制是生产成本控制的重要组成部分, 因此, 如何有效保证产品及时交货以及精准的控制能耗是管理人员需要解决的关键决策问题[2]. 在此, 本文以多台尿素造粒塔的尿素生产过程为背景, 从并行机加工环境出发, 对上述调度问题进行建模并设计优化算法进行求解.
并行机调度问题长期以来吸引了大量学者的关注和研究[3], 且节能调度方面的研究已有不少. 孟磊磊等以能耗最小化为目标, 提出了5个考虑关机/重启策略的不相关并行机调度模型[4]. 周炳海与顾佳颖提出了多目标免疫克隆选择算法处理多资源约束下的非等效并行机节能调度问题[5]. 雷德明等提出了新型帝国竞争算法去处理多目标低碳并行机调度[6]. 与本文研究最为相关的则是在并行机调度问题中同时考虑节能与拖期最小化. Li等基于分派规则提出了10个启发式算法去优化能耗与总拖期[7]. 王永琦等结合问题的性质, 设计了适用于该问题的混合教学算法[8]. 然而上述研究均未考虑工件开工时间延误造成额外能耗或二次加热带来的工时恶化. 本文针对尿素厂造粒塔生产过程, 采用阶梯恶化函数对其生产过程进行描述[9], 并尽量减少生产过程中发生的能耗.
关于工时恶化的并行机调度问题亦开始受到关注, Ji和Cheng考虑了工时线性恶化情况下的并行机调度问题, 并给出了机器数确定的情况下多项式近似算法[10]. Wang等在此基础上进行了扩展, 考虑机器在开始部分不可用的情况, 并设计了启发式规则[11]. Guo等为工时阶梯恶化的并行机设计了布谷鸟搜索算法, 在考虑工件间调整时间的基础上上最小化了总拖期[12], 此外Guo等还比较了不同的建模方式对问题求解效率的影响[13]. 变邻域搜索[14]与集划分建模策略[15]也相继被用于工时阶梯恶化的并行机调度问题. 在考虑处理成本和收益的阶梯恶化并行机调度问题中, Pei等提出了变邻域搜索的混合算法去最大化净收益[16]. 遗传算法也被改进用于求解不相关并行机带恶化工件的调度问题[17]. 关于工时恶化的并行机调度问题在潜在机器扰动、学习效益与维护活动等方面均有扩展[18-20], 但文献[18-21]尚未涉及节能调度方面的拓展.
基于以上分析发现, 目前尚未出现同时考虑工时阶梯恶化与能耗的并行机调度优化研究. 现有并行机调度算法在处理实际约束时存在大规模算例计算时间过长、算法收敛速度慢、求解质量不高等问题, 且难以将工作模式选择考虑进去. 本文针对有温度要求的工件, 在等待加工的过程中有保温或者再加热两种方式, 均需消耗一定能量. 再加热还会导致其加工时间发生恶化. 以尿素厂造粒塔为研究背景, 提出以加权总拖期与总能耗之和最小化为调度目标的工时阶梯恶化并行机调度问题. 通过分析问题构建了混合整数线性规划模型, 由于问题的NP-hard特性, 提出了遗传变邻域混合搜索算法(Genetic Algorithm-Variable Neighborhood Search, GA-VNS). 通过集成遗传算法(Genetic Algorithm, GA)与变邻域搜索(Variable Neighborhood Search, VNS)的优势有效实现了对问题的求解. 通过算例计算结果, 验证了该算法在解决较大规模算例时的效率.
1 问题描述与数学建模给定机器集合
| $ {e_j} = {e_0} \times \max \{ 0,{s_j} - {h_j}\} $ | (1) |
式中,
调度决策就是指派工件到各台机器, 同时选择恰当的工作模型以保证工件能够顺利完工, 以求最小化总拖期时间与加工能耗. 表1解释了本文数学模型中的变量和符号. 所提出的混合整数规划模型如下:
目标函数为:
| $ F(X,Y,Z,U) = \alpha \sum\limits_{j \in N} {{T_j}} + \beta \sum\limits_{j \in N} {{E_j}} $ | (2) |
约束条件为:
| $ \sum\limits_{k \in M} {{y_{jk}} = 1} \;\;\;\;\;\;\;\;\forall j \in N $ | (3) |
| ${y_{ik}} + {y_{jk}} \le 1 + {x_{ij}} + {x_{ji}}\;\;\;\;\;\;\;\;\forall i,j \in N,i \ne j,k \in M $ | (4) |
| $ {c_i} - {s_j} \le M(1 - {x_{ij}})\;\;\;\;\;\;\;\;\forall i,j \in N $ | (5) |
| $ {s_j} + {p_j} \le {c_j}\;\;\;\;\;\;\;\;\forall j \in N $ | (6) |
| $ {c_j} - {d_j} \le {T_j}\;\;\;\;\;\;\;\;\forall j \in N $ | (7) |
| $ {a_j} \le {p_j} \le {a_j} + {b_j}\;\;\;\;\;\;\;\;\forall j \in N $ | (8) |
| $ {s_j} \le {h_j} + M(1 - {{\textit{z}}_j})\;\;\;\;\;\;\;\;\forall j \in N $ | (9) |
| $ {u_j} \le 1 - {{\textit{z}}_j}\;\;\;\;\;\;\;\;\forall j \in N $ | (10) |
| $ {a_j} + {b_j}(1 - {u_j}-{{\textit{z}}_j}) \le {p_j}\;\;\;\;\;\;\;\;\forall j \in N $ | (11) |
| $ {e_0} \times ({s_j} - {h_j}) - M(1 - {u_j}) \le {e_j}\;\;\;\;\;\;\;\;\forall j \in N $ | (12) |
| $ {e_j} + {p_j} \times {q_j} \le {E_j}\;\;\;\;\;\;\;\;\forall j \in N $ | (13) |
| $ {x_{ij}},{y_{ik}},{x_{ik}} \in \{ 0,1\} \;\;\;\;\;\;\;\;\forall i,j \in \Omega ,k \in \Omega $ | (14) |
| $ {e_j},{T_j},{E_j},{s_j} \ge 0\;\;\;\;\;\;\;\;\forall j \in \Omega $ | (15) |
上述模型中, 目标函数(2)为最小化所有工件的加权总拖期与总能耗之和, 其中
| 表 1 数学模型中的符号 |
2 遗传变邻域混合搜索算法
由于考虑工时阶梯的单机总拖期问题已被证明为NP-hard的[22], 本文所考虑的问题为并行机加工环境且考虑能耗, 因此其也是NP-hard的. 随着工件数的增加, 很难通过精确的算法获得问题的最优解. 在大规模问题求解寻找近优解时, 群集智能优化算法求解效率明显高于精确求解方法. 遗传算法能够利用群集效应进行寻优, 具有先天的并行搜索能力, 故本文利用遗传算法的这一特性进行大规模问题的求解. 前期计算结果表明, 若仅仅使用基本遗传算法求解本文所提并行机调度问题, 易陷入局部最优解且求解效率相对较差. 在此采用混合变邻域搜索策略来提高算法性能. 使用遗传算法经过一定迭代次数操作后的种群输出的最优染色体做为初始解, 进一步实施变邻域搜索, 以达到提高算法质量, 提升运算效率的目的. 因此, 本文针对所提并行机调度问题的特性, 集成考虑遗传算法和变邻域搜索的优势, 提出了基于遗传算法框架的遗传变邻域混合搜索算法.
2.1 编码和解码方式编码是整个算法的第一步, 对算法效果有巨大影响. 本文的编码方式必须满足两方面的需求, 一是要确定机器的指派问题, 另一个则是要确定每台机器上工件的加工顺序. 本算法采用实数编码方式. 每个解序列为从1到
初始化种群是本文整个算法的开端, 其组成结构对整个算法影响很大. 本文采用随机生成的方式生成初始种群, 以保证染色体可取到所有的可能调度序列.

|
图 1 染色解码方式甘特图表示 |
2.2.2 适应度函数
模型目标是最小化所有工件的加权总拖期与总能耗之和, 因此本文的适应度函数为目标函数的倒数:
| $ f({\pi _i}) = 1/(\alpha T({\pi _i}) + \beta E({\pi _i})) $ | (16) |
其中,
选择的作用是可以从当前群体中选出优良个体, 使得好的个体有更大的机会保留下来并将其优良的信息传递给下一代, 因而可以逐步地向最优解逼近. 本文的选择操作选用轮盘赌选择方法, 染色体被选中的概率L为:
| $ L({\pi _i}) = \frac{{\alpha T({\pi _i}) + \beta E({\pi _i})}}{{\displaystyle\sum\limits_{i = 1}^{{p_{\rm num}}} {\alpha T({\pi _i}) + \beta E({\pi _i})} }} $ | (17) |
在式(17)中,
交叉操作是种群中产生新个体的主要步骤, 好的交叉方法对于遗传算法的效果也有显著影响. 由于顺序交叉能够在保留原有排列的基础上融合不同排列的有序结构单元, 本文选用两点顺序交叉(类OX), 顺序交叉的具体流程(图2)如下:
步骤1. 父代1和父代2配对, 从父代1中随机选择一段连续的基因, 并将这段基因按顺序放在子代1的起始部分;
步骤2. 去除父代2中包含父代1被选基因段的基因;
步骤3. 将父代2中去除父代1备选基因段后剩余的基因按顺序依次填入子代1的剩余位置. 此时, 获得了完整的子代1的基因.
同理, 按照以上步骤, 可从父代2中随机选取一部分基因段和父代1中的出去被选基因段部分, 按照上述步骤插入得到子代2.

|
图 2 类OX交叉示意图 |
2.2.5 变异操作
当遗传算法通过交叉算子已接近最优邻域解时, 利用变异操作可以提高其随机搜索能力, 且可以有效维持群体多样性. 本文选用随机位置交换完成变异操作. 随机选中两个元素进行位置调换即完成变异操作. 如图3示例: 父代

|
图 3 随机选择变异示意图 |
2.3 变邻域搜索
变邻域搜索算法[14]通过搜索多个邻域结构能够较好的避免陷入局部最优解, 是一种改进型的局部搜索算法. 本文对使用遗传算法经过一定迭代次数操作后的最优染色体进行变邻域搜索操作, 以进一步改善解的质量.
变邻域搜索算法的工作原理是通过各种邻域结构对当前解实施变换, 以产生可行解集合. 目前关于调度问题的邻域结构大多数是基于插入和交换操作. 除了这些基本的邻域结构, 本文还引入了逆序操作. 因此, 本节使用插入和交换操作构造4种邻域结构, 并使用逆序定义了一种邻域结构. 以下将分别对这5种邻域结构进行介绍.
邻域搜索结构(Neighborhood Search) NS1和NS2原理相似. 两者均是其中利用交换对当前解实施微小的变动. 区别在于NS1是从整个解序列的第一个元素开始到最后一个元素结束, 依次随机选择一个与其不相等的元素进行交换, 也就是把解序列内的所有元素都与其他不重复的随机位置进行交换, 而NS2则是在解序列中随机选择一个元素, 将其插入到另一个不重复的随机选定的元素上. 在NS1和NS2的操作过程中只要解的质量比原来的解好, 立即接受其为当前解, 并重新开始搜索; 否则继续搜索直至所有可能的组合均已完成.
邻域搜索结构NS3和NS4有着类似的操作. 两者和NS1, NS2不同的是NS3和NS4所进行的交换操作是两两交换, 即同时交换的元素有4个, 成对交换. NS3从解序列的前两个元素开始到最后两个元素结束, 依次选择两个元素与另外随机选择的两个不重复的元素分别进行交换. 与NS1和NS2的区别一样, NS4则是随机的取两个元素与另外一对两个随机的不重复的元素分别进行交换. 其实施过程与NS3相同. 一旦发现给出的邻域解有所改善, 则将该邻域解视为当前解, 并再次开始搜索更好的解; 否则继续搜索直至搜索完成所有的邻域结构.
为了进一步提高算法的性能, 基于逆序操作的邻域结构NS5在上述4个邻域完成后实施. NS5的具体操作为: 从当前解序列中随机选择两个元素, 将两者之间的工件全部逆序, 以形成新的解. 该步骤重复n+m–1次以寻找较好的解. 与前4个邻域结构一样, 该邻域结构只接受效果更好的解.
2.4 GA-VNS算法框架通过使用2.3节的5种邻域搜索结构, 再结合2.2节的遗传算法为VNS算法提供初始解, 即可对本文提出的问题实施GA-VNS算法. GA-VNS的终止条件为: (1)达到最大迭代次数

|
图 4 GA-VNS程序框图 |
3 算例验证
本章采用两组算例验证算法的性能, 具体的参数取值见3.1节. 所提出的遗传变邻域混合搜索算法将在3.2节对算法关键参数进行参数调试. 本节对比了Gurobi、GA、VNS[14]和GA-VNS对小规模和大规模算例的计算效果, 以验证所提算法性能. 本节所涉及的所有算法均在Visual Studio 2013平台使用C#语言编程实现, 在CPU (Intel 3.6 G)/RAM (8 GB)的个人计算机上运行. 为了方便分析算法的性能, 本节将求解得到的目标函数转换成百分偏差, 用R作为参数分析的响应变量, 其值由式(18)决定.
| $ R = \frac{{obj(Alg ) - obj(Best)}}{{obj(Best)}} \times 100\% $ | (18) |
式(18)中,
本节采用两组算例来验证算法性能. 其中小规模算例的工件数
需要注意的是, Gurobi、GA和VNS实验数据也是来源于此. GA的算法结构采用本文遗传算法部分的结构, VNS的算法结构采用本文变邻域搜索部分的内容. 设定Gurobi运算时间为3600 s, 如果在给定的时间内没有找到最优解, 则返回当前已发现的最好整数解. 关于GA和VNS算法的终止条件, 它们的最大循环次数
算法求解的质量和算法参数的选择息息相关, 本文所提GA-VNS算法所涉及的主要参数为: 用作GA-VNS算法初始解的遗传算法的交叉概率
在GA-VNS算法中, 使用工件数为40机器数为6的大规模算例对每个参数都进行10次求解运算, 并对其求解结果实施单因素方差分析(ANOVA). 为了方便分析不同取值水平下GA-VNS算法的效果, 图5至图7分别给出了3个参数不同取值的均值图和95% 置信水平下的Tukey真实著性差异(Honestly Significant Difference, HSD)区间.
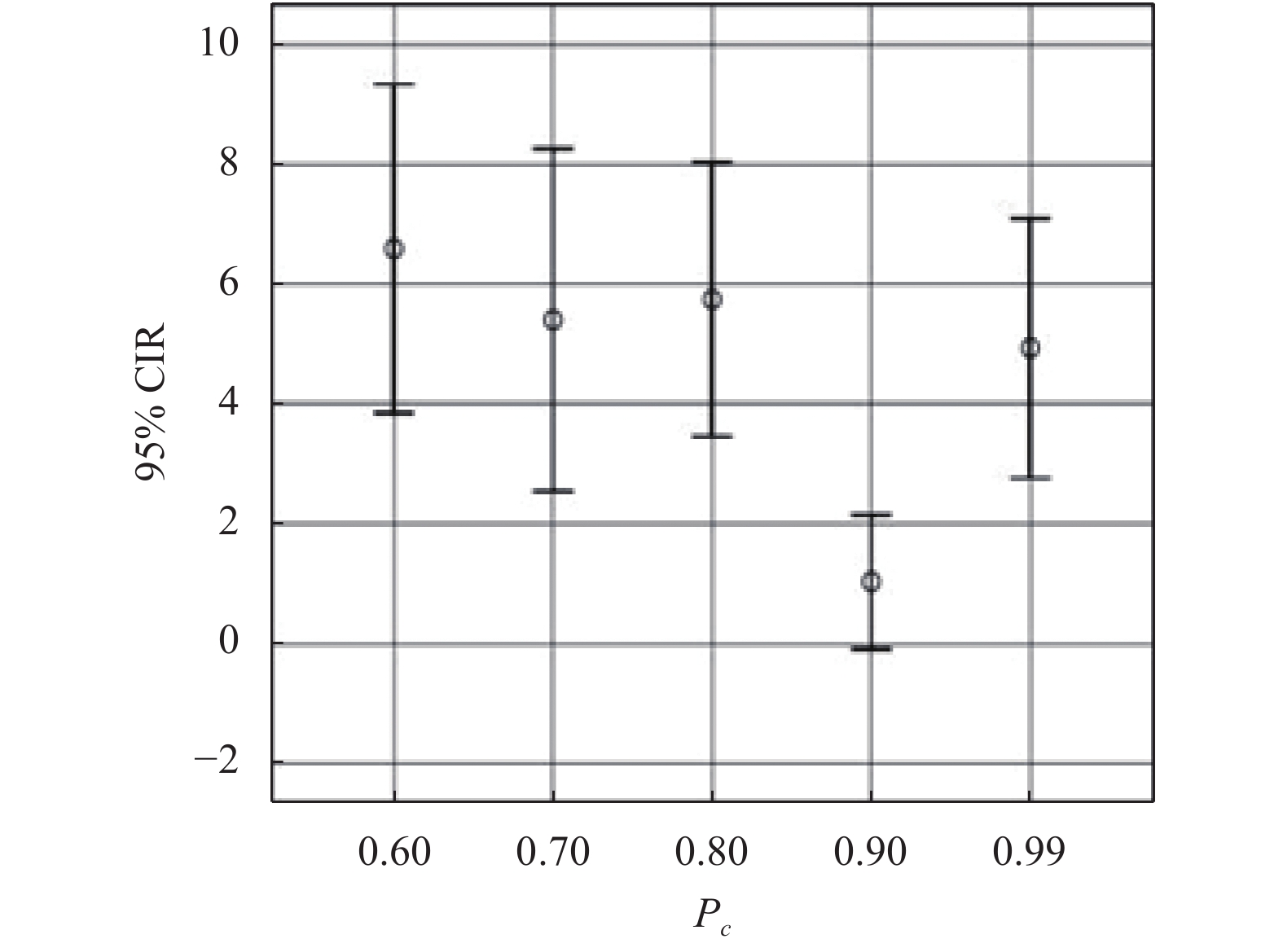
|
图 5 不同
|

|
图 6 不同
|

|
图 7 不同
|
从图5可以看出, 交叉概率
在本节的计算中, 同一组算例运算10次, 取平均值的整数部分, 保留R值的小数后两位与平均运行时间的小数后3位为最终运算结果. 对比了Gurobi、GA、GA-VNS和VNS对小规模算例和大规模算例的运算结果.
表2列出了各个算法求解小规模算例的计算结果. 从表2中可以看出, GA-VNS和Gurobi都能给出所有小规模算例的最好结果, 且其解效果十分稳定. 从计算时间上来看, GA-VNS的平均计算时间为0.232 s, 且只有工件数为12, 机器数为4的算例计算时间超过1 s, 其余均低于1 s. 而Gurobi的平均计算时间为1.166 s,这说明在求解质量相同的情况下, GA-VNS的求解效率要好于Gurobi. GA和VNS的计算时间比起GA-VNS来说相差无几, 但是两者的求解质量却不及GA-VNS. 由表2可以看到, 在全部15个小规模算例中, VNS只给出了8个算例的最优解, 平均R值为0.804. 与VNS相比, GA给出了13个算例的最优解, 平均R值为0.107, 优于VNS, 但还是不如GA-VNS给出的解的质量好. 从基于小规模算例的计算结果可以看出, GA-VNS表现出了最好的求解性能.
使用Gurobi、GA、VNS和GA-VNS求解大规模算例, 计算结果见表3. 由于问题的难求解性, Gurobi仅能给出机器数为6工件数为20、机器数为8工件数为20以及机器数为8工件数为40的近似最优解. 并且在求解所有大规模算例时, 均耗光了计算时间都未找到最优解, 且还有12个算例未找到可行解. 总体来讲, Gurobi求解大规模算例的效果并不理想. GA-VNS给出的平均R值为0.007, 明显优于Gurobi和另外两个启发式算法. 除了机器数为6, 工件数为100这一算例外, 其余算例的最优值Best均由GA-VNS给出. 在3种启发式算法中, GA-VNS由于引入GA输入初始解和变邻域搜索结构, 使得其平均计算时间最长, 平均计算时间为3.142 s. 但考虑到GA-VNS优良的求解性能, 付出的计算时间还是可以接受的. 相比之下, GA的运算时间是最短的, 其平均计算时间为0.689 s. 但从表3可明显看出, 虽然GA的求解时间是最短的, 但其求解效果在3个启发式算法中却是最差的, 平均R值达到了38.233, 说明其求解精度还有很大的提高空间. VNS的平均计算时间和GA-VNS相差不大, 为2.994 s, 但在15个大规模算例中, VNS仅给出了一个最好的Best值, 平均R值为5.24, 且随着工件数的增加, 其R值也有逐渐增大的趋势. 总的来说, GA-VNS在较短的时间内给出了不错的近似最优解, 能够有效解决同时考虑工时阶梯恶化与能耗的并行机调度问题.
| 表 2 小规模算例计算结果 |
| 表 3 大规模算例计算结果 |
4 结论与展望
本文针对尿素造粒塔生产过程, 提出了一类考虑工时恶化和能耗的并行机调度问题, 建立了优化目标为加权总拖期与总能耗的混合整数线性规划模型. 由于问题的难求解性以及工作模式选择的特殊性, 本文提出了基于遗传算法框架的改进的遗传变邻域混合搜索算法. 采用了单因素方差分析确定关键算法参数, 并基于随机产生的两组算例, 分析了算法的性能. 与数学求解器Gurobi、基本的遗传算法与基本的变邻域搜索算法的计算结果做了对比, 结果验证了本文所提算法的可行性与高效性. 后续研究可引入动态规划对两类模式进行选择, 考虑结合更切合尿素造粒塔的实际生产情况的真实数据优化问题, 同时设计多目标的求解算法, 把两个优化目标单独研究.
| [1] |
吴国忠, 白浩然, 杨显志, 等. 尿素造粒塔内热环境仿真研究. 当代化工, 2014, 43(6): 975-977, 993. DOI:10.3969/j.issn.1671-0460.2014.06.035 |
| [2] |
付亚平, 黄敏, 王洪峰, 等. 混合并行机调度问题的多目标优化模型及算法. 控制理论与应用, 2014, 31(11): 1510-1516. DOI:10.7641/CTA.2014.31233 |
| [3] |
Li K, Yang SL. Non-identical parallel-machine scheduling research with minimizing total weighted completion times: Models, relaxations and algorithms. Applied Mathematical Modelling, 2009, 33(4): 2145-2158. DOI:10.1016/j.apm.2008.05.019 |
| [4] |
孟磊磊, 张超勇, 詹欣隆, 等. 不相关并行机节能调度问题建模. 中国机械工程, 2018, 29(23): 2850-2858. DOI:10.3969/j.issn.1004-132X.2018.23.012 |
| [5] |
周炳海, 顾佳颖. 考虑多资源约束的非等效并行机节能调度算法. 东北大学学报(自然科学版), 2019, 40(3): 403-408. DOI:10.12068/j.issn.1005-3026.2019.03.019 |
| [6] |
雷德明, 潘子肖, 张清勇. 多目标低碳并行机调度研究. 华中科技大学学报(自然科学版), 2018, 46(8): 104-109. DOI:10.13245/j.hust.180820 |
| [7] |
Li ZT, Yang HD, Zhang SQ, et al. Unrelated parallel machine scheduling problem with energy and tardiness cost. The International Journal of Advanced Manufacturing Technology, 2016, 84(1–4): 213-226. DOI:10.1007/s00170-015-7657-2 |
| [8] |
王永琦, 吴飞, 江潇潇, 等. 求解并行机拖期与能耗成本优化调度的混合教—学算法. 计算机应用研究, 2019, 36(3): 673-676. DOI:10.19734/j.issn.1001-3695.2017.09.0929 |
| [9] |
郭鹏, 程文明, 张则强. 求解具有恶化工件单机调度问题的改进遗传算法. 西南交通大学学报, 2011, 46(3): 506-511. DOI:10.3969/j.issn.0258-2724.2011.03.025 |
| [10] |
Ji M, Cheng TCE. Parallel-machine scheduling of simple linear deteriorating jobs. Theoretical Computer Science, 2009, 410(38–40): 3761-3768. DOI:10.1016/j.tcs.2009.04.018 |
| [11] |
Wang XY, Zhou ZL, Ji P, et al. Parallel machines scheduling with simple linear job deterioration and non-simultaneous machine available times. Computers & Industrial Engineering, 2014, 74: 88-91. DOI:10.1016/j.cie.2014.05.003 |
| [12] |
Guo P, Cheng WM, Wang Y. Parallel machine scheduling with step-deteriorating jobs and setup times by a hybrid discretecuckoo search algorithm. Engineering Optimization, 2015, 47(11): 1564-1585. DOI:10.1080/0305215x.2014.982634 |
| [13] |
Guo P, Cheng WM, Zeng M, et al. Scheduling step-deteriorating jobs on parallel machines by mixed integer programming. Journal of Donghua University (English Edition), 2015, 32(5): 709-714, 719. |
| [14] |
Cheng WM, Guo P, Zhang ZQ, et al. Variable neighborhood search for parallel machines scheduling problem with step deteriorating jobs. Mathematical Problems in Engineering, 2012, 2012: 928312. DOI:10.1155/2012/928312 |
| [15] |
Lalla-Ruiz E, VOß S. Modeling the parallel machine scheduling problem with step deteriorating jobs. European Journal of Operational Research, 2016, 255(1): 21-33. DOI:10.1016/j.ejor.2016.04.010 |
| [16] |
Pei J, Wang XM, Fan WJ, et al. Scheduling step-deteriorating jobs on bounded parallel-batching machines to maximise the total net revenue. Journal of the Operational Research Society, 2019, 70(10): 1830-1847. DOI:10.1080/01605682.2018.1464428 |
| [17] |
轩华, 秦莹莹, 王薛苑, 等. 带恶化工件的不相关并行机调度优化. 系统仿真学报, 2019, 31(5): 919-924. DOI:10.16182/j.issn1004731x.joss.17-0150 |
| [18] |
Yin YQ, Wang Y, Cheng TCE, et al. Parallel-machine scheduling of deteriorating jobs with potential machine disruptions. Omega, 2017, 69: 17-28. DOI:10.1016/j.omega.2016.07.006 |
| [19] |
Arık OA, Toksarı MD. Multi-objective fuzzy parallel machine scheduling problems under fuzzy job deterioration and learning effects. International Journal of Production Research, 2018, 56(7): 2488-2505. DOI:10.1080/00207543.2017.1388932 |
| [20] |
Lu SJ, Liu XB, Pei J, et al. A hybrid ABC-TS algorithm for the unrelated parallel-batching machines scheduling problem with deteriorating jobs and maintenance activity. Applied Soft Computing, 2018, 66: 168-182. DOI:10.1016/j.asoc.2018.02.018 |
| [21] |
郭鹏. 具有分段恶化效应生产过程的智能优化调度研究[博士学位论文]. 成都: 西南交通大学, 2014.
|
| [22] |
Guo P, Cheng WM, Wang Y. Scheduling step-deteriorating jobs to minimise the total weighted tardiness on a single machine. International Journal of Systems Science: Operations & Logistics, 2017, 4(2): 92-107. DOI:10.1080/23302674.2015.1084393 |
 2001, Vol. 29
2001, Vol. 29


