Stewart微动平台由动平台、定平台和连杆通过铰链链接而成, 可以实现6自由度运动. 作为一种并联机器结构, 具有结构刚度大、位置精度高、载重比高等优点, 被广泛应用于电子元件生产中的夹持系统、精密机床中的刀具控制和钻铣等领域. Stewart平台具有运动空间小、鲁棒性强、惯性小、运动精度高以及成本较低等优点, 同时具有较大的刚度和良好的定位能力, 是串联机构所不能代替的. 从Stewart平台的控制方面看, Stewart平台包含两个最基本的问题: 位姿正解和位姿反解. 位姿反解即Stewart的运动学反解是已知求解平台的位姿, 即已知3个线性坐标X、Y、Z和3个旋转坐标参量
目前, 位姿正解的求解方法主要有数值法和解析法两种. 数值法[4-7]采用迭代法进行求解, 迭代法对迭代初值的要求较高, 初值选择不当会导致迭代无法正常收敛, 从而无法获得正确解. 解析法[8-10]是通过构建多组约束方程并消去未知数的方法, 该法的求解过程较复杂、消元方法不确定, 同时求解过程慢, 无法满足实时控制的要求. 近年来, 基于智能算法的位姿正解方法引起学者的关注, 刘伟锐等提出采用一种改进的粒子群算法求解并联机构的位姿正解[11]. 张宗之等[12]采用BP神经网络来对Stewart平台进行位姿正解, 收敛速度较慢, 容易陷入局部极值.
为了改进迭代法和解析法的缺点, 首先建立Stewart平台支腿长度与平台位姿的运动学模型, 然后利用Elman神经网络来实现位姿正解的求解并实验验证. 该方法具有良好的动态特性[13], 精度高, 能够快速准确的实现Stewart平台位姿正解的求解.
1 Stewart平台运动学模型Stewart平台结构如图1所示, 驱动器利用万向节和平台、底座链接, 通过伸缩运动驱动动平台运动, 从而在三维空间中实现6自由度的运动[14].

|
图 1 Stewart平台结构图 |
建立动坐标系Op-
XpYpZp和静坐标系O-XYZ. 两坐标系原点分别为动、静平台的质心, 坐标平面
在对平台进行控制时, 涉及到从任务空间至关节空间的转换, 任务空间采用位姿
| $\left\{ \begin{array}{l} {R_{\rm Z}}\left( \gamma \right) = \left[ {\begin{array}{*{20}{c}} {\cos\gamma }&{ - \sin\gamma }&0\\ {\sin\gamma }&{\cos\gamma }&0\\ 0&0&1 \end{array}} \right]\\ {R_{\rm Y}}\left( \beta \right) = \left[ {\begin{array}{*{20}{c}} {\cos\beta }&0&{\sin\beta }\\ 0&1&0\\ { - \sin\beta }&0&{\cos\beta } \end{array}} \right]\\ {R_{\rm X}}\left( \alpha \right) = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos\alpha }&{ - \sin\alpha }\\ 0&{\sin\alpha }&{\cos\alpha } \end{array}} \right] \end{array}\right. $ |
动平台相对于定平台的旋转矩阵为:
| $ \begin{aligned} R & = {R_{\rm Z}}\left( \gamma \right) \cdot {R_{\rm Y}}\left( \beta \right) \cdot {R_{\rm X}}\left( \alpha \right) \\ & = \left[ {\begin{array}{*{20}{c}} {C\beta C\gamma }&{S\alpha S\beta C\gamma - C\alpha S\gamma }&{C\alpha S\beta C\gamma + S\alpha S\gamma }\\ {C\beta S\gamma }&{S\alpha S\beta S\gamma + C\alpha C\gamma }&{C\alpha S\beta S\gamma - S\alpha C\gamma }\\ { - S\beta }&{S\alpha C\beta }&{C\alpha C\beta } \end{array}} \right] \end{aligned} $ | (1) |
计算长度时, 需要统一坐标系, 即通过转换矩阵将动坐标系
| $ T = \left[ {\begin{array}{*{20}{c}} {C\beta C\gamma }&{S\alpha S\beta C\gamma - C\alpha S\gamma }&{C\alpha S\beta C\gamma + S\alpha S\gamma }&{{x_p}}\\ {C\beta S\gamma }&{S\alpha S\beta S\gamma + C\alpha C\gamma }&{C\alpha S\beta S\gamma - S\alpha C\gamma }&{{y_p}}\\ { - S\beta }&{S\alpha C\beta }&{C\alpha C\beta }&{{{\textit{z}}_p}}\\ 0 & 0 & 0 & 1 \end{array}} \right] $ | (2) |
式中,
| ${\left[ {{P_{ix}}^{\rm{'}}{P_{iy}}^{\rm{'}}{P_{i{\textit{z}}}}^{\rm{'}}{\rm{}}1} \right]^{\rm T}} = T{\left[ {{P_{ix}}{P_{iy}}{P_{i{\textit{z}}}}{\rm{}}1} \right]^{\rm T}}$ | (3) |
根据支腿两端坐标, 可得支腿长度为:
| ${l_i}\!\! =\!\! \sqrt {{{\left( {{P_{ix}}^{'} \!\!-\!\! {O_{ix}}} \right)}^2}\!\! +\!\! {{\left( {{P_{iy}}^{'}\!\! -\!\! {O_{iy}}} \right)}^2} \!+\! {{\left( {{P_{i{\textit{z}}}}^{'} - {O_{i{\textit{z}}}}} \right)}^2}} ,\left( {i = 1,2, \cdots ,6} \right)$ | (4) |
从数学模型可见, 6条支腿长度
| $\left\{ {\begin{array}{*{20}{c}} {{f_1}\left( {x,y,{\textit{z}},\alpha ,\beta ,\gamma ,{l_1}} \right) = 0}\\ {{f_2}\left( {x,y,{\textit{z}},\alpha ,\beta ,\gamma ,{l_2}} \right) = 0}\\ {{f_3}\left( {x,y,{\textit{z}},\alpha ,\beta ,\gamma ,{l_3}} \right) = 0}\\ {{f_4}\left( {x,y,{\textit{z}},\alpha ,\beta ,\gamma ,{l_4}} \right) = 0}\\ {{f_5}\left( {x,y,{\textit{z}},\alpha ,\beta ,\gamma ,{l_5}} \right) = 0}\\ {{f_6}\left( {x,y,{\textit{z}},\alpha ,\beta ,\gamma ,{l_6}} \right) = 0} \end{array}} \right.$ | (5) |
对式(5)所示的方程组进行求解, 就可以得到平台的位姿参数, 即得到动平面对应的动坐标系Op-
XpYpZp原点
由式(5)可得, Stewart平台的模型是由6个多元非线性方程构成, 无法通过常规的公式推导进行简化和求解. 在实际应用中, 由于模型失配、测量误差等, 所建立的非线性方程组不完全守恒, 从而会造成求解失败的现象. Elman神经网络作为一种具有局部记忆单元和局部反馈连接的递归神经网络[10], 具有良好的动态特性, 收敛速度快, 因此, 基于Elman神经网络建立Stewart平台的位姿正解模型.
2 基于Elman神经网络的Stewart平台位姿正解Elman神经网络的网络结构一般分为4层: 输入层、输出层(中间层)、承接层和输出层. 输入层、隐含层、输出层的连接类似于前馈式网络, 输入层的单元仅起信号传输作用, 输出层单元起线性加权作用. 隐含层单元的传递函数可采用线性或者非线性函数, 承接层又称为上下文层或者状态层, 它用来记忆隐含层单元前一时刻的输出值并返回给网络的输入, 可以认为是一个一步延时算子. Elman神经网络的网络结构图如图2所示.
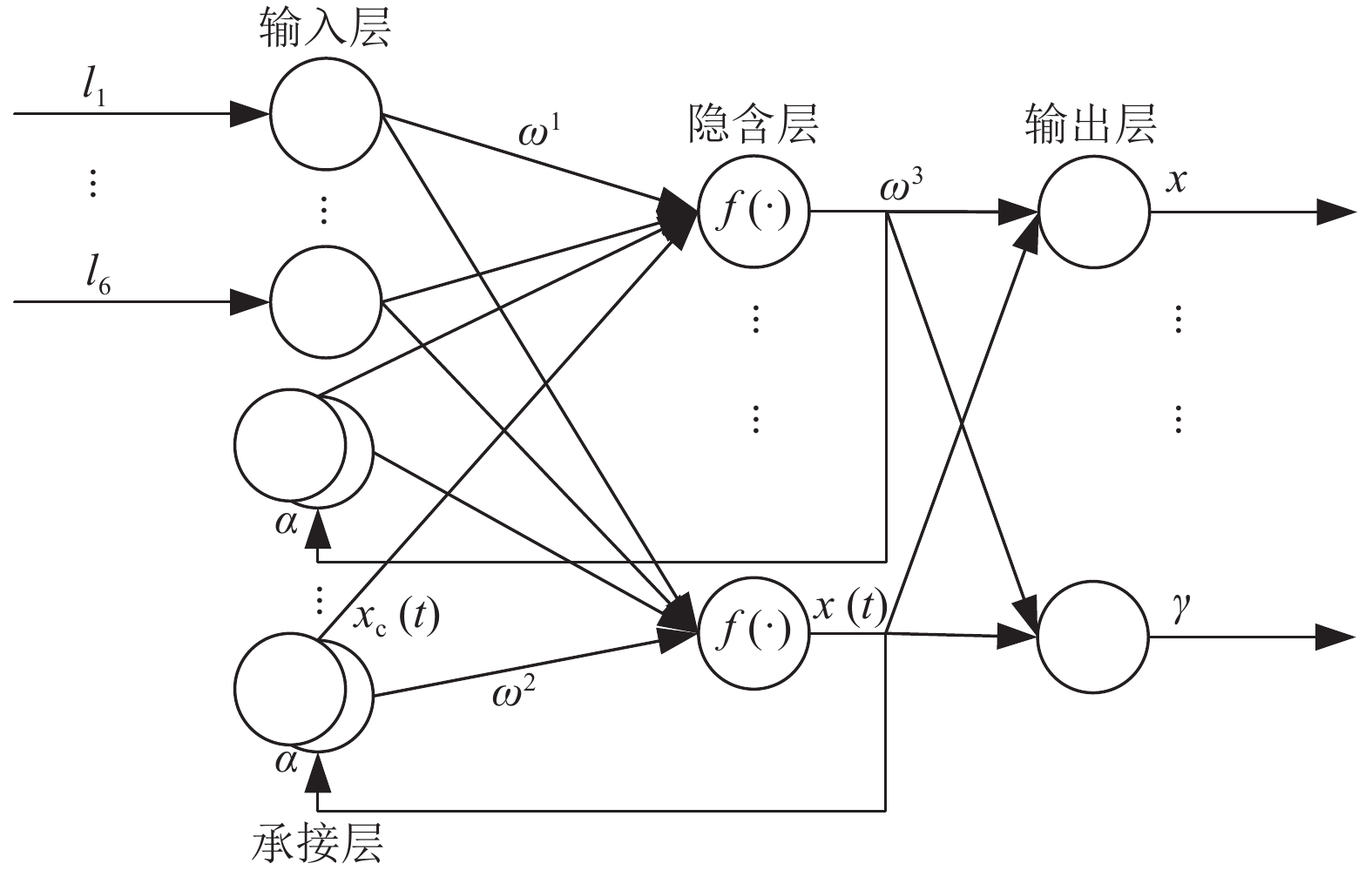
|
图 2 Elman神经网络结构图 |
采用Elman神经网络进行位姿正解时, 输入为6条支腿长度
数学模型可以表示为:
| $ x\left(k\right)=f\left({\omega }^{2}{x}_{c}\left(k\right)+{\omega }^{1}u(k-1)\right) $ | (6) |
| $ {x}_{c}\left(k\right)=\alpha {x}_{c}\left(k-1\right)+x(k-1) $ | (7) |
| $\hat y\left( k \right) = g\left( {{\omega ^3}x\left( k \right)} \right)$ | (8) |
其中,
Elman神经网络的输出可表示为:
| $\hat y\left( k \right) = {\omega ^3}x\left( k \right)$ | (9) |
学习指标函数为:
| $ E=\frac{1}{2}{\left(y\left(k\right)-\hat y\left(k\right)\right)}^{\rm T}\left(y\left(k\right)-\hat y\left(k\right)\right) $ | (10) |
神经网络的权重更新公式为:
| $ W\left(k+1\right)=W\left(k\right)+\eta \left(-\frac{\partial E}{\partial W}\right) $ | (11) |
其中,
学习指标E关于
| $ \frac{\partial E}{\partial {\omega }_{ij}^{3}}=-\left({y}^{i}\left(k\right)-{\widehat{y}}^{i}\left(k\right)\right)\frac{\partial {\widehat{y}}^{i}\left(k\right)}{\partial {\omega }_{ij}^{3}}=-{\varphi }_{i}^{o}{x}_{j}\left(k\right) $ | (12) |
其中,
同理, 学习指标E关于
| $ \frac{\partial E}{\partial {\omega }_{jl}^{2}}=\sum _{i=1}^{m}(-{\varphi }_{i}^{o}{\omega }_{ij}^{3})\frac{\partial {x}_{j}\left(k\right)}{\partial {\omega }_{jl}^{2}},\;\;l={1,2},\cdots ,n $ | (13) |
| $\begin{split} \dfrac{{\partial {x_j}\left( k \right)}}{{\partial \omega _{jl}^2}} &= \dfrac{\partial }{{\partial \omega _{jl}^2}}{f_j}\left( {\displaystyle \mathop \sum \limits_{l = 1}^n \omega _{jl}^2{x_{c,j}}\left( k \right)+ } {\displaystyle \mathop \sum \limits_{q = 1}^r \omega _{jq}^1{u_q}\left( {k - 1} \right)} \right)\\ &= f_j^{\rm{'}}\left( \cdot \right)\left( {{x_{c,j}}\left( k \right) + \displaystyle \mathop \sum \limits_{l = 1}^n \omega _{jl}^2\frac{{\partial {x_{c,j}}\left( k \right)}}{{\partial \omega _{jl}^2}}} \right) \end{split}$ | (14) |
若不考虑
| $ \frac{\partial {x}_{j}\left(k\right)}{\partial {\omega }_{jl}^{2}}={f}_{j}^{'}\left( \cdot \right){x}_{l}\left(k-1\right)+\alpha \frac{\partial {x}_{j}(k-1)}{\partial {\omega }_{jl}^{2}} $ | (15) |
同理, 学习指标E关于
| $ \frac{\partial E}{\partial {\omega }_{jq}^{1}}=\frac{\partial E}{\partial {\omega }_{j}\left(k\right)}\frac{\partial {x}_{j}\left(k\right)}{\partial {\omega }_{jq}^{1}}=-{\varphi }_{j}^{h}{u}_{q}(k-1) $ | (16) |
其中,
| $ {\varphi }_{j}^{h}=\sum \limits_{i=1}^{m}\left({\varphi }_{i}^{o}{\omega }_{ij}^{3}\right){f}_{j}^{'}\left( \cdot \right),q={1,2},\cdots ,r $ | (17) |
图3所示为本次的实验对象Stewart平台.

|
图 3 Stewart平台 |
3.1 Stewart平台参数
根据表1和表2的Stewart平台参数, 圆上任意一点坐标计算公式:
| $\left\{ {\begin{array}{*{20}{c}} {x' = r'*\cos\alpha '}\\ {y' = r'*\sin\alpha '} \end{array}} \right.$ | (18) |
其中,
| 表 1 Stewart平台尺寸参数 |
| 表 2 Stewart平台支腿连接点位置参数(单位: °) |
| 表 3 支腿动平台连接点坐标 |
| 表 4 支腿静平台连接点坐标 |
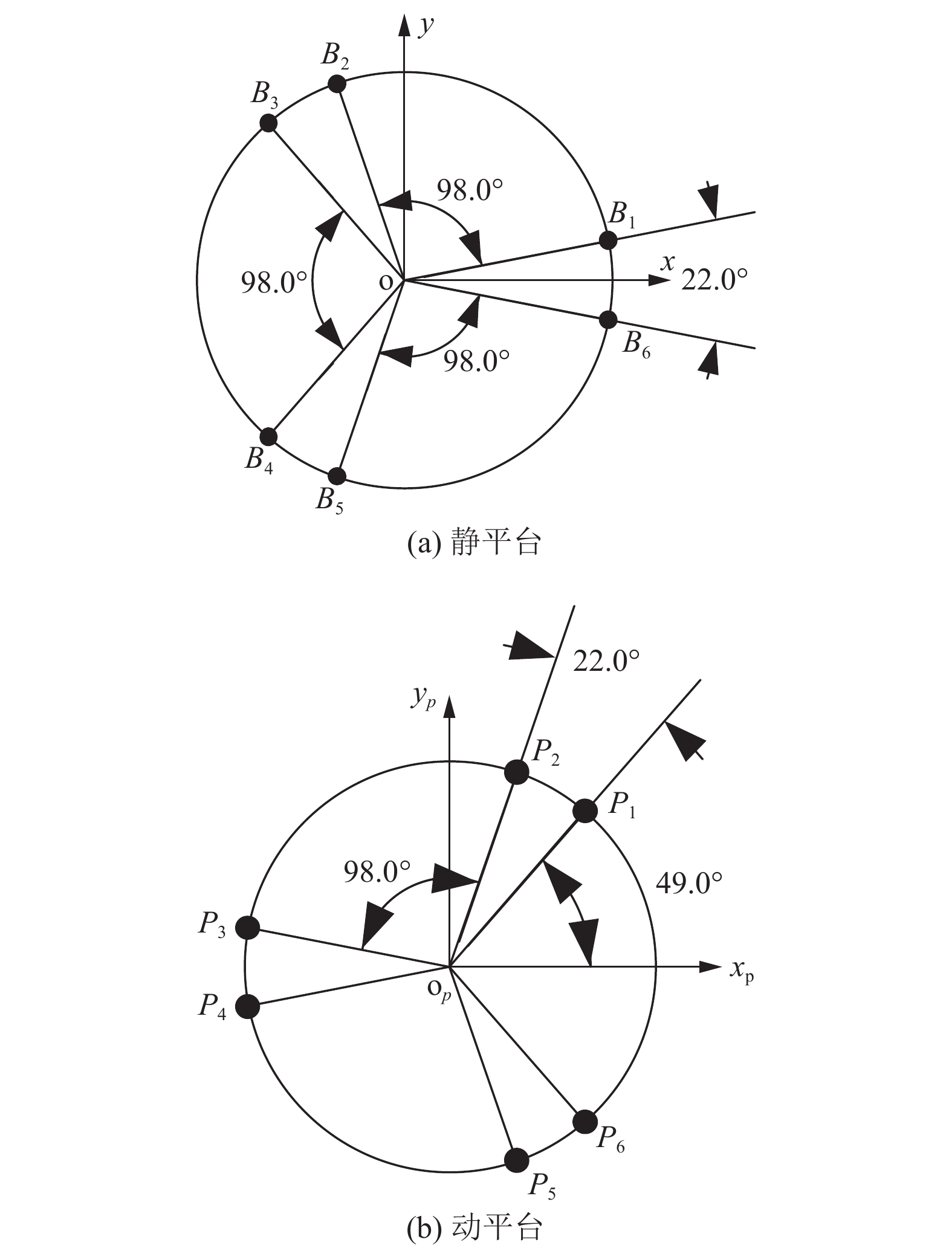
|
图 4 Stewart平台参数化模型 |
3.2 Elman神经网络训练及验证
Elman神经网络模型结构选择为6-5-6, 输入为支腿长度
根据表5, 可选取运动函数为:
| $ \left\{ {\begin{array}{*{20}{l}} {{f_{\rm X}}\left( t \right) = 20\sin t}\\ {{f_{\rm Y}}\left( t \right) = 20\sin t}\\ {{f_{\rm Z}}\left( t \right) = 10\sin t}\\ {{f_\alpha }\left( t \right) = 0.13\sin t}\\ {{f_\beta }\left( t \right) = 0.13\sin t}\\ {{f_\gamma }\left( t \right) = 0.21\sin t} \end{array}} \right. $ | (19) |
对应的6个支腿长度变化曲线如图5所示.
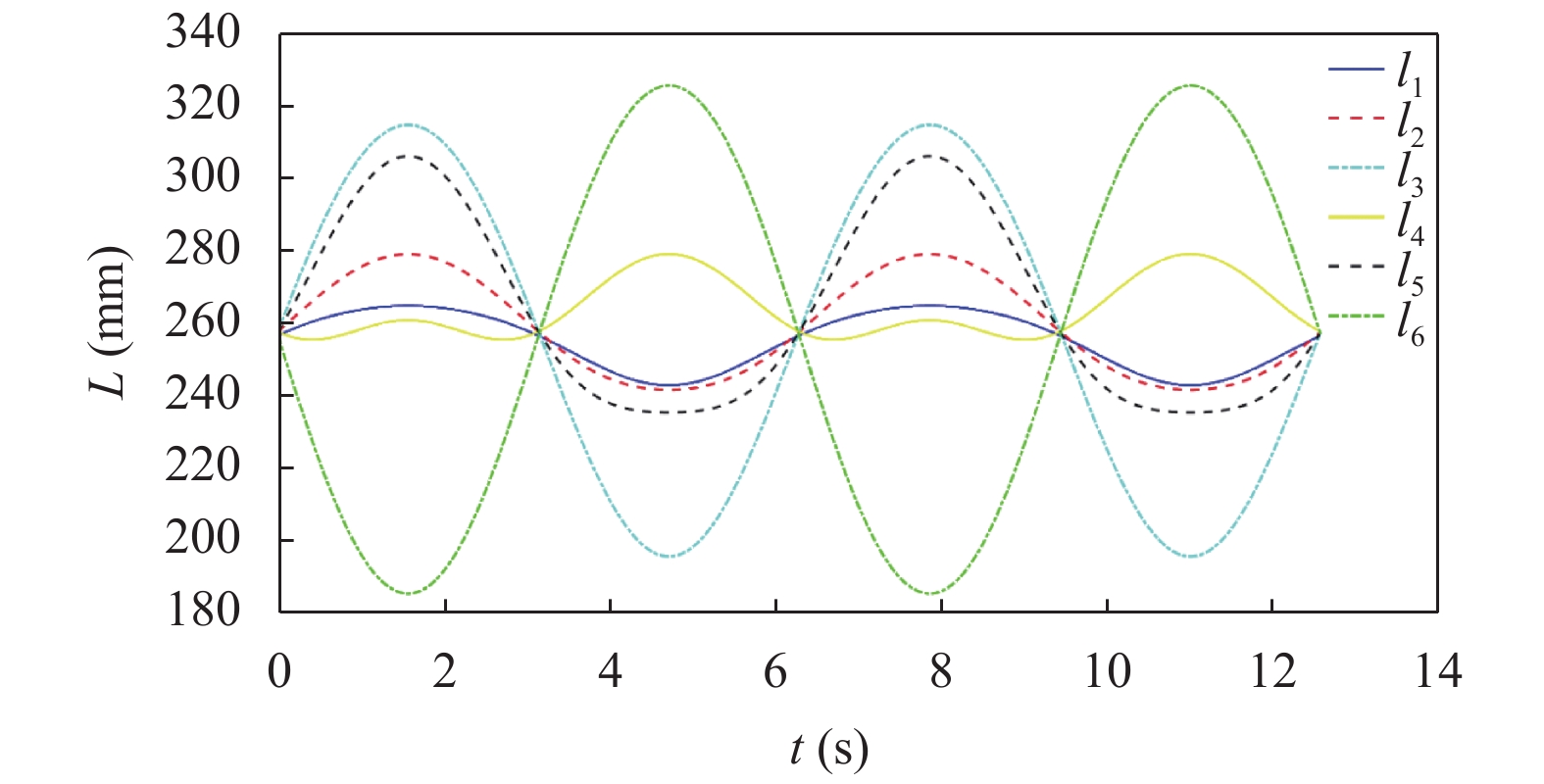
|
图 5 样本支腿长度变化图 |
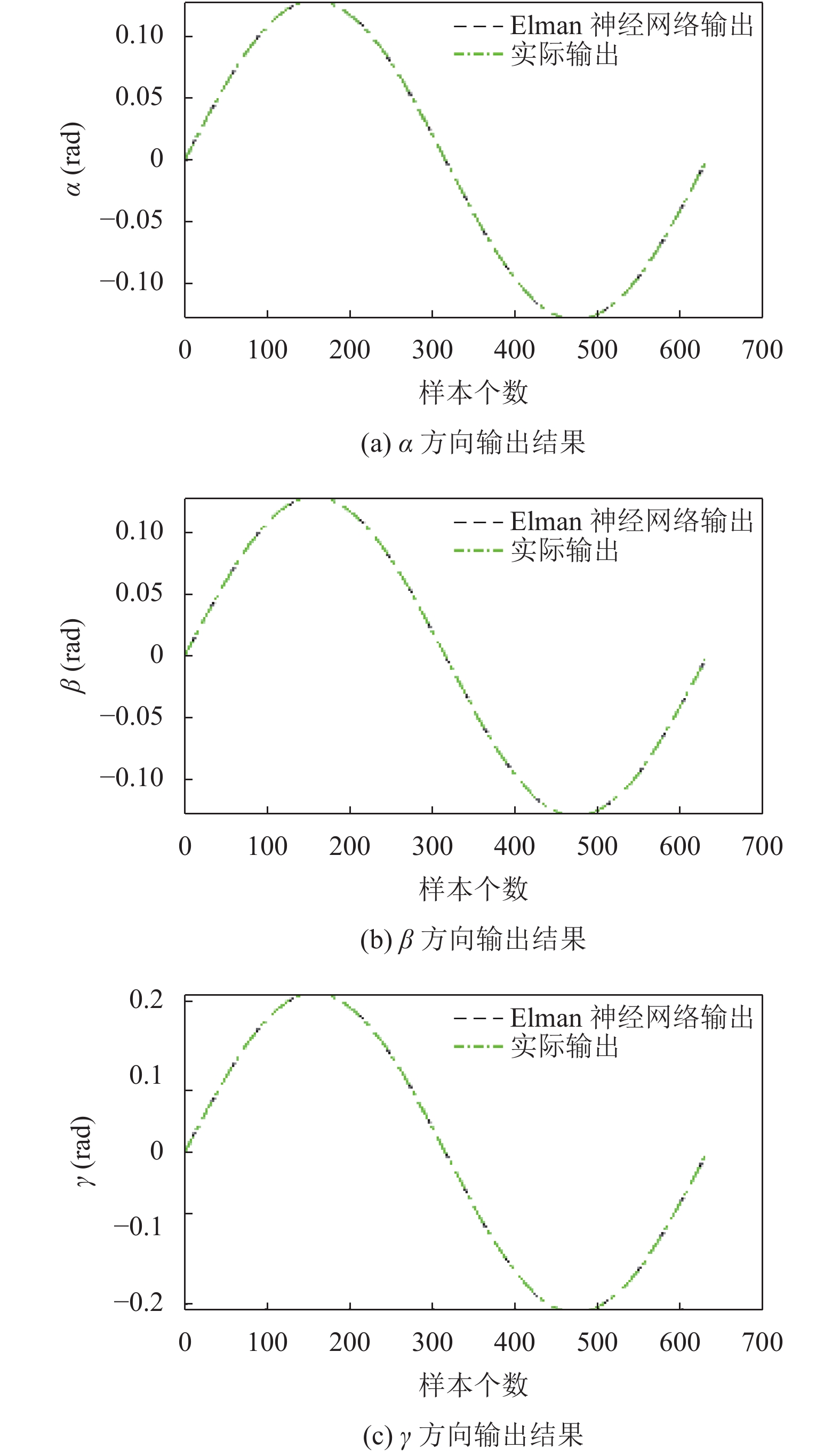
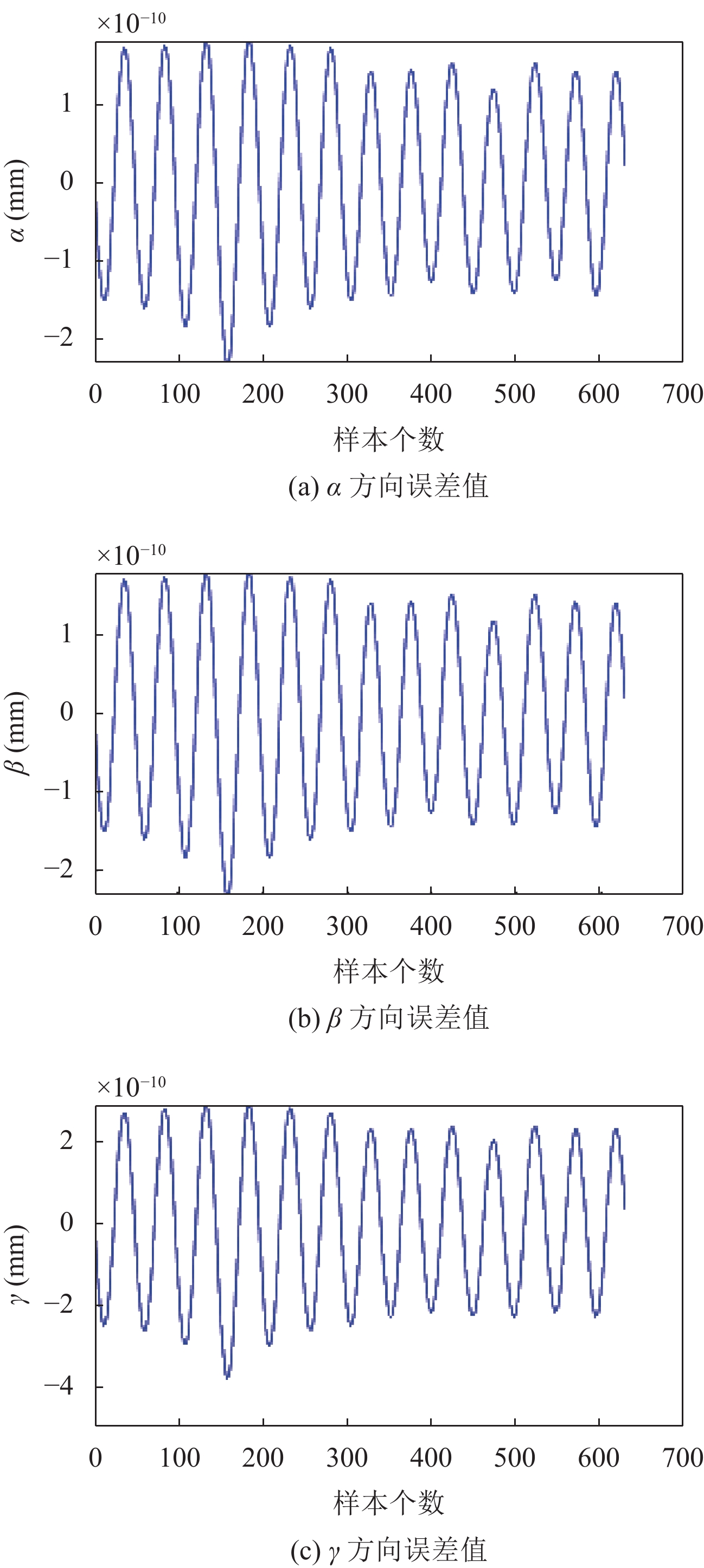
最终结果如图6与图7所示, 分别为X、Y、Z和α、β、γ方向上的Elman神经网络输出与实际输出图, 图中黑色虚线代表Elman神经网络输出, 绿色点虚线代表实际输出, 误差统计见表6. 图8与图9分别表示X、Y、Z和α、β、γ方向上的误差图.
| 表 5 Stewart平台运动范围参数 |
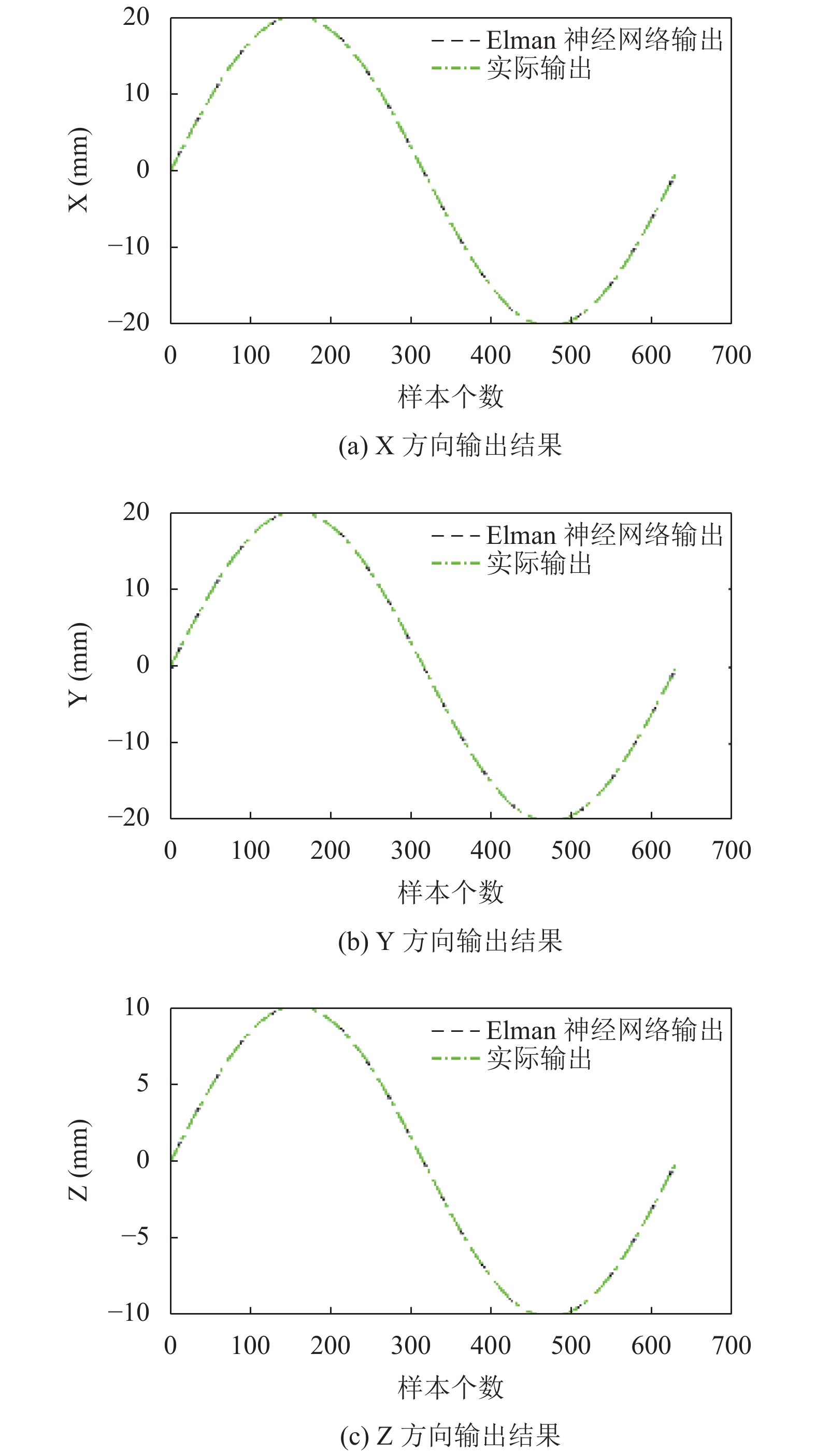
|
图 6 X、Y、Z输出结果 |
| 表 6 Elman神经网络输出结果误差统计 |
|
图 7 α、β、γ输出结果 |

|
图 8 X、Y、Z误差 |
4 结论
由于Stewart平台的位姿正解方程组由6个多元非线性方程构成, 普通方法难以得位姿正解. 更快更准确地求出其位姿有助于对Stewart平台的分析. 根据平台结构与其运动学模型建立了相应动平台与静平台坐标系, 用以描述支腿各连接点位置坐标和平台位姿, 通过坐标法表示运动位姿与支腿长度之间的关系. 建立了模型基于Elman神经网络的Stewart平台位姿正解模型, 对网络进行训练和实验验证. 实验结果表明: 基于elman神经网络的Stewart平台位姿正解方法对于Stewart平台的位姿正解问题效果良好, 位移误差和旋转角度误差范围都在10−7~10−9mm左右, 精准度高, 验证了该法的有效性.
|
图 9 α、β、γ误差 |
| [1] |
陈海龙, 汪伟, 王小兵, 等. Stewart平台六自由度位姿方程的改进数值解法研究. 机床与液压, 2014, 42(3): 47-50. DOI:10.3969/j.issn.1001-3881.2014.03.013 |
| [2] |
Lopes AM. Dynamic modeling of a Stewart platform using the generalized momentum approach. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(8): 3389-3401. DOI:10.1016/j.cnsns.2009.01.001 |
| [3] |
刘兴芳. 六自由度并联平台的运动学分析与结构参数优化[硕士学位论文]. 太原: 中北大学, 2018.
|
| [4] |
Nanua P, Waldron KJ, Murthy V. Direct kinematic solution of a Stewart platform. IEEE Transactions on Robotics and Automation, 1990, 6(4): 438-444. DOI:10.1109/70.59354 |
| [5] |
Yang JF, Xu ZB, Wu QW, et al. Dynamic modeling and control of a 6-DOF micro-vibration simulator. Mechanism and Machine Theory, 2016, 104: 350-369. DOI:10.1016/j.mechmachtheory.2016.06.011 |
| [6] |
Lee KM, Shah D. Kinematic analysis of a three degrees of freedom in-parallel actuated manipulator. Proceedings of 1987 IEEE International Conference on Robotics and Automation. Raleigh, NC, USA. 1987. 345–350.
|
| [7] |
Puglisi LJ, Saltaren RJ, Rey Portolés G, et al. Design and kinematic analysis of 3PSS-1S wrist for needle insertion guidance. Robotics and Autonomous Systems, 2013, 61(5): 417-427. DOI:10.1016/j.robot.2013.02.001 |
| [8] |
Sayevand K, Jafari H. On systems of nonlinear equations: Some modified iteration formulas by the homotopy perturbation method with accelerated fourth- and fifth-order convergence. Applied Mathematical Modelling, 2016, 40(2): 1467-1476. DOI:10.1016/j.apm.2015.06.030 |
| [9] |
Niu XM, Gao GQ, Liu XJ, et al. Dynamics and control of a novel 3-DOF parallel manipulator with actuation redundancy. International Journal of Automation and Computing, 2013, 10(6): 552-562. DOI:10.1007/s11633-013-0753-6 |
| [10] |
Mohammed AM, Li S. Dynamic neural networks for kinematic redundancy resolution of parallel Stewart platforms. IEEE Transactions on Cybernetics, 2016, 46(7): 1538-1550. DOI:10.1109/TCYB.2015.2451213 |
| [11] |
刘伟锐, 赵恒华. 改进粒子群算法在并联机构位置正解中的应用. 机械设计与制造, 2014(2): 181-183. DOI:10.3969/j.issn.1001-3997.2014.02.056 |
| [12] |
张宗之, 秦俊奇, 陈海龙, 等. 基于BP神经网络的Stewart平台位姿正解算法研究. 机械传动, 2015, 39(6): 54-57. |
| [13] |
Zhang Y, Wang XP, Tang HM. An improved Elman neural network with piecewise weighted gradient for time series prediction. Neurocomputing, 2019, 359: 199-208. DOI:10.1016/j.neucom.2019.06.001 |
| [14] |
Lin PP, She JH, Wu M, et al. Decoupling control for parallel robot based on equivalent-input-disturbance approach. Proceedings of 2017 29th Chinese Control and Decision Conference. Chongqing, China. 2017. 4895–4900.
|
 2001, Vol. 29
2001, Vol. 29


