目前的脱机手写识别技术可以精确高效地识别数字、英文字母和汉字[1-6], 却无法较好地处理具有复杂空间结构关系的手写数学算式. 已有的一些识别算法[7,8]可以实现简易的数学算式的判别, 但对于一些具有复杂空间组合及包含关系的手写算式, 不能有效地识别. Aly等[9]提出仅利用相邻字符之间的空间关系进行算式识别, 但对于特殊字符, 如小数点等, 没有独立的识别方法, 还需进一步考虑相邻字符的识别结果. Wang等[10]提出了一种基于编码-解码器框架的新型多模态注意网络, 用于手写数学算式识别, 该方法在CROHME 2014和CROHME 2016数据库上达到了54.05%和50.56%的识别准确率, 尚不能满足应用需求. Dai等[11]实现了一款基于少量训练集的脱机手写算式识别系统, 实验结果显示, 该系统的识别准确率为80%. 胡龙灿等[12]基于Android平台开发了一款手写数学算式识别系统, 但并未实现对识别的数学算式进行智能计算的功能.
鉴于以上研究成果不能较好地识别具有复杂空间组合及包含关系的脱机手写数学算式, 且不具备智能计算功能. 本文提出了一种基于多重几何特征和CNN的手写算式识别的解决方案, 可有效提高手写算式识别的准确率, 并以此为基础设计了手写算式识别系统, 解决了数学算式智能计算问题, 实现了手写算式的自动评阅, 可应用于中小学课堂.
1 相关工作 1.1 图像预处理图像预处理效果的好坏直接影响到字符识别的准确率. 本文采取的图像预处理步骤如图1所示.

|
图 1 图像预处理 |
原始图像来源于手机或平板电脑等数字拍照设备, 由于应用场景为各类中小学课堂, 学生拍照会出现角度倾斜、光照不均等情况. 预处理时, 首先基于顶点提取算法[13]对原始图像进行倾斜校正, 接着采用自适应的高斯阈值分割算法对倾斜校正图像进行二值化. 为有效去除图像噪声, 保证图像分割质量, 本文采用高斯去噪算法对二值化图像进行降噪操作, 并基于圆形膨胀算法连接图像中的断裂笔划, 生成原始图像的黑白图. 然后, 依据字符切分算法[14]对黑白图进行切分, 得到单个字符图像. 最后对字符图像进行重心归一化和尺寸归一化[15], 生成了28×28像素的目标图像.
1.2 数据准备本文在MNIST数据集的0~9十类数字字符的基础上, 新增了“+, –, ×, ÷, <, >, =, (, ), √”等10类常用数学符号. 收集了不同年龄段的学生和部分成人的手写体数据, 并以此为基础, 经平移、旋转、缩放、腐蚀、膨胀、加噪等数字图像处理算法, 形成了每类数学符号图像约为9000张, 总计92 429张的数学符号训练集. 并将其和MNIST数据集合并, 生成了手写数学算式的字符训练库EQU-MNIST, 该数据集包含20类手写字符, 合计162 429条数据.
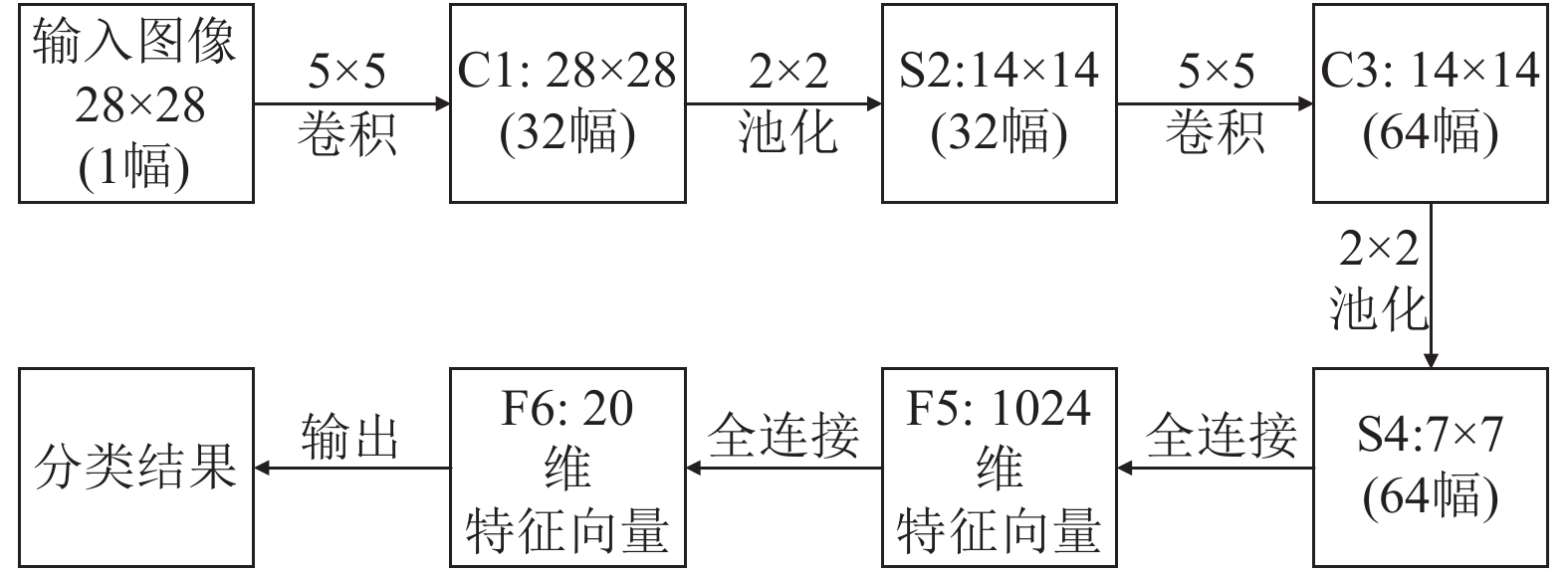
2 基于CNN的字符识别 2.1 字符识别文中用于单个字符识别的卷积神经网络结构[16]如图2所示, 网络模型包含两个卷积层、两个池化层和两个全连接层.
|
图 2 CNN模型 |
标准输入为一张28×28像素的图像. 第一层卷积层设定有32个5×5大小的卷积核, 输出32张28×28像素的特征图. 然后设定第一个池化层的大小为2×2, 经历一次池化操作, 图像块大小从28×28缩小到14×14, 得到深度为32的特征图. 将第二层卷积核设定为5×5, 数量是64, 再经过一个2×2的池化层可得到64张7×7像素的特征图. 最后是两个全连接层, 第一个全连接层的神经元个数为1024, 第二个全连接层的神经元个数为20. 即文中的字符分类数, 标签与字符的对应关系如表1所示.
| 表 1 标签字符对应关系 |
2.2 实验测试及分析
为验证CNN模型的泛化性能, 实验统计了模型对数字和新增数学符号的识别准确率. 训练集为EQU-MNIST字符训练库, 测试集来自不同年龄段多名学生的手写体数据, 包括每类字符1000张, 合计20 000张的标准化字符图像. 实验结果如图3所示.

|
图 3 基于EQU-MNIST训练集的字符分类准确率 |
观察图3柱状图的趋势可以发现, 除“1”“7”“>”“)”4类字符外, 其他字符的识别准确率都稳定在98.5%以上, 而最低的也达到97%以上, 说明本文的CNN模型对新的数据集也具有良好的适应能力. 同时, 97%以上的字符识别率也保证了本文分类模型的可应用性.
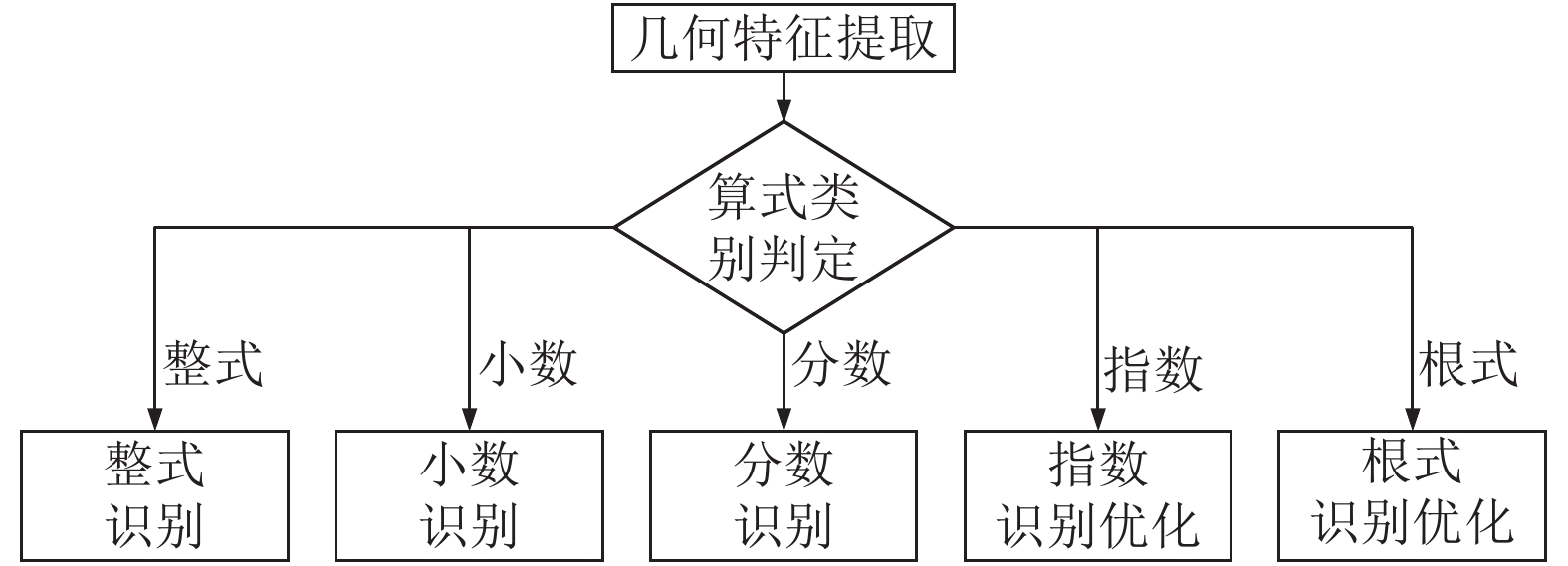
3 基于多重几何特征的手写算式识别虽然CNN分类算法在单个字符识别上已经达到97%以上的识别率, 可直接进行整式的判别, 却无法识别小数、分数、指数、根式等具有复杂二维空间结构的手写数学算式. 为此, 本文提出一种基于多重几何特征的脱机手写算式识别算法, 算法流程如图4所示: 首先, 提取待识别手写算式的几何特征; 然后, 基于不同算式所属知识点的学段, 结合多重几何特征定义结构解析规则, 判定算式类别, 实现识别模型, 并重点针对小猿口算、作业帮(家长版)未实现的初中知识点中的复杂指数和根式识别进行优化; 最后, 采用分治算法实现由以上各种算式组合嵌套的复合手写算式(见图5)识别.
|
图 4 手写算式识别算法流程图 |
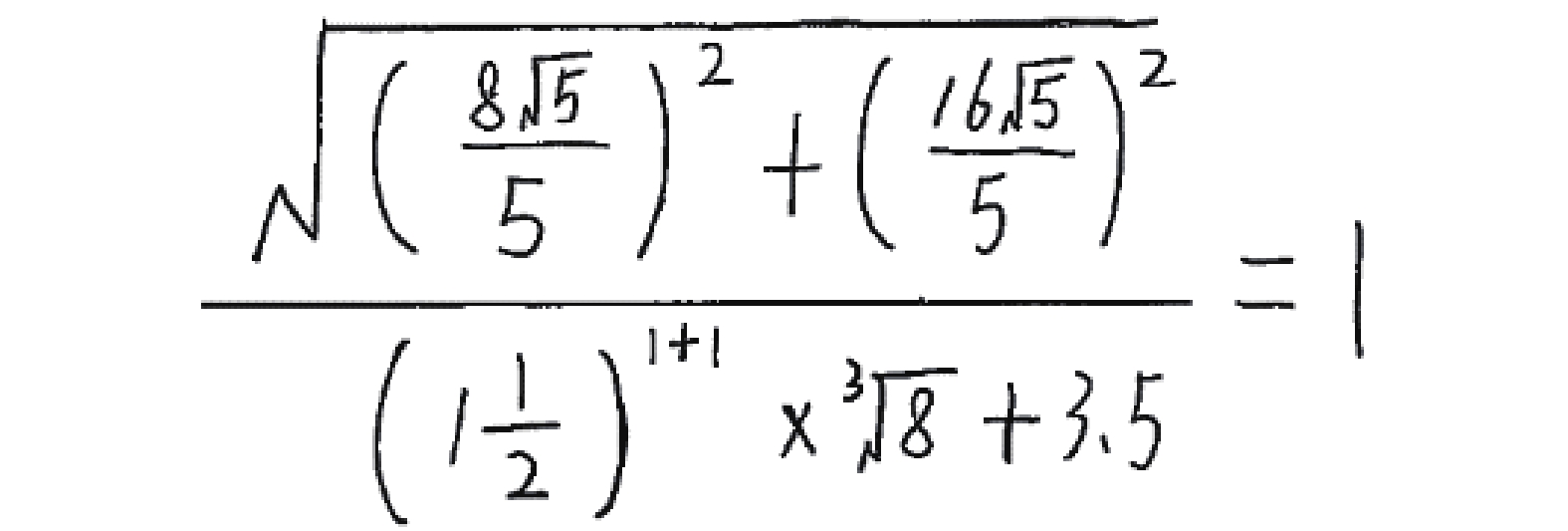
|
图 5 复合手写算式样例 |
3.1 多重几何特征提取
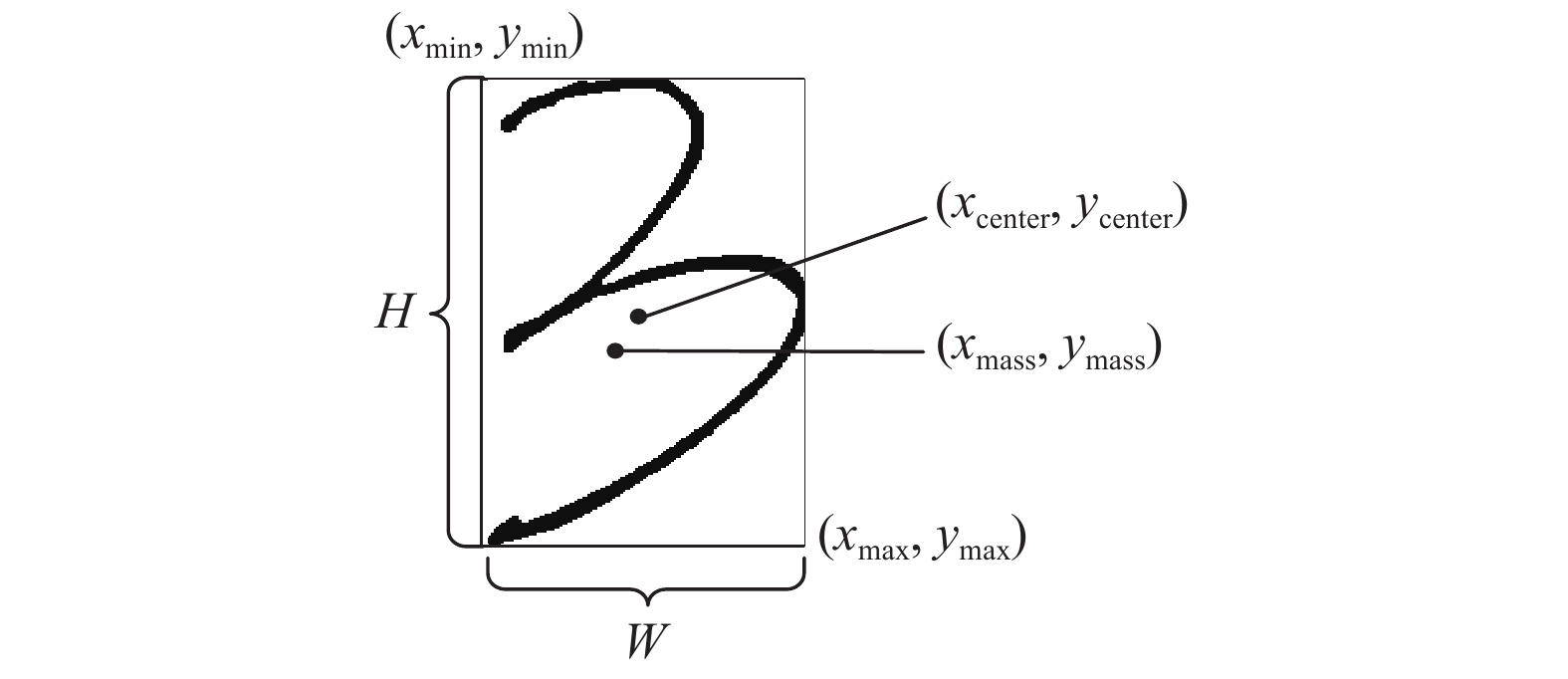
文中设定原始图像的左上角坐标为坐标原点, 坐标轴为X轴水平向右, Y轴竖直向下. 因此经图像预处理后的字符图像
|
图 6 字符几何特征 |
字符几何特征的定义如下:
定义1. 图像的质心, 也称为图像的重心. 将图像中每一点的像素值理解成此点处的质量. 图像的质心反映了目标像素值的集中位置. 假设图像
| ${M_{pq}} = \sum\limits_x {\sum\limits_y {g{\rm{(}}x,y{\rm{)}}} } \cdot {x^p} \cdot {y^q}$ | (1) |
依据
| ${{(}}{x_{\rm mass}},{y_{\rm mass}}{\rm{) = (}}{{{M_{10}}}/{{M_{00}}}},{{{M_{01}}}/{{M_{00}}}}{\rm{)}}$ | (2) |
以上定义反映的是单个字符的几何特性, 不能有效地表达相邻字符间的空间位置关系. 为进一步实现算式符号的重组识别, 本文基于单个字符的几何特征, 选取高度比
字符对几何特征的定义如下:
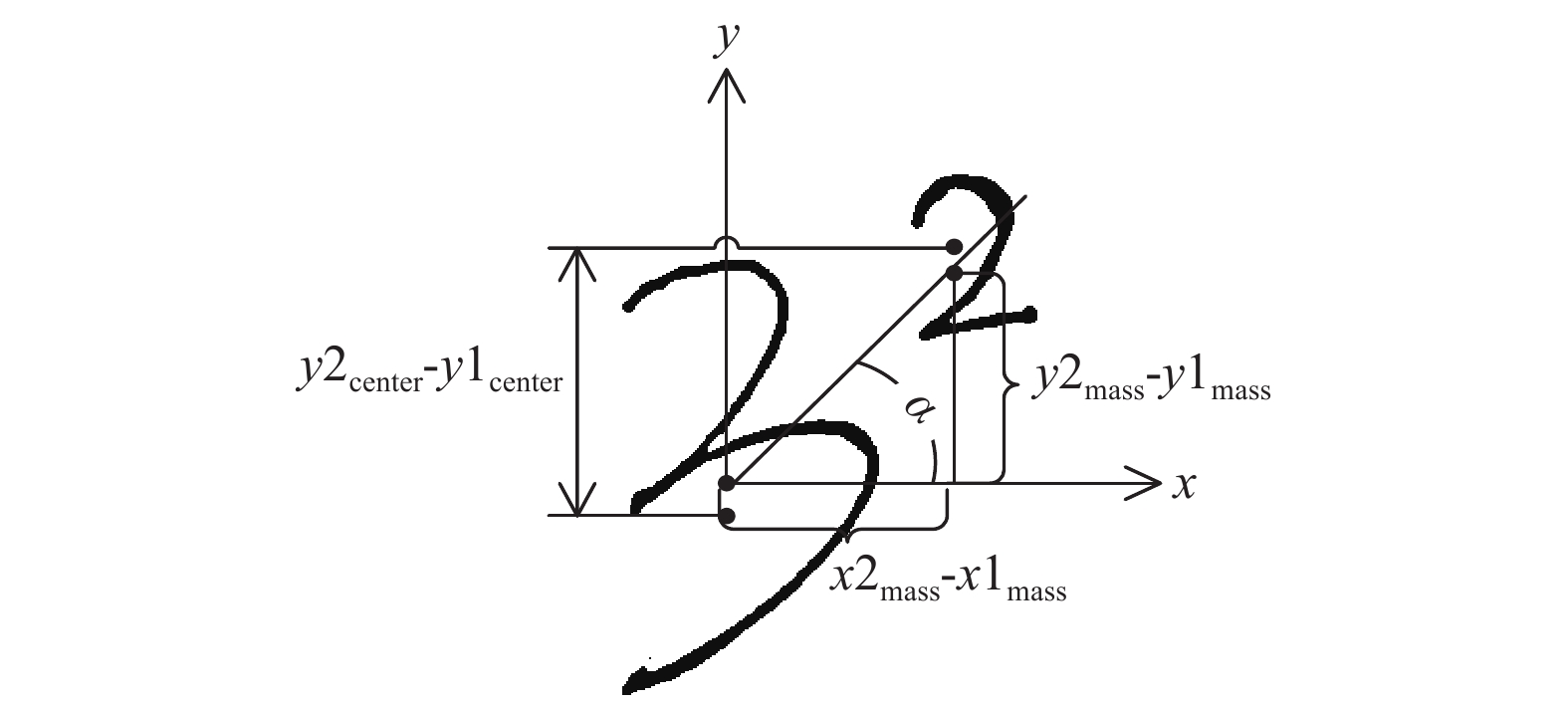
定义2. 如图7所示, 依据字符对的质心坐标定义质心偏移角度. 质心偏移角度反映了相邻字符间的相对位置关系.
| $\alpha = \arctan {\rm{(}}\dfrac{{y{2_{\rm mass}} - y{1_{\rm mass}}}}{{x{2_{\rm mass}} - x{1_{\rm mass}}}}{\rm{)}}$ | (3) |
|
图 7 字符对几何模型 |
定义3. 基于前一字符的高度值和字符对的中心坐标定义中心偏移量. 中心偏移量反映了相邻字符在竖直方向上的紧邻度.
| $\delta = \dfrac{{y{2_{\rm center}} - y{1_{\rm center}}}}{{H1}}$ | (4) |
定义4. 据字符的四元组信息定义水平重叠区间比, 垂直重叠区间比.
| $HOR = \dfrac{{len{\rm{([}}\max{\rm{(}}x{{\rm{1}}_{\min}},x{{\rm{2}}_{\min}}{\rm{)}},\min {\rm{(}}x{{\rm{1}}_{\max }},x{{\rm{2}}_{\max }}{\rm{)])}}}}{{len{\rm{([}}x{{\rm{1}}_{\min}},x{{\rm{1}}_{\max }}{\rm{])}}}}$ | (5) |
| $VOR = \dfrac{{len{\rm{([}}\max{\rm{(}}y{{\rm{1}}_{\min}},y{{\rm{2}}_{\min}}{\rm{)}},\min {\rm{(}}y{{\rm{1}}_{\max }},y{{\rm{2}}_{\max }}{\rm{)])}}}}{{len{\rm{([}}y{{\rm{1}}_{\min}},y{{\rm{1}}_{\max }}{\rm{])}}}}$ | (6) |
其中,
定义5. 于多个字符的二维坐标定义多字符中心坐标:
| $\begin{split} &{\rm{(}}{X_{\rm center}},{Y_{\rm center}}{\rm{) =}}\\ &\left(\dfrac{{\min{\rm{(}}x{{\rm{1}}_{\min}}, \cdots ,x{n_{\min}}{\rm{) + }}\max {\rm{(}}x{{\rm{1}}_{\max }}, \cdots ,x{n_{\max }}{\rm{)}}}}{{\rm{2}}},\right.\\ &\left.\dfrac{{\min{\rm{(}}y{{\rm{1}}_{\min}}, \cdots ,y{n_{\min}}{\rm{) + }}\max {\rm{(}}y{{\rm{1}}_{\max }}, \cdots ,y{n_{\max }}{\rm{)}}}}{{\rm{2}}}\right) \end{split}$ | (7) |
小数点通常位于小数运算中相邻两个字符的偏下位置, 因此本文基于字符高度, 中心坐标, 相邻字符识别结果等特征, 设定小数运算的判定规则如下:
| $\left\{\begin{split} &{\rm{(1)}}\;y{{\rm{2}}_{\min }} > y{1_{\rm center}}\;{\rm and}\;y{2_{\min }} > y{3_{\rm center}}\\ &{\rm{(2)}}\;y{2_{\min }} > {\rm{(}}y{1_{\min }}{\rm{ + }}y{3_{\min }}{\rm{)}}/2\\ &{\rm{(3)}}\;H2 < {\rm{(}}H{\rm{1}}/2{\rm{ + }}H3/2{\rm{)}}/2\\ &{\rm{(4)}}\;{\text{相邻两个字符均为数字}} \end{split}\right.$ |
如果目标字符与相邻两个字符满足上述判定规则, 则说明字符间属于小数关系, 文中设定小数点的字符标记为20, 进一步得到小数识别算法流程如图8所示.

|
图 8 小数识别算法流程图 |
分数是由分子、分号和分母组合的具有上中下位置关系的数学算式. 本文选取宽高比, 中心偏移量, 水平重叠区间比, 多字符中心坐标作为分数运算的几何特征识别指标. 在识别分数时均转换为等价的除法运算, 同时, 添加一组圆括号保证分数运算转换为除法运算时的优先级. 具体识别算法流程如图9所示.
图9中的分数识别算法只能识别真分数, 假分数等常见分数, 为使识别算法能够完全实现中小学数>学课堂中的分数判别, 本文进一步处理类似于
算法1. 分数识别算法.
输入: 原始识别列表oriList
输出: 带分数识别结果串resultStr
Step 1. 逆序遍历原始识别列表oriList, 记录带分数的整数系数在列表中的终止索引endIndex, 起始索引startIndex.
Step 2. 基于索引从原始列表oriList中提取带分数的整数系数列表, 并依据表1标签字符对应关系转换成整数字符串integerStr.
Step 3. 基于终止索引endIndex从原始列表oriList中提取带分数的真分数字符串fractionStr.
Step 4. 将带分数的整数系数字符串与真分数字符串相加, 生成结果字符串resultStr=“(”+integerStr+“+”+fractionStr+“)”.
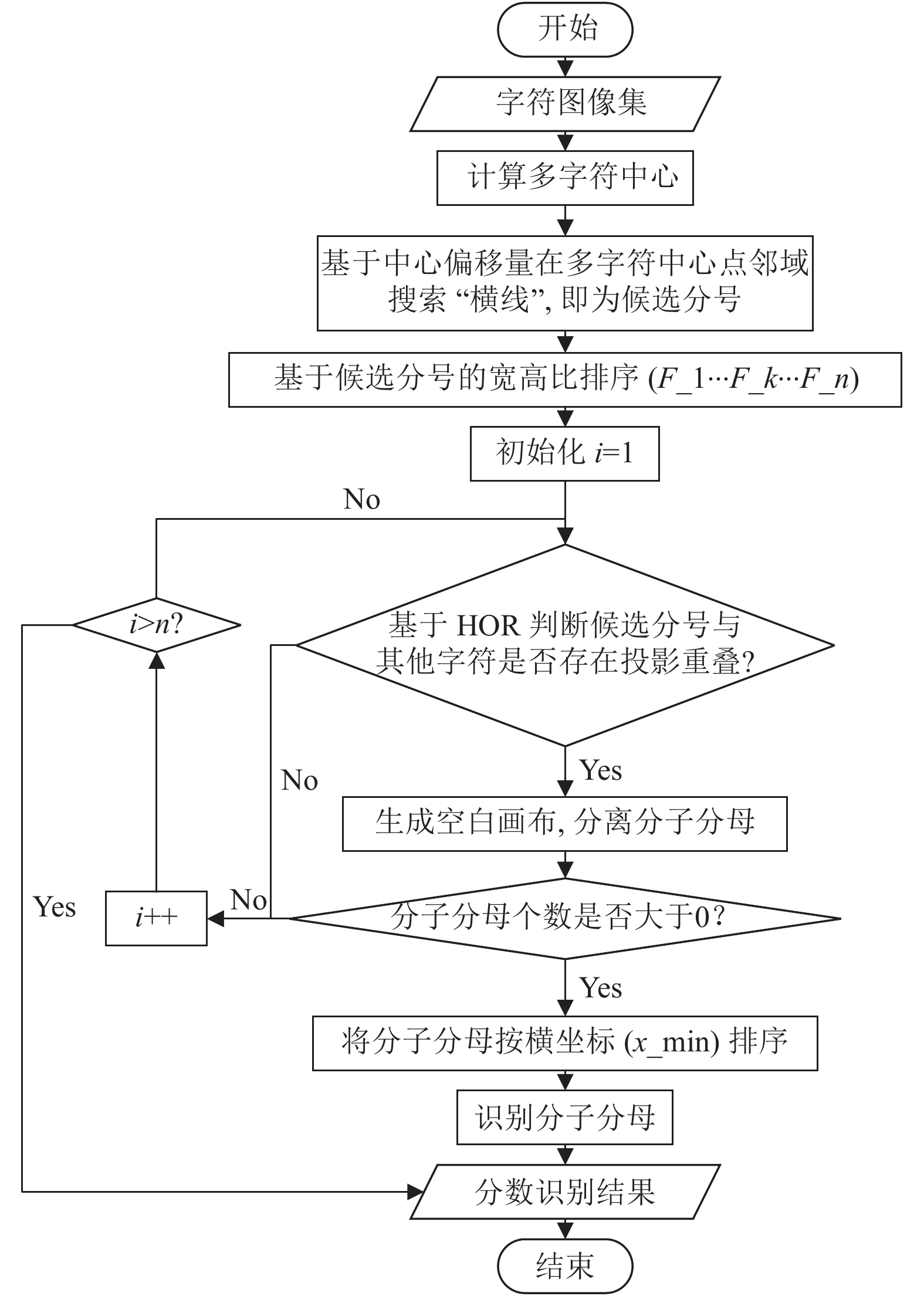
|
图 9 分数识别算法流程图 |
3.3 指数和根式识别优化
指数运算属于典型的上下结构的数学算式, 指数一定位于底数的右上角位置, 因此本文基于字符高度, 高度比, 质心偏移角度多重几何特征, 设定指数运算的判定规则:
| $\left\{\begin{split} &{\rm{(1)}}\;y{2_{\min }} < y{1_{\min }} - 1/7*H2\\ &{\rm{(2)}}\;y{2_{\min }} + H2 < y{1_{\min }} + 4/7*H1\\ &{\rm{(3)}}\;2/7 < HR < 6/7\\ &{\rm{(4)}}\;\pi /12 < \alpha < 5\pi /12 \end{split}\right.$ |
如果相邻两个字符满足上述判定规则, 则说明字符间属于指数关系, 进一步得到指数识别算法的伪代码如下:
Input: charImages, charLabels
Output: exponentialresult
baseLabel = [] # 底数字符标记
indexLabel = [] # 指数字符标记
i = 1 # 从第二个字符开始遍历
while i < len(charImages):
priorCharImage = charImages[i–1]
# 第一步: 获取指数标记列表
tempI = i
while tempI < len(charImages) and isexponent-
ial(priorCharImage, charImages[tempI]):
indexLabel.append(charLabels[tempI])
tempI = tempI + 1
# 第二步: 获取底数标记列表
if len(indexLabel) > 0:
baseLabel.append(charLabels[0: i])
if tempI != i:
i = tempI – 1
i = i + 1
# 第三步: 组合指数识别结果串
exponentialresult = ["pow(" + list2str(baseLabel) + "," + list2str(indexLabel) + ")"]
其中, 函数isexponential基于判定规则实现相邻字符指数关系的判别, 函数list2str依据表1将标记列表转换成识别字符串.
为实现对根式识别模型的优化, 首先需要完成对特殊符号根号的判别, 而根号(
算法2. 根号识别算法.
输入: 字符图像image
输出: 识别结果result(True or False)
Step 1. 基于角点提取算法获取字符的拐点信息, 并对其进行编号(如图10(a)所示), 如果拐点个数小于4, 则result=False; 否则, 执行Step2.
Step 2. 依据根号的①②③拐点信息定义半包围结构的有效区域(如图10(b)所示).
Step 3. 基于
基于算法2, 本文依据“减法”思想完成根式的识别: 首先从字符图像集中移除根号, 再进行根指数和根底数的识别, 最后完成根式字符串的构建, 具体算法实现如下:
算法3. 根式识别算法.
输入: 字符图像集images
输出: 根式识别结果串radicalStr
Step 1. 遍历字符图像集images, 基于算法2判断是否存在根号, 如果存在, 则执行Step2; 否则, 返回根式识别结果串radicalStr.
Step 2. 基于根号的②③拐点信息提取根指数图像, 识别分类并转换为根指数字符串indexStr.
Step 3. 基于根式转指数的运算规则, 若indexStr为空, 则indexStr=“1/2”; 否则, indexStr=“1/”+indexStr.
Step 4. 依据根号的半包围结构的有效区域, 结合
Step 5. 构建根式识别字符串radicalStr=“pow(”+baseStr+“,”+indexStr+“)”.
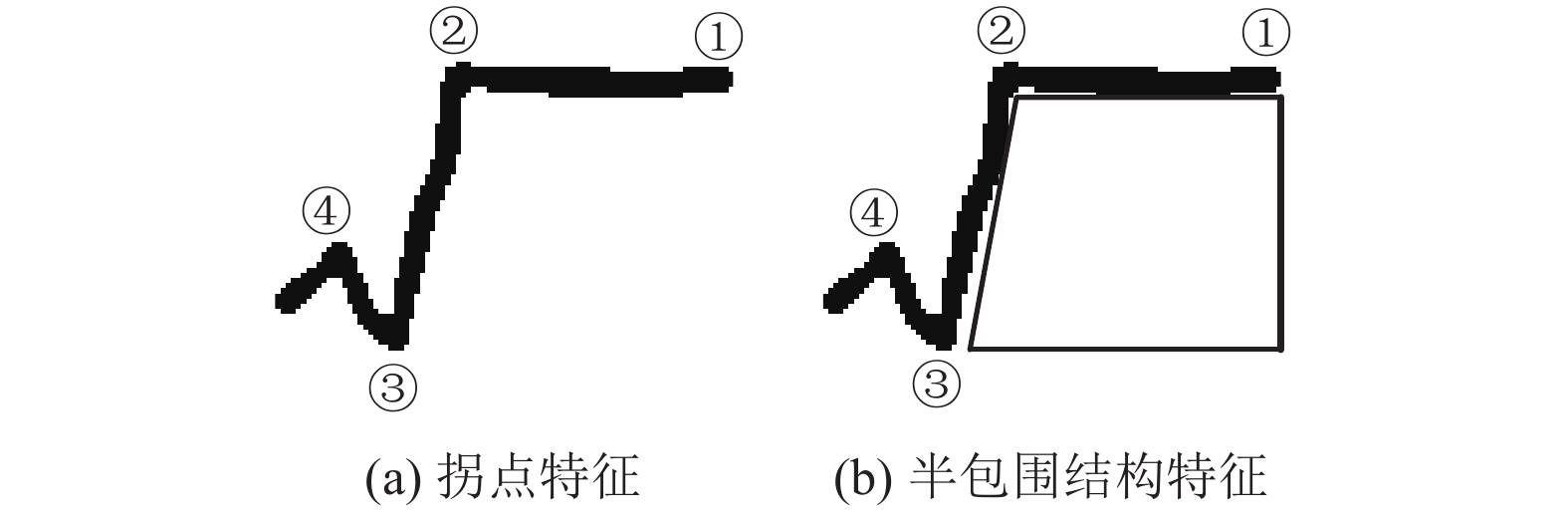
|
图 10 根号的结构特征 |
算法3只能识别
算法4. 带系数的根式识别算法.
输入: 原始识别列表oriList
输出: 带系数的根式识别结果串resultStr
Step 1. 逆序遍历原始列表oriList, 记录系数在列表中的终止索引endIndex, 起始索引startIndex.
Step 2. 基于索引从原始列表oriList中提取系数列表, 并依据表1标签字符对应关系转换成系数字符串coefficientStr.
Step 3. 基于终止索引endIndex从原始列表oriList中提取原有根式字符串oriRadicalStr.
Step 4. 解析原有根式字符串oriRadicalStr, 提取根底数base, 根指数exponent.
Step 5. 将系数字符串coefficientStr转换成与oriRadicalStr根指数相同的同次根式字符串coeRadicalStr.
Step 6. 依据同次根式的乘法规则(根指数不变, 根底数相乘), 合并oriRadicalStr与coeRadicalStr, 生成结果字符串resultStr.
3.4 复合算式识别数学算式具有二维空间结构, 在水平分布的基础上, 分数、指数、根式还具有其内嵌结构, 这种特征使得复合算式识别过程适合用数据结构中的树来表示. 如图11所示, 本文采用分治算法实现复合数学算式的识别, 具体识别过程如图11所示.

|
图 11 复合算式识别 |
图11描述了手写复合算式的识别过程: 首先, 基于分治算法, 结合已实现的手写算式识别算法(见图4)将复合算式逐层分解, 直至所有的简单算式(如小数, 分数, 指数以及根式)和单个字符都位于树的最底层, 作为树的叶子节点. 然后, 基于运算规则将这些简单算式和字符向上合并, 直到生成树的根结点为止, 即手写复合算式被识别出来. 以树的第二层第一个节点(从左往右)为例, 依据手写算式识别算法将该算式判定为分数; 接着提取分子笔划部分, 并将这部分笔划序列按照字符切分、手写算式识别的处理方式递归进行, 直到所有节点均不可再拆分为止, 然后逐层将子节点的识别结果串组合生成父节点的识别序列, 最终得到分子的识别结果串, 同理, 得到分母的识别结果串; 再将分子, 分号, 分母三者的识别结果串组合作为一个新的识别序列添加到根节点的子识别序列中.
4 实验测试与分析 4.1 实验环境及数据基于以上研究, 设计并实现基于多重几何特征和CNN的脱机手写算式识别系统. 系统环境参数信息如表2所示.
| 表 2 系统环境参数信息 |
实验测试数据来自不同年龄段32名学生(小学生10名, 初中生10名, 大学生12名)的76幅手写体数学算式图像, 合计2660个手写算式, 算式类别及数量分布如表3所示.
| 表 3 算式类别及数量 |
4.2 实验结果及分析
为验证识别算法的有效性, 本文采用算式识别准确率作为评价标准, 数学定义如下:
| $p = \frac{{TN}}{{TN + FN}} \times 100\% $ | (8) |
其中,
本文设定图像分辨率、光照、噪声等图像特征参数作为影响实验结果的自变量. 采用控制变量法验证不同特征参数对算式识别率的影响, 参数取值及对应的实验结果如表4所示.
| 表 4 参数取值及对应的实验结果 |
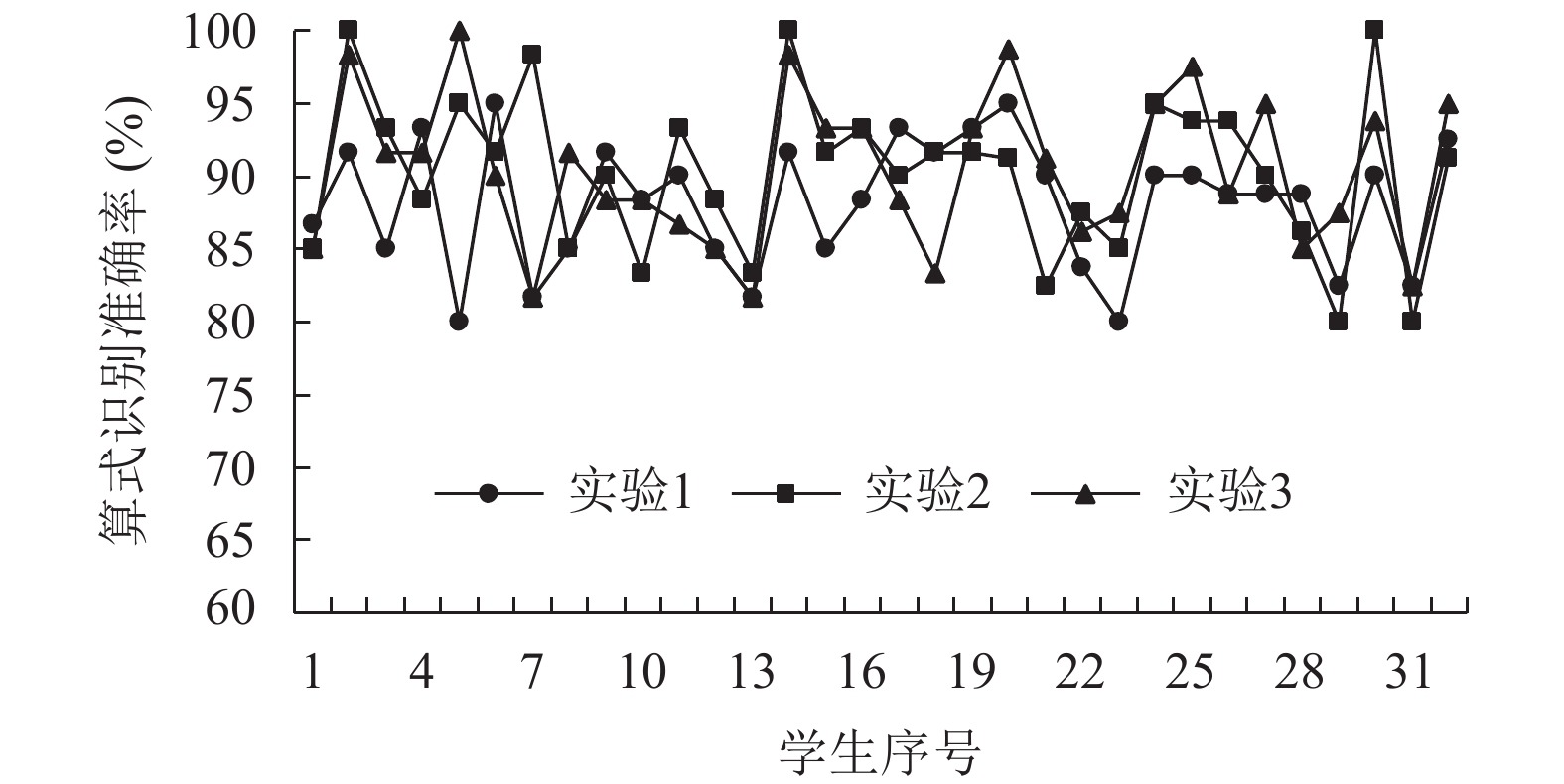
|
图 12 图像分辨率对算式识别率的影响 |

|
图 13 光照对算式识别率的影响 |
|
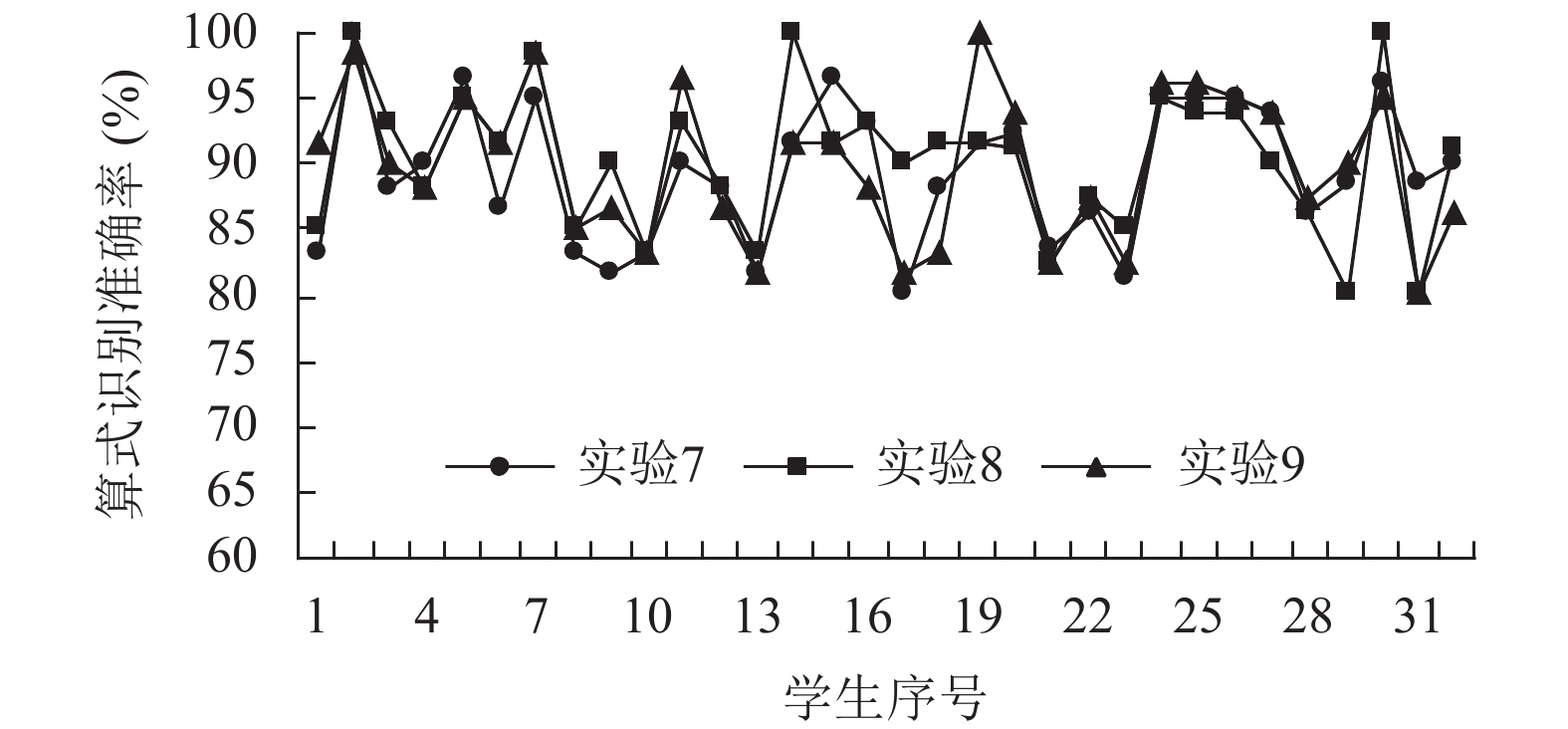
图 14 噪声对算式识别率的影响 |
观察图12~图14中折线图的走势, 每组实验的折线图并未完全重合, 说明图像分辨率、光照、噪声等图像特征参数对实验结果有一定的影响, 但仍在合理范围内. 同时, 本文系统在九组实验中的算式识别准确率基本稳定在80%以上, 算式平均识别率也维持在88.15%~90.43%之间, 验证了该系统在不同条件下均具有较好的稳定性, 可靠性和实用性.
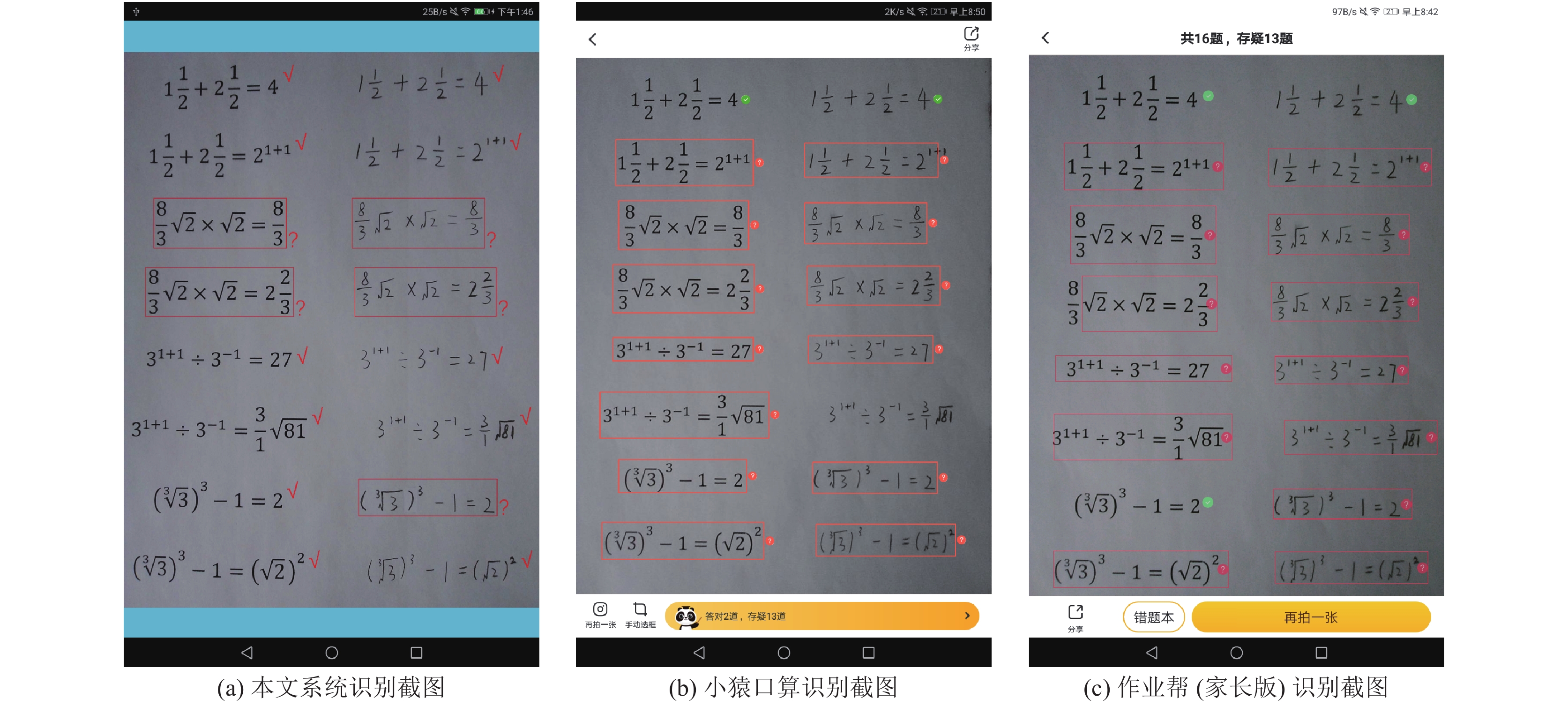
为验证手写算式识别算法对复杂指数和根式识别的优化效果, 进一步评价系统的性能, 将本文系统与目前市场上主流的小猿口算、作业帮(家长版)进行对比实验, 比较不同系统的算式识别准确率, 测试集采用本文的实验测试数据. 系统识别效果截图见图15, 实验结果如表5所示.
由图15可知, 本文的手写算式识别算法实现了对初中知识点中复杂指数和根式识别的优化. 同时, 分析表5可知, 本文系统的算式识别率最高, 相比其他系统的优势十分明显, 进一步验证了本文系统的实用性.
|
图 15 3个系统识别效果截图 |
| 表 5 不同系统算式识别率对比 |
5 结论与展望
脱机手写算式识别一直是智慧教育领域研究的热点与难点, 本文重点针对中小学数学课堂中的手写算式, 提出了一种基于多重几何特征和CNN的脱机手写算式识别的解决方案, 有效地提高了手写算式识别的准确率, 并以此为基础设计实现了脱机手写算式识别系统, 解决了数学算式智能计算的问题, 实现了手写算式的自动评阅, 将应用于陕西省数所中小学的课堂教学中. 依托该系统可以高效便捷地完成学生作业的批阅, 减轻教师负担, 减少重复劳动和主观误判, 显著提高课堂效率, 具有很强的实际意义.
| [1] |
张松林, 李雪. 灵敏度正则化极限学习机及其在数字识别中的应用. 计算机系统应用, 2017, 26(6): 143-147. DOI:10.15888/j.cnki.csa.005823 |
| [2] |
Mellouli D, Hamdani TM, Sanchez-Medina JJ, et al. Morphological convolutional neural network architecture for digit recognition. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(9): 2876-2885. DOI:10.1109/TNNLS.2018.2890334 |
| [3] |
Wang F, Zhu HQ, Li W, et al. A hybrid convolution network for serial number recognition on banknotes. Information Sciences, 2020, 512: 952-963. DOI:10.1016/j.ins.2019.09.070 |
| [4] |
王维, 万文略. 基于组合特征的手写英文字母识别方法. 计算机应用, 2018, 38(S2): 286-289. |
| [5] |
叶锋, 邓衍晨, 汪敏, 等. 部分级联特征的离线手写体汉字识别方法. 计算机系统应用, 2017, 26(8): 134-140. DOI:10.15888/j.cnki.csa.005913 |
| [6] |
Wang QF, Yin F, Liu CL. Unsupervised language model adaptation for handwritten Chinese text recognition. Pattern recognition, 2014, 47(3): 1202-1216. DOI:10.1016/j.patcog.2013.09.015 |
| [7] |
Alvaro F, S’nchez JA, Benedi JM. Recognition of printed mathematical expressions using two-dimensional stochastic context-free grammars. Proceedings of 2011 International Conference on Document Analysis and Recognition. Beijing, China. 2011. 1225–1229.
|
| [8] |
宗亚辉, 李双庆. 印刷体数学公式的结构分析与识别. 计算机工程与应用, 2015, 51(9): 196-200. DOI:10.3778/j.issn.1002-8331.1305-0486 |
| [9] |
Aly W, Uchida S, Suzuki M. Automatic classification of spatial relationships among mathematical symbols using geometric features. IEICE Transactions on Information and Systems, 2009, E92–D(11): 2235-2243. DOI:10.1587/transinf.E92.D.2235 |
| [10] |
Wang JM, Du J, Zhang JS, et al. Multi-modal attention network for handwritten mathematical expression recognition. Proceedings of 2019 International Conference on Document Analysis and Recognition. Sydney, Australia. 2019. 1181–1186.
|
| [11] |
Dai JY, Sun Y, Su GP, et al. Recognizing offline handwritten mathematical expressions efficiently. Proceedings of the 10th International Conference on E-Education, E-Business, E-Management and E-Learning. Tokyo, Japan. 2019. 198–204.
|
| [12] |
胡龙灿, 杨帆, 樊爱军. 手写数学公式的识别研究及在Android上的应用. 计算机应用与软件, 2014, 31(8): 28-31, 44. DOI:10.3969/j.issn.1000-386x.2014.08.008 |
| [13] |
卢蓉, 范勇, 陈念年, 等. 一种提取目标图像最小外接矩形的快速算法. 计算机工程, 2010, 36(21): 178-180. DOI:10.3969/j.issn.1000-3428.2010.21.064 |
| [14] |
杨谢柳, 牛玺辉, 梁文峰. 面向非规则排列汉字文本的字符分割方法. 计算机辅助设计与图形学学报, 2019, 31(9): 1542-1548. DOI:10.3724/SP.J.1089.2019.17608 |
| [15] |
Liu CL, Nakashima K, Sako H, et al. Handwritten digit recognition: Investigation of normalization and feature extraction techniques. Pattern Recognition, 2004, 37(2): 265-279. DOI:10.1016/s0031-3203(03)00224-3 |
| [16] |
王改, 郑启龙, 邓文齐, 等. 基于BWDSP众核的CNN计算任务划分优化. 计算机系统应用, 2019, 28(9): 88-94. DOI:10.15888/j.cnki.csa.007055 |
 2020, Vol. 29
2020, Vol. 29


