1979年, Shamir[1] 和Blakley[2]分别独立提出了秘密分享(Secret Sharing, SS)概念并基于不同数学工具构造了相应方案. 秘密分享一般包含一个发送者和多个参与者, 在秘密分发阶段发送者将秘密值分成多个子秘密, 并将每个子秘密安全地发送给对应的参与者. 在重构阶段满足条件的参与者集合中的参与者合作重构出秘密值, 不满足条件的参与者集合中的参与者则不能得到关于秘密值的任何信息. 作为重要的密码技术, 秘密分享自提出以来一直受到研究者的持续关注.
函数秘密分享方案(Function Secret Sharing, FSS)与传统的秘密分享方案[1,2]最主要的不同在于它分享的秘密为函数而不是具体数值. 一个
$n$
方的FSS方案可以简单地描述如下, 在分发阶段发送者将秘密函数
$f: $
${D_f} \to {R_f}$
, 其中
${D_f},{R_f}$
分别表示秘密函数的定义域和值域, 可加地分为
$n$
个子函数
${f_1},\cdots ,{f_n}$
, 并将子函数安全地发送给相应的参与者. 其正确性要求秘密函数可以通过计算
$f = \displaystyle\sum\limits_{i = 1}^n {{f_i}} $
被正确地重构, 安全性要求子函数集合
${\rm{\{ }}{f_1}, \cdots ,{f_n}{\rm{\} }}$
的任何真子集完全掩盖了秘密函数的全部信息. 在FSS方案中, 子函数的长度与该FSS方案的通信复杂度直接相关, FSS方案的通信复杂度为所有需要传输的子函数的长度之和. FSS在提高多服务器环境下的私密信息存取的效率, 如: 私密信息恢复[3], 私密信息存储[4]等方面有着重要的应用.
针对于点函数
${f_{a,b}}(x):{\{ 0,1\} ^l} \to {{\rm{\{ 0,1\} }}^m}$
, 其中
${\{ 0,1\} ^l}, $
${\{ 0,1\} ^m}$
分别表示点函数的定义域和值域, 任意的
${x_0} \in $
${\{ 0,1\} ^n}$
, 若
${x_0} = a$
有
${f_{a,b}}({x_0}) = b$
, 否则有
${f_{a,b}}({x_0}) = 0$
. Gilboa等[5]基于伪随机生成器构造了子函数长度为
${\rm O}(\lambda {l^{\log _2^3}})$
的两方FSS方案, 其中
$\lambda $
为伪随机生成器的种子长度, 并将构造的两方FSS方案应用到了提高两服务器的私密信息检索协议的效率中, 得到了通信复杂度为
${\rm O} $
$(\lambda {l^{\log _2^3}})$
的两方私密信息检索协议. 之后Boyle等[6]利用二叉树技术降低了文献[5]中两方FSS方案的通信复杂度, 构造了子函数长度为
${\rm O}(\lambda l)$
的两方FSS方案. 此外Boyle等[6]构造了通信复杂度为
${\rm O}(\lambda {2^{l + n - 1/2}})$
的
$n(n \ge 3)$
方的FSS方案. 在此基础上Boyle等[6]提出了函数秘密分享概念并对其进行了系统的介绍, 指出FSS与密码学中的其他概念, 例如: 同态秘密分享(Homomorphic Secret Sharing, HSS)[7], 完全同态加密(Fully Homomorphic Encryption, FHE)[8]等其他密码学概念之间存在着密切的联系. 在文献[9]中Boyle等使用代数中的张量操作简化了文献[6]中的两方的FSS方案的构造并将其通信复杂度降低了4倍.
文献[5,6,9]中的FSS方案在重构阶段要求所有的参与者均参与重构. 而在实际生活中往往存在参与者因为自身原因不能参与重构的场景, 例如某个参与者在方案运行的过程中掉线, 因此导致整个FSS方案无法正常运行. 除此之外他们的FSS方案都是基于伪随机生成器构造的, 因此其安全性基于密码学中单向函数存在性假设[10], 这说明了他们的FSS方案均为计算意义下安全的FSS方案, 即只可以抵抗计算能力有限的敌手.
为了使FSS方案可以更加灵活地应用于现实场景, 以及具有更高级别的安全性, 本文采用多项式技术构造了信息论意义下安全的门限函数秘密分享(Threshold Function Secret Sharing, TFSS)方案, 在重构过程中可以容忍部分参与者不参与重构, 因此可以更加灵活地应用到实际场景中. 对构造的方案按照FSS方案所定义的t-安全性(即任意t个参与者联合不能得到秘密函数任何信息)进行严格的安全性证明, 证明结果表明本文构造的TFSS方案满足信息论意义下的t-安全性, 即可以抵抗具有无限计算能力的敌手, 因此相对于文献[5,6,9]中的FSS方案本文构造的TFSS方案具有更高级别的安全性. 除此之外当分享的秘密函数为点函数
${f_{a,b}}(x):{\{ 0,1\} ^l} \to {{\rm{\{ 0,1\} }}^m}$
时, 本文构造的TFSS方案的通信复杂度为
${\rm O}(l)$
. 低于文献[5,6,9]中FSS方案的通信复杂度. 另外我们注意到Yuan等[11]运用多项式插值技术构造了含有门限的FSS方案, 但是Yuan等并没有对其方案按照FSS方案所定义的t-安全性进行严格的安全性证明. 经过分析发现, 在他们的方案中任意一个参与者可以通过自己收到的子函数得到秘密函数的部分信息, 进而任意两个参与者联合就可以得到整个秘密函数, 因此其方案不能满足t-安全性. 本文对他们构造不满足t-安全性的原因进行了具体分析和阐述.
1 相关概念
本节将给出本文所用到的一些概念和定义, 包括点函数的定义, Shamir门限秘密分享方案, 函数秘密分享方案的定义及其安全模型.
定义1(点函数). 设
${{\rm{\{ 0, 1\} }}^l}$
为定义域,
${{\rm{\{ 0, 1\} }}^m}$
为值域, 其中
$l,m$
为正整数, 则对任意的
$a \in {\{ 0,1\} ^l}$
,
$b \in {\{ 0,1\} ^m}$
, 点函数
${f_{a,b}}(x):{{\rm{\{ 0,1\} }}^l} \to {\{ 0,1\} ^m}$
的定义如下: 对任意的
$x \in $
$ {{\rm{\{ 0,1\} }}^l}$
有,
${f_{a,b}}(x) = \left\{ {\begin{array}{*{20}{c}} {0,x \ne a} \\ {b,x = a} \end{array}} \right.$
.
定义2 (Shamir门限秘密分享方案[1]). 令
$G{F_q}$
为q元有限域, D为发送者,
$P = \{ {P_1}, \cdots ,{P_n}\} $
为n个参与者组成的集合且
$q > n$
,
${{\textit{z}}_1}, \cdots ,{{\textit{z}}_n}$
为
$G{F_q}$
上n个两两不同的非零公开值. 若
$s \in G{F_q}$
为秘密值, r为门限值, 则
$(r,n)$
-Shamir 门限秘密分享方案包含以下两个阶段:
1)分发阶段: 发送者D从有限域
$G{F_q}$
中随机均匀地选取
$r - 1$
个值
${a_1}, \cdots ,{a_{r - 1}}$
, 生成
$r - 1$
次多项式
$f(x) = s + $
$ {a_1}x + \cdots + {a_{r - 1}}{x^{r - 1}}$
, 发送者D计算
${s_i} = f({{\textit{z}}_i}) $
$(i = 1, \cdots ,n)$
, 并将
${s_i}$
安全地发送给每位参与者
${P_i}$
.
2)重构阶段: 对任意r个参与者
$\{ {P_{{i_1}}}, \cdots ,{P_{{i_r}}}\} \subseteq \{ {P_1}, \cdots ,$
${P_n}\} $
, 他们利用公开值
${{\textit{z}}_1}, \cdots ,{{\textit{z}}_n}$
计算值插值系数
${c_{{i_h}}} = $
$\displaystyle\prod\limits_{h' = 1,h' \ne h}^r {\dfrac{{ - {{\textit{z}}_{{i_{h'}}}}}}{{{{\textit{z}}_{{i_h}}} - {{\textit{z}}_{{i_{h'}}}}}}} $
, 并通过多项式插值公式重构出秘密
$s = \displaystyle\sum\limits_{h = 1}^r {{c_{{i_h}}}} \cdot {s_{{i_h}}}$
.
定义3 (函数秘密分享[5]). 设1λ为安全参数,
${D_f}$
为定义域,
${R_f}$
为值域, 秘密函数为
$f(x):{D_f} \to {R_f}$
, n为参与者个数, r为重构门限值, 则t-安全
$(t < r < n)$
的FSS方案定义为以下3个算法
$(Gen,Eval,Dec)$
, 其中
$Gen$
为子函数生成算法,
$Eval$
为子函数计算算法,
$Dec$
为输出解码器, 具体如下:
(1)
$Gen({1^\lambda },f) \to ({k_1}, \cdots ,{k_n})$
: 输入安全参数和秘密函数, 输出n个子函数
${k_1}, \cdots ,{k_n}$
.
(2)
$Eval(i,{k_i},{x_0}) \to {y_i}$
: 任意的
${x_0} \in {D_f}$
, 参与者
${P_i}(i = $
$ 1, \cdots ,n)$
输入
$(i,{k_i},{x_0})$
, 输出值
${y_i}$
.
(3)
$Dec({y_{{i_1}}}, \cdots ,{y_{{i_r}}}) \to f({x_0})$
: 输入
$({y_{{i_1}}}, \cdots ,{y_{{i_r}}})$
, 输出秘密函数在点
${x_0}$
处的函数值
$f({x_0})$
.
上述方案满足以下正确性和t-安全性:
正确性: 若上述FSS方案中的3个算法(Gen, Eval, Dec)都能顺利且正确的执行, 则任意r个参与者可以重构出秘密函数
$f(x):{D_f} \to {R_f}$
在
${x_0}$
处的函数值
$f({x_0})$
.
t-安全: 若存在受贿参与者集合
$T \subseteq \{ {P_1}, \cdots ,{P_n}\} $
且
$|T| = t$
, 则不可区分性实验
$\prod $
可描述如下:
1)敌手
${\cal{A}}$
输入安全参数1λ输出(f0,f1), 满足
${D_{{f_0}}} = {D_{{f_1}}}$
, 并将产生的(f0,f1)发送给挑战者
${\cal{C}}$
.
2) 挑战者
${\cal{C}}$
收到(f0,f1)后, 随机地选取挑战值
$c \in \{ 0,1\} $
, 执行子函数生成算法输入
${f_c}$
, 输出
$(k_1^c, \cdots ,k_n^c)$
, 并将
${{\rm{\{ }}k_i^c{\rm{\} }}_{i \in T}}$
发送给
${\cal{A}}$
.
3) 敌手
${\cal{A}}$
收到
${{\rm{\{ }}k_i^c{\rm{\} }}_{i \in T}}$
后根据自己所掌握的信息给出关于挑战值
$c$
的猜测
$\hat c$
.
用
$Adv({1^\lambda },A,T) = Pr [\hat c = c] - \dfrac{1}{2}$
表示敌手
${\cal{A}}$
在上述实验
$\prod $
中猜对挑战值
$c$
的概率与
${\cal{A}}$
在不知道任何信息下随机猜测猜对c的概率的之差.
对于任意概率多项式时间敌手
${\cal{A}}$
, 若存在关于
$\lambda $
的可忽略函数
$u(\lambda )$
[12]使得
$Adv({1^\lambda },A,T) = Pr [\hat c = c] - \dfrac{1}{2} \le$
$ u(\lambda )$
, 则我们称
$(Gen,Eval,Dec)$
为计算意义下t-安全的FSS方案.
对任意拥有无限计算能力的敌手
${\cal{A}}$
, 若
$Adv({1^\lambda }, $
$A,T) = Pr [\hat c = c] - \dfrac{1}{2} = 0$
, 则我们称
$(Gen,Eval,Dec)$
为信息论意义下
$t$
-安全的FSS方案.
通信复杂度: 用
$\Psi $
表示一个FSS方案的通信复杂度,
$\Psi = \displaystyle\sum\limits_{i = 1}^n {|{k_i}|} + \displaystyle\sum\limits_{h = 1}^r {|{y_{{i_h}}}|} $
, 其中
${\rm{|}}{k_i}{\rm{|,|}}y{}_{{i_h}}{\rm{|}}$
分别表示
${k_i},{y_{{i_h}}}$
转化为二进制比特串的长度.
2 门限FSS方案TFSS(Gen, Eval, Dec)
本节采用了多项式技术构造了TFSS方案, 按照FSS定义的t-安全的安全模型证明了本文构造的TFSS方案具有信息论意义下的t-安全性, 并对方案的通信复杂度进行了具体的分析.
2.1 TFSS(Gen, Eval, Dec)
若秘密函数为点函数
${f_{a,b}}(x):{\{ 0,1\} ^l} \to {F_q}$
, n为参与者个数,
$r = 2lt + 1$
$(r < n)$
为重构门限值, 则门限函数秘密分享方案TFSS
$(Gen,Eval,Dec)$
具体如下:
(1)
$Gen({1^\lambda },{f_{a,b}}) \to ({k_1}, \cdots ,{k_n})$
① 将
$a \in {\{ 0,1\} ^l}$
转换为二进制进行表示, 则a =
$({a_1}, \cdots ,{a_l})$
, 其中
${a_j} \in \{ 0,1\} (j = 1, \cdots ,l)$
.
② 令
$b = \displaystyle\prod\limits_{j = 1}^l {{b_j}} $
, 其中
${b_j} \in G{F_q}$
.
③ 发送者D从
$G{F_q}$
中随机均匀的选取
$lt$
个值
${r_{j,1}}, \cdots ,{r_{j,t}}(j = 1, \cdots ,l)$
, 并产生
$2l$
个关于z的
$2t$
次多项式
$\left\{ {\begin{array}{*{20}{l}}{{g_j}({\textit{z}}) = ({a_j} + {r_{j,1}} \cdot {\textit{z}} + \cdots + {r_{j,t}} \cdot {{\textit{z}}^t}) \cdot ({b_j} + {r_{j,1}} \cdot {\textit{z}} + \cdots + {r_{j,t}} \cdot {{\textit{z}}^t})}\\{{{\hat g}_j}({\textit{z}}) = (1 - ({a_j} + {r_{j,1}} \cdot {\textit{z}} + \cdots + {r_{j,t}} \cdot {{\textit{z}}^t})) \cdot ({b_j} + {r_{j,1}} \cdot {\textit{z}} + \cdots + {r_{j,t}} \cdot {{\textit{z}}^t})}\end{array}} \right.$
.
④D使用公开值
${{\textit{z}}_1}, \cdots ,{{\textit{z}}_n}$
计算
${g_{j,i}} = {g_j}({{\textit{z}}_i}),{\hat g_{j,i}} = {\hat g_j}({{\textit{z}}_i})$
, 并生成
${k_i} = ({g_{1,i}}, \cdots ,{g_{l,i}};{\hat g_{1,i}}, \cdots ,{\hat g_{l,i}})$
.
⑤ 输出
$({k_1}, \cdots ,{k_n})$
.
(2)
$Eval(i,{k_i},{x_0}) \to {y_i}$
① 对于任意的
${x_0} \in {\{ 0,1\} ^l}$
, 将
${x_0}$
用二进制表示为
${x_0} = (x_1^0, \cdots ,x_l^0)$
.
②
${P_i}$
计算
${y_i} = \displaystyle\prod\limits_{j = 1}^l {(x_j^0 \cdot {g_{j,i}} + (1 - x_j^0)(1 - {{\hat g}_{j,i}}))} $
.
③ 输出
${y_i}$
.
(3)
$Dec({y_{{i_1}}}, \cdots ,{y_{{i_r}}}) \to y$
① 参与者
${P_{{i_h}}}(h = 1, \cdots ,r)$
通过公开值
${{\textit{z}}_1}, \cdots ,{{\textit{z}}_n}$
计算
${c_{{i_h}}} = \displaystyle\prod\limits_{h' = 1,h' \ne r}^r {\frac{{ - {{\textit{z}}_{{i_{h'}}}}}}{{{{\textit{z}}_{{i_h}}} - {{\textit{z}}_{{i_{h'}}}}}}} $
.
② 输出
$y = \displaystyle\sum\nolimits_{h = 1}^r {{c_{{i_h}}} \cdot {y_{{i_h}}}}$
.
正确性: 在TFSS方案中子函数
${k_i} = ({g_{1,i}}, \cdots ,{g_{l,i}}; $
${\hat g_{1,i}}, \cdots ,{\hat g_{l,i}})(i = 1, \cdots ,n)$
, 其中,
|
$ \left\{ {\begin{array}{*{20}{l}} \!\!\!\!{{g_j}({\textit{z}}) \!=\! ({a_j}\! +\! {r_{j,1}} \!\cdot \!{\textit{z}} \!+\! \cdots \!+ {r_{j,t}} \!\cdot\! {{\textit{z}}^t}) \!\cdot\! ({b_j} + {r_{j,1}} \cdot {\textit{z}} + \cdots + {r_{j,t}} \cdot {{\textit{z}}^t})}\\ \!\!\!\!{{{\hat g}_j}({\textit{z}}) \!\!=\!\! (1 \!-\! ({a_j} \!+\! {r_{j,1}}\! \cdot\! {\textit{z}} \!+\! \cdots \!\!+\! {r_{j,t}}\! \cdot\! {{\textit{z}}^t})) \!\cdot\! ({b_j} \!+\! {r_{j,1}} \cdot {\textit{z}} \!+\! \cdots \!+\! {r_{j,t}} \!\cdot\! {{\textit{z}}^t})} \end{array}} \right.\!\!\! $
|
为关于z的2t次多项式, 且
$\left\{ {\begin{array}{*{20}{l}} {{g_j}(0) = {a_j} \cdot {b_j}} \\ {{{\hat g}_j}(0) = (1 - {a_j}) \cdot {b_j}} \end{array}} \right.$
. 在子函数计算算法中每个参与者
${P_i}(i = 1, \cdots ,n)$
计算
${y_i} = Eval(i, $
${k_i},{x_0}) = \displaystyle\prod\limits_{j = 1}^l {(x_j^0 \cdot {g_{j,i}} + (1 - x_j^0)(1 - {{\hat g}_{j,i}}))} .$
因为
$({{\textit{z}}_i},{y_i})$
为关于z的2lt次多项式
$f(z) = \displaystyle\prod\limits_{j = 1}^l {(x_j^0 \cdot {g_j}({\textit{z}}) + (1 - x_j^0)(1 - {{\hat g}_j}(z)))} $
上的一点, 所以任意
$r = 2lt + 1$
个参与者
${P_{{i_h}}}(h = 1, \cdots ,r)$
可通过子函数
${k_{{i_h}}}$
和公开值
${{\textit{z}}_1}, \cdots ,{{\textit{z}}_n}$
计算得到的
${\rm{(}}{{\textit{z}}_{{i_1}}}, $
${y_{{i_1}}}), \cdots ,{\rm{(}}{{\textit{z}}_{{i_r}}},{y_{{i_r}}})$
为多项式
$f(z)$
上的
$2lt + 1$
个点. 此时参与者
${\rm{\{ }}{P_{{i_1}}}{\rm{,}} \cdots {\rm{,}}{P_{{i_r}}}{\rm{\} }}$
可以通过多项式插值公式计算:
|
$ \begin{array}{l} y = f(0) = \displaystyle\sum\limits_{h = 1}^r {{c_{{i_h}}}} \cdot {y_{{i_h}}} = \displaystyle\prod\limits_{j = 1}^l {x_j^0 \cdot {g_j}(0) + (1 - x_j^0) \cdot {{\hat g}_j}(0)} \\ \;\;\;\; = \displaystyle\prod\limits_{j = 1}^l {x_j^0 \cdot {a_j} \cdot {b_j} + (1 - x_j^0) \cdot (1 - {a_j}} ) \cdot {b_j}, \\ \end{array} $
|
其中,
${c_{{i_h}}} = \displaystyle\prod\limits_{h' = 1,h' \ne r}^r {\frac{{ - {{\textit{z}}_{{i_{h'}}}}}}{{{{\textit{z}}_{{i_h}}} - {{\textit{z}}_{{i_{h'}}}}}}} $
. 对任意的
$a,{x_0} \in {\{ 0,1\} ^l}$
, 有
$a = $
$({a_1}, \cdots ,{a_l}),{x_0} = (x_1^0, \cdots ,x_l^0)$
, 若
$x \ne a$
, 则存在
$j \in {\rm{\{ }}1, \cdots ,l{\rm{\} }}$
使得
$x_j^0 \ne {a_j}$
, 因此
$y = f(0) = \prod\limits_{j = 1}^l {x_j^0 \cdot {a_j} \cdot {b_j} + (1 - x_j^0) \cdot }\left( {1 - } \right. $
$\left. {{a_j}} \right) \cdot {b_j} = 0. $
若
${x_0} = a$
, 对任意的
$j \in {{\rm{\{ 0,1\} }}^l}$
, 有
$x_j^0 = {a_j}$
, 则
$y = f(0) = \displaystyle\prod\limits_{j = 1}^l {x_j^0 \cdot {a_i} \cdot {b_i} + (1 - x_j^0) \cdot (1 - {a_i}} ) \cdot {b_i} = \prod\limits_{i = 1}^n {{b_i}} = b.$
因此
$y = \left\{ {\begin{array}{*{20}{c}} {0,x \ne a} \\ {b,x = a} \end{array}} \right. = {f_{a,b}}({x_0})$
. 因为只需要
$r(r = 2lt + 1,$
$r < n)$
个参与者就可以重构出秘密函数
${f_{a,b}}$
在
${x^0}$
点处的函数值, 可以容忍
$n - r$
个参与者不参与重构.
2.2 TFSS方案的安全性分析
定理1. 若
$G{F_q}$
为
$q$
元有限域, 1λ为安全参数, 则TFSS
$(Gen,Eval,Dec)$
是关于秘密函数
${f_{a,b}}(x): {\{ 0,1\} ^l} \to $
${\{ 0,1\} ^m}$
的信息论意义下
$t$
-安全的FSS方案.
证明: 假设
${\cal{A}}$
为任意具有无限计算能力的敌手则关于敌手
${\cal{A}}$
存在受贿参与者集合
$T \subseteq {\rm{\{ }}{P_1}{\rm{,}} \cdots {\rm{,}}{P_n}{\rm{\} }}$
, 且
$|T| = t$
(为了简便起见我们不妨取
$T = \{ {P_1}, \cdots ,{P_t}\} $
)的不可区分性实验
$\prod $
, 描述如下:
(1) 敌手
${\cal{A}}$
输入安全参数1λ输出
$({f_{{a^0},{b^0}}},{f_{{a^1},{b^1}}})$
, 满足
${a^0},{a^1} \in {\{ 0,1\} ^l},{b^0},{b^1} \in {\{ 0,1\} ^m}$
, 并将
$({f_{{a^0},{b^0}}},{f_{{a^1},{b^1}}})$
发送给挑战者
${\cal{C}}$
.
(2) 挑战者
${\cal{C}}$
收到
$({f_{{a^0},{b^0}}},{f_{{a^1},{b^1}}})$
后, 随机地产生挑战值
$c \in \{ 0,1\} $
, 执行子函数生成算法输入
${f_{{a^c},{b^c}}}$
, 输出
$(k_1^c, \cdots ,k_n^c)$
, 并将
${{\rm{\{ }}k_i^c{\rm{\} }}_{i \in T}}$
发送给敌手
${\cal{A}}$
.
(3) 敌手
${\cal{A}}$
收到
${{\rm{\{ }}k_i^c{\rm{\} }}_{i \in T}}$
后, 根据自己所掌握的信息给出一个关于挑战值
$c$
的猜测
$\hat c$
.
在上述实验
$\prod $
中, 敌手
${\cal{A}}$
从受贿参与者集合
$T = \{ {P_1}, \cdots ,{P_t}\} $
中收到了
$t$
个子函数
${{\rm{\{ }}k_i^c{\rm{\} }}_{i \in T}}$
, 其中子函数
$k_u^c = (g_{1,u}^c{\rm{,}} \cdots {\rm{,}}g_{l,u}^c{\rm{,}}\hat g_{1,u}^c{\rm{,}} \cdots {\rm{,}}\hat g_{l,u}^c{\rm{)(}}u = 1, \cdots ,t{\rm{)}}$
.
|
$ \left\{ \begin{array}{l} \!\!\!\!\!g_{j,u}^c \!=\! (a_j^c \!+\! {r_{j,1}} \cdot {{\textit{z}}_u} \!+\! \cdots \!+\! {r_{j,t}} \cdot {\textit{z}}_u^t) \cdot (b_j^c \!+\! {r_{j,1}} \!\cdot\! {{\textit{z}}_u} \!+\! \cdots \!+\! {r_{j,t}} \!\cdot\! {\textit{z}}_u^t)\\ \!\!\!\!\!\hat g_{j,u}^c \!\!=\!\! (\!1 \!-\! (a_j^c \!+\! {r_{j,1}} \!\cdot\! {{\textit{z}}_u} \!+\!\! \cdots \!\!+\! {r_{j,t}}\! \cdot\! {\textit{z}}_u^t)) \cdot (b_j^c \!+\!\! {r_{j,1}} \!\cdot\! {{\textit{z}}_u} \!+\!\! \cdots \!\!+\! {r_{j,t}}\! \cdot\! {\textit{z}}_u^t) \end{array} \right.\!\!\!\! $
|
此时敌手
${\cal{A}}$
可以通过子函数
$k_u^c$
计算
${w_{j,u}} = g_{j,u}^c + \hat g_{j,u}^c = $
$ b_j^c + {r_{j,1}} \cdot {{\textit{z}}_u} + \cdots + {r_{j,t}} \cdot {\textit{z}}_u^t,$
$j = 1, \cdots ,l,u = 1, \cdots ,t$
, 满足以下等式关系:
|
$\begin{array}{l} \underbrace {\left( {\begin{array}{*{20}{c}} {b_1^c}&{b_1^c}& \cdots &{b_1^c} \\ {b_2^c}&{b_2^c}& \cdots &{b_2^c} \\ \vdots & \vdots &{}& \vdots \\ {b_l^c}&{b_l^c}& \cdots &{b_l^c} \end{array}} \right)}_B + \underbrace {\left( {\begin{array}{*{20}{c}} {{r_{1,1}}}&{{r_{1,2}}}& \cdots &{{r_{1,t}}} \\ {{r_{2,1}}}&{{r_{2,2}}}& \cdots &{{r_{2,t}}} \\ \vdots & \vdots &{}& \vdots \\ {{r_{l,1}}}&{{r_{l,2}}}& \cdots &{{r_{l,t}}} \end{array}} \right)}_R\underbrace {\left( {\begin{array}{*{20}{c}} {{{\textit{z}}_1}}&{{{\textit{z}}_2}}& \cdots &{{{\textit{z}}_t}} \\ {{{\textit{z}}_1}^2}&{{{\textit{z}}_2}^2}& \cdots &{{{\textit{z}}_t}^2} \\ \vdots & \vdots &{}& \vdots \\ {{{\textit{z}}_1}^t}&{{{\textit{z}}_2}^t}& \cdots &{{{\textit{z}}_t}^t} \end{array}} \right)}_Z = \underbrace {\left( {\begin{array}{*{20}{c}} {{w_{1,1}}}&{{w_{1,2}}}& \cdots &{{w_{1,t}}} \\ {{w_{2,1}}}&{{w_{2,2}}}& \cdots &{{w_{2,t}}} \\ \vdots & \vdots &{}& \vdots \\ {{w_{l,1}}}&{{w_{l,2}}}& \cdots &{{w_{l,t}}} \end{array}} \right)}_W \\ \end{array} $
|
因为Z为非退化矩阵, R为一个随机矩阵, 所以对于敌手
${\cal{A}}$
来说矩阵W为一个随机矩阵, 则敌手
${\cal{A}}$
不能得到
$b_j^c(j = 1, \cdots ,l)$
的任何信息. 又因为:
|
$ \left\{ \begin{array}{l} \!\!\!\!\!g_{j,u}^c \!=\! (a_j^c \!+\! {r_{j,1}} \cdot {{\textit{z}}_u} \!+\! \cdots \!+\! {r_{j,t}} \cdot {\textit{z}}_u^t) \cdot (b_j^c \!+\! {r_{j,1}} \cdot {{\textit{z}}_u} \!+\! \cdots \!+\! {r_{j,t}} \cdot {\textit{z}}_u^t)\\ \!\!\!\!\!\hat g_{j,u}^c \!\!=\! (\!1 \!\!-\! (a_j^c \!+\! {r_{j,1}}\! \cdot \!{{\textit{z}}_u} \!+\!\! \cdots \!\!+\! {r_{j,t}}\! \cdot\! {\textit{z}}_u^t)) \cdot (b_j^c \!+\! {r_{j,1}}\! \cdot\! {{\textit{z}}_u} \!+\!\! \cdots \!\!+\! {r_{j,t}}\! \cdot\! {\textit{z}}_u^t) \end{array} \right.\!\!\!\! $
|
则敌手
${\cal{A}}$
不能得到
$a_j^c,b_j^c,(c \in \{ 0,1\} )$
的任何信息, 进而敌手
${\cal{A}}$
不能得到关于挑战值
$c$
的任何信息. 所以
$Adv({1^\lambda }, $
$A,T) = Pr [\hat c = c] - \dfrac{1}{2} = 0$
. 则定理1得证.
2.3 TFSS方案的通信复杂度分析
在方案TFSS中
${k_i} = ({g_{1,i}}, \cdots ,{g_{l,i}};{\hat g_{1,i}}, \cdots ,{\hat g_{l,i}})(i = $
$1,\cdots ,n) $
, 其
${g_{j,i}} = {g_j}({{\textit{z}}_i}),{\hat g_{j,i}} = {\hat g_j}({{\textit{z}}_i}) \in {F_q}$
, 因此
${\rm{|}}{k_i}{\rm{|}} = {\rm{2}}l \cdot \log _2^q$
. 因为
${y_i} \in {F_q}$
, 则
${\rm{|}}{y_i}{\rm{|}} = {\rm{log}}_{\rm{2}}^q$
. 因此
$\Psi = \displaystyle\sum\limits_{i = 1}^n {|{k_i}|} + \sum\limits_{h = 1}^r {|{y_{{i_h}}}|} = $
$ (2nl + h) \cdot \log _2^q$
. 因为
$(n,r,\log _2^q)$
为常数, 则
$\Psi = {\rm O}(l)$
.
3 文献[11]的方案及其分析
本节对文献[11]构造的方案进行了具体的描述, 并对其方案的不满足方案所定义的t-安全性的原因进行了具体的分析.
3.1 文献[11]的方案
为了解决现有FSS方案不具有门限的问题, 文献[11]给出了秘密函数为
${f_{a,b}}(x):{\{ 0,1\} ^l} \to G{F_q}$
,
$n$
为参与者的个数,
$t(t = l + 1,t < n)$
为重构门限的FSS方案在其方案中发送者D将
$a \in {{\rm{\{ 0,1\} }}^l}$
转换为二进制表示, 则
$a = $
$ ({a_1}, \cdots ,{a_l})$
, 令
$b = \prod\limits_{j = 1}^l {{b_j}} $
, 其中
${b_j} \in G{F_q}$
. 发送者D从
$G{F_q}$
中随机均匀地选取
$l$
个值
${r_1}, \cdots ,{r_l}$
, 生成
$2l$
个关于z的一次多项式
$\left\{ {\begin{array}{*{20}{l}} {{g_j}({\textit{z}}) = ({r_j} \cdot {\textit{z}} + {a_j}) \cdot {b_j}} \\ {{{\hat g}_j}({\textit{z}}) = (1 - ({r_j} \cdot {\textit{z}} + {a_j})) \cdot {b_j}} \end{array}} \right.$
. 之后D使用公开值
${{\textit{z}}_1}, \cdots ,{{\textit{z}}_n}$
计算
${g_{j,i}} = {g_j}({{\textit{z}}_i}),{\hat g_{j,i}} = {\hat g_j}({{\textit{z}}_i})(i = 1, \cdots ,n)$
, 并生成
${k_i} = ({g_{1,i}}, \cdots ,{g_{l,i}};{\hat g_{1,i}}, \cdots ,{\hat g_{l,i}})$
. 之后D将生成的
${k_i}$
发送给参与者
${P_i}$
. 参与者
${P_i}$
收到
${k_i} = ({g_{1,i}}, \cdots ,{g_{l,i}};{\hat g_{1,i}}, \cdots ,{\hat g_{l,i}})$
后, 对于任意的
${x_0} \in {\{ 0,1\} ^l}$
, 将
${x_0}$
用二进制表示为
${x_0} = $
$ (x_1^0, \cdots ,x_l^0)$
. 并计算
${y_i} = \displaystyle\prod\limits_{j = 1}^l {(x_j^0 \cdot {g_{j,i}} + (1 - x_j^0)(1 - {{\hat g}_{j,i}}))} $
. 在重构阶段任意
$t$
个参与者
${P_{{i_u}}}(u = 1, \cdots ,t)$
通过
$y = $
$ \displaystyle\sum\nolimits_{u = 1}^t {{c_{{i_u}}} \cdot {y_{{i_u}}}} $
计算出秘密函数
${f_{a,b}}$
在
${x_0}$
点处的函数值, 其中,
${c_{{i_u}}} = \displaystyle\prod\limits_{u' = 1,u' \ne u}^t {\dfrac{{ - {{\textit{z}}_{{i_{u'}}}}}}{{{{\textit{z}}_{{i_u}}} - {{\textit{z}}_{{i_{u'}}}}}}} $
.
正确性: 在文献[11]方案中存在关于z的l次多项式
$f({\textit{z}}) = \displaystyle\prod\limits_{j = 1}^l {(x_j^0 \cdot {g_j}({\textit{z}}) + (1 - x_j^0)(1 - {{\hat g}_j}(z)))} $
, 其常数项
$f(0) = $
$ \displaystyle\prod\limits_{j = 1}^l {(x_j^0 \cdot {a_j} \cdot {b_j} + (1 - x_j^0)(1 - {a_j} \cdot {b_j}))} $
, 对于任意的
${x_0} \in {\{ 0,1\} ^l}$
, 若
${x_0} \ne a$
, 则存在
$x_j^0 \ne {a_j}$
, 因此有
$f(0) = 0$
. 若
${x_0} = a$
, 则对任意的
$(j = 1, \cdots ,l)$
都有
$x_j^0 = {a_j}$
, 因此有
$f(0) = \displaystyle\prod\limits_j^l {{b_j}} = b$
. 所以
$f(0) = \left\{ {\begin{array}{*{20}{c}}{0,{x_0} \ne a}\\{b,{x_0} = a}\end{array}} \right.$
, 因此关于
${\textit{z}}$
的
$l$
次多项式
$f(z)$
的常数项
$f(0) = {f_{a,b}}({x_0})$
. 而每个参与者
${P_i}$
通过
${k_i}(i = 1, \cdots ,n)$
计算的值
${y_i} = \displaystyle\prod\limits_{j = 1}^l {(x_j^0 \cdot {g_{j,i}} + (1 - x_j^0)(1 - {{\hat g}_{j,i}}))} = f({{\textit{z}}_j})$
. 因此任意
$t(t = l + 1,t < n)$
个参与者可以通过多项式插值计算出
$f(0)$
, 进而重构出秘密函数
${f_{a,b}}$
在点
${x_0}$
处的函数值.
通过分析发现文献[11]的方案在保证方案正确重构的前提下, 其方案可以容忍
$n - t$
个参与者不参与重, 因此其方案可以更加灵活地应用到现实场景.
3.2 安全性分析
本小节对文献[11]方案的安全性进行分析. 详细分析了每个参与者如何通过自己的子函数来计算得到秘密函数
${f_{a,b}}$
中b的值, 以及任意两个参与者联合如何计算得到整个秘密函数
${f_{a,b}}$
, 具体过程如下:
1) 参与者
${P_i}(i = 1, \cdots ,n)$
, 通过
${k_i}$
计算秘密函数
${f_{a,b}}$
中b的值.
在文献[11]的方案中
${k_i} = ({g_{1,i}}, \cdots ,{g_{l,i}};{\hat g_{1,i}}, \cdots ,{\hat g_{l,i}})$
, 其中
${g_{j,i}} = {g_j}({{\textit{z}}_i}) = ({r_j} \cdot {{\textit{z}}_i} + {a_j}) \cdot {b_j}$
,
${\hat g_{j,i}} ={\hat g_j}({{\textit{z}}_i}) = (1 - ({r_j} \cdot$
$ {{\textit{z}}_i} + {a_j})) \cdot {b_j}$
, 任意的参与者
${P_i}$
计算
${b_j} = {g_{j,i}} + {\hat g_{j,i}}(j = 1, \cdots ,l)$
, 从而得到
$b = \displaystyle\prod\limits_{j = 1}^l {{b_j}} $
.
2) 任意两个参与者(不妨设为
${P_1},{P_2}$
)联合通过
${k_1},{k_2}$
计算出秘密函数
${f_{a,b}}$
.
参与者
${P_1}$
收到子函数
${k_1} = ({g_{1,1}}, \cdots ,{g_{l,1}};{\hat g_{1,1}}, \cdots , $
${\hat g_{l,1}})$
, 参与者
${P_2}$
收到子函数
${k_2} = ({g_{1,2}}, \cdots ,{g_{l,2}};{\hat g_{1,2}}, \cdots ,{\hat g_{l,2}})$
, 由1)中的分析可知, 参与者
${P_1}$
,
${P_2}$
分别通过子函数
${k_1}$
,
${k_2}$
计算出
${b_j}(j = 1, \cdots ,l)$
. 此时参与者
${P_1}$
利用计算得到的
${b_j}$
, 子函数
${k_1}$
,
${k_2}$
和公开值
${{\textit{z}}_1}$
,
${{\textit{z}}_2}$
计算
${r_j} = \dfrac{{{g_{j,2}} - {g_{j,1}}}}{{{b_j}({{\textit{z}}_2} - {{\textit{z}}_1})}}$
, 同样参与者
${P_2}$
利用计算得到的
${b_j}$
, 子函数
${k_1}$
,
${k_2}$
和公开值
${{\textit{z}}_1}$
,
${{\textit{z}}_2}$
计算
${r_j} = \dfrac{{{g_{j,2}} - {g_{j,1}}}}{{{b_j}({{\textit{z}}_2} - {{\textit{z}}_1})}}$
, 随后
${P_1}$
计算
${a_j} = \frac{{{g_{j,1}}}}{{{b_j}}} - {r_j}{{\textit{z}}_1}$
.
${P_2}$
计算
${a_j} = \dfrac{{{g_{j,2}}}}{{{b_j}}} - {r_j}{{\textit{z}}_2}$
. 此时参与者
${P_1}$
,
${P_2}$
可以分别独自计算出
$a = ({a_1}, \cdots ,{a_l})$
.
基于上述分析可知, 在文献[11]方案中任意两个参与者联合可以通过子函数和公开值计算出
$a$
,
$b$
的值, 从而得到秘密函数
${f_{a,b}}$
且任意参与者可以通过子函数计算得到秘密函数
${f_{a,b}}$
中b的值. 所以其方案不能抵抗t个参与者的联合, 因此不满足FSS方案中所定义的t-安全性.
3.3 通信复杂度分析
在文献[11]的方案中
${k_i} = ({g_{1,i}}, \cdots ,{g_{l,i}};{\hat g_{1,i}}, \cdots ,{\hat g_{l,i}}) $
$(i = 1, \cdots ,n)$
, 其
${g_{j,i}} = {g_j}({{\textit{z}}_i}),{\hat g_{j,i}} = {\hat g_j}({{\textit{z}}_i}) \in G{F_q}$
, 因此
${\rm{|}}{k_i}{\rm{|}} = {\rm{2}}l \cdot \log _2^q$
. 因为
${y_i} \in {F_q}$
, 则
${\rm{|}}{y_i}{\rm{|}} = {\rm{log}}_{\rm{2}}^q$
. 因此
$\Psi = $
$ \displaystyle\sum\limits_{i = 1}^n {|{k_i}|} + \sum\limits_{u = 1}^t {|{y_{{i_u}}}|} = (2nl + t) \cdot \log _2^q$
. 因为
$(n,t,\log _2^q)$
为常数, 则
$\Psi = O(l)$
.
4 TFSS方案与现有FSS方案的比较
本节我们将本文构造的基于多项式插值的门限函数秘密分享TFSS方案与现存的文献[5,6,9,11]中的FSS方案在方案所基于的工具, 有无门限值特性, 方案的安全性的级别以及方案的通信复杂度4个方面进行全面的比较. 为了比较的方便, 假设所有FSS方案分享的秘密函数均为点函数
${f_{a,b}}(x):{\{ 0,1\} ^l} \to G{F_q}$
,
$\lambda $
表示伪随机生成器种子的长度, t表示重构门限值, n表示参与者的个数. 具体比较结果见表1.
表 1(Table 1)
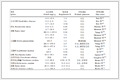
表 1 TFSS方案与现有FSS方案的比较
| 方案 |
基于的工具 |
(门限值, 参与者个数) |
安全性 |
通信复杂度 |
| 文献[5]
|
伪随机生成器 |
(2,2) |
计算意义下t-安全
|
${\rm O}(\lambda {l^{\log _2^3}})$
|
| 文献[6]
|
伪随机生成器 |
(2,2) |
计算意义下t-安全
|
${\rm O}(\lambda l)$
|
| 文献[6]
|
伪随机生成器 |
$(n,n)$
|
计算意义下t-安全
|
${\rm O}(\lambda {2^{{{(l + n - 1)} / 2}}})$
|
| 文献[9]
|
伪随机生成器 |
(2,2) |
计算意义下t-安全
|
${\rm O}(\lambda l)$
|
| 文献[11]
|
多项式 |
$(t,n)$
|
无安全性 |
${\rm O}(l)$
|
| TFSS |
多项式 |
$(r,n)$
|
信息论意义下t-安全
|
${\rm O}(l)$
|
|
表 1 TFSS方案与现有FSS方案的比较
|
经过比较发现本文构造的TFSS方案相对于文献[5,6,9]中构造的FSS方案具有额外的门限特性, 即在重构的过程中可以容忍参
$(n - r)$
个参与者不参与, 因此可以更加灵活地应用于现实场景, 且在安全性级别上由2.2节中对TFSS方案的安全性证明可得其为信息论意义下
$t$
-安全的, 而文献[5,6,9]中构造的FSS方案构造均基于伪随机生成器, 所以其方案的安全性基于密码学中单向函数的存在性假设, 进而为计算意义下t-安全的. 因此TFSS方案相对于文献[5,6,9]中构造的FSS方案具有更高级别的安全性. 此外在分享的秘密函数均为
${f_{a,b}}(x):{\{ 0,1\} ^l} \to G{F_q}$
的前提下, 由2.3节对TFSS方案的通信复杂的分析可得, TFSS方案的通信复杂度为
${\rm O}(l)$
, 低于文献[5,6,9]中构造的FSS方案的通信复杂度. 在与文献[11]中构造的FSS方案对比中可以发现, 虽然TFSS方案与文献[11]中构造的FSS方案均具有门限的特性, 且具有相同级别的通信复杂度. 但在安全性上经过3.3节对文献[11]中构造的FSS方案的安全性分析可得, 其方案不具有FSS方案定义的t-安全性, 而本文构造的TFSS方案具有信息论意义下t-安全性.
5 结语
本文针对现有的函数秘密分享方在重构阶段需要所有参与者参与不能灵活的适用于现实场景的问题, 采用多项式技术构造了门限函数秘密分享方案. 并按照函数秘密分享方案定义的安全模型证明了新构造的门限函数秘密分享方案为信息论意义下安全的. 并对文献[11]构造了门限函数秘密分享方案进行的分析, 指出了其方案存在安全性漏洞. 最后本文将新构造的门限函数秘密分享方案与现有的函数秘密分享方案进行了比较, 发现其具有更高级别的安全性和更高的效率. 但事实上, 本文构造的门限函数秘密分享方案的门限值r是受限的, 要求
$r = 2lt + 1$
. 因此在未来是否能构造出门限值自由的函数秘密分享方案是一个值得继续思考的问题.
 2020, Vol. 29
2020, Vol. 29


