数据中心的负载均衡问题一直是数据中心研究的热点问题, 追根究底, 主要原因是资源配置问题^[1], 即资源利用不均衡问题. 面对由大量异构设备组成的数据中心, 如何实现其负载均衡成为研究热点问题. 虚拟机迁移技术是解决数据中心资源分配问题的有效解决方法, 其在提供平台有效服务的情况下对节点虚拟机资源进行调整, 以提高平台资源利用率, 保证服务质量, 是实现数据中心负载均衡的有效手段之一^[2-4].

1 基于虚拟机迁移的负载均衡策略 1.1 相关介绍

基于虚拟机迁移技术的负载均衡策略, 即将负载过高或过低的节点服务器进行相应的虚拟机迁移操作, 通过调整节点服务器负载, 达到整个平台的负载均衡^[3]. 由于任务到达具有随机性, 节点的负载也是不断变化的, 若想实现数据中心的负载均衡, 则需一套虚拟机动态迁移策略, 通过监测数据中心节点的负载状况, 动态地进行虚拟机迁移调整^[4], 从而提高节点资源利用率, 改善数据中心的负载均衡.

虚拟机迁移过程可以分为两大模块: 迁移触发时机与迁移选择策略. 迁移时机触发策略即根据节点资源使用状态判断是否达到迁移条件, 从而触发下一模块; 迁移选择策略包括选择待迁移虚拟机和目标节点, 即确定待迁移虚拟机至其迁移目的节点的最佳方案.

迁移时机触发策略通常使用状态阈值法, 将每种状态设定阈值进行划分, 但在判断迁移时机时需要避免负载瞬时值影响时机判断的准确性, 从而避免由迁移时机不准确导致的过迁移现象. 状态阈值法分为静态阈值法与动态阈值法, 由于静态阈值法一经设定后不能根据资源使用状态动态调整, 故而存在适应性差和灵活度低问题. 文献[5]提供了一种根据数据中心整体负载量调整阈值窗口的迁移时机判决算法方法, 有效解决了由静态阈值造成的虚拟机频繁迁移问题. 文献[6]使用以调度频率和负载率作为反馈值的动态阈值法判定触发时机可以有效根据资源动态变化开启调度时机, 但是未考虑数据中心整体的负载度, 当数据中心接受大量任务时可能导致数据中心的整体负载度过高. 文献[7]使用负载预测的方法对未来几期的负载进行预测, 进而减少负载瞬时值的影响, 但触发时机的合理性由预测方法的准确性来决定, 虽复杂算法可以提高预测的准确性, 但是会增加计算资源的消耗.

迁移选择策略旨在快速解除节点过载状态, 即如何选择需迁移的虚拟机与目的节点, 在最少迁移代价与最少迁移时间的条件下将待迁移虚拟机迁移至目的节点, 调整节点资源状态, 使得数据中心回到负载均衡范围. 文献[8]使用采用最大相关性虚拟机选择算法(RRVMS)和多资源相关匹配目的主机选择算法(RMRHS)对虚拟机进行迁移, 即选择最大相关虚拟机迁移到资源最小相关的目的主机上, 可以有效减少迁移次数从而降低能耗, 但未考虑到迁移代价和负载均衡问题. 文献[9]根据虚拟机与服务器资源的相关性与资源权重比选择相关性大但带宽资源利用率低的虚拟机, 并考虑迁移数量以及资源匹配程度选择目标主机, 可以有效减少迁移代价. 但是该方法的迁移开销仅考虑了迁移次数, 具有一定的局限性.

针对以上问题, 本文设计了一种基于虚拟机动态迁移的负载均衡策略, 通过监控全局负载度与高低负载节点占比动态调整阈值从而实现对节点资源的状态评估与迁移时机判定; 使用基于负载类型感知的选择策略, 即通过考虑虚拟机与节点资源的依赖度和虚拟机贡献度选择待迁移虚拟机, 并根据虚拟机与目的节点的资源匹配度与迁移代价选择目的节点, 实现对高负载与低负载节点的虚拟机动态调整, 从而优化节点资源配置并改善数据中心负载均衡.

1.2 相关定义

本文考虑到异构节点的资源配置差异, 选取CPU使用率、内存使用率和带宽使用率作为负载指标, 并将过载情况分为三种类型: CPU过载型、内存过载型和带宽过载型^[10], 从而对节点负载情况进行评估, 相关定义如下:

定义1. 数据中心有n个节点, 第i个节点的资源配置为: ${r_i} = (cp{u_i},ra{m_i},ban{d_i})$ , 记节点i的CPU利用率为CU_i、内存利用率为 $R{U_i}$ 、带宽利用率为 $B{U_i}$ , 则节点i的负载向量 ${N_i}$ 为:

$ {N_i} = \left( {C{U_i},R{U_i},B{U_i}} \right) $

(1)

若各负载指标的权值为 ${K_i} = \left[ {{k_1}\;{k_2}\;{k_3}} \right]\;$ , 其中 ${k_1} + $ ${k_2} + {k_3} = 1$ . 则节点i的负载度为:

$L{d_i} = {N_i} \cdot {K_i} = {k_1} \times C{U_i} + {k_2} \times R{U_i} + {k_3} \times B{U_i}$

(2)

那么, 数据中心负载度即全局负载度可由数据中心所有开启的节点负载度的平均值表示, 公式如下:

$L{d_{dc}} = \frac{1}{n}\sum\limits_{i = 1}^n {L{d_i}} $

(3)

定义2. 设节点负载超过高位阈值 $Th{r_h}$ 为重载; 负载低于低位阈值 $Th{r_l}$ 为轻载; 负载位于两个阈值之间为适载. 则表示如下:

$Thr = \left\{ {Th{r_h},Th{r_l}|Th{r_h},Th{r_l} \in \left( {0,1} \right)} \right\}$

(4)

$Th{r_h} = \left( {Th{r_{\rm cpu}},Th{r_{\rm ram}},Th{r_{\rm band}}} \right)$

(5)

其中, $Th{r_{\rm cpu}}$ 、 $Th{r_{\rm ram}}$ 、 $Th{r_{\rm band}}$ 和分别为CPU、内存和带宽的高位阈值, 分别根据各自的利用率设定. $Th{r_l}$ 则根据节点负载度进行设定.

定义3. 低于低位阈值的节点集合为L; 将超过高位阈值的节点组成高负载节点矩阵H, 根据其过载类型使用节点状态标记进行区分, 表示如下:

$H = \left[ {\begin{array}{*{20}{c}} {N_{_1}^{\rm T}}&{{S_1}}&{Nu{m_1}} \\ {N_2^{\rm T}}&{{S_2}}&{Nu{m_2}} \\ \vdots & \vdots & \vdots \\ {N_{_n}^{\rm T}}&{{S_n}}&{Nu{m_n}} \end{array}} \right]$

(6)

其中, 第i行为第i个节点的各参数值; 第一行为节点的负载指标向量的转置; 第二列为节点状态标记, 值为1表示CPU利用率高, 值为2表示内存利用率高, 值为3表示带宽利用率高. 最后一位Num表示节点编号.

2 基于动态阈值的迁移时机判决算法

虚拟机迁移触发时机的选择至关重要, 针对现有的静态阈值的适应性差和灵活度低问题, 本文通过分析数据中心全局负载度、高负载比率和低负载比率对实现对阈值的动态调整, 从而增加迁移触发策略的灵活性与触发时机的合理性.

2.1 动态阈值调整方案

(1) 考虑因素

本文阈值动态调整方案考虑因素共有3个: 数据中心负载度(全局负载度)、高负载比率和低负载比率. 下面介绍3种因素的求解方法及对其数据中心的影响.

① 全局负载度

全局负载度是评价数据中心整体负载情况的有效方法之一. 当全局负载度过高时, 数据中心整体接收大量的负载任务, 此时需增加可用资源承接负载任务以均衡全局负载; 当全局负载度过低时, 数据中心接收的负载任务减少, 此时需缩减可用资源范围. 全局负载度计算方法如下:

取t时段内的负载信息并根据公式(3)得到此时段内负载度集合 $\left\{ {L{d_{dc}}(1),L{d_{dc}}(2), \cdot \cdot \cdot ,L{d_{dc}}(t)} \right\}$ ; 为了减小负载瞬时值的影响, 剔除该集合中的m个孤立点, 此时负载度集合为 $\left\{ {L{d_{dc}}(1),L{d_{dc}}(2), \cdot \cdot \cdot ,L{d_{dc}}(t - m)} \right\}$ , 再采用权重法计算全局负载度, 如下:

$L{d_{dc}} = \sum\limits_{i = 1}^{t - m} {{l_i} \cdot L{d_{dc}}\left( i \right)} $

(7)

其中, ${l_1} + {l_2} + \cdot \cdot \cdot + {l_{t - m}} = 1$ , 权重系数 ${l_i}$ 按指数递增, 公式为:

${l_i} = {{{e^i}} / {\sum\limits_{j = 1}^m {{e^j}} }}$

(8)

为保持数据中心负载均衡度, 需为数据中心设置负载均衡范围 $\left( {{\omega _l},{\omega _h}} \right)$ , 此范围内数据中心负载度为适宜的, 此范围取值依据为数据中心此时段历史负载度.

② 高负载比率与低负载比率

高低负载节点比率表现出数据中心节点利用率情况. 当高负载节点数量过多时, 会多次触发迁移操作, 造成虚拟机频繁迁移, 造成资源浪费, 此时需要适量调高高位阈值或开启新的节点服务器; 低负载节点比率过多时, 此时数据中心过多服务器资源处于未充分利用状态, 故调低低位阈值并关闭部分节点服务器. 设高负载比率、低负载比率分别为 $L{r_h}$ 和 $L{r_l}$ , 权重系数 ${l_i}$ 计算见式(9), 在t时间段内, 计算公式如下:

$\left\{ \begin{array}{l} \begin{array}{*{20}{c}} {L{r_h} = \displaystyle\sum\limits_{i = 1}^t {{l_i} \cdot L{r_h}(i)} } & {{N_{itype}} > Th{r_{type}}} \end{array}\\ \begin{array}{*{20}{c}} {L{r_l} = \displaystyle\sum\limits_{i = 1}^t {{l_i} \cdot L{r_l}(i)} } & {L{d_i} < Th{r_l}} \end{array} \end{array} \right.$

(9)

设置高负载比率 $\left( {\min L{r_h},\max L{r_h}} \right)$ 和低负载比率范围 $\left( {\min L{r_l},\max L{r_l}} \right)$ 以判断调整阈值和开启或关闭节点的时机.

(2) 调整流程

通过全局负载度与高低负载节点比率实现对状态阈值的动态调控流程如下:

当 $L{d_{dc}} \notin \left( {{\omega _l},{\omega _h}} \right)$ 时, 若 $\min L{r_l} < L{r_l} < \max L{r_l}$ 或 $\min L{r_h} < L{r_h} < \max L{r_h}$ 时, 此时需进行阈值调整, 调整公式如下:

$\left\{ \begin{array}{l} Th{r_h} = Thr_h' + \left[ {{\tau _h}\dfrac{{L{d_{dc}}}}{{Ld_{dc}'}} - \left( {1 - {\tau _h}} \right)L{r_h}} \right] \times Thr_h'\\ Th{r_l} = Thr_l' + \left[ { - {\tau _l}\dfrac{{L{d_{dc}}}}{{Ld_{dc}'}} + \left( {1 - {\tau _d}} \right)\left( {L{r_h} - L{r_l}} \right)} \right] \times Thr_l' \end{array} \right.$

(10)

其中, $Thr_h'$ 、 $Thr_l'$ 分别表示调整前的高位阈值和低位阈值, ${\tau _h}$ 和 ${\tau _l}$ 分别为高位和低位阈值的调节因子, 当 $L{d_{dc}} < {\omega _{\rm{l}}}$ 时, ${\tau _h}$ 和 ${\tau _l}$ 皆为正数, 当 $L{d_{dc}} > {\omega _h}$ 时, ${\tau _h}$ 和 ${\tau _l}$ 皆为负数.

当 $L{d_{dc}} < {\omega _l}$ 且 $L{r_l} > \max L{r_l}$ 时, 数据中心负载度偏低, 此时需要选择需要进行迁移操作的部分轻载节点, 在轻载节点完成迁移操作后会关闭该节点. 确定待迁移(关闭)轻载节点列表方法如下:

首先将轻载节点按负载度进行升序, 此时轻载节点列表 $\left\{ {N{L_1},N{L_2}, \cdot \cdot \cdot ,N{L_s}} \right\}$ , 则对应节点负载值列表为 $\left\{ {L{d_1},L{d_2}, \cdot \cdot \cdot ,L{d_s}} \right\}$ , $L{d_{dc}}$ 为此时的全局负载度, n为正在使用的节点总数, 设需要关闭的节点为k个, 则k应该满足如下条件的最小正整数:

$\left\{ {\begin{array}{*{20}{l}} {n\left( {{\omega _l} - L{d_{dc}}} \right) < \displaystyle\sum\limits_{i = 1}^k {L{d_i}} } \\ {0 < k < n\left( {1 - \dfrac{{L{d_{dc}}}}{{{\omega _l}}}} \right) < s} \end{array}} \right.$

(11)

当 $L{d_{dc}} > {\omega _l}$ 且 $L{r_h} > \max L{r_h}$ 时, 数据中心负载度偏高, 此时开启一个新的节点.

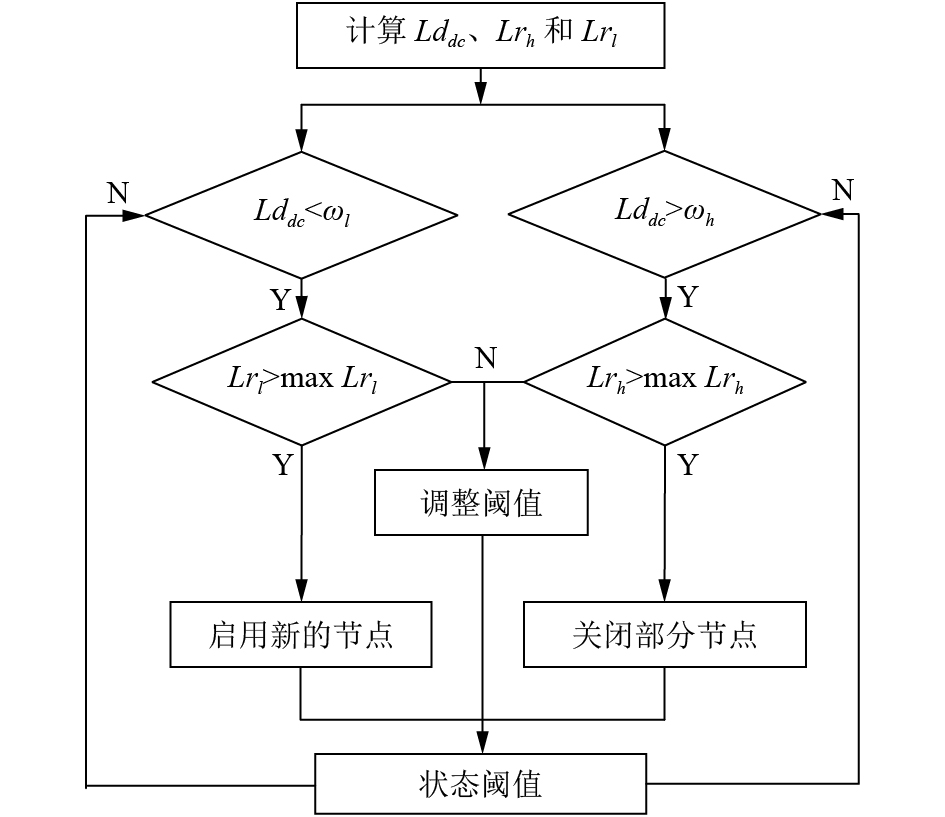
本文采用的动态阈值调整具体流程如图1所示.

2.2 迁移触发算法

由状态阈值可以对节点负载状态进行评估, 是判断节点是否需要进行迁移调整的重要步骤, 其评估结果是迁移触发时机判定的重要依据. 但是节点负载变化时会出现短时间内的负载抖动现象产生负载瞬时值, 进而影响迁移触发时机的判断, 降低虚拟机迁移的有效性. 本文采用乘积指数加权法^[11]对m期内的负载进行评估, 乘积指数加权公式如下:

$y = \prod\limits_{t \in {T_1}} {\dfrac{{x_t^{{w_t}}}}{{\mathop {\max }\limits_{t \in {T_1}} \left\{ {x_t^{{w_t}}} \right\}}}} \prod\limits_{t \in {T_2}} {\dfrac{{{{\left( {1 + \dfrac{1}{{{x_t}}}} \right)}^{{w_t}}}}}{{\mathop {\max }\limits_{t \in {T_2}} \left\{ {{{\left( {1 + \dfrac{1}{{{x_t}}}} \right)}^{{w_t}}}} \right\}}}} $

(12)

其中, ${w_t}$ 为第t期权重系数. 若此时为负载过载评估, 则 ${T_1}$ 为负载超过高位阈值的期数, ${T_2}$ 为负载低于高位阈值的期数; 若为负载轻载评估, 则 ${T_1}$ 为负载值低于低位阈值的期数, ${T_2}$ 为负载值高于低位阈值的期数.

根据以上状态阈值动态调整方法结合负载值评估方法, 设计了虚拟机的迁移时机判决算法, 内容如算法1.

算法1. 基于动态阈值的迁移时机判决算法

1) 收集各节点负载信息, 计算监测时间内全局负载度与高低负载节点占比, 判断是否需要更新阈值, 是则转第2)步, 否则转第3)步.

2) 分析全局负载度与高低负载占比, 调整并更新状态阈值.

3) 根据状态阈值, 分别判断各节点负载状态. 若节点负载指标高于高位负载, 开启该节点该负载指标过载评估, 转第4)步; 若节点负载度低于低位负载, 开启该节点负载度轻载评估, 转第5)步; 均未达到高低阈值要求为适载节点, 则转第7)步.

4) 对节点超过高位阈值的负载指标进行m期的查询并计算其评估值, 若评估值达到过载要求, 则判断此节点为该指标类型过载, 根据定义3, 更新高负载节点矩阵H. 转第3)步, 继续循环.

5) 对负载度低于低位阈值的节点进行m期的负载度查询并计算其评估值. 若m期内评估值均达到轻载要求, 则判断此节点轻载节点, 加入低负载节点列表.转第3)步, 继续循环.

6) 将低负载节点列表按负载度升序, 结合全局负载度, 判断是否在负载均衡范围 $\scriptstyle\left( {{\omega _l},{\omega _h}} \right)$ 中, 若 $\scriptstyle L{d_{dc}}\;< \;{\omega _{\rm{l}}}$ , 则根据式(11)计算得到待迁移操作的轻载节点集合L, 若 $\scriptstyle L{d_{dc}}\; >\; {\omega _l}$ 且 $\scriptstyle L{r_h} \;>\; \max L{r_h}$ , 则启用一个节点.

7) 输出高负载节点矩阵H与低负载节点矩阵L.

上述算法可以通过动态阈值判断迁移时机并得到高负载与低负载节点列表, 即确定需进行迁移选择策略的节点.

3 基于负载类型感知的迁移选择算法

基于动态阈值的迁移时机判决算法确定了需进行虚拟机迁移操作的高负载与低负载节点列表, 本节的迁移选择算法包含两个方面: 待迁移虚拟机的选择算法和目的节点的选择算法, 旨在选择合适的待迁移虚拟机与目的节点, 解除节点过载与轻载状态.

3.1 虚拟机选择算法

根据过载节点内所有虚拟机使用资源情况, 选择合适的待迁移在虚拟机迁移过程中至关重要. 本文将过载情况根据过载资源类型进行划分, 以最少迁移次数为目标, 那么待迁移虚拟机的选择即可描述为节点迁移走后某虚拟机后过载资源回到适载范围(即不超过此资源类型的高位阈值), 使用以下公式描述:

${N_{type}} - \overline {{V_{type}}} \le Th{r_{ type}}$

(13)

其中, ${N_{type}}$ 为节点资源为type类型的指标, $V = \left( \overline {{v_{\rm cpu}}} ,\right.$ $\left.\overline {{v_{\rm ram}}} ,\overline {{v_{\rm band}}} \right)$ 为虚拟机在n时段所使用的平均资源利用率向量. 除了满足此条件, 还需考虑其他方面因素, 如下:

(1)\虚拟机与节点的资源依赖度

考虑到最快解决过载状态, 引入虚拟机与节点的资源依赖度来评价虚拟机使用节点的资源情况, 按过载类型寻找该类型资源依赖度高的虚拟机. 虚拟机与节点的资源的依赖度 ${R_{type}}$ 定义如下:

${R_{type}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {{V_{type\;i}}{N_{type\;i}}} }}{{\sqrt {\left( {\displaystyle\sum\limits_{i = 1}^n {V_{type\;i}^2} } \right)\left( {\displaystyle\sum\limits_{i = 1}^n {N_{type\;i}^2} } \right)} }}$

(14)

其中, ${V_i}$ 为虚拟机在i时刻的某指标资源利用率, ${N_i}$ 为节点在i时刻的该指标资源利用率, ${R_{type}}$ 越大则表示该虚拟机与此节点的该指标类型资源的依赖越高.

(2) 虚拟机当前内存带宽比

虚拟机迁移的核心考虑因素是虚拟机内存页的迁移, 此外还易受到节点带宽因素的影响, 故而在迁移开销最小化的目的下选取虚拟机当前内存带宽较小的虚拟机, 公式如下:

${u_{rb}} = \sqrt {{{\left( {\frac{{{R_i}}}{{{B_i}}}} \right)}^2} - {{\left( {\frac{{{v_{{\rm ram}\;j}}}}{{{B_i}}}} \right)}^2}} $

(15)

其中, ${R_i}$ 为此节点i的可用内存; ${B_i}$ 为此节点i可用带宽; ${v_{{\rm ram}\;j}}$ 为虚拟机j的内存.

(3)虚拟机负载贡献度

虚拟机负载贡献度表现出此虚拟机使用此节点资源情况, 此值越大则表示该虚拟机使用的资源越多. 已知虚拟机在n时段所使用的平均资源利用率向量为V, 该节点的负载指标的权值为K, 则该虚拟机在此节点上的负载贡献度用式(16)描述:

$Lc = V \cdot K = {k_1} \times {v_{\rm cpu}} + {k_2} \times {v_{\rm ram}} + {k_3} \times {v_{\rm band}}$

(16)

若限定了某种资源类型Lc的值越大则代表另外虚拟机使用的两种资源越多.

由式(13)至式(16)可以得到影响虚拟机选择的3个指标值, 为了获得较少的迁移时间与迁移开销, 使用式(17)对这3个指标值进行处理.

$S = \sqrt {L{c^2} + u_{rb}^2 + {{\left( {\dfrac{1}{{{R_{type}}}}} \right)}^2}} $

(17)

选择待迁移虚拟机时将虚拟机按照此参考值升序排列, 选取此参考值小的虚拟机可获得最少的迁移次数、较少迁移时间与迁移代价.

为了方便为待迁移虚拟机选择目的节点(即下一小节), 为待迁移虚拟机计算资源比, 即以下公式:

$\dfrac{{{v_{\rm cpu}}}}{{CU}}:\dfrac{{{v_{\rm ram}}}}{{RU}}:\dfrac{{{v_{\rm band}}}}{{BU}}$

(18)

由虚拟机使用资源比可以得到此虚拟机的资源偏向类型.

考虑到以上问题, 本文以最快解决节点过载问题为目的, 选取迁移时间最短的虚拟机, 算法表达如算法2.

算法2. 待迁移虚拟机选择算法

1) 根据节点评估得到的高负载节点列表, 获取高负载节点信息.

2) 根据此节点过载类型, 根据式(13)计算一次迁移可使得该节点解除过载情况的待筛选虚拟机集合.

3) 根据式(14)计算待筛选虚拟机集合中各虚拟机的此类资源依赖度, 并按递减排序.

4) 根据式(15)计算各虚拟机的内存带宽比; 根据式(16)计算虚拟机的负载贡献度.

5) 根据式(17)选择虚拟机作为待迁移虚拟机并计算其资源比, 加入待迁移虚拟机列表.

若节点是由于轻载需进行迁移, 则直接获取其上运行的虚拟机, 计算其资源偏向比并加入待迁移虚拟机列表.

3.2 目的节点选择算法

目的节点的选取即为虚拟机选取合适的目的节点,即虚拟机安置问题, 高效的目的节点选择算法有利于提高整个平台的稳定性和资源的高效利用. 要考虑的因素主要有虚拟机与目的节点的资源匹配度以及迁移代价.

虚拟机与目标节点的资源匹配度主要用来度量节点剩余资源与待虚拟机所需资源的承接情况. 考虑到资源利用的均衡性, 依据虚拟机资源偏向优先为其配置该资源剩余度高的节点. 匹配度描述如下:

$M = \frac{{\displaystyle\sum\limits_{i = 1}^m {\sqrt {{{\left( {L{d_{_i}} - L{c_{_i}}} \right)}^2}} } }}{{\sqrt {\left( {{T_{\rm best}} - m} \right)} }}$

(19)

其中, m表示当前有m个虚拟机正在迁移到该台服务器上, ${T_{\rm best}}$ 为设定的节点承载虚拟机迁移的最大数目; $L{c_{_i}}$ 为第i个虚拟机的资源需求量;

选择目的节点必须要考虑的一个问题就是虚拟机的迁移代价, 这代表者虚拟机迁移过程中的资源损耗, 若是迁移代价过高, 则会造成资源浪费. 虚拟机到目的节点的迁移代价与两者距离有关, 其迁移代价由式(20)定义:

$C\left( {{V_i},{N_i}} \right) = \displaystyle\sum\limits_{i \ne j} {D\left( {{N_{i\;{\rm target}}},{N_{j\;{\rm src}}}} \right)} \cdot f\left( {{V_i},{V_j}} \right)$

(20)

其中, ${N_{i\;{\rm target}}}$ 指 ${V_i}$ 的目的节点, ${N_{j\;{\rm src}}}$ 为 ${V_i}$ 的源节点; $D\left( {{N_{i\;{\rm target}}},{N_{j\;{\rm src}}}} \right)$ 为 ${V_i}$ 到目的节点和源节点上剩余虚拟机 ${V_{\rm{j}}}$ 的通信距离; $f\left( {{V_i},{V_j}} \right)$ 为虚拟机之间的通信量.

根据以上内容, 设计目标节点选择算法表达可见算法3.

算法3. 目标节点选择算法

1) 根据节点评估得到的适载节点列表, 由负载度递增排序, 得到待选节点列表.

2) 根据式(19)计算待选节点列表计算虚拟机与节点的匹配度, 并按递减排序.

3) 按照匹配度顺序根据式(20)分别计算迁移代价.

4) 选取匹配度高且迁移代价最小的节点为目的节点.

4 实验验证与分析 4.1 实验准备

为了验证基于虚拟机动态迁移的负载均衡策略的有效性, 采用CloudSim 仿真平台进行仿真验证. 建立含有异构节点的数据中心, 并配置多规格虚拟机, 为使仿真使用的物理机和虚拟机负载更接近现实情况, 使用PlanetLab项目中提供的虚拟机监测数据作为实验负载, 模拟数据中心进行虚拟机迁移的仿真实验, 实验配置如表1.

为了比较本文策略的仿真效果, 使用以下指标对迁移策略的性能进行分析:

1) 虚拟机迁移次数. 实验中, 由于虚拟机个数、负载和位置的变化, 导致节点的负载动态变化, 虚拟机迁移策略影响着虚拟机的迁移次数, 故获取指定时间内的虚拟机迁移次数, 用来观测系统的虚拟机的迁移频率, 是判断虚拟机迁移策略性能的重要指标.

2) 数据中心平均负载度. 数据中心负载度是衡量数据中心负载情况与资源分配情况的有效指标, 若负载度保持较低水平则说明较多节点存在过多的空闲资源, 即资源分配不均衡, 若此指标数值过高, 则说明存在大量过载节点.

3)平均SLAV (Service Level Agreement Violation, SLAV). 平均 SLAV即平均服务等级协议违例率, 用来评价用户服务质量水平的常用指标之一, 该值越低则表示用户服务质量越高. 由于本文算法综合考虑了节点的CPU 资源、内存资源和带宽资源, 使用多维度平均SLAV计算方法, 如式(21):

$\overline {SLAV} = \frac{1}{k}\sum\limits_{j = 1}^n {\dfrac{1}{3}\left( {\sum\limits_{i = 1}^3 {\frac{{v_{iR}^{type} - v_{iA}^{type}}}{{v_{iR}^{type}}}} } \right) \times 100\% } $

(21)

其中, $v_{iR}^{type}$ 表示虚拟机需求的type类型资源量, $v_{iA}^{type}$ 为虚拟机type类型资源的实际使用量. K为一个周期内的违约次数.

4.2 实验分析

为了比较本文算法的仿真效果, 将使用两个对比方案进行实验对比. 对比方案分别为: 瞬时迁移触发策略搭配最大相关性选择策略的虚拟机迁移策略(以下称策略1)与文献[9]中的基于双门限与资源需求相关性匹配的虚拟机迁移算法(以下称策略2). 针对虚拟机迁移的两个模块进行两组实验, 第一组为迁移触发策略比较实验, 用以分析本策略中基于动态阈值的负载评估算法触发迁移时机的合理性; 第二组实验为迁移策略性能比对实验, 分析比较3种不同的迁移策略效果, 并对本文策略进行综合评价.

实验一. 迁移触发策略对比组

合理的迁移触发策略可以有效判断虚拟机迁移时机, 并通过触发时机的合理性减少由于节点负载不均衡导致的服务效率问题. 通常通过观测虚拟机迁移次数, 从而分析迁移触发策略的性能.

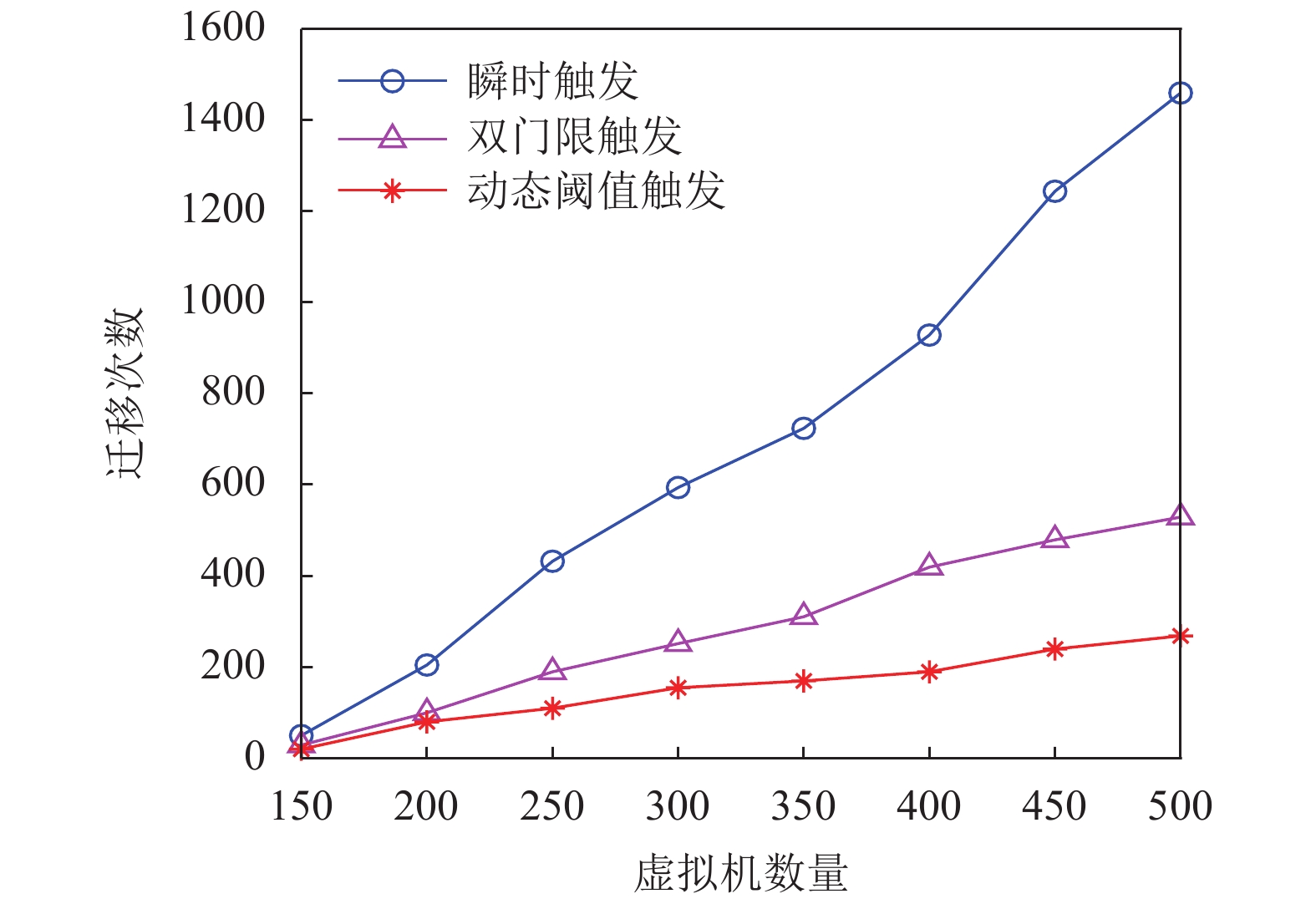
本实验组使用3种触发策略并在同一种选择策略的条件下进行实验, 通过收集一段时间内不同虚拟机数量下的虚拟机迁移次数进行可视化分析. 3种触发策略分别为: 策略1中的瞬时触发方式、策略2中的双门限触发方式和本文动态阈值触发方式. 实验结果如图2所示.

由图2可见, 随着虚拟机数目的增加, 3种触发策略下的虚拟机迁移次数也逐渐增加. 其中, 由瞬间触发策略下的虚拟机迁移频率曲线斜率最大且增长速度明显高于其他两种策略, 动态阈值触发策略下的虚拟机迁移频率最为平缓, 由此可见使用基于动态阈值的负载评估算法进行迁移时机判断更能有效减少由瞬时峰值导致的虚拟机迁移, 更有效解决由于虚拟机频繁迁移导致的资源浪费问题.

实验二. 迁移策略性能比对组

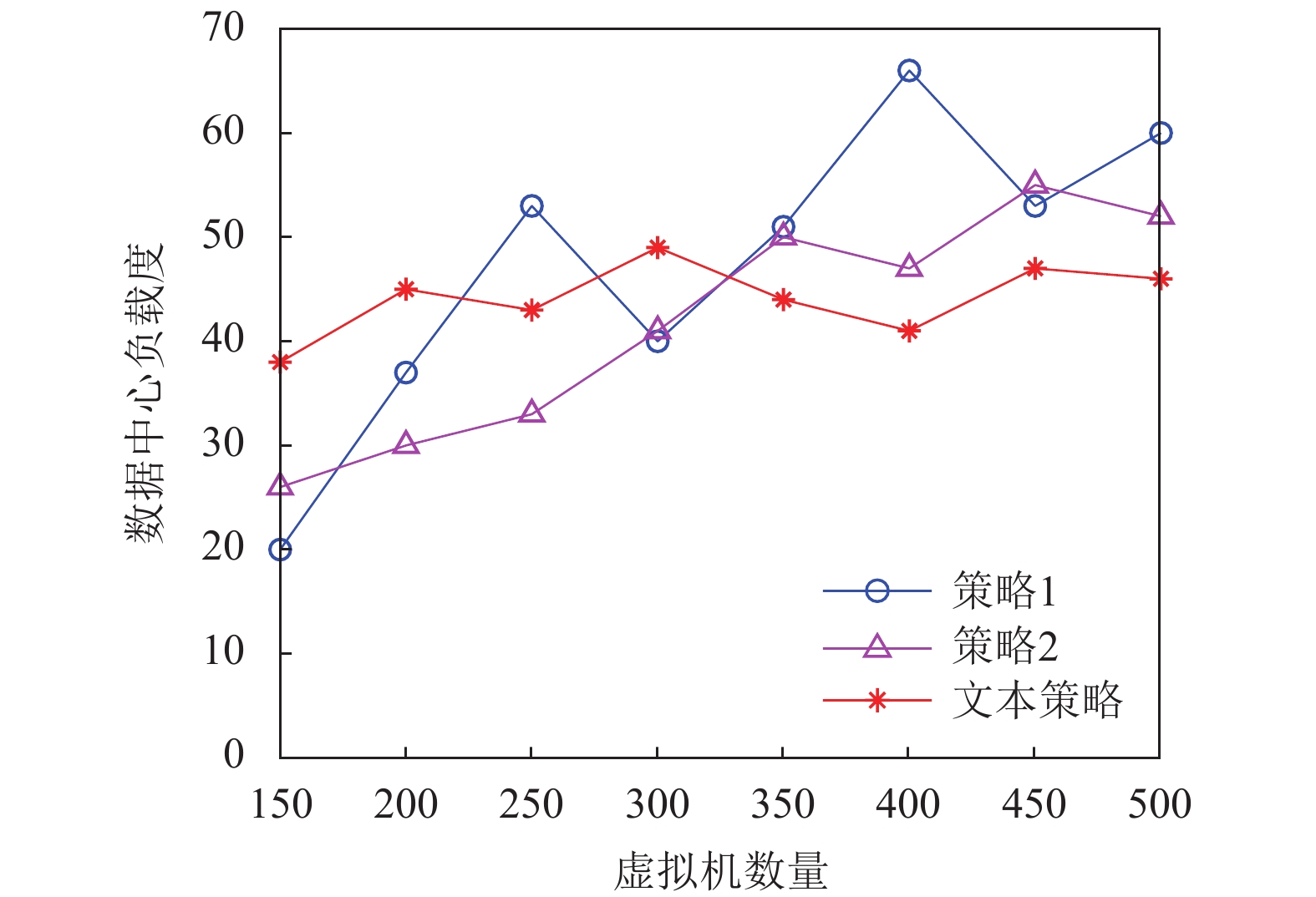
将本文迁移策略、策略1和策略2的实验效果进行分析比较, 主要从数据中心的负载度和平均SLAV进行比较. 不同虚拟机数量下的数据中心的负载度对比图如图3所示.

随着虚拟机数目的增加, 3种迁移策略下的数据中心负载度逐渐增加, 由策略1下的数据中心负载度曲线增长最快且波动最明显, 本文迁移策略下的数据中心负载度增长最慢且趋势平缓, 可见本文考虑虚拟机和节点过载资源的依赖关系和虚拟机负载贡献度的虚拟机选择算法配合根据虚拟机与目的节点资源匹配度和迁移代价的目的节点选择算法在保持数据中心负载均衡方面是有效的.

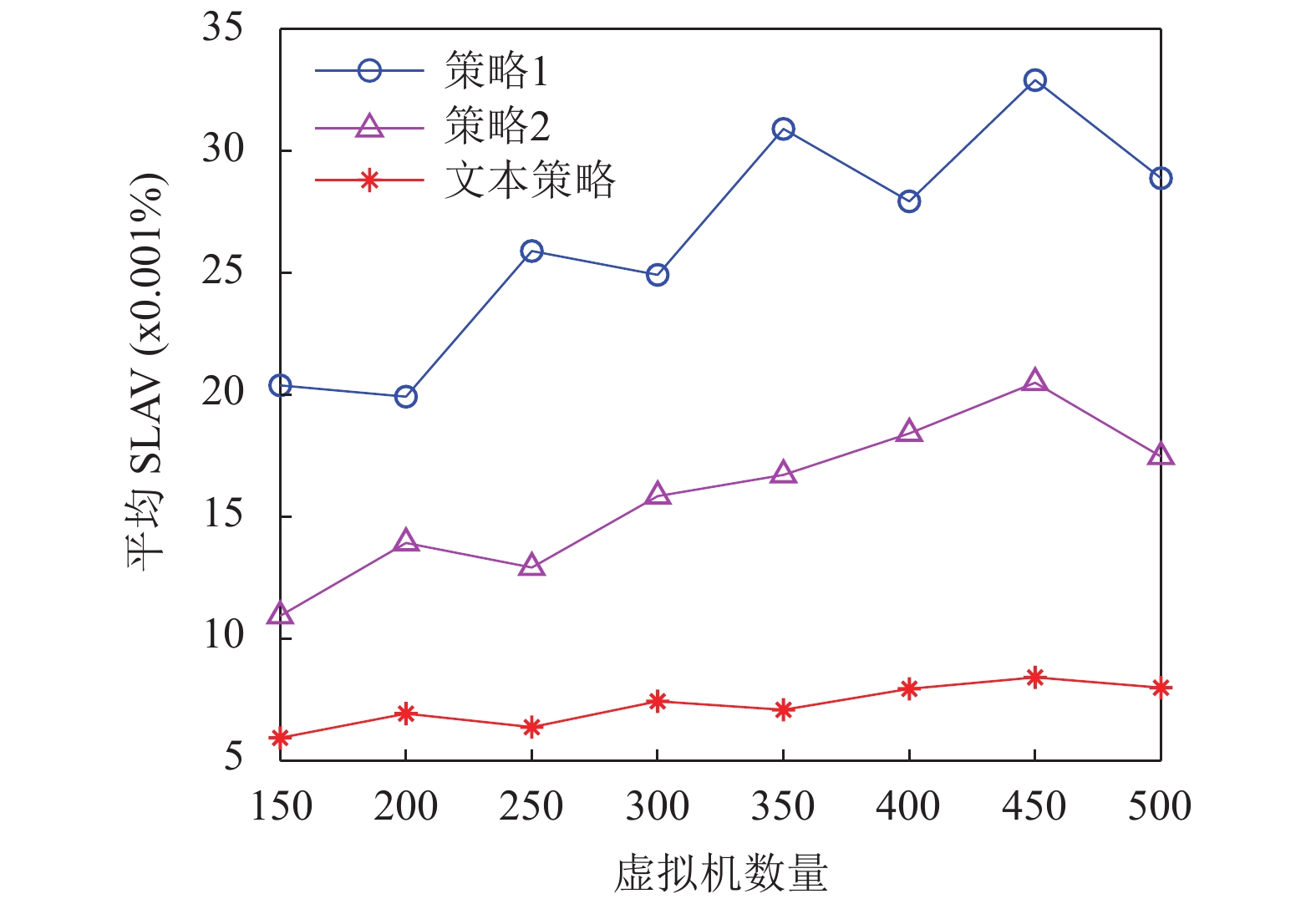
保证数据中心处于较高水平的服务质量也是评价虚拟机迁移策略效果的必要的指标. 本文通过分析平均SLAV对3种迁移策略下的服务质量进行评价, 不同虚拟机数量下的平均SLAV比较图如图4所示.

由图4可见, 随着虚拟机数目的增加, 3种迁移策略下的数据中心平均SLAV呈现不同程度的波动趋势, 策略1的平均SLAV曲线波动明显, 策略2其次, 本文策略具有最平稳的变化趋势, 由此可见, 本文策略可以有效地保证数据中心的SLAV的违背率, 并提供较为稳定的服务质量.

综上所述, 本文基于动态阈值的负载评估算法可以有效合理地对迁移时机进行判断并有效减少负载瞬时变化引起的迁移问题; 基于负载类型感知的选择策略包括根据虚拟机与节点过载资源的依赖关系与虚拟机负载贡献度的虚拟机选择算法与根据待迁移虚拟机与目的节点的资源匹配度与迁移代价的目的节点选择算法在保证服务质量与数据中心负载均衡方面是有效的.

5 结论与展望

本文针对数据中心异构节点设计了一种基于虚拟机动态迁移的负载均衡策略, 旨在通过解决异构节点钟各资源利用率不均衡问题达到数据中心负载均衡. 设计了基于动态阈值的负载评估算法用于判断迁移时机与基于负载类型感知的选择策略. 实验证明, 本文迁移策略可以有效减少虚拟机迁移频率, 保证服务质量并改善数据中心的负载均衡能力.