引言

电网可视化一直是电网中比较重要的研究课题. 在传统方式中, 不管是输电网接线图可视化还是厂站接线图可视化在实践中都耗费了大量的人力物力. 它们的实现方式往往是人工手动绘制或者初级的计算机自动绘制, 后期再加上较多的后期人工干预. 本文主要的研究对象是输电网接线图的自动生成. 电网接线图能够反映出厂站和线路之间的拓扑情况, 是电网的调度、检修、计划等部门常用的参考; 它在实际的实时调度和生产管理中有较多的应用. 近几年随着国家电网的快速发展, 厂站线路的数量规模越来越大, 计算机相关技术也在飞速发展, 利用计算机自动生成相关输电网接线图是现阶段研究的热点问题. 文献[1]是在能量管理系统(EMS)中实现了潮流图单线图的自动布局, 但并没有实现基于历史线路的问题的规划问题, 且线路规划算法也不相一致. 成图效果也存在不同.

而本文对厂站布局也是采用力导向算法^[2]; 而在线路规划中采用A*算法^[3]进行线路规划; 创新性的提出了评价算法反馈厂站布局进行微调再布线, 不断调整之后得到一个美观的厂站线路规划图. 同时, 算法还增加了在不改变历史厂站线路布局的情况下, 对新添加的厂站线路增量灵活布局的功能, 保证了历史数据的稳定性.

自动成图算法分为3个模块, 第1部分, 对厂站的位置进行布局, 为厂站找到合适的位置; 第2部分, 对厂站之间相连的线路采用A*算法进行线路规划. 最后一部分是将成图之后的结果进行评价反馈, 对于一些不合理的厂站和线路的布局不合理的进行微调, 通过局部微调适应整体布局.

输电网接线的成图算的目标是:

1) 厂站之间的相对空间的位置关系应该和实际的地理相对位置关系大致相似. 此目的是保证使用人员对输电网线路的位置上的使用习惯.

2) 整体布局均匀, 包括厂站和线路.

3) 厂站之间的连接线使用直线连接, 尽量采用横竖直线, 且拐点少.

4) 厂站线路的交叉尽可能少, 避免线路重合和拐点在线路上.

5) 主干线路(500 kV)以上的线路尽量布局在中心位置.

1 厂站网格布局 1.1 厂站网格布局的数学模型

厂站位置的布局是线路规划的基础和前提, 布局结果的优劣直接关系到线路规划的成图效果. 一个良好的厂站位置布局, 主要表现在厂站在画板上分布均匀、相邻之间的厂站的距离合理等几个方面.

厂站位置布局可以抽象成图当中的点, 输电线路抽象成图中的边, 节点和边就构成一个图模型. 因此厂站布局和输电线路规划就转换成点的布局和两点之间边的路径规划.

在大规模点的布局上, 力导向算法有着非常广泛的应用, 它的优点是可以清晰的展现图中各点之间的关系, 由Peter Eades在1984年首次提出^[4]. 该算法的核心是将图中的点和线模拟力学系统, 且图中的各点同时受到吸引力和排斥力的影响. 图中每个节点与其它节点都存在斥力, 有线连接的节点之间存在引力. 如果引力大于斥力, 则两个节点相互靠近; 如果斥力大于引力, 则两个节点相互拉远. 经过多次迭代, 最后形成一个稳定的系统. 具有代表性的力导向算法有Fruchterman TMJ等提出的基于原子引力模型的FR算法、Kamada T等提出的基于能量模型的KK算法和Hu YF提出的Hu氏算法^[5–7]. 本文采用FR算法, 它是在经典弹簧模型上的一些改进, 模拟物理粒子理论中原子之间的力场来调节位置关系.

在FR算法中, 需要计算以下几个值. 设定画布的宽为W, 高为H, 则画布大小为^[8]:

$S = W \cdot H$

(1)

理想距离:

$k = \sqrt {\frac{S}{{\left| {{V}} \right|}}} $

(2)

其中, $\left| {{V}} \right|$ 是节点的数量.

节点之间的欧式距离:

$d(u,v) = \sqrt {{{({u_x} - {v_x})}^2} + {{({u_y} - {v_y})}^2}} $

(3)

为了保证节点之间的距离稀疏合理, 需要计算节点之间引力和斥力. 然而斥力存在于所有节点之间, 而引力只存在于两个节点之间存在连线的情况, 这正好符号我们常规的理解, 有关联的节点之间的距离要近, 无关联的节点距离远. 所以有节点u和节点v之间的引力函数:

${f_a}(u,v) = \frac{{{{(d(u,v))}^2}}}{k} \cdot {F_1}$

(4)

节点u和节点v之间的斥力函数:

${f_r}(u,v) = \frac{{{{(d(u,v))}^2}}}{k} \cdot {F_2}$

(5)

其中, ${F_1}$ 和 ${F_2}$ 分别为引力因子和斥力因子.

厂站布局算法是基于FR算法为核心进行设计的, 在迭代过程中, 很容易出现局部优而整体差的情况. 为了避免这种情况, 本文选用模拟退火算法替代传统的迭代方式, 避免局部优化的情况. 模拟退火算法是模拟物理学上物体逐渐降温的物理过程, 温度越低, 能量越低; 最后达到相对稳定的状态.

线性温度下降表达式:

${T_{t + 1}} = \gamma \cdot {T_t}$

(6)

${T_t}$ 为当前时刻温度, ${T_{t{\rm{ + }}1}}$ 下一时刻温度, $\gamma $ 为冷却系数, 且一般为略小于1的正数.

本文设置初始温度为 ${T_0} = 1000$ , 停止温度为 ${T_{{\rm{end}}}} = 1$ .

为了选择最优的布点结果, 本文采用以下几个评价函数进行评价:

点的布局评价函数^[8]:

1) ${\text{边长偏差}}{\rm{ = }}\dfrac{{{\text{最长边长}} - {\text{最短边长}}}}{{{\text{平均边长}} \times {\text{图的边数}}}}$

2) ${\text{点分布偏差}}{\rm{ = }}\dfrac{{\dfrac{{\text{图的显示面积}}}{{\text{节点个数}}} - {\text{最小节点距离}}}}{{\text{图的显示面积}}}$

3) ${\text{代价}} = \left( {{\text{边长偏差}} + {\text{点分布偏差}}} \right) \times {\text{线路交叉数}}$

1.2 厂站网格布局的算法实现

FR算法的核心步骤主要分为3个部分, 首先计算图中各点之间的斥力, 其次计算有边相连的节点之间的引力, 最后计算斥力和引力的合力来计算节点的移动位置. 然而, 每一次计算只能得到图的部分能量最小, 要得到全局的能量最小, 需要经过多次迭代才能够满足需求.

在点的一定次数的位置偏移中, 随着迭代次数的增多, 位置的调整也越来越微小, 图形之间的布局会越来越好. 在模拟退火算法中, 给出初始温度和冷却速率来限制节点的最大位移. 随着温度的降低, 位置的偏移会越来越细微, 使得图最终能够得到一个相对稳定的状态. 在算法实现过程中, 为了得到较好的布点效果, 算法添加了并发的参数循环计算, 利用计算机多核CPU的计算性能, 计算出最优的参数值.

1.2.1 节点布局的伪代码

节点布局的伪代码如图1所示.

1.2.2 布点实验

不同的弹力系数 ${F_1}$ 和斥力系数 ${F_2}$ 对点的布局影响会非常的大, 故该算法通过多线程并行的计算不同 ${F_1}$ 、 ${F_2}$ 参数条件布点之后的相交代价, 通过比较, 选择最小代价的参数 ${F_1}$ 、 ${F_2}$ 和布局结果. 在实验中, 不同数据输入的情况中, 动态计算参数 ${F_1}$ 和 ${F_2}$ 的值比固定的 ${F_1}$ 和 ${F_2}$ 的值的效果要好很多.

实验中, 本文选取了57个厂站节点和98条边线路作为实验数据. 在CPU为Intel(R) Core(TM) i3-8130U CPU @ 2.20 GHz(2208 MHz), 内存为8 GB的单机笔记本电脑中对不同的冷却系数做了实验对比, 通过计算出的引力、斥力系数, 交叉偏差因子和运行时间评价布局结果的好坏.

通过表1数据结果可以看到, 当冷却系数为0.93时, 交叉偏差乘积最小, 运行时间最短. 而且通过实验发现, 布局效果不是随着冷却系数的增加而改变, 而是先增加后减小. 同时, 冷却系数对引力、斥力系数也有影响, 不同的冷却系数得到不同的引力、斥力.

对应图中的结果, 生成如图2所示的节点布局图.

图2中的6幅图分别展示了49个节点和连线的分布情况. 从图中看出, 从 $\gamma {\rm{ = 0}}{\rm{.92}}$ 开始, 点的布局就变的扁长, 点的布局也较为稀疏. 单具体才差别并不大. 但从表1的测试结果数据中可以知道, 当 $\gamma {\rm{ = 0}}{\rm{.93}}$ 时, 效果最好.

2 输电线路规划

厂站规划的位置布局完成后的线路规划直接决定着图形的美观程度. 如果线路像图1那样采用直连, 则会产生非常多的交叉且不美观. 线路增多时, 交叉更是会指数性增多. 故需要一种高效率的全局的线路规划算法, 实现线路的美观布局. 常见的线路规划算法有Dijkstra算法^[9]、Bellman - ford算法^[10]、Floyd-Warshall算法^[11]、SPFA算法^[12]、李氏迷宫算法^[13]和A*搜索算法^[14]这几种算法. 本文采用的A*算法是一种启发式式搜索算法, 是求解最短路径中最有效的算法. 它具有算法灵活, 效率高等优点.

2.1 目标

经过第一步节点布局的基础上, 得到密度合理的节点分布, 线路规划的目标有以下几个方面:

1) 线路交叉和拐点尽量少, 且拐点尽量不在线上;

2) 线路尽量横平竖直, 出线和入线为0°、30°、45°、60°和90°;

3) 线路之间重合线尽量少, 出线和入线重合除外;

4) 所有节点必须在网格点上.

通过上面的要求和目标, 本文设计了下面的代价模型.

2.2 代价函数模型

在A*算法中, 代价函数g(x)和h(x)决定线路的走向. 而h(x)作为启发函数, 其作用是控制A*算法的行为, 引导A*算法快速接近目标节点. g(x)在A*算法中对路径规划起主要作用, 它决定两点之间中间的路径该如何规划.

下面为起点到节点i的最小代价函数 ${t_i}$ :

${t_i}{\rm{ = }}{t_{i - 1}} + \min ({\omega _1}{f_1} + {\omega _2}{f_2} + {\omega _3}{f_3} + {\omega _4}{f_4}) = \sum\limits_{k = 0}^i {{g_k}(x)} $

(7)

${t_{i{\rm{ - }}1}}$ 表示起点到当前节点的最小代价, 则 ${t_{\rm end}}$ 表示到从起点到终点的代价值, 其中 $\min ({\omega _1}{f_1} + {\omega _2}{f_2} + {\omega _3}{f_3} +$ $ {\omega _4}{f_4}) $ 为当前节点到下一节点的 $g(x)$ 最小代价. ${\omega _1}{\text{、}}{\omega _2}{\text{、}} $ ${\omega _3}{\text{、}}{\omega _4}$ 为权重系数, ${f_1}$ 为线路交叉函数; ${f_2}$ 为线路拐角函数; ${f_3}$ 为区域影响函数; ${f_4}$ 为路径长度函数.

那么在线路规划中, 所有线路(重复线路值算一条)的总代价值就为:

${{T = }}\sum\limits_{i{\rm{ = }}0}^n {{t_{{\rm end}(i)}}} $

(8)

1) 线路交叉函数

${f_1}{\rm{ = }}{a_1}m + {b_1}n + {c_1}({b_1} > {a_1})$

(9)

输电线路分为不同的电压等级, 若当前线路与其它线路的相交且电压等级相同, 用n表示不同电压等级的条数, m表示相同电压等级的条数, ${a_1}$ 和 ${b_1}$ 表示不同电压等级的权重. 通过 ${b_1}$ > ${a_1}$ 的条件限制使得在线路规划中, 尽量避免相同电压等级的线路的交叉, 而选择不通电压等级线路交叉的情况. ${c_1}$ 是常数影响因子, 它的主要作用是调整 ${f_1}$ 函数的权重大小.

2) 线路拐角函数

针对不同的线路出线情况, 设定不同的权重值.

若该线为出线, 则 ${f_2}{\rm{ = }}0$ ; 若为后面的几种情况, 则是不同的权重值, 在不同的情况下, 选择不同的走向. 并且在线路规划中, 为了美观, 更倾向于横平竖直, 且拐弯少的情况. 故在以下6种情况下, ${a_2}$ 这种情况最好且 ${a_2}$ 的值最小; 其它几个权重值则需要根据不同的线路规划需要设定不同的值.

3) 区域影响函数

设起点为P, 终点为Q, 中间某一节点的E, 区域影响函数为:

${f_3} = {a_3} \cdot F(P,E) + {b_3}F(Q,E) + {c_3},\;\;{a_3} > {b_3}$

其中, $F(P,Q)$ 为P, Q连接函数. 要求 $F(P,Q)$ 的值, 首先要得到除当前连接的厂站外, 其它与P有连接的变电站; 第二步, 假设其中的一个变电站的坐标为 $p(x,y)$ , $P({x_{p}},{y_p})$ , $Q({x_q},{y_q})$ .

$F(P,Q){\rm{ = }}\left\{ {\begin{array}{*{20}{c}} 1,&\begin{gathered} \min ({x_p},{x_q}) \le x \le \max ({x_p},{x_q})\;{\rm or} \\ \min ({y_p},{y_q}) \le x \le \max ({y_p},{y_q}) \\ \end{gathered} \\ 0,&{{\rm{otherwise}}} \end{array}} \right.$

(12)

图3是经过E点时, $F(P,E) = 1$ , $F(Q,E) = 1$ ; 同样在经过 ${E_{21}}$ 时, $F(P,{E_{21}}) = 1$ , $F(Q,{E_{21}}) = 1$ ; 而 $F(P,{E_{12}}) = 0$ , $F(Q,{E_{12}}) = 1$ ; 故此时会选择 $P \to {E_{12}} \to Q$ 这条路径. 此外, ${a_3} > {b_3}$ 的作用是规范路径出线的方向, 当一个点的出线较多时, 对其它的线路影响相对较小一些.

4) 路径长度函数

路径函数的作用是记录线路的路径长度, 可以减少线路之间不必要的步数. 当两条线路起点终点一致的情况下, 优先选择路径长度 ${f_4}$ 最小的情况. 其中 ${{{a}}_4}$ 为路径函数的权重系数.

${f_4}{\rm{ = }}{{{a}}_4} \cdot d$

(13)

2.3 路径规划算法

路径规划A*算法的核心是如何计算代价函数, 它决定了从起点到终点每一个中间节点的位置. 它的代价函数为:

$f(x) = h(x) + g(x)$

(14)

其中, $g(x)$ 是起点到中间某一节点的最短距离; $h(x)$ 为启发函数, 一般取曼哈顿距离^[15], 切比雪夫距离^[16]、欧几里得距离或平方后的欧几里得距离为主要函数. 如果 $h(x){\rm{ = }}0$ , 则A*算法退化为Dijkstra算法. 根据2.2可知, $g(x){\rm{ = }}{{{t}}_i}$ . 同时设定启发函数切比雪夫距离, 即为 $h(x){{ = D}} \cdot \max (\left| {{x_1} - x} \right|,\left| {{y_1} - y} \right|)$ . 基于A*算法, 结合上面的数学模型, 最终得到厂站的线路规划算法.

2.3.1 数据预处理

1) 线路去重

因为输电线路中有大量的起点终点变电站一致的情况. 如“代东I线”和“代东II线”, 这两条输电线路的起点变电站和终点变电站都为代王变和东郊变. 在后面的路径规划中, 因为要涉及到线路交叉和重复计算的情况, 所以, 要在路径规划前, 先去除重复的线路. 之后在显示线路时, 在通过节点偏移算法将重复的线路按照相对位置进行偏移.

2) 线路排序

按照线路的电压等级和线路长度两个参数进行排序. 优先按照电压等级由高到低, 其次是按照线路的长度由短到长进行排序. 按照习惯, 电压等级高的线路作为核心线路, 要求为横平竖直, 交叉和拐角少, 所以优先对其进行排序. 第二按照线路由短到长进行排序, 目的是优先安排短的线路, 短的线路相比长的线路更容易布置且不会有太多的拐角. 实验过程中发现, 不同排序顺序的成图效果会非常大.

3) 剔除T接线

T接线是输电线路中比较特殊的情况, 它的一端直接连接到一条主干线路上. 而普通的线路时连接着两端厂站, 这种情况直接进行线路规划; 而对T接线则需要重新计算T接点的位置后在进行线路规划. 故需要对其剔除特殊处理.

2.3.2 路径规划算法描述

第1步. 单线路路径规划.

(1) 依次处理预先已排序的线路, 优先对高电压等级的线路进行布线. 设定电压门槛值, 若高于此值, 则出线方向为上下左右及各个方向的45度角等8个方向; 否则出线方向增加30度和60度等16个方向. 此为第一步出线.

(2) 使用A*算法实现从起点到终点的线路规划, 得到路径的中间拐点.

第2步. T节线处理.

因为T接线是一种特殊的线路, 它的一端是主线路的一个T接点, 另一端是厂站. 所以在线路规划中, 首先需要在主线路上找一个合适的点作为T接点, 本文算法是在主线路中最长线段的等分点, 如有一个T接点, 则为二等分点处. 之后在按照第一步的算法进行线路规划.

第3步. 重复路径偏移.

(1) 将重复的线路分组.

(2) 将每条线路的中间节点进行优化, 若连续的3个点在一条直线上, 则去除中间点. 此过程是减少线路中的多余节点. 若中间节点太多, 则加入反馈列表, 对厂站布局进行反馈.

(3) 对重复的线路按照某种特定的规则进行偏移. 本文实验中采用每两条线相隔4个单位.

(4) 最后输出线路及中间拐点.

2.4 路径规划算法样例

图4为使用A*路径规划算法, 结合代价函数模型的路径节点的代价图. 图中的数字为起点A为到终点B中间所计算的各个节点的最小代价. 其中从点A到点B的最小代价为10, 在图中为灰色有背景部分. 直观上看, 符合成图的最终需求.

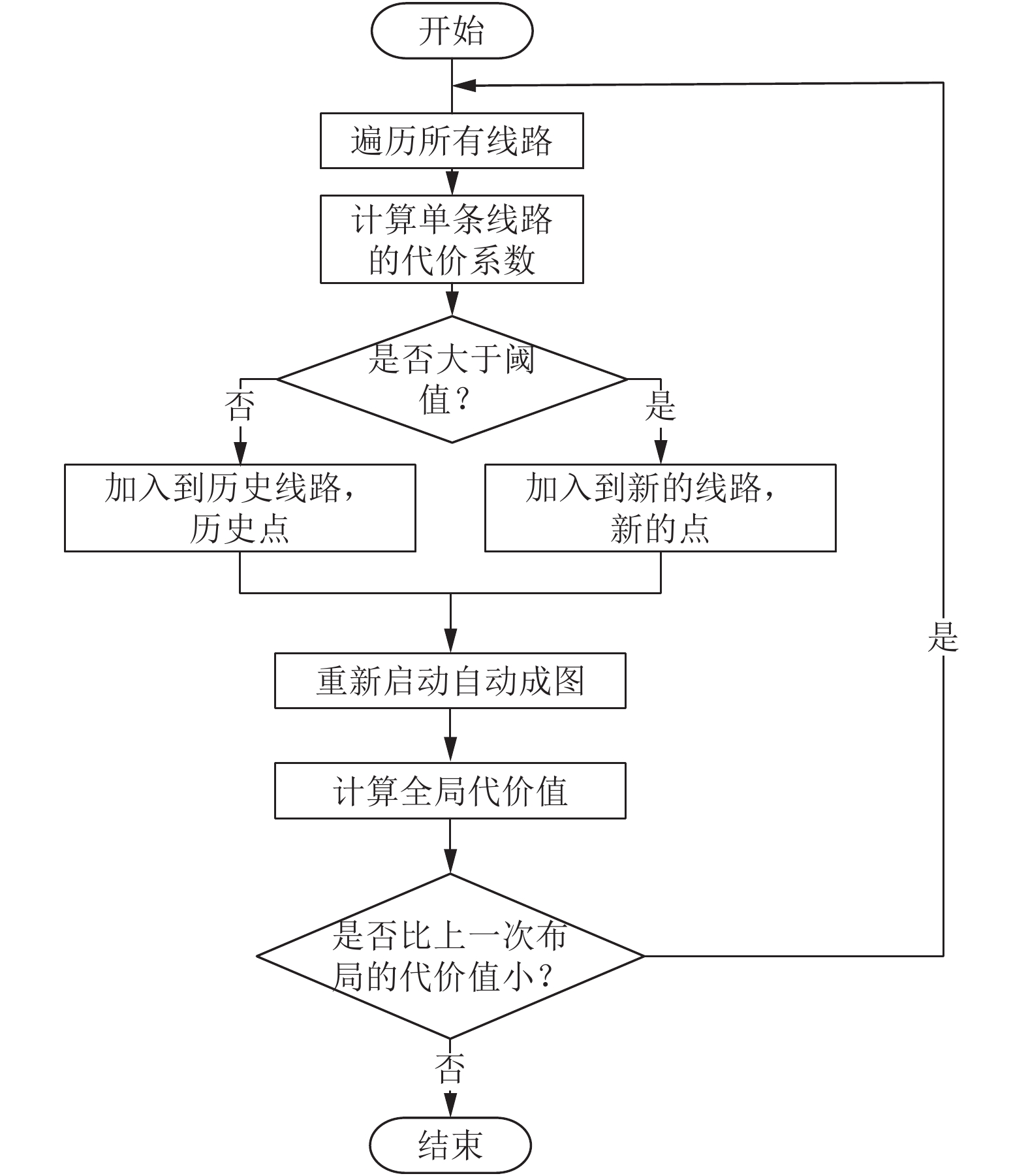
3 线路规划反馈厂站布局

在线路规划过程中点是固定的, 所以一定会产生点布局不合理而导致线路规划不美观的情况, 因此需要对已经规划好的线路, 进行点的位置的调整. 本文所采取的策略为增加反馈环节, 多次对点进行反馈微调来达到目标的美观效果. 图5为线路规划反馈算法的流程图.

通过遍历已经成好的图的每条边, 设定反馈阈值. 若某条线的代价超过设定的阈值, 就将线和两端端点以及端点所关联的线, 加入到需要重新布线和布点数组中. 而不被改变的线路和点则设置为历史的线路和点, 重新布线的线和点则设置为新的线路和点. 在经过厂站布局和线路规划后, 计算其总代价, 与上一次布局代价相比较, 选择较小的布局结果. 当布局结果的代价不在减小时, 此时, 停止反馈, 输出布局结果.

而本文设定的反馈阈值L为所有线路规划前10%的代价值, 换句话说, 就是每次对至少10%的线路进行微调.

选取42个点和68条线进行实验. 经过初始布局和三次迭代之后, 输出结果. 在反馈过程中, 布局总代价逐渐减少, 点布局和线规划都存在位置的改变和优化, 成图效果不断改善. 图6为不同迭代时期的代价及成图效果.

4 增量厂站线路规划

随着输电线路的不断建设, 厂站线路投运和退役是比较常见的事. 所以在厂站线路布局完初始布局完以后, 有新的厂站线路投运再次布局时, 就需要不改变原来的线路和厂站位置, 只调整和布局相关的厂站和线路即可. 为了满足这个需求, 只需在厂站布局和线路规划算法做一些预处理和微调即可.

1) 数据预处理

传入的厂站和线路分为历史厂站、历史线路和新建厂站和新建线路. 若新建线路的两端厂站在历史线路中能找到相同起始和终点厂站, 则将与其相同的线路的中间节点复制到这条线路中, 同时将其节点移除新建线路, 加入到历史节点中.

同时设置所有线路和所有厂站两个变量, 供厂站布局使用.

2) 厂站布局

在所有处理逻辑不变的情况下, 只改变循环变量. 新建厂站在计算排斥力时, 只计算新建厂站与其它所有厂站之间的斥力; 计算引力时, 只计算该场站与其它相关联的厂站的引力. 这样对历史厂站的位置不会产生影响, 只需布置新的厂站的位置.

3) 线路规划

线路规划也只需将循环变量改为新建线路; 只规划新建线路的中间节点的路径.

图7为增量布局的结果. 图7(a)为原始的厂站布局, 图7(b)在原始厂站都没有改变的情况下新增了2个厂站和3条线路. 其中1条为普通线路, 另外2条为T接线路. 而且通过增量成图算法找到的位置从实际效果上也比较合理, 基本符合增量成图目标效果.

5 评价及实验结果

该算法的有两个核心模块组成, 点布局力导向算法的一次迭代的时间复杂度为O(|V²||E|), 经过模拟退火迭代的时间复杂度为O(n•|V²||E|). 表2为计算不同冷却系数下的代价和运行时间, 很明显, 当冷却系数为0.92时, 总代价最小, 且运行时间最短. 图8是不同的冷却系数生成的实验结果, 可以看到成图结果基本满足美观的要求. 且在 $\gamma {\rm{ = 0}}{\rm{.92}}$ 时, 效果最好.

6 结语

本文通过实现改进力导向算法和A*算法, 构建了一个线路规划的模型函数及评价函数, 并通过布点, 布线, 反馈三个步骤, 实现了输电线路增量自动成图的功能. 同时还对影响成图的参数进行了实验比对, 得到了当 $\gamma {\rm{ = 0}}{\rm{.92}}$ 或者 $\gamma {\rm{ = 0}}{\rm{.93}}$ 时成图效果较好. 由于成图的时间复杂度高, 存在当数据量较大时, 成图时间较长的问题. 下一步需要深入研究, 解决这方面问题.