作为传统聚类算法模糊C-均值聚类算法(Fuzzy C- Mean clustering algorithm, FCM)的一种优化算法, 引入了粒子群优化算法(Particle Swam Optimization, PSO), 粒子群模糊聚类算法(Particle Swarm-based Fuzzy Clustering algorithms, PSO-FCM), 通过PSO算法的收敛速度快, 粒子收敛由自身最优位置和群体最优位置相结合, 在一定程度上解决了FCM对初始值敏感, 对噪声数据敏感, 容易陷入局部最优解的缺点. 如今, 随着数据量多样化, 复杂化, 多类别化, PSO-FCM只是单一优化初始聚类中心选取问题, 没有合理的限制粒子的移动, 并不能更好优化好FCM算法面对多聚类问题时^[1–7].

为了解决上述问题, 引入主成分分析(Principal Component Analysis, PCA), 本文提出基于PCA优化的粒子群模糊聚类算法(PCA-PSO-FCM), 通过PCA对数据各维度的分析和评定综合给出一个权重值, 粒子各维度会根据该调整权重速度和方向. 本文详细介绍了PCA-PSO-FCM, 并且与FCM和PSO-FCM进行了实验结果的比对, 从实验上来看, 本文的算法在多种群聚类问题上性能更好, 是一种很有潜力的聚类算法.

本文结构如下: 第1部分主要对已有的算法的研究成果进行简要分析总结; 第2部分对于本文的优化算法进行详细说明; 第3部分说明实验过程相关细节, 设定参数以及实验结果的分析; 第4部分总结全文.

1 算法介绍

PSO-FCM算法是模糊均值聚类算法基础上的优化算法, 传统的模糊C均值算法的结果精度, 对初始中心的选取有很严格的要求, 并且容易陷入局部最优解. 为了解决这个问题, 国内许多学者, 利用具有集体智能的粒子群优化算法, 与传统模糊C均值算法结合. 利用PSO算法求解初始聚类中心, 进而优化了FCM依赖初始中心的问题; 利用PSO算法中, 粒子个体与粒子群体之间关系, 粒子整体移动的速度可以调节, 进而降低了FCM容易陷入最优解的可能性.

1.1 PSO-FCM算法

PSO-FCM算法是基于数据样本之间的模隶属矩阵建立的聚类算法. 算法的核心思想是: n个文本样本为 $X = ({x_1},{x_2},\cdots,{x_n})$ , 划分为 ${\rm{C}} = ({c_1},{c_2},\cdots,{c_n})$ , p个聚类中心, 计算出每个文本的隶属度 ${\mu _{ij}}$ , ${\mu _{ij}}$ 表示第j个样本隶属于第i个样本的隶属度.

$\sum\nolimits_{i = 1}^p {{\mu _{ij}}} = 1,{\mu _{ij}} \in \left[ {0,1} \right]$

(1)

${\mu _{ij}} = \left\{ {\begin{aligned} &{1/\sum\nolimits_{k = 1}^p {{{\left( {{d_{ij}}/{d_{kj}}} \right)}^{\tfrac{2}{{m - 1}}}}} }{,\;{d_{kj}} \ne 0}\\ &0{,\;\;\;{d_{kj}} = 0} \end{aligned}} \right.$

(2)

根据每个样本的隶属度值计算出适应度函数值:

${J_m} = \sum\nolimits_{j = 1}^n {\sum\nolimits_{i = 1}^p {{{({\mu _{ij}})}^m}{{({x_j} - {c_i})}^2}} } $

(3)

${c_i} = \frac{{\displaystyle \sum\nolimits_{j = 1}^n {{{({\mu _{ij}})}^m}{x_j}} }}{{\displaystyle \sum\nolimits_{j = 1}^n {{{({\mu _{ij}})}^m}} }}$

(4)

$\nu _i^{k + 1} = \left\{ {\begin{array}{*{20}{l}} {\varpi \nu _i^k + {c_1}{r_1}({\rho _i} - x_i^k) + {c_2}{r_2}({\sigma _i} - x_i^k)}{,\;\;k > 1} \\ {{c_2}{r_2}({\sigma _i} - x_i^k)}{,\;\;\;k = 1} \end{array}} \right.$

(5)

$x_i^{k + 1} = x_i^k + \nu _i^{k + 1}$

(6)

式中, m是加权指标, $m > 1$ , ${x_j} - {\nu _i}$ 表示样本 ${x_j}$ 到第i个样本中心的聚类, PSO-FCM算法适应度函数 ${J_m}$ 值越小说明性能越好; $\;{\rho _i}$ 是粒子最优适应度的位置, ${\sigma _i}$ 是群体最优适应度函数, ${c_1}$ 和 ${c_2}$ 是学习因子; ${r_1}$ 和 ${r_2}$ 是[0,1]之间的随机因子数, $\varpi $ 是惯性权重.

2 算法优化 2.1 PCA算法

随着数据量的爆发和激增, 数据类型的增多, 数据复杂程度的加深, PSO-FCM算法的性能无法完全发挥. 于是近年来有学者对该算法进行了再度优化, 陈寿文^[8]提出利用混沌粒子融合粒子群模糊聚类算法(CCPSOFCM), 余晓东等^[9]利用直觉模糊核优化粒子群模糊聚类算法. 雷浩辖等^[10]利用遗传算法(GA)与PSO混合优化的遗传粒子群模糊聚类(GA-PSO-FCM). 这些学者都是针对于PSO-FCM算法依赖初始解这个问题上进行的优化. 算法核心是通过比较隶属度, 移动该粒子并决定属于哪一类, 但是在各维度上面的移动上并没有一个主次之分, 在各维度上的移动全部是随机因子数决定. 随着聚类中心数量的增加, 隶属度矩阵上, 各聚类中心隶属度值接近, 粒子各维度移动不受限, 这样导致部分粒子可能会被分入, 与正确聚类中心隶属度值接近的错误聚类中心中的问题. 在维度增加, 聚类中数量增加, 这个问题会越来越频繁出现.

为了在一定程度降低上面的问题出现的可能性, 本文引入了PCA^[11–13]算法对原算法进行优化, PCA是一种统计分析的方法, 通过正交变换将具有一定相关性的向量转为彼此正交, 且互相独立的一维新向量(即主成分). 每个主成分都是初始变量的线性组合, 没有冗余信息, 构成空间的正交基. 主成分分析法可以简化统计数据, 揭示特征变量之间的关系. 在本文优化中并没直接对数据进行降维, 根据PCA中主成分贡献率公式: ${\eta _k} = \dfrac{{{x_k}}}{{\displaystyle \sum\nolimits_{i = 1}^m {{x_i}} }}$ , 计算出样本空间各维度之间的贡献率 $\eta = ({\eta _1},{\eta _2},\cdots,{\eta _n})$ , 进一步优化PSO-FCM算法中速度的 $\nu _i^{k + 1}$ 的迭代公式:

$\left\{ \begin{aligned} & {\gamma _1} = {\eta _1}{r_1}, \;{\gamma _2} = {\eta _2}{r_2}\\ &\nu _i^{k + 1} = \left\{ {\begin{array}{*{20}{l}} {\varpi \nu _i^k + {c_1}{\gamma _1}({\rho _i} - x_i^k) + {c_2}{\gamma _2}({\sigma _i} - x_i^k)}{,\;\;k > 1} \\ {{c_2}{r_2}({\sigma _i} - x_i^k)}{,\;\;\;k = 1} \end{array}} \right. \end{aligned}\right. $

(7)

2.2 优化算法实现

输入: 短文本数据集 $X = ({x_1},{x_2},\cdots,{x_n})$

初始化: 加权指标m; 学习因子 ${c_1}$ 和 ${c_2}$ ; 惯性权重 $\scriptstyle \varpi $ ; 训练轮数T.

随机初始化: 初始聚类中心 $\scriptstyle C_0 = \left(c_1^{(0)},c_2^{(0)},\cdots,c_p^{(0)}\right)$

1. $\scriptstyle {C^{\rm best}} \leftarrow {C_0}$

2. $\scriptstyle J_m^{(0)} \leftarrow {\sum\nolimits_{j = 1}^n {\sum\nolimits_{i = 1}^p {{{({\mu _{ij}})}^m}\left({x_j} - c_i^{(0)}\right)} } ^2}$

3. $\scriptstyle J_m^{\rm best} \leftarrow J_m^{(0)}$

4. for $\scriptstyle t = 1,2,\cdots,T$ do

5. 　 $\scriptstyle {\rho _{\rm best}} \leftarrow x_i^t$

6. 　 $\scriptstyle pindex \leftarrow \arg \max ({\mu _{ij}},j = 1,2,\cdots,p)$

7. 　 $\scriptstyle {\sigma _{\rm best}} \leftarrow c_{ pindex}^{(0)}$

8. 　for $\scriptstyle i = 1,2,\cdots,I$ do

9. 　　 $\scriptstyle \nu _i^{t + 1} \leftarrow {c_2}{\gamma _2}({\sigma _2} - x_i^t)$

10. 　　 $\scriptstyle x_i^{t + 1} \leftarrow x_i^t + \nu _i^{t + 1}$

11. 　　if $\scriptstyle J_m^{\rm best} > J_m^{(t)}$ then

12. 　　　 $\scriptstyle J_m^{\rm best} \leftarrow J_m^{(t)}$

13. 　　 $\scriptstyle {J_m} = \sum\nolimits_{j = 1}^n {\sum\nolimits_{i = 1}^p {{{({\mu _{ij}})}^m}{{({x_j} - {c_i})}^2}} } $

14. 　　 $\scriptstyle {C^{\rm best}} = \frac{{\sum\nolimits_{j = 1}^n {{{({\mu _{ij}})}^m}{x_j}} }}{{\sum\nolimits_{j = 1}^n {{{({\mu _{ij}})}^m}} }}$

15. 　　else continue

16. end for

17. 输出中心 $\scriptstyle {C^{\rm best}}$ , $\scriptstyle J_m^{\rm best}$

3 实验分析 3.1 实验数据处理

在测试算法的性能, 本文选择UCI机器学习数据库中, Wine, Breast Tissue, Dermatology, 以及Glass Identification, 每一组数据都进行了清洗, 并且都做了使用线性函数归一化将数据集进行标准化处理. 各维度的权重是通过主成分分析得出各维度贡献率, 数据集参见表1 数据集表.

3.2 模型评价指标

通过对比本算法与K-近邻(KNN), FCM, PSO-FCM在数据集训练的结果. 本文采取的评价算法性能的指标: 调整互信息(Adjusted Mutual Information based scores, AMI); 调整兰德系数(Adjusted Rand Index, ARI); FM指数(Fowlkes and Mallows Index, FMI). 3个指标都是评价聚类算法性能的外部指标, 通过聚类结果与参考数据集的标签比较而获得, 这些外部指标度量的结果都在[0, 1]之间, 指标值越接近1说明聚类的结果越好.

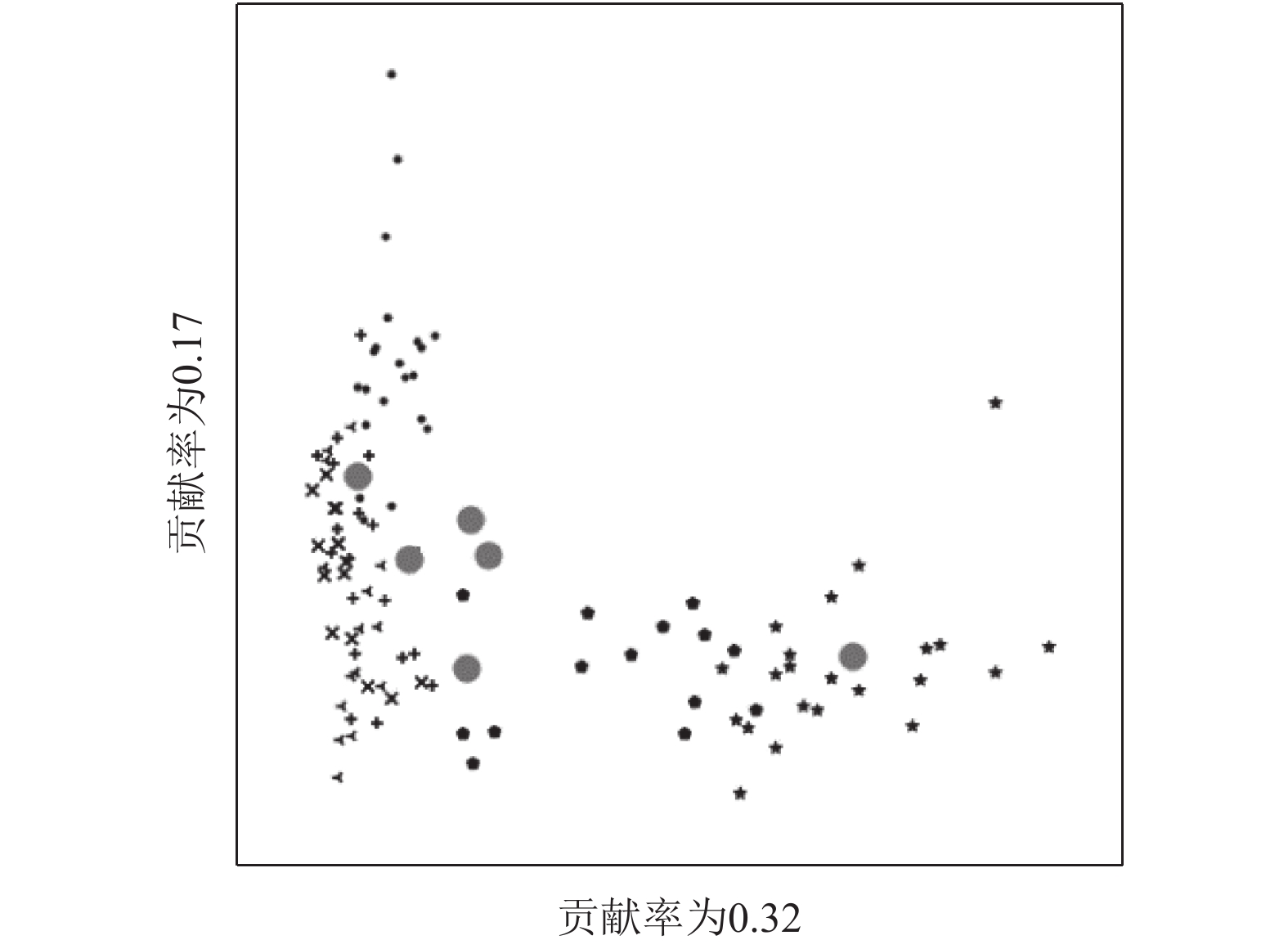
3.3 检验模型性能

图1和图2根据Breast Tissue数据集的主成分贡献率所选择的平面图, 图1是本文算法在数据集上, 两个高贡献率维度的图像, 图2是PSO-FCM算法, 从图中可以明显的对比出来, 在相同数据集, 相同维度下的本文算法聚类的结果明显优于PSO-FCM, PSO-FCM算法在数据比较集中的区域, 对于多个聚类中心的交界处的数据敏感程度低, 无法有效的给出数据的准确的聚类中心, 相反本文算法面对这类粒子, 敏感度高, 能够更加有效的且准确的给出聚类中心. 粒子各维度之间无差别移动, 在多个聚类中心的粒子会被错误的移动到不正确的聚类中心中: 本算法对于不同贡献率的空间中, 采取相对应的移动权重的能够较低粒子错误移动的概率, 说明该策略效果是显著的.

由表2和表3中可以看出, 本文算法只是在Dermatology数据集上的AMI这一个指标上落后KNN, 这是因为作为硬聚类算法, 随着聚类中心数目的增加, 每一个数据只能存在单一的一个聚类结果, 不会存在多种可能性, 聚类的结果纯度更高. KNN算法性能很稳定, 在随着聚类中心增多, 性能反超FCM, PSO-FCM两个算法, 但是综合指标上, 本文的算法总体仍是优于FCM, PSO-FCM, KNN这3个算法. FCM采用随机初始的中心, 指标随着聚类中心的增多, 算法性能下降明显. PSO-FCM采取使用PSO算法得出的初始中心, 明显的发现, 综合性能上面性能上优于FCM, 但是算法精度提升不高.

随着各数据集的聚类中心的增加, 聚类的问题的复杂化, 从表中各指标上, 侧面体现本算法面对多个聚类中心的之间的粒子敏感度更高, 分辨能力更强. 总体上指标上来看, 本文算法性能更强, 鲁棒性更高, 适用面更广.

4 结论与展望

采取PCA优化的PSO-FCM算法, 通过主贡献率加权的限制, 控制粒子各维度上的移动, 降低多聚类群交界粒子的敏感性, 增强了粒子的搜索能力, 降低粒子被不正确粒子群吸入, 能够一定程度上, 跳出局部最优, 有效的弥补了传统PSO-FCM性能上的不足, 增加算法精度, 增强算法的鲁棒性, 相对于其他算法, 在综合指标上面更优, 部分指标上有着更好的精度, 适用面更广, 鲁棒性更强. 接下来的工作会将优化算法应用到更多领域.