2. 数字福建环境监测物联网实验室, 福州 350117;
3. 福建省光电传感应用工程技术研究中心, 福州 350007
2. Digital Fujian Environmental Monitoring IoT Laboratory, Fuzhou 350117, China;
3. Fujian Provincial Engineering Technology Research Center of Photoelectric Sensing Application, Fuzhou 350007, China
电梯, 已逐渐成为城市生活的基础设施, 是现代人类出行活动最后50米的重要交通工具[1]. 随着我国城市化进程的发展, 电梯保有量、年产量、年增量均为世界第一[2]. 与其他发达国家相比, 我国电梯使用呈现负载高、运量大、随机性强等特点, 电梯事故时有发生[3]. 近十年来, 通过信息技术手段如物联网对电梯运行等安全性监测, 使得电梯事故率持续下降[4].
随着电梯安全性能提升的同时, 电梯舒适性也渐渐成为人们乘梯、用梯的关注重点. 考虑到电梯轿厢异常震动是电梯安全性能的关键, 也是电梯乘坐舒适度的关键指标之一, 为此, 2016年姚长鸿等通过振动传感器来采集异常震动, 将震动的突变嵌入到安全管理[5], 给电梯的安全管理注入的新观点. 顾雯雯等[6]从乘客的视觉角度及电梯的运行性能两方面着手, 重点分析了影响电梯乘坐舒适感的主要原因与影响因素. 宋涵通过电梯的装潢、结构、速度控制方式构建了基于AHP模糊综合评价法对电梯的舒适性进行评估的体系[7], 通过分析得出各个因素对影响电梯舒适性的程度. 这些研究从电梯的构成、装饰等方面尝试对电梯的安全性和舒适性进行了初步研究.
这些年, MEMS (Micro Electro Mechanical System)技术呈现体积小、灵敏度高、维度多等发展趋势[8], 已广泛应用于汽车工业、地质灾害以及航空航天等众多领域. 九轴传感器就是MEMS技术发展的典型代表, 它采集加速度、磁场和角速度等多维度数据, 为深化行业应用提供了多维数据视角. 王贇贇等应用九轴传感器采集汽车的数据, 通过互补滤波实现误差补偿, 再使用四元数法进行姿态解算, 得到汽车的姿态角, 进一步研究了汽车运动姿态和安全行驶之间的相关性[9]. Shi G等使用九轴传感器采集汽车的数据, 利用传统的线性卡尔曼滤波实现四元数的姿态解算并提出了新的方法来单独新更磁力计, 消除了对姿态估计的影响[10]. 刘飞飞等应用九轴传感器采集危岩的数据, 经内置运动处理引擎(DMP)处理得到危石四元数后, 解算出危岩危石的姿态角, 来监测其滚动和震动的情况[11]. 张煌军等通过应用九轴传感器采集无人机数据, 将加速计和磁力计的数据通过平方根容积卡尔曼滤波来纠正陀螺仪误差, 再用四元数进行姿态解算, 从而提高无人机飞行姿态解算的精度[12].
电梯作为在有限空间内导轨上运行的特种设备, 其姿态、加速度、速度等直接影响乘梯用梯的舒适性以及安全性等体验, 因此, 将九轴MEMS传感器应用于电梯监测领域中, 解算获得电梯姿态, 无疑有助于开展电梯的安全性评估和舒适性分析, 是一项具有重大意义的研究.
2 数据采集设计 2.1 硬件设计九轴MEMS数据采集电路图如图1所示, 传感器内部包含了三轴加速计、三轴陀螺仪、三轴磁力计, 可以采集加速度、角速度、磁场的数据, RX和TX分别为传感器的UART接收端和UART发送端, 与嵌入式微处理器进行数据交互, 由嵌入式微处理器对接收到的数据进行计算分析、完成姿态解算后进行持久化存储.
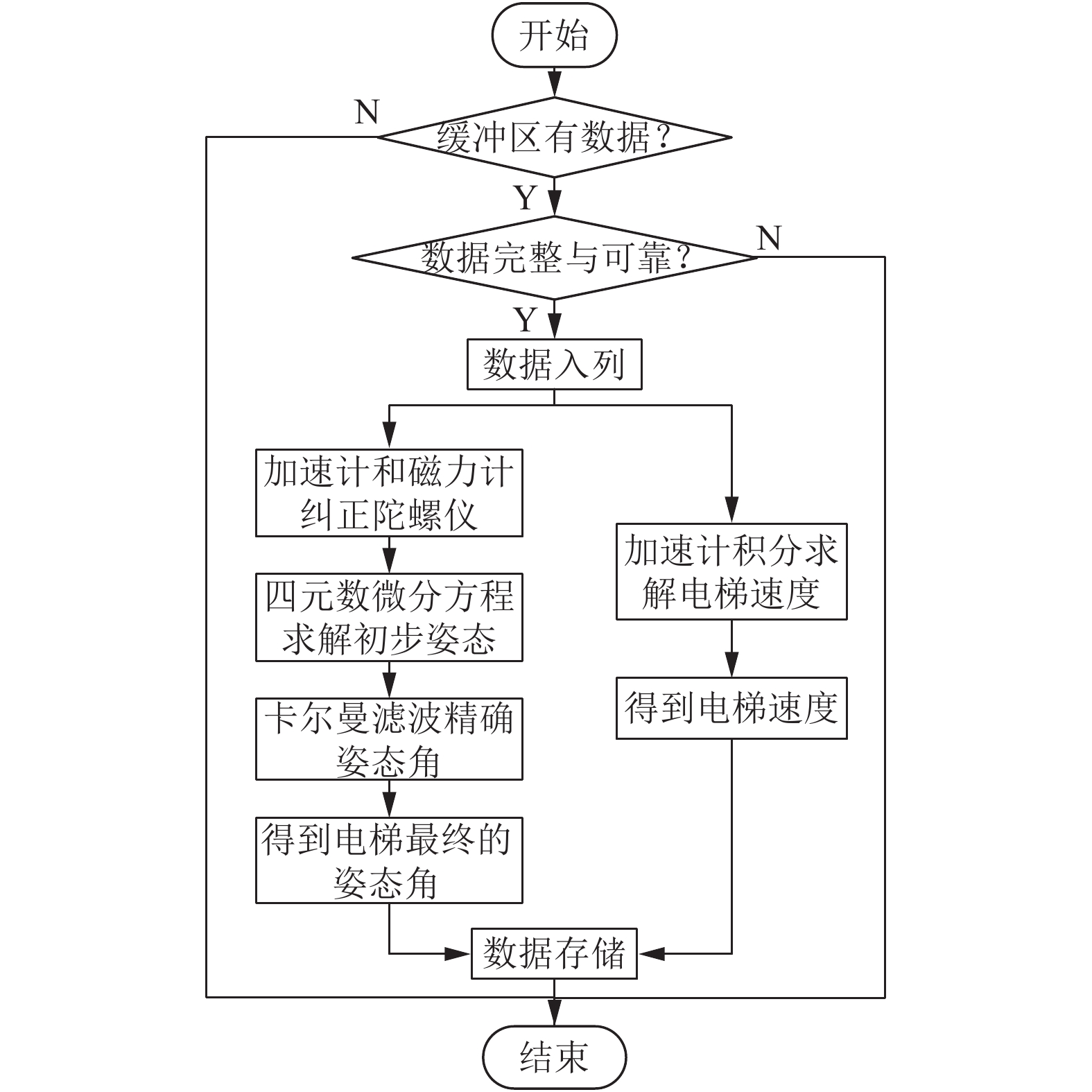
2.2 软件设计嵌入式软件的流程图如图2所示. 总体方案是: 通过定时器接收传感器发送的数据. 首先, 对数据进行完整性和可靠性校验, 以队列的方式存储校验通过的数据, 然后进行电梯运行姿态和状态的计算. 将采集到的加速计和磁力计数据利用互补滤波纠正陀螺仪数据通过四元数微分方程进行姿态角初步求解, 最后卡尔曼滤波对初步求解的姿态角进行数据精确化, 得到最终的姿态角. 同时, 利用加速度对时间进行积分得到电梯的运行姿态. 最后进行持久化存储, 方便数据的整理分析.

|
图 1 九轴MEMS数据采集电路图 |
|
图 2 软件设计流程图 |
3 数据处理 3.1 四元数姿态解算
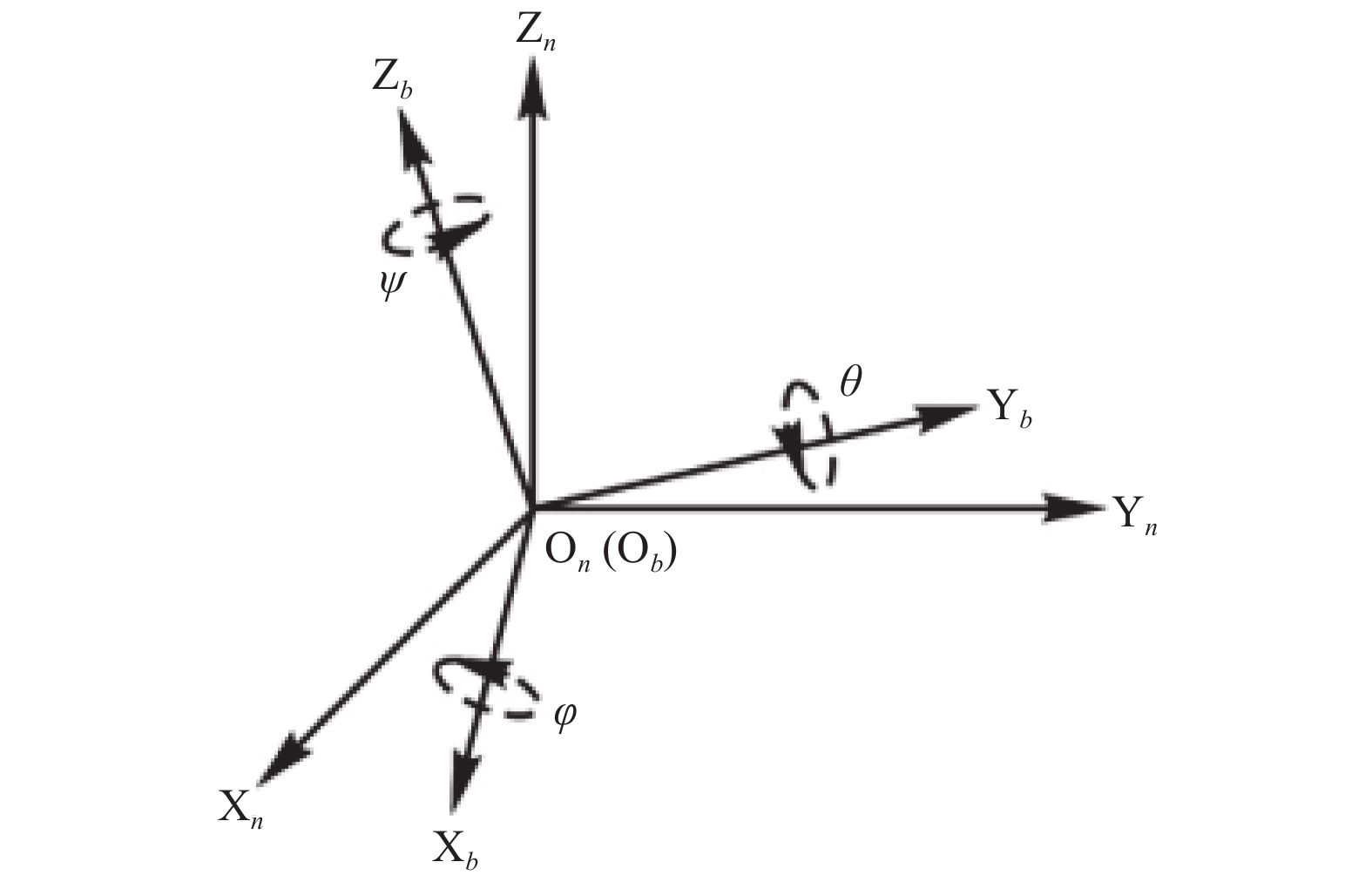
通常, 通过引入导航坐标系(简称n系, 由Zn、Xn、Yn组成)和载体坐标系(简称b系, 由Zb、Xb、Yb组成)来描述姿态, 如图3所示. b系可以由n系绕Xn轴、Yn轴、Zn轴转动表示, 其中旋转的角分别是俯仰角φ、横滚角θ、航向角ψ, 它们统称为欧拉角或姿态角[13].
|
图 3 姿态角表示图 |
求解姿态角方法有欧拉角法、方向余弦法、四元数法[14], 其中, 欧拉角法存在奇异点现象无法表示物体的全姿态, 方向余弦法则存在计算量大和解算复杂度高的问题[15], 而四元数法具有计算量小、无奇异点现象等优点, 因此, 主要通过对陀螺仪数据用四元数法求解姿态[16]. 捷联惯导系统理论定义了四元数q[17]:
| $ q = q_0 + q_1 i + q_2 j + q_3 k = {[ q_0 , q_1 , q_2 , q_3 ]}^{\rm T} $ | (1) |
q0为四元数标量部分, q1、q2、q3为四元数矢量部分; 还定义了陀螺仪和四元数的微分关系以及四元数与n、b两系之间旋转矩阵的关系, 如式(2)和式(3).
| $\left( \begin{array}{l} {{q'}_0}\\ {{q'}_1}\\ {{q'}_2}\\ {{q'}_3} \end{array} \right) = \frac{1}{2}\left( {\begin{array}{*{20}{c}} 0&{ - \omega _x^b}&{ - \omega _y^b}&{ - \omega _z^b}\\ {\omega _x^b}&0&{\omega _z^b}&{ - \omega _y^b}\\ {\omega _y^b}&{ - \omega _z^b}&0&{ - \omega _x^b}\\ {\omega _z^b}&{\omega _y^b}&{ - \omega _x^b}&0 \end{array}} \right)\left( \begin{array}{l} {q_0}\\ {q_1}\\ {q_2}\\ {q_3} \end{array} \right){\rm{ = }}\frac{1}{2}{\Omega _{{b}}}.q$ | (2) |
| $C_{{n}}^{ b} = \left( {\begin{array}{*{20}{c}} {q_0^2 + q_1^2 + q_2^2 + q_3^2}&\!\!\!\!\!\!{2({q_1}{q_2} + {q_0}{q_3})}&\!\!\!\!\!\!{2({q_1}{q_3} + {q_0}{q_2})}\!\!\!\!\!\!\!\! \\ {2({q_1}{q_2} + {q_0}{q_3})}&\!\!\!\!\!\!{q_0^2 + q_1^2 + q_2^2 + q{{_3^2}}}&\!\!\!\!\!\!{2({q_2}{q_3} + {q_0}{q_1})} \\ {2({q_1}{q_3} + {q_0}{q_2})}&\!\!\!\!\!\!\!\!{2({q_2}{q_3} + {q_0}{q_1})}&\!\!\!\!\!\!\!\!{q_0^2 + q_1^2 + q_2^2 + q_3^2} \end{array}}\!\!\!\! \right)$ | (3) |
通过一阶龙格库塔法求解四元数微分方程如式(4), T为采样周期. 求出四元数得到旋转矩阵
| $q(t + T) = q(t) + T{\Omega _{\rm b}}(t)q(t)$ | (4) |
| $\left\{\begin{aligned} & \theta = \arcsin (2({q_0}{q_2}- {q_1}{q_3})) \\ & \varphi = \arctan \frac{{2({q_2}{q_3} + {q_0}{q_1})}}{{(1 - 2(q_1^2 + q_2^2))}} \\ & \psi = \arctan \frac{{2({q_1}{q_2} + {q_0}{q_3})}}{{1- 2(q_2^2 + q_3^2)}} \end{aligned}\right. $ | (5) |
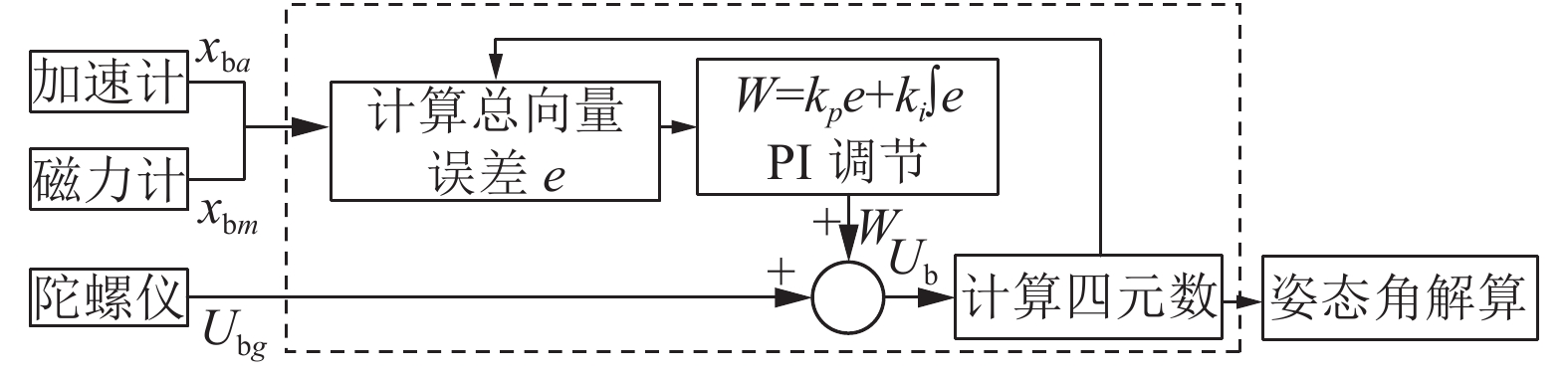
由于陀螺仪存在长时间工作会误差漂移、加速计存在动态响应较慢、磁力计存在数据采集容易受环境影响等因素, 在具体应用时往往还会将这三者数据进行补偿从而获得准确的姿态[18–22]. 图4就是一种典型的互补滤波姿态解算算法[20].
|
图 4 基于MEMS的姿态角互补滤波算法框图 |
图4中, 虚线部分为互补滤波的过程, xba为b系载体的加速度, n系中标准重力加速度gn=[0,0,1]T, 通过旋转矩阵表示为b系标准重力加速度并与xba做向量积, 得到b系下加速度向量误差; xbm为b系载体的磁力, 通过旋转矩阵将xbm转到n系下表示xnm=[hx,hy,hz]T, n系下磁力计理想输出数据[bx,by,bz]T与xnm的关系为
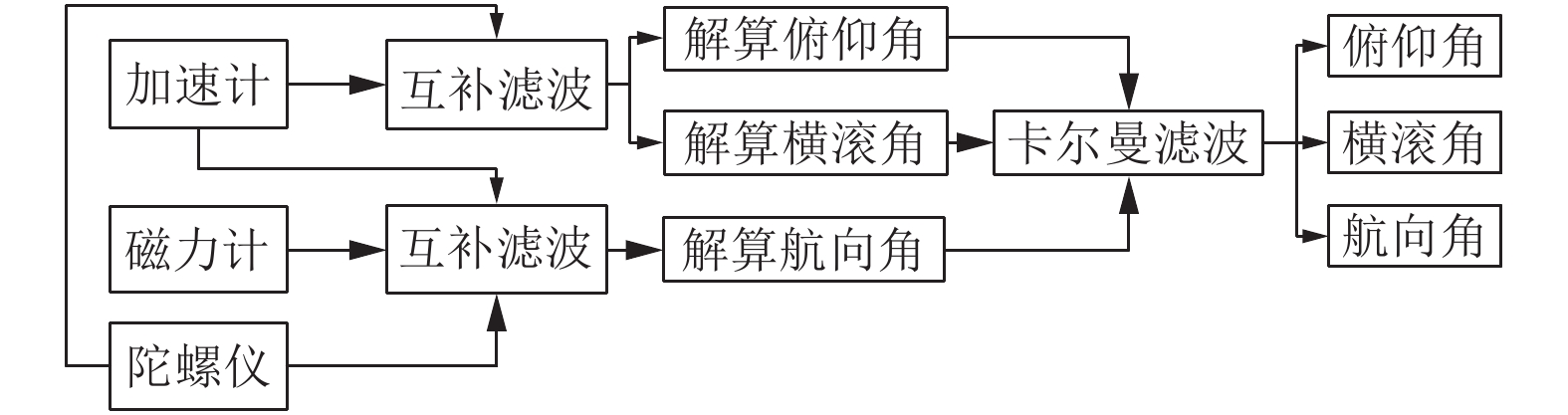
由于MEMS磁力计数据易受周围金属影响以及互补滤波的截止频率不易确定[21,22], 解算后电梯姿态角的误差较大, 精度不高, 所以在互补滤波姿态解算上开展进一步工作, 由此, MEMS四元数卡尔曼滤波算法的电梯姿态求解如图5所示. 首先, 在解算俯仰角和横滚角时, 把互补滤波方法中使用的磁力计参数排除, 仅用加速计数据计算向量误差来校正陀螺仪, 来避免磁力计数据误差对横滚角和俯仰角计算的影响; 其次, 卡尔曼滤波是最优递推估计技术, 其中线性化的扩展卡尔曼滤波(EKF)已经广泛用于工业非线性系统[23], 结合电梯运行规律以及姿态估计系统的非线性特点, 通过扩展卡尔曼滤波将初步解算的姿态角作为观测量对预测量进行修正, 以便得到当前时刻的最优状态估计, 从而帮助提高电梯姿态角的精度.
|
图 5 四元数卡尔曼滤波的姿态解算图 |
EKF是将卡尔曼滤波状态方程和测量方程非线性部分线性化, 得到线性模型如式(6)和式(7):
| $X(k) = AX(k - 1) + W(k)$ | (6) |
| $Z(k) = HX(k) + V(k)$ | (7) |
预测更新过程如下:
1) 状态一步预测
| $X(k|k - 1) = AX(k - 1|k - 1)$ | (8) |
式中, X(k|k–1)是用k–1时刻状态预测的结果, X(k–1|k–1)是k–1时刻状态最优结果.
2) 状态一步预测协方差
| $P(k|k - 1) = AP(k - 1|k - 1)A^{\rm T} + Q$ | (9) |
式中, P(k|k–1)是X(k|k–1)的协方差, P(k–1|k–1)是X(k–1|k–1)的协方差, Q为系统噪声协方差.
3) 卡尔曼增益
| $Kg(k) = P(k|k - 1)H^{\rm T}/(HP(k|k - 1)H^{\rm T} + R)$ | (10) |
式中, R为测量噪声协方差.
4) 状态更新
| $X(k|k) = X(k|k - 1) + Kg(k)(Z(k) - HX(k|k - 1))$ | (11) |
5) 状态协方差更新
| $P(k|k) = (1 - Kg(k)H)P(k|k - 1)$ | (12) |
式中, X(k)为状态值用于状态预测, 式(7)中Z(k)为初步解算后的姿态角, 式(8)~式(10)是状态估计部分, 即当前时刻预测值和协方差以及增益; 式(11)和式(12)是状态更新的部分即当前时刻的最优状态, 然后将当前时刻的电梯最优姿态估计用于下一个时刻的预测, 最终得到精确后的电梯姿态角.
3.3 电梯速度计算根据数学知识可知, 加速度在时间上的积分等于速度, 积分的值可无限近似成区域面积的总和. 由于实际采样时间不趋于0这样会有误差累加的情况出现. 为了减少误差, 通过以下方法来求得电梯速度:
| $ V = S\!ample(n - 1)*T + (S\!ample(n) - S\!ample(n - 1)/2)*T $ |
其中, Sample(n)为当前时刻加速度, Sample(n–1)为前一时刻加速度, T为时间间隔.
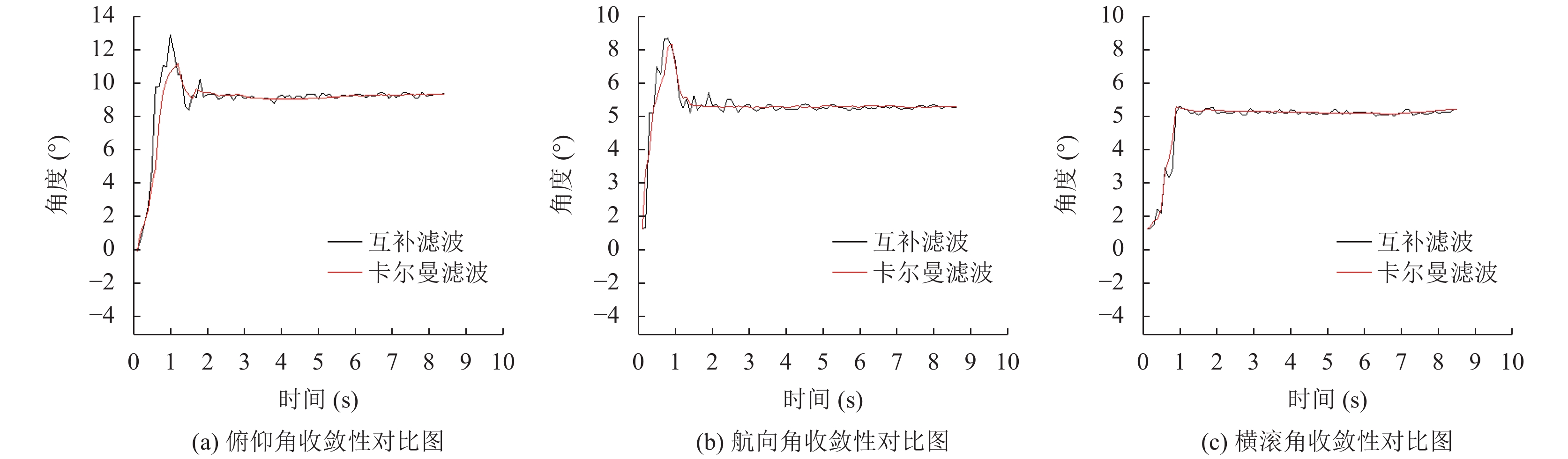
3.4 滤波性能分析就互补滤波算法与卡尔曼滤波算法在收敛性进行对比分析, 如图6所示. 卡尔曼滤波的姿态角比较于互补滤波的姿态角抖动较小, 滤波的收敛效果更好, 具有良好的实时性.
|
图 6 互补滤波和卡尔曼滤波的收敛性分析图 |
4 实验分析 4.1 电梯姿态解算算法优化比对
为验证本方法的效果, 在2015年安装使用的某电梯上安装了本装置, 分别应用常规互补滤波法、本算法进行俯仰角、航向角以及横滚角结算, 对比如图7所示. 本方法解算的姿态角相对平滑, 抖动小.
4.2 电梯运行状态的数据分析为进一步对比验证本方法的合理性, 电梯A及电梯B分别安装了本装置, 对解算的姿态角进行分析. 图8~图10为电梯A和电梯B某时段横滚角、俯仰角、航向角的对比数据. 可以看出, 两部电梯在运行过程中横滚角和俯仰角的偏离值只有零点几度. 但在航向角的比较中, 电梯A的偏离值为14而电梯B的偏离值为8, 两者相差较大, 导致电梯A的晃动感较为明显.

|
图 7 互补滤波姿态解算和本文算法姿态解算角度对比图 |

|
图 8 电梯A和B横滚角对比图 |

|
图 9 电梯A和B俯仰角对比图 |
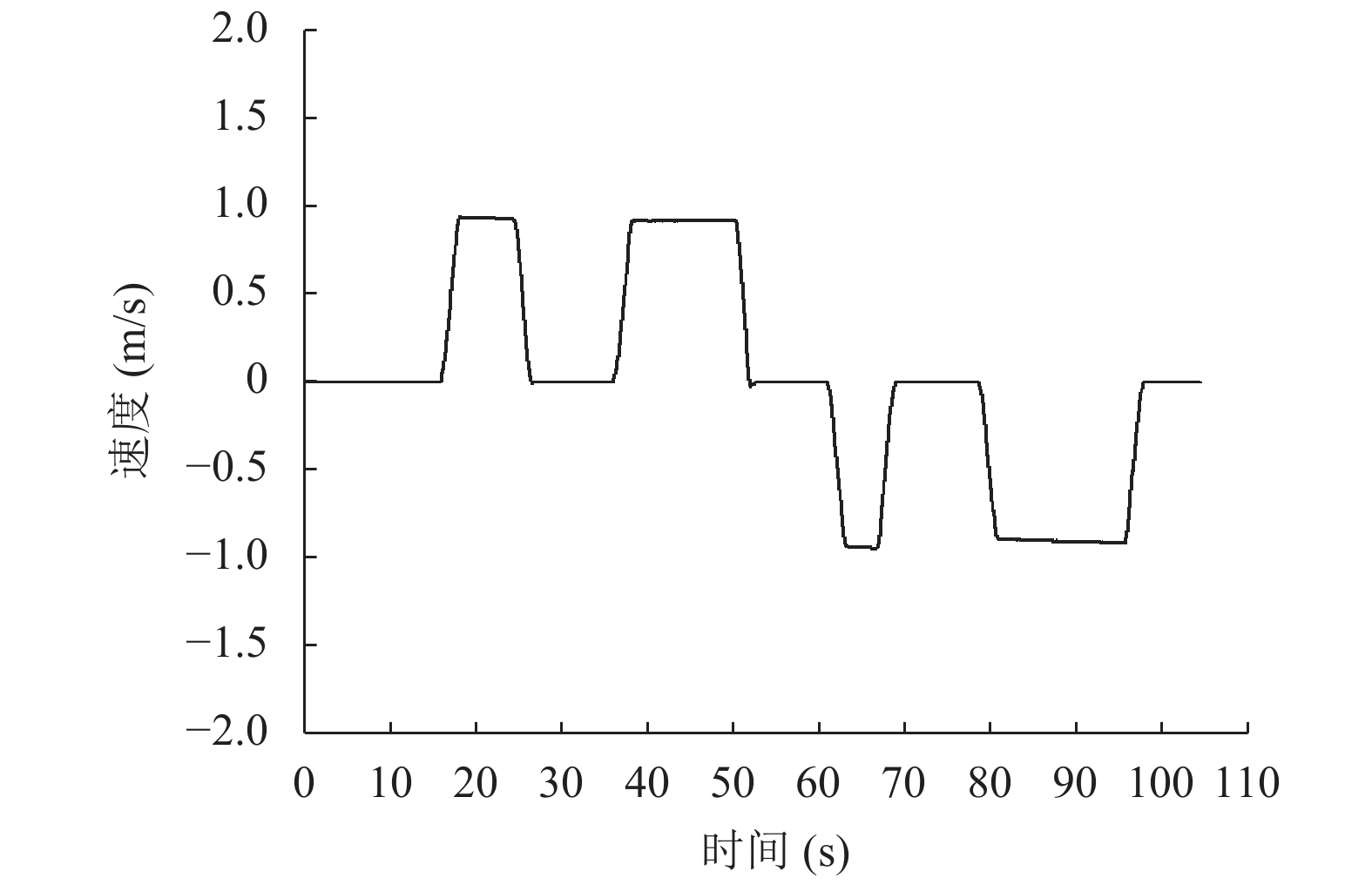
图11为电梯A速度数据, 图12为电梯B速度数据, 速度正值表示电梯为上行姿态, 速度负值表示电梯为下行姿态, 速度为零时则表示电梯静止, 通过速度可知电梯的当前状态; 可见, 电梯B在上下运行过程中的速度略快于电梯A.

|
图 10 电梯A和B航向角对比图 |
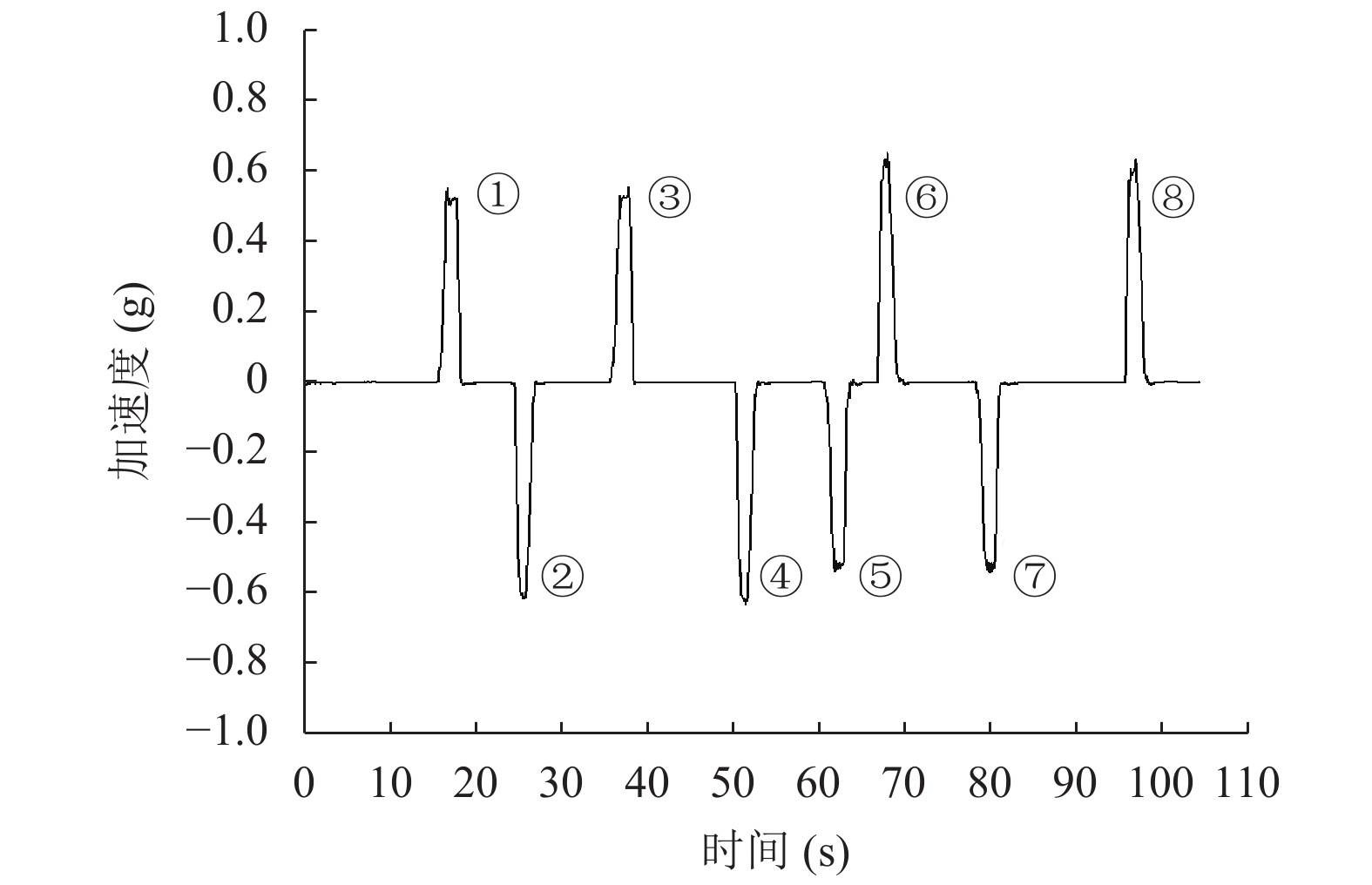
图13为电梯A的加速度, 图14为电梯B的加速度, 可知两者的加速度数据总体正常. 统计学中定义峰度为波形尖峭程度的一个量[24], 采用峰度来表示电梯加速度的波形特征, 可以较好地比较两部电梯的舒适性, 峰度越大即加速度波形越尖锐, 说明电梯在加减速的过程越急速, 导致不舒适的乘坐感, 峰度越小即加速度波形越平滑电梯在加减速的过程越平缓能带来良好的乘坐体验. 由表1和表2得出, 电梯A的峰度比电梯B来的大, 即电梯A的舒适性不如电梯B.
因此, 综合电梯的横滚角、俯仰角、航向角以及加速度峰度可以得出结论为, 电梯A的舒适性与安全性皆不如电梯B, 这和电梯A、电梯B的实际情况相吻合; 电梯A为2007年投入使用的货梯, 长时间大负荷使用导致器械老化, 电梯B为2016年投入使用的客梯, 设施状况和维保较好.
|
图 11 电梯A的速度图 |

|
图 12 电梯B的速度图 |
|
图 13 电梯A的加速度图 |
5 总结
在电梯监测中应用九轴MEMS传感器, 在应用四元数算法时需结合电梯金属件多、运行突变性较小、姿态变化率不大等运行特点, 首先在求解横滚角和俯仰角时用加速计数据而不是磁力计数据来校正陀螺仪, 其次, 用卡尔曼滤波算法来预测估计电梯状态, 最终提高了解算电梯姿态角的精度; 通过分析电梯运行时的姿态角和加速度的峰度以及电梯的速度, 为评估对电梯的安全性与舒适性提供了数据支持.

|
图 14 电梯B的加速度图 |
| 表 1 电梯A加速度波形的峰度 |
| 表 2 电梯B加速度波形的峰度 |
| [1] |
潘鹏, 吴允平, 王廷银, 等. 基于Logistic回归的电梯健康评估. 计算机系统应用, 2018, 27(10): 255-260. DOI:10.15888/j.cnki.csa.006531 |
| [2] |
恩旺, 刘子金, 张淼. 中国电梯行业的技术发展与趋势. 建筑科学, 2018, 34(9): 110-118. |
| [3] |
李东风. 基于物联网技术的电梯安全运行监控系统. 通信设计与应用, 2017(17): 8-9. |
| [4] |
施京京. 不断提升电梯安全水平——《关于加强电梯质量安全工作的意见》解读. 中国质量技术监督, 2018(3): 18-19. DOI:10.3969/j.issn.1008-1607.2018.03.006 |
| [5] |
姚长鸿, 夏钟兴. 电梯轿厢舒适度与异常震动监测系统的设计探讨. 价值工程, 2016, 35(9): 87-88. |
| [6] |
顾雯雯, 孙勇, 路成龙. 影响电梯乘坐舒适度因素分析. 中国设备工程, 2018(24): 59-60. DOI:10.3969/j.issn.1671-0711.2018.24.035 |
| [7] |
宋涵, 郑尚透. 基于AHP综合评价法的电梯舒适度评估体系研究. 机电工程技术, 2019, 48(2): 21-22, 81. DOI:10.3969/j.issn.1009-9492.2019.02.006 |
| [8] |
曹景伟, 朱宝全. 应用MEMS陀螺仪和加速度计的汽车运动姿态测量. 重庆理工大学学报(自然科学), 2018, 32(4): 48-54. |
| [9] |
王贇贇, 李建民, 侯文. 基于组合导航的汽车姿态数据采集系统设计. 电子产品世界, 2017, 24(1): 44-47, 26. |
| [10] |
Shi G, Li XS, Jiang ZF. An improved yaw estimation algorithm for land vehicles using MARG sensors. Sensors, 2018, 18(10): 3251. DOI:10.3390/s18103251 |
| [11] |
刘飞飞, 任安虎, 张博超. MPU9250九轴传感器的危岩危石监测系统. 单片机与嵌入式系统应用, 2018, 18(12): 62-65, 73. |
| [12] |
张煌军, 徐雪松, 罗伟, 等. 基于平方根容积卡尔曼滤波的四旋翼无人机的姿态解算. 科学技术与工程, 2019, 19(12): 248-253. DOI:10.3969/j.issn.1671-1815.2019.12.036 |
| [13] |
王龙, 章政, 王立. 改进扩展卡尔曼滤波的四旋翼姿态估计算法. 计算机应用, 2017, 37(4): 1122-1128. DOI:10.11772/j.issn.1001-9081.2017.04.1122 |
| [14] |
孙章国. 基于ARM的航姿参考系统研究[硕士学位论文]. 上海: 上海交通大学, 2010.
|
| [15] |
周绍磊, 丛源材, 李娟, 等. 方向余弦矩阵中四元数提取算法比较. 中国惯性技术学报, 2008, 16(4): 415-418. |
| [16] |
张荣辉, 贾宏光, 陈涛, 等. 基于四元数法的捷联式惯性导航系统的姿态解算. 光学精密工程, 2008, 16(10): 1963-1970. |
| [17] |
泰永元. 惯性导航. 2版. 北京: 科学出版社, 2014.
|
| [18] |
Mahony R, Hamel T, Pflimin JM. Nonlinear complementary fllters on the special orthogonal group. IEEE Transactions on Automatic Control, 2008, 53(5): 1203-1218. DOI:10.1109/TAC.2008.923738 |
| [19] |
彭孝东, 张铁民, 李继宇, 等. 基于传感器校正与融合的农用小型无人机姿态估计算法. 自动化学报, 2015, 41(4): 854-860. |
| [20] |
李二闯, 张建杰, 袁亮, 等. 基于四元数互补滤波的小型四旋翼姿态解算. 组合机床与自动化加工技术, 2019, 37(3): 37-39, 43. |
| [21] |
杜瑾, 赵华超, 郑哲, 等. 捷联惯导互补滤波姿态融合算法设计. 传感技术学报, 2018, 31(10): 1547-1552. |
| [22] |
孙金秋, 游有鹏, 傅忠云. 基于共轭梯度法和互补滤波相结合的姿态解算算法. 传感技术学报, 2014, 27(4): 524-529. DOI:10.3969/j.issn.1004-1699.2014.04.019 |
| [23] |
叶松庆. 非线性卡尔曼滤波算法研究[硕士学位论文]. 重庆: 中国科学院重庆绿色智能技术研究院, 2016.
|
| [24] |
王学民. 偏度和峰度概念的认识误区. 统计与决策, 2008(12): 145-146. |
 2020, Vol. 29
2020, Vol. 29


