1 引言

文本分类^[1]方法的研究已经超过了50年, 该类方法大多被应用于专题文献分类. 然而, 随着科技的发展和创新, 跨学科领域如计算社会科学^[2]、公共卫生监测^[3]和流行病学^[4]等都对文本分类提出了新要求. 这些领域的待分类对象通常是在线文本^[5], 预测标签则可能是健康状况、政治立场或人类表情等差异化的术语. 这些变化对文本分类(或称为文档分类)提出了新要求和新挑战.

目前, 已有很多研究者对文本分类进行了探讨和研究, 如文献[6]为了提取更多的可信反例和构造准确高效的分类器, 提出一种基于聚类的半监督主动分类方法, 该方法利用聚类技术和正例文档共享尽可能少的特征, 从未标识数据集中尽可能多地移除正例, 但该方法仅适用于较少文本特征的情况. 文献[7]中提出一种基于聚类的改进KNN算法, 采用改进统计量方法进行文本特征提取, 依据聚类方法将文本聚类为几个簇, 最后利用改进的KNN方法对簇类进行分类, 但该方法难以提高文本分类效率. 还有一些学者开发出控制混杂因子^[8]的方法, 包括匹配^[9]、分层和回归分析^[10]. 文献[11]开发出了用于因果图模型的测试方法, 用于确定哪种结构允许使用后门调整对混杂因子进行控制. 文献[12]提出了一种基于LDA模型的文本分类方法, 应用LDA概率增长模型对文本集进行主题建模, 在文本集的隐含主题-文本矩阵上训练SVM, 构造文本分类器, 具有较好的分类效果.

上述方法各有特点, 但其主要缺点是: 混杂变量不能得到很好地控制, 从而造成分类器的错误输出. 本文的目的是对影响分类的因子进行控制和调整, 使得文本分类器具有良好的准确性和鲁棒性. 因此, 本文基于Pearl的后门调整方法^[11], 提出了一种基于协变量调整的文本分类方法, 该方法以训练阶段的混杂变量为条件, 在预测阶段计算出混杂变量的总和. 另外, 本文还进一步探讨了该方法的参数影响, 以允许对预期调整的强度进行调整. 实验结果表明, 所提方法能够提高分类器的鲁棒性, 即使在混杂因子与目标变量之间的关联从训练集到测试集发生倒置的极端情况下, 也能保持较高的准确度.

2 用于文本分类器的协变量调整 2.1 文本分类中得分协变量调整

假设研究目的是估计变量X对变量Y的因果效应, 但无法进行随机对照实验. 则已知混杂因子变量Z的一个充分集, 可以使用式(1)估计对因果关系:

$p(y|do(x)) = \sum\limits_{{\textit{z}} \in Z} {p(y|x,{\textit{z}})p({\textit{z}})} $

(1)

该公式称作协变量调整(也称为后门调整). 协变量标准是一个图形化测试, 决定Z是否是估计因果效应变量的一个充分集, 并要求Z中不存在X的子节点, 且Z会阻止X和Y之间包含指向X的每一条路径. $p(y|x) \ne p(y|do(x))$ , 其中的符号“do”表示假设X=x.

协变量调整已经在因果推理问题中得到了充分研究, 但本文的研究是文本分类中的应用. 假设已知一个训练集 $D = \{ ({x_i},{y_i},{{\textit{z}}_i})\} _{i = 1}^n$ , 集合中的每个实例均包含一个术语特征向量x, 一个标签y和一个协变量z. 本文的目的是对一些新实例 ${x_i}$ 的标签 ${y_i}$ 进行预测, 同时控制一个未观测到的混杂因子 ${{\textit{z}}_i}$ . 也即: 本文假设混杂因子可在训练阶段观察到, 但无法在测试阶段观察到.

所提方法的有向图模型如图1所示, 给出了对文本分类的一种省略混杂因子Z的判别式方法, 假设混杂因子对 $P\left( {Y|Z} \right) $ 中的向量和目标标签均有影响, 用已观察到的向量x为条件的logistic回归分类器对 $P(Y|X)$ 进行建模, 该模型的结构确保Z可以满足用于调整的协变量标准.

虽然协变量调整方法通常用于识别X对Y的因果关系, 但并没有解释任何因果关系. 然而, 式(1)给出了一个框架, 在控制Z中X为已知时, 作出对Y的预测. 这样, 可以训练一个分类器, 对 $P(Y|Z)$ 从训练数据到测试数据发生变化的情况下具备鲁棒性.

本文使用式(1)对测试样本x进行分类. 假设对于训练样本, z为已观测状态, 但没有在测试样本中观察到. 因此, 需要从已标记的训练数据中估计两个变量 $p(y|x,{\textit{z}})$ 和 $p({\textit{z}})$ . 假设 ${x_i}$ 是一个二进制特征向量, ${y_i}$ 和 ${{\textit{z}}_i}$ 则是二进制变量. 对于 $p({\textit{z}})$ , 可使用最大似然估计:

$p({\textit{z}} = k) = \frac{{\displaystyle \sum\limits_{i \in D} {1[{{\textit{z}}_i} = k]} }}{{|D|}}$

(2)

式中, $1[ \cdot ]$ 是一个指示函数; D表示训练集; $p({\textit{z}})$ 表示为训练集中指示函数之和与训练集样本数的比例. 对于 $p(y|x,{\textit{z}})$ , 使用L2-正则化logistic回归, 计算过程可以参考文献[13].

2.2 对调整强度进行调节

从实施的角度来看, 上述方法可表述为: 使用上述最大似然估计(Maximum Likelihood Estimation, MLE)计算出 $p({\textit{z}})$ . 本文通过对每个实例 ${x_i}$ , 附加上两个分别表示z=0和z=1的额外特征 ${c_{i,0}}$ 和 ${c_{i,1}}$ , 高效地计算出 $p(y|x,{\textit{z}})$ . 如果 ${{\textit{z}}_i} = 0$ , 将第一个特征设为 ${v_1}$ , 将第二个特征设为0; 若 ${{\textit{z}}_i} = 1$ , 则将第二个特征设为 ${v_1}$ , 将第一个特征设为0. 默认情况下设 ${v_1} = 1$ , 但可因情况而定. 为了对一个新实例进行预测, 使用式(1)计算后验概率.

考虑到术语特征向量x通常包含数以千计的元素变量, 而协变量z添加两个额外特征就能够对分类产生较大影响. 为了理解这一点, 可以考虑正则化logistic回归中的权重训练不足的问题^[13]. 由于在文本分类中使用了数以千计的相互联系和重叠的变量, 对一个logistic回归模型进行的优化涉及到相关变量系数间的权衡问题, 以及由L2正则化惩罚所决定的系数量级. 在这个设定中, 少数高预测性特征的存在会导致低预测性特征的系数低于期望数值, 因为高预测性特征在模型中占据主导地位, 会导致在低预测性特征设定中的模型性能较差. 因此, 本文通过引入z的特征(一个潜在的高预测性特征), 故意对x中的术语系数进行不充足训练. 例如, 若z指的是性别, 则通过使用协变量调整, 使得与其他术语相比, 性别指示性术语具有相对较低量级的系数. 通过对协变量调整的强度进行调节, 改写了L2正则化logistic回归^[13]对数似然函数, 对术语向量的系数和混杂因子的系数进行区分:

$\begin{aligned}[b] L(D,\theta ) = & \sum\limits_{i \in D} {\log {p_\theta }({y_i}|{x_i},{{\textit{z}}_i})} \\ & - {\lambda _x}\sum\limits_k {{{(\theta _k^x)}^2}} - {\lambda _{\textit{z}}}\sum\limits_k {{{(\theta _k^{\textit{z}})}^2}} \end{aligned} $

(3)

式中, ${\theta ^x}$ 为术语向量系数; ${\theta ^{\textit{z}}}$ 为混杂因子系数; $\theta $ 为 ${\theta ^x}$ 和 ${\theta ^{\textit{z}}}$ 的串联参数; ${\lambda _x}$ 和 ${\lambda _{\textit{z}}}$ 分别为控制术语系数和混杂因子系数的正则化强度. 在默认情况下设 ${\lambda _{\textit{z}}} = {\lambda _x} = 1$ . 但是, 通过设 ${\lambda _{\textit{z}}} < {\lambda _x}$ , 能够降低混杂因子系数 ${\theta ^{\textit{z}}}$ 的量级惩罚. 这使得系数 ${\theta ^{\textit{z}}}$ 在分类决策中发挥比 ${\theta ^x}$ 更重要的作用, 并增加 ${\theta ^x}$ 中不充分训练的数量. 本文通过提高 ${v_1}$ 的混杂因子特征数值, 同时将其他特征数值保持为0, 达到这个效果. 由于本文没有将特征矩阵标准化, 增加 ${v_1}$ 的数值同时保持x的数值不变, 能够促使 ${\theta ^{\textit{z}}}$ 的数值较小, 并有效地使得对 ${\theta ^{\textit{z}}}$ 的L2惩罚相对小于 ${\theta ^x}$ .

3 实验与分析

本文使用了3个公开数据集进行实验, 其中混杂因子Z和分类变量Y之间的关系在训练集和测试集中有所差异. 有以下两种情况: 直接控制训练和测试数据之间的差异; Z和Y之间的关系发生了突然.

为对具有不同的 $P(Y|Z)$ 分布的训练/测试集进行采样, 假设已有包含元素 $\{ ({x_i},{y_i},{{\textit{z}}_i})\} $ 标注后的数据集 ${D_{\rm{train}}}$ 和 ${D_{\rm{test}}}$ , 其中 ${y_i}$ 和 ${{\textit{z}}_i}$ 为二进制变量. 本文引入了一个偏差参数 $P(y = 1|{\textit{z}} = 1) = b$ ; 根据定义可知 $P(y = 0| {\textit{z}} = 1) =$ $ 1 - b$ . 对于每个实验, 从每个集合进行不放回抽样 ${D'_{\rm{train}}} \subseteq $ $ {D_{\rm{train}}}$ , ${D'_{\rm{test}}} \subseteq {D_{\rm{test}}}$ . 为了模拟 $P(Y|Z)$ 中的变化, 对于训练和测试使用不同的偏差项 ${b_{{\rm{train}}}}$ 和 ${b_{{\rm{test}}}}$ . 因此, 根据以下约束条件进行采样:

1) $ {P_{{\rm{train}}}}(y = 1|{\textit{z}} = 1) = {b_{{\rm{test}}}} $ ;

2) $ {P_{{\rm{test}}}}(y = 1|{\textit{z}} = 1) = {b_{{\rm{test}}}} $ ;

3) $ {P_{{\rm{train}}}}(Y) = {P_{{\rm{test}}}}(Y) $ ;

4) ${P_{{\rm{train}}}}(Z) = {P_{{\rm{test}}}}(Z)$ .

其中, 3)和4)的两个约束条件是为了隔离对 $P(Y|Z)$ 中的变化影响. 因此, 从训练数据到测试数据中, 保持 $P(Y)$ 和 $P(Z)$ 不变, $P(Y|Z)$ 则会发生变化. 本文对 $P(Y,Z|X)$ 的联合分布进行建模, 使用一个logistic回归分类器, 其中标签在Y和Z的积空间中. 在测试阶段, 本文对z的可能分配进行求和, 以计算y的后验分布.

3.1 实验数据及设置

为构建微博数据集, 本文使用微博信息流应用编程接口采集包含上海和杭州地理坐标的博文. 该实验在4天时间中(2016年, 6月15日至6月18日)共收集了246 930条包含上海坐标的博文和218 945条包含杭州坐标的博文. 通过移除删减, 并对采集到的博文进行了二次采样, 保留6000个用户的博文, 使得所有用户的性别和地理位置均匀分布. 其中, 用户的性别作为预测其位置的混杂变量. 因此, 设 ${y_i} = 1$ 表示上海, ${{\textit{z}}_i} = 1$ 表示男性. 构建这个数据集的方式使得数据在4种可能的y/z配对中均匀地分布.

本文对电影评论中的情感进行预测, 并使用来自“豆瓣”等的IMDB电影数据将影片类型作为混杂因子. 该数据集中包括50 000条来自IMDB的影片评论, 这些评论带有正面或负面的情感标签. 移除了英语或中文停用词和出现次数不到10次的术语, 使用一个二进制向量来表示特征的存在与否. 电影是否是由IMDB分类所确定为“动作”类型影片作为一个混杂因子. 由此, 对于动作影片, 本文设 ${{\textit{z}}_i} = 1$ , 对于其他类型影片则设 ${{\textit{z}}_i} = 0$ . 这个数据集在4种可能的标签/混杂因子配对中是不均匀分布的. 大约18%的影片为动作电影, 而对动作电影带有正面情感的评论约占5%.

对于微博和IMDB, 本文在训练/测试中进行了变化模拟, 将训练集和测试集的偏差值b设为0.1–0.9, 并对一些分类模型的准确度进行了比较. 对于每对 ${b_{{\rm{train}}}}$ 和 ${b_{{\rm{test}}}}$ , 抽样5段训练/测试的分割样本, 并计算平均准确度.

3.2 对比的模型

本文对以下模型进行了比较:

协变量调整(BA): 即本文所提方法, 通过设置混杂特征的数值 ${v_1} = 10$ , 进行强度更高的协变量调整的模型, 该模型表示为BAZ10.

Logistic回归(LR): 本文研究的主线是一个标准L2正则化logistic回归分类器, 该分类器不会为混杂因子做任何调整, 仅简单地对 $P(Y|X)$ 进行建模.

二次采样(LRS): 在训练阶段, 一种移除偏差的简单方式是选择数据的子样本, 使得 $P(Y|Z)$ 均匀分布. 当存在一个较强的混杂偏差时, 该方法会丢弃很多实例, 且实例数量会随着混杂因子数量的增加而进一步减少.

匹配(M): 匹配通常被用于从观测研究中评估因果效应. 对于每个y=i, z=j的训练实例, 采样另一个训练实例, 其中y≠i, z=j.

3.3 结果分析

对于微博和IMDB电影数据, 本文分别建立了两组实验. 随着训练和测试偏差的差异变化, 研究测试准确度的变化情况. 另外, 计算Z和Y之间的皮尔森相关性^[14], 并给出在测试阶段和训练阶段相关性的差异.

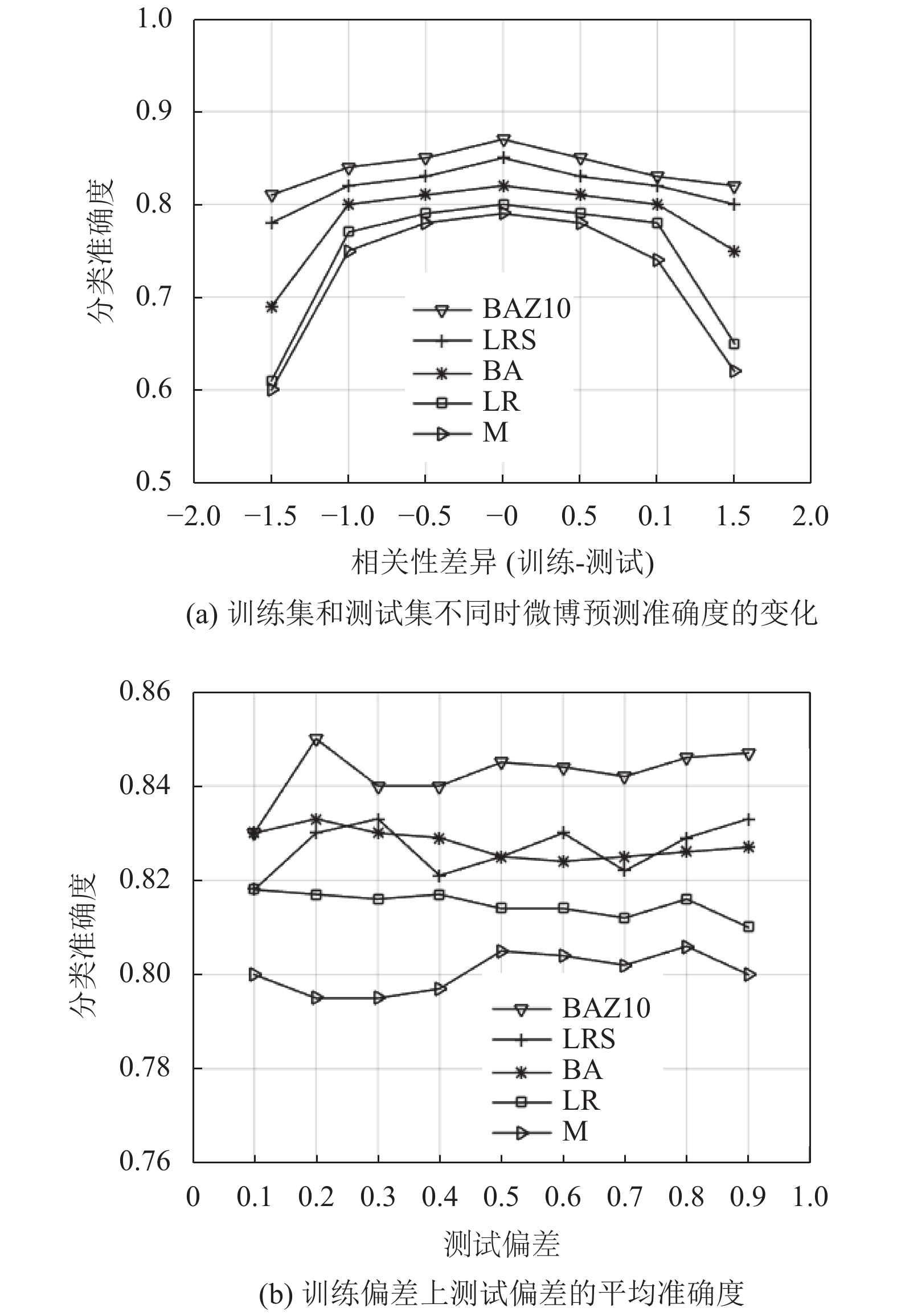
3.3.1 微博实验

微博数据的实验结果如图2所示, 在极值区域表现最佳的方法是BAZ10和LRS. 这两种方法在区间[–1.6, –0.6]和区间[0.6, 1.6]中的性能超过了其他分类器: 与BA方法相比, 超过了15分; 与LR和M方法相比超过了20分; 比SO方法超过了30分. 而在这个区间之外的中间区域, BAZ10方法的性能仅次于BA和LR方法. 此外, 当相关性差异为0时, BAZ10方法的最大准确度损失大约为2分. 这一结果表明, BAZ10方法对混杂因子的鲁棒性明显高于LR方法, 前者在混杂因子影响较小的情况下, 仅会产生最低限度的准确度损失.

在所有训练偏差上, 每个测试偏差的平均准确度如图2(b)所示. BA和BAZ10方法在总体上比其他方法的准确度更高. SO的总体性能不佳, 与其他方法相比, 其准确度要低4到8分.

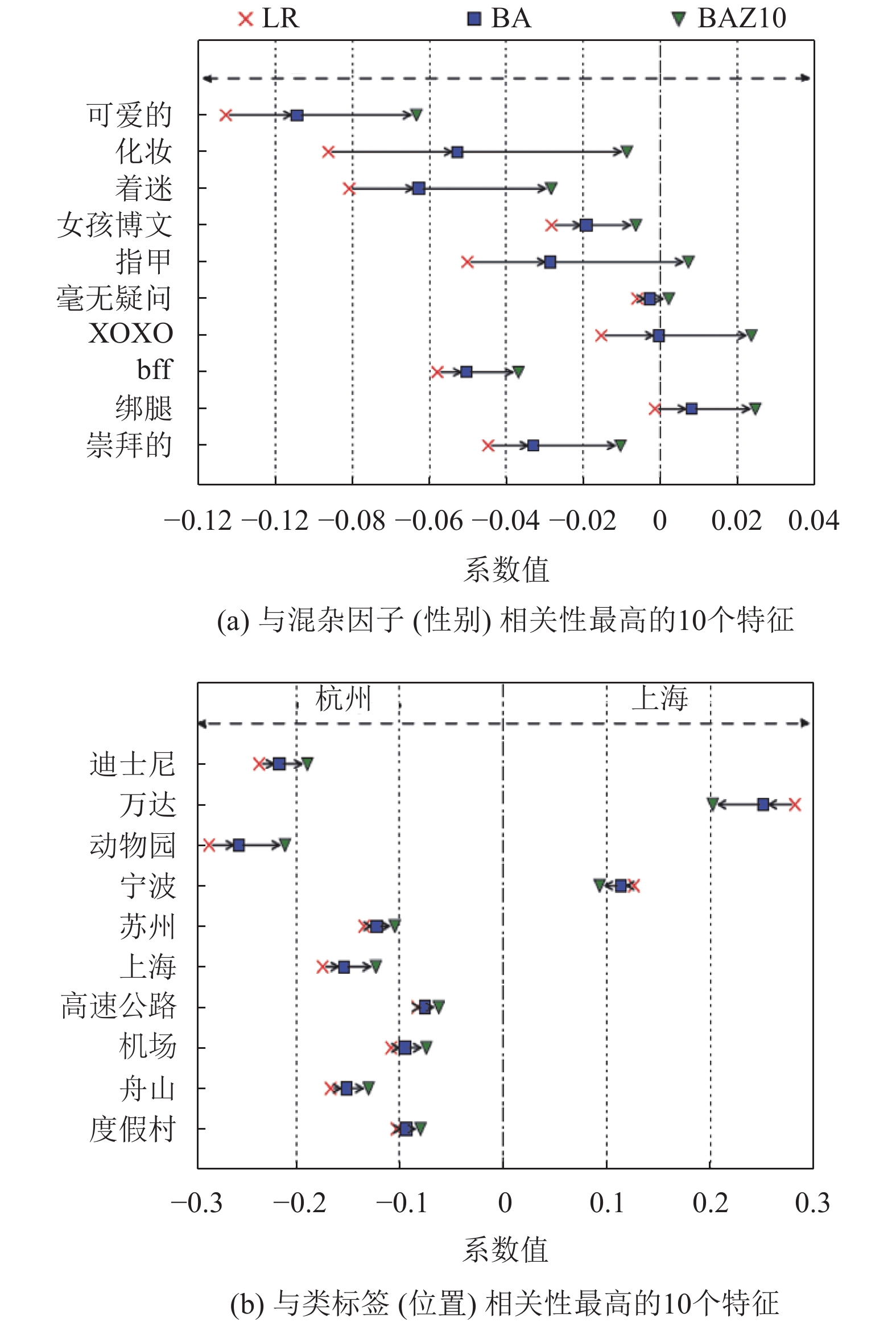
为了找到BAZ10方法比其他方法的准确度和鲁棒性更高的原因, 本文给出了当偏差值为0.9时, LR、BA和BAZ10分类器的系数, 如图3所示. 由图3可知, 根据 ${\chi ^2}$ 统计数据, 10个最能预测类标签的特征和10个最能预测混杂变量的特征. 与位置相关的特征权重在协变量调整方法中有少许下降, 但依然保持相对较重要的地位. 与之相反, 与性别相关的特征权值在协变量调整方法中则非常接近0.

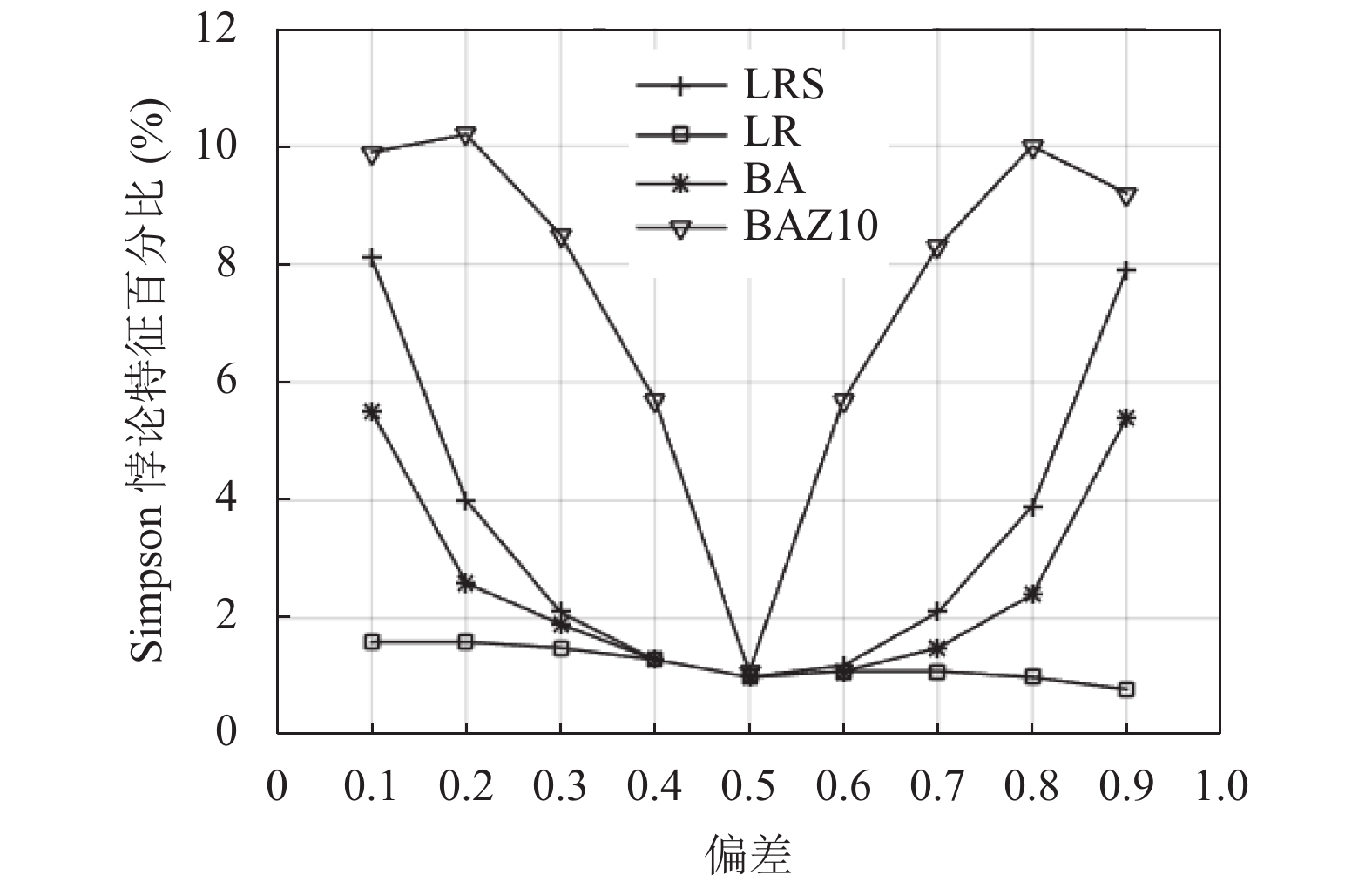
已知拟合数据偏差的强度时, Simpson悖论^[15]的特征百分比如图4所示, 其中, 微博数据中大概包含22 K的特征. 由图可知, BAZ10的Simpson悖论特征数量相对保持不变; 而在其他方法中, 该特征数量则在偏差接近极值时迅速增长.

3.3.2 IMDB实验

图5给出了IMDB数据的实验结果. 结果显示, BA和BAZ10是对混杂偏差的鲁棒性最好的方法. LRS方法鲁棒性最低. LRS方法的结果不理想原因可能是在IMDB数据中, y/z变量的分布不均衡, 使得LRS方法每次仅能在很小比例的训练数据上拟合. 这也是在IMDB实验中, 整体准确度的变化幅度要比微博实验小得多的原因.

3.4 参数分析

对于IMDB和微博实验, 本文还计算了一个成对的t-测试, 以使用相关性差异的每个数值对BAZ10和LR方法进行比较. 实验结果发现, 在19个案例中, BAZ10的性能优于LR; 在8个案例中, LR的性能优于BAZ10; 而在5个案例中, 结果并没有明显差别. 从图中还可以观察到, 当测试数据与训练数据相对于混杂因子非常类似时, BAZ10的性能大致相当或稍弱于LR方法; 然而, 当测试数据在混杂因子上与训练数据不同时, BAZ10的性能要优于LR.

总之, 当在混杂因子的影响中存在极端和突然转变时, 最好的方法是丢弃发生该转变之前的大部分数据. 然而, 一旦在该转变后可用的实例数量适中时, BAZ10方法能够作出调整解决混杂偏差的问题.

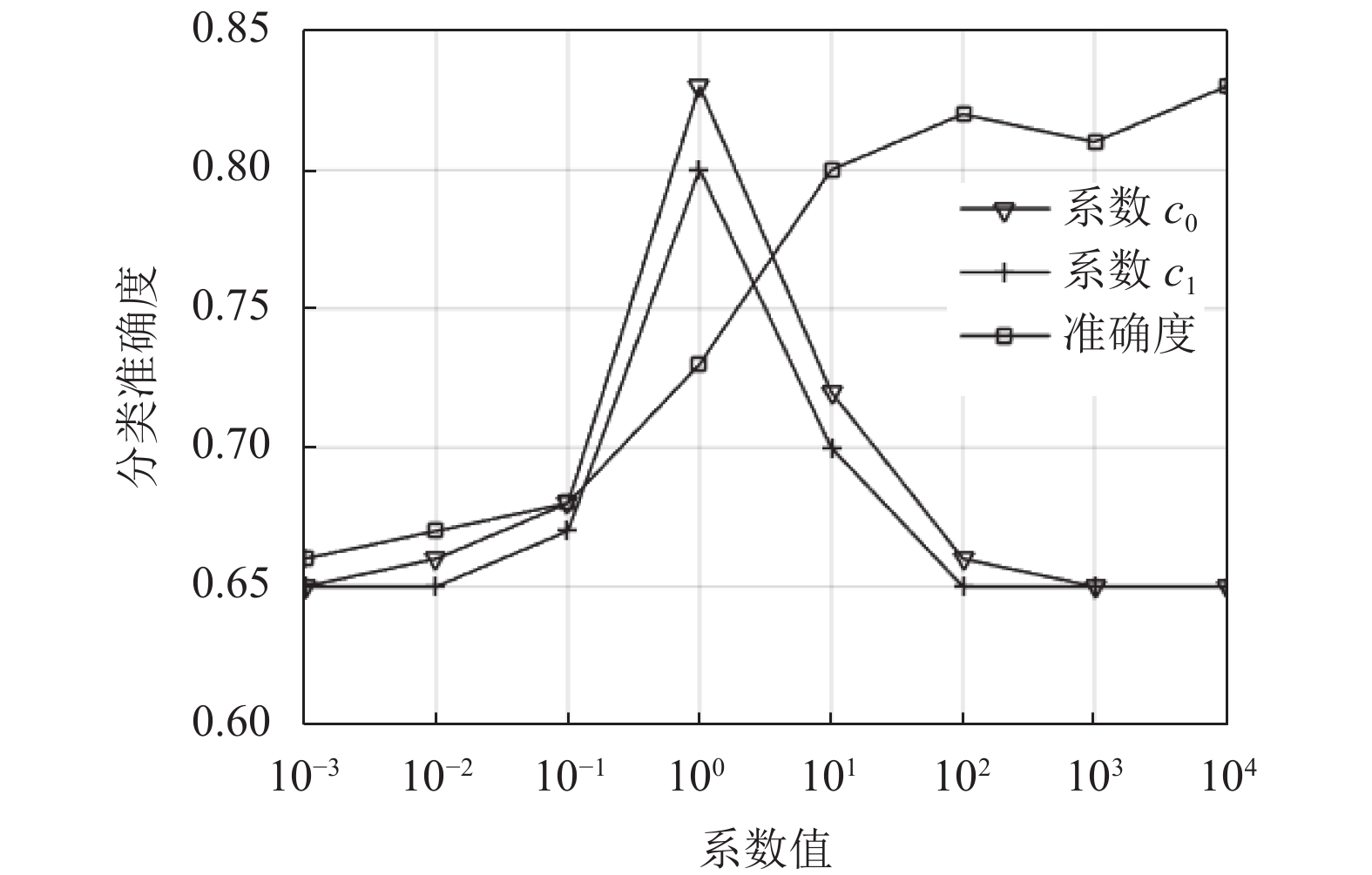
关于参数分析, 本文以BA方法为例, 图6给出了控制着协变量调整强度的 ${v_1}$ 参数影响. 该图给出了 ${c_0}$ 和 ${c_1}$ 成比例系数绝对值的变化, 及当 ${v_1}$ 在微博中增加时准确度的变化. 这些结果是在训练数据集偏差差异较大的情况下产生的, 从图6中可看到, 当 ${v_1}$ 小于10^–1时, 准确度较低, 但较稳定. 然后随 ${v_1}$ 的增加而增长, 并且在 ${v_1} = 10$ 时, 开始大幅攀升. 这个数据集中, 准确度在两个峰值之间出现了15点增益. 对于所有实验中给定 ${v_1} = 10$ , 使用交叉验证可以选择出能够产生期望鲁棒性的 ${v_1}$ 数值.

4 结论与展望

本文提出了一个快速有效的文本分类方法, 即使用协变量调整来控制混杂因子. 在3个不同的数据集上, 本文发现协变量调整能够在混杂关系从训练数据到测试数据发生变化时, 提高分类器的鲁棒性, 并且在混杂偏差很大的情况下, 可以使用一个额外的参数对调整的强度进行调节. 协变量调整不但能够降低与混杂因子相关的系数量级, 而且可以纠正与目标类标签相关联的系数标注.

未来本文将研究在训练阶段仅有Z的带噪估计, 以及Z是一个变量向量的情况.