钓鱼作为一项考验技术、耐力、经验的户外运动, 已经被越来越多人所接受, 而钓鱼活动中最重要的工具就是钓鱼竿, 传统钓鱼竿往往需要通过长时间的钓鱼活动训练和长时间盯着鱼漂才能看漂识鱼, 极大地降低了钓鱼的乐趣. 目前市场上加装传感器的鱼竿一定程度上弥补了传统钓鱼竿的不足, 但此类钓鱼竿依然存在很多缺点: (1)检测装置单一, 缺乏水域监测能力. (2)抗干扰能力较差, 有鱼咬钩时, 报警信号误报率较高, 咬钩时不能准确报警. (3)不具备自动遛鱼功能, 断线跑鱼概率较大.
针对上述情况, 本文利用多种传感器和MCU控制器及外围硬件电路, 通过嵌入式技术和自动化控制技术, 研究一种具有智能选钓位、智能报警及自动遛鱼等功能的新型智能钓鱼竿系统. 该智能钓鱼竿系统将有助于提高钓鱼的精确度, 同时提供一种自动化钓鱼方案, 为在恶劣环境下完成自主钓鱼活动提供可能. 本系统基于卡尔曼滤波的数据融合算法对四元数法解算得到的鱼竿姿态角数据进一步修正, 最优鱼竿姿态角是智能报警和智能遛鱼功能实现的关键. 因此本文主要研究鱼竿姿态解算过程、姿态数据滤波算法及鱼竿自动遛鱼控制算法等内容. 鱼竿姿态解算、控制系统数学模型以及串级PID控制算法的仿真测试结果表明, 控制系统响应良好. 在uC/OS-II操作系统下, 环境传感器及姿态传感器的数据解算实时性良好, 例如鱼竿报警功能, 具有较高灵敏度和准确率, 符合预期目标.
1 智能钓鱼竿系统总体方案设计智能钓鱼竿主要由8个部分组成, 如图1所示, 其中① 为鱼竿杆体, ② 为负责收放线的纺线轮, ③ 为环境检测部分, 该部分主要由温度传感器、光线传感器、溶解氧传感器及深度传感器所组成, 该部分将负责测量待钓水域的环境信息以作为钓位选择的依据, ④ 为姿态传感器部分该部分主要由陀螺仪传感器、加速度计传感器及磁力计传感器所组成, 该部分主要功能为获取鱼竿姿态, ⑤ 为鱼竿手柄该部分, ⑥ 为鱼竿控制部分, 该部分由STM32控制器、电机驱动、电机及报警模块组成, 为智能钓鱼竿控制部分的核心, 其通过鱼竿姿态的变化来实现智能钓鱼竿的报警及遛鱼功能, ⑦ 为电源模块. 该模块主要负责为整个系统供电. ⑧ 为鱼线.
钓鱼竿智能选钓位功能的实现是通过将温湿度传感器、光线传感器、深度传感器、溶氧量传感器及微控制器集成于一个防水球体内, 在钓鱼时, 将此可拆卸的球体随钓鱼钩一起投入待钓水域, 通过球体内的微控制器及传感器采集待钓水域的温度、光线、深度及含氧量等数据, 并通过数据分析预判该水域是否适宜鱼逗留, 进而实现智能选钓位的功能.

|
图 1 智能钓鱼竿示意图 |
钓鱼竿智能报警功能的实现是通过在钓竿顶部安装姿态传感器, 通过姿态传感器中的三轴加速度计采集加速度数据, 三轴磁力计采集磁场数据, 三轴陀螺仪采集角速度数据, 微控制器分别对三轴陀螺仪和三轴加速度计采集到的角速度数据和加速度数据通过卡尔曼滤波算法进行数据融合, 转化为欧拉角进而获取钓竿姿态. 当鱼有咬钩信号时, 鱼竿会有向下的瞬时加速度, 同时鱼竿发生形变即会有一定的倾角变化, 此部分功能将通过瞬时加速度及鱼竿姿态变化倾角作为报警信号, 通过高精度姿态传感器获取鱼竿姿态变化, 能更加有效的捕捉到鱼咬钩的轻微信号, 这将极大地减少误判率进而改进目前市场大多鱼竿报警率低的问题.
钓鱼竿智能遛鱼功能通过自动化控制技术实现, 通过测量及预判鱼线实时拉力值, 建立鱼竿物理模型, 利用鱼竿姿态倾角变化来驱动电机, 可有效控制鱼线收放过程, 使遛鱼过程中鱼线始终处于鱼线的最佳拉力值附近, 从而减少断线跑鱼的概率, 实现智能遛鱼功能.
2 智能钓鱼竿系统硬件部分设计智能钓鱼竿系统硬件部分设计框图如图2所示. 本文选用STM32F103ZET6微控制器作为智能钓鱼竿核心控制器, 温湿度传感器DHT11和光敏电阻模块作为环境传感器, MPU6050六轴加速度/角速度传感器作为鱼竿姿态采集模块, TB6612FNG作为直流减速电机驱动模块, 12 V聚合物锂电池作为电源模块.

|
图 2 智能钓鱼竿系统硬件部分设计框图 |
3 智能钓鱼竿系统软件部分设计
本部分主要完成以下内容: (1) 四元数法解算鱼竿姿态; (2) 通过建立卡尔曼滤波算法的状态方程和观测方程实现基于卡尔曼滤波的数据融合算法; (3) 建立串级PID算法模型, 并通过Simulink仿真整定PID参数, 进而实现智能钓鱼竿的控制.
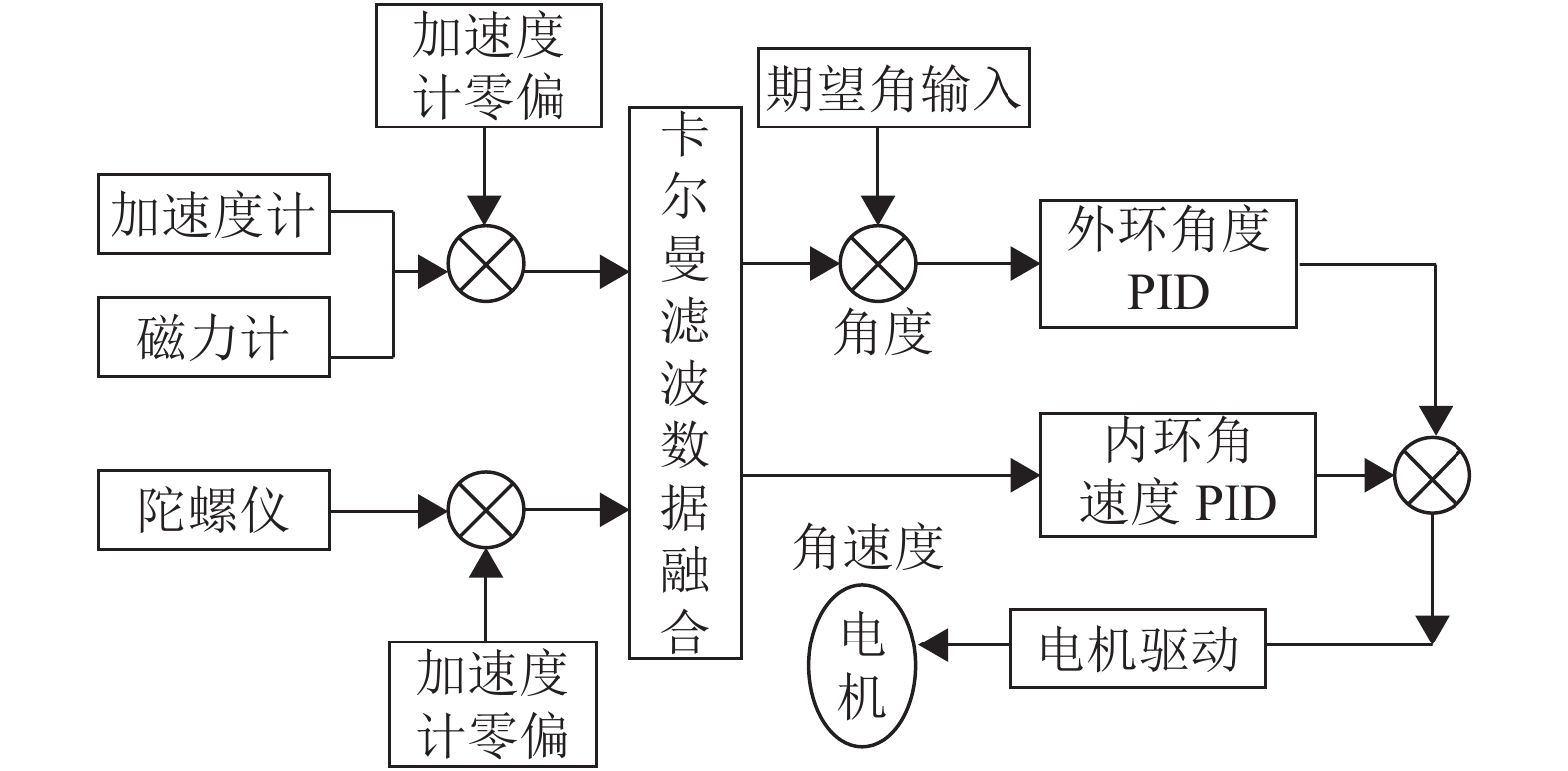
为了实现智能遛鱼功能, 鱼竿电机控制流程如图3, 通过加速度和磁力计得到的姿态角作为卡尔曼数据融合算法的测量值, 将陀螺仪传感器得出的姿态角作为预测值, 通过卡尔曼滤波数据融合得到精准姿态角. 将由数据融合的到的姿态角作为串级PID算法的输入量, 通过外环角度PID和内环角速度PID算法求出电机控制调节量, 通过电机驱动来控制电机转向和转速.
|
图 3 鱼竿电机控制流程图 |
3.1 四元数姿态解算
四元数法是比较常用的姿态解算方法, 通过引入一个四维空间超复数, 当实部为零时, 建立了四维空间和三维空间的联系, 由于角速度积分有累计误差的特性, 因此需要借助加速度分量对四元数矩阵进行修正, 再利用四元数和欧拉角的转换公式即可计算出欧拉角.
图4为智能钓鱼竿四元数姿态解算的流程图. 首先初始状态下, 由四元数和欧拉角的关系确定初始四元数, 姿态传感器采集原始数据并通过均值滤波方法过滤掉高频信号, 然后将四元数的等效余弦矩阵中的重力的分向量归一化后进行向量的叉积运算, 进而求解出陀螺仪的积分误差, 得到准确的角速度后采用一阶龙格库塔法更新四元数和姿态矩阵, 将四元数归一化后即可转换出欧拉角.

|
图 4 四元数姿态解算流程图 |
3.1.1 四元数定义
四元数是一个复数由实部和虚部组成, 四元数的虚部包含3个虚数单位i、j、k, 即四元数可以表示为:
| $Q = {q_0} + {q_1} \cdot i + {q_2} \cdot j + {q_3} \cdot k$ | (1) |
其中, 复数间有以下关系:
| ${i^2} = {j^2} = {k^2} = i \cdot j \cdot k = - 1$ | (2) |
| $\left\{ {\begin{aligned} & i \cdot j = k \\ & j \cdot k = i \\ & k \cdot i = j \end{aligned}} \right.$ | (3) |
| $\left\{ {\begin{aligned} & j \cdot i = - k\\ & k \cdot j = - i\\ & i \cdot k = - j \end{aligned}} \right.$ | (4) |
四元数的矩阵表示形式为:
| $Q = \left( {{q_0},{q_1},{q_2},{q_3}} \right)$ | (5) |
在三维坐标系中, 用四元数表示绕着某个轴的旋转公式可用式(6)来表示, 其中, α表示绕轴旋转的实际角度,
| $\left\{ {\begin{aligned} & {{q_0} = \cos \left( {\frac{\alpha }{2}} \right)} \\ & {{q_1} = \sin \left( {\frac{\alpha }{2}} \right)\cos (\beta x)} \\ & {{q_2} = \sin \left( {\frac{\alpha }{2}} \right)\cos (\beta y)} \\ & {{q_3} = \sin \left( {\frac{\alpha }{2}} \right)\cos (\beta z)} \end{aligned}} \right.$ | (6) |
由于对象是运动的, 所以四元数Q是个变量, 即
| $Q = \frac{1}{2}Q \cdot \omega $ | (7) |
其中, ω为沿坐标系的角速度.
将上述公式展开:
| $\left[ {\begin{array}{*{20}{l}} {{q_0}} \\ {{q_1}} \\ {{q_2}} \\ {{q_3}} \end{array}} \right] = \frac{1}{2} \cdot \left[ {\begin{array}{*{20}{c}} 0&{ - \omega x}&{ - \omega y}&{ - \omega z} \\ {\omega x}&0&{\omega z}&{ - \omega y} \\ {\omega y}&{ - \omega z}&0&{\omega x} \\ {\omega z}&{\omega y}&{ - \omega x}&0 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{q_0}} \\ {{q_1}} \\ {{q_2}} \\ {{q_3}} \end{array}} \right]$ | (8) |
姿态矩阵角速度
四元数转换成方向余弦矩阵: 设有参考坐标系e, 钢体坐标系为b, 假设初始状态e坐标系与b坐标系重合, 则通过四元数可以得出b坐标系旋转至e坐标系的转换矩阵
| $ \begin{array}{l} C_b^e = \\ \!\!\!\!\left[\!\!\!\!\! {\begin{array}{*{20}{c}} {1 - 2 \cdot \left( {q_2^2 + q_3^2} \right)}\!\!\!&\!\!\!{2 \cdot \left( {{q_1} \cdot {q_2} \!-\! {q_0} \cdot {q_3}} \right)}\!\!\!&\!\!\!{2 \cdot \left( {{q_1} \cdot {q_3} \!+\!{q_0} \cdot {q_2}} \right)} \\ {2 \cdot \left( {{q_1} \cdot {q_2} \!+\! {q_0} \cdot {q_3}} \right)}\!\!\!&\!\!\!{1 - 2 \cdot \left( {q_1^2 + q_3^2} \right)}\!\!\!&\!\!\!{2 \cdot \left( {{q_2} \cdot {q_3}\! -\! {q_0} \cdot {q_1}} \right)} \\ {2 \cdot \left( {{q_1} \cdot {q_3}\! -\! {q_0} \cdot {q_2}} \right)}\!\!\!&\!\!\!{2 \cdot \left( {{q_2} \cdot {q_3} \!+\! {q_0} \cdot {q_1}} \right)}\!\!\!&\!\!\!{1 - 2 \cdot \left( {q_1^2 + q_2^2} \right)} \end{array}} \!\!\!\!\right] \end{array}$ | (9) |
通过式(10)可求出由b坐标系转换至e坐标系的坐标
| $\left[ {\begin{array}{*{20}{l}} {{X_e}} \\ {{Y_e}} \\ {{Z_e}} \end{array}} \right] = C_b^e \cdot \left[ {\begin{array}{*{20}{l}} {{X_b}} \\ {{Y_b}} \\ {{Z_b}} \end{array}} \right]$ | (10) |
从方向余弦矩阵欧拉角的转换: 设鱼竿的偏航角为
| $C_e^1 = C_g^1 = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right]$ | (11) |
| $ \begin{aligned} C_1^b & = C_2^b \cdot C_1^2\\ &=\! \left[ {\begin{array}{*{20}{c}} {\cos \phi }&0&{ - \sin \phi } \\ 0&1&0 \\ {\sin \phi }&0&{\cos \phi } \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1&0&1 \\ 0&{\cos \theta }&{\sin \theta } \\ 0&{ - \sin \theta }&{\cos \theta } \end{array}} \right] \\ &=\left[ {\begin{array}{*{20}{c}} {\cos \phi }&{\sin \theta \cdot \sin \phi }&{ - \cos \theta \cdot \sin \phi } \\ 0&{\cos \theta }&{\sin \theta } \\ {\sin \phi }&{ - \sin \theta \cos \phi }&{\cos \theta \cos \phi } \end{array}} \right] \end{aligned}$ | (12) |
| $ c_e^b = c_1^b \cdot c_e^1 = \left[ {\begin{array}{*{20}{c}} {\cos \psi \cos \phi + \sin \theta \sin \phi \sin \psi }&{ - \cos \phi \sin \psi + \sin \phi \cos \psi \sin \theta }&{ - \cos \theta \sin \phi } \\ {\sin \psi \cos \theta }&{\cos \psi \cos \theta }&{\sin \theta } \\ {\sin \phi \cos \psi - \cos \phi \sin \psi \sin \theta }&{ - \sin \phi \sin \psi - \cos \phi \cos \psi \sin \theta }&{\cos \phi \cos \theta } \end{array}} \right]$ | (13) |
我们认为:
由于在坐标系在旋转过程中坐标系一直保持正交关系, 所以有
| $C_b^e = \left( {C_e^b} \right)T = \left[ {\begin{array}{*{20}{c}} {{T_{11}}}&{{T_{21}}}&{{T_{31}}} \\ {{T_{12}}}&{{T_{22}}}&{{T_{32}}} \\ {{T_{13}}}&{{T_{23}}}&{{T_{33}}} \end{array}} \right]$ | (14) |
由式(13)和(14)得:
| $\left\{ \begin{aligned} & \theta = \arcsin \left( {{T_{32}}} \right) \\ & \phi = \arctan \left( { - \frac{{{T_{31}}}}{{{T_{33}}}}} \right) \\ & \psi = \arctan \left( {\frac{{{T_{12}}}}{{{T_{22}}}}} \right) \end{aligned} \right.$ | (15) |
由式(14)和式(15)通过上述公式变换即可解算出载体的姿态角得出:
| $\left\{ {\begin{aligned} & {\theta = \arcsin \left( {2 \cdot \left( {{q_2} \cdot {q_3} + {q_0} \cdot {q_1}} \right)} \right)} \\ & {\phi = \arctan \left( { - \frac{{2 \cdot \left( {{q_1} \cdot {q_3} + {q_0} \cdot {q_2}} \right)}}{{1 - 2 \cdot \left( {q_1^2 + q_2^2} \right)}}} \right)} \\ & {\psi = \arctan \cdot \left( {\frac{{2 \cdot \left( {{q_1} \cdot {q_2} - {q_0} \cdot {q_3}} \right)}}{{1 - 2 \cdot \left( {q_1^2 + q_3^2} \right)}}} \right)} \end{aligned}} \right. $ | (16) |
设三轴加速度计和三轴磁力计在静止条件下的初始姿态角为(
| $\left\{ {\begin{aligned} & {q_0^2 + q_1^2 - q_2^2 + q_3^2 = {T_{11}}} \\ &{q_0^2 - q_1^2 + q_2^2 - q_3^2 = {T_{22}}} \\ & {q_0^2 - q_1^2 - q_2^2 + q_3^2 = {T_{33}}} \\ & {q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1} \end{aligned}} \right.$ | (17) |
由式(13)和式(17)可得:
| $\left\{ {\begin{aligned} & {{q_1} = \pm \frac{1}{2}\sqrt {1 + {T_{11}} + {T_{22}} + {T_{33}}} } \\ & {{q_1} = \pm \frac{1}{2}\sqrt {1 + {T_{11}} - {T_{22}} - {T_{33}}} } \\ & {{q_2} = \pm \frac{1}{2}\sqrt {1 - {T_{11}} + {T_{22}} - {T_{33}}} } \\ & {{q_3} = \pm \frac{1}{2}\sqrt {1 - {T_{11}} - {T_{22}} + {T_{33}}} } \end{aligned}} \right.$ | (18) |
由式(18)即可得出初始四元数.
3.1.5 更新四元数四元数的更新常采用一阶龙格-库塔法算法来实现[3], 一阶龙格-库塔法的解为:
| $Q[t + \Delta t] = Q[t] + \Delta t\frac{{{\rm{d}}Q}}{{{\rm{d}}t}}$ | (19) |
进而可推出:
| ${\left[ {\begin{array}{*{20}{l}} {{q_0}} \\ {{q_1}} \\ {{q_2}} \\ {{q_3}} \end{array}} \right]_{t + \Delta t}} = {\left[ {\begin{array}{*{20}{l}} {{q_0}} \\ {{q_1}} \\ {{q_2}} \\ {{q_3}} \end{array}} \right]_t} + \frac{{\Delta t}}{2}\left[ {\begin{array}{*{20}{r}} { - {w_x}{q_1} - {w_y}{q_2} - {w_z}{q_3}} \\ {{w_x}{q_0} + {q_2} - {w_y}{q_3}} \\ {{w_y}{q_0} - {w_z}{q_1} - {w_x}{q_3}} \\ {{w_z}{q_0} + {w_y}{q_1} - {w_x}{q_2}} \end{array}} \right]$ | (20) |
设
| $\left\{ {\begin{array}{*{20}{l}} {{q_0} = {q_0} + ( - {q_1}*{g_x} - {q_2}*{g_y} - {q_3}*{g_z})*{T / 2}} \\ {{q_1} = {q_1} + ({q_0}*{g_x} + {q_2}*{g_z} - {q_3}*{g_y})*{T / 2}} \\ {{q_2} = {q_2} + ({q_0}*{g_y} - {q_1}*{g_z} + {q_3}*{g_x})*{T / 2}} \\ {{q_3} = {q_3} + ({q_0}*{g_z} + {q_1}*{g_y} - {q_2}*{g_x})*{T / 2}} \end{array}} \right.$ | (21) |
计算当前时刻的四元数Q (t+T), 并对其进行归一化处理:
| $Q(t + T) = \frac{{Q(t + T)}}{{\left\| {Q(t + T)} \right\|}}$ | (22) |
设四元数
| $mode = \sqrt {q_0^2 + q_1^2 + q_2^2 + q_3^2}$ | (23) |
| $\left\{ {\begin{array}{*{20}{l}} {{q_0} = {{{q_0}} / {mode}}} \\ {{q_1} = {{{q_1}} / {mode}}} \\ {{q_2} = {{{q_2}} / {mode}}} \\ {{q_3} = {{{q_3}} / {mode}}} \end{array}} \right.$ | (24) |
由式(24)可得姿态角为:
| $\left\{ \begin{aligned} & \psi = \arcsin (2 \cdot ({q_2} \cdot {q_3} + {q_0} \cdot {q_1})) \\ & \theta = \arctan \left( { - \frac{{2 \cdot ({q_1} \cdot {q_3} - {q_0} \cdot {q_2})}}{{1 - 2 \cdot (q_1^2 + q_2^2)}}} \right) \\ & \phi = \arctan \left( {\frac{{2 \cdot ({q_1} \cdot {q_2} - {q_0} \cdot {q_3})}}{{1 - 2 \cdot (q_1^2 + q_3^2)}}} \right) \end{aligned} \right.$ | (25) |
作为一种高效的自回归滤波器, 卡尔曼滤波常用于解决离散的线性系统滤波问题. 卡尔曼滤波通过最小均方差来衡量最佳估计的标准, 算法的实现是通过求解状态方程和观测方程然后不断的更新最小均方差, 进而得出最优估计.
3.2.1 状态方程和观测方程一个常规的线性离散系统模型, 其状态空间方程如式(26)所示:
| ${x_k} = {F_{k - 1}}{x_{k - 1}} + {G_{k - 1}}{u_{k - 1}} + {w_{k - 1}}$ | (26) |
其中,
观测方程如下:
| ${z_k} = H{x_k} + {v_k}$ | (27) |
其中,
状态方程中的噪声w和测量噪声v默认情况下认为两者是相互独立且满足高斯分布的白噪声, 即:
| $p(w)\sim N(0,Q)$ | (28) |
| $p(v)\sim N(0,R)$ | (29) |
为了在实际使用中简化算法, 常假设噪声协方差矩阵Q和测量噪声协方差矩阵R均为定值.
3.2.2 卡尔曼滤波算法流程卡尔曼滤波算法在数学方法中是一种递归预测法, 以偏差的最小方差为标准, 计算得到系统的最优估计值, 具有较好的实时性和抗干扰性[4]. 卡尔曼滤波算法是通过测量过程和预测过程间的相互更新相互反馈并通过求解卡尔曼增益和更新状态方程来实现系统的自回归状态估计, 进而求出系统的最优估计. 卡尔曼滤波器可分为时间更新方程和测量更新方程.
式(30)和式(31)为卡尔曼时间更新方程:
| ${\hat x_{\bar k}} = {A_{{{\hat x}_{k - 1}}}} + B{u_{k - 1}}$ | (30) |
| ${P_{\bar k}} = A{P_{k - 1}}{A^{\rm{T}}} + Q$ | (31) |
时间更新方程中,
式(33)和式(34)为状态更新方程:
| $K = {P_{\bar k}}{H^{\rm{T}}}{(H{P_{\bar k}}{H^{\rm{T}}} + R)^{ - 1}},$ | (32) |
| ${\hat x_k} = {\hat x_{\bar k}} + K\{ {z_k} - H{x_{\bar k}}\} ,$ | (33) |
| ${P_k} = (I - KH){P_{\bar k}}.$ | (34) |
状态更新方程中, K为滤波增益矩阵即卡尔曼增益,
由于三轴陀螺仪是通过角速度的积分获得姿态角, 存在随机漂移误差和常值误差, 随着时间的增加, 必然会使输出误差也积累增加, 因此单独使用陀螺仪进行姿态解算无法获得准确的姿态角. 加速度计只有在静止或匀速状态下通过测量重力场, 可以准确计算出姿态角, 但是在实际情况中加速度计通常处于动态环境中, 因此单独使用加速度计解算出的姿态角同样不可靠. 由于外界磁场的干扰, 单独使用磁强计计算出的偏航角同样存在误差. 为解决上述问题, 很多控制领域的专家做了大量研究, 并提出多种组合测量的方案[5], 结合本文需求及精确度要求, 本文结合卡尔曼滤波的递归预估特性, 采用一种基于卡尔曼滤波的数据融合算法.
3.3.1 状态方程的建立状态方程的建立是将陀螺仪输出的角速度通过四元数微分方程计算姿态角的过程, 作为当前状态的预测. 通过四元数微分方程求出的姿态角, 将作为当前预测值. 姿态角的详细计算过程已经在3.1节四元数姿态解算中详细叙述, 所以这里只给出相关公式:
四元数微分方程:
| $Q = \frac{1}{2}Q \cdot \omega $ | (35) |
其中, ω为沿坐标系的角速度.
将式(35)展开:
| $\left[ {\begin{array}{*{20}{l}} {{q_0}} \\ {{q_1}} \\ {{q_2}} \\ {{q_3}} \end{array}} \right] = \frac{1}{2} \cdot \left[ {\begin{array}{*{20}{c}} 0&{ - \omega x}&{ - \omega y}&{ - \omega z} \\ {\omega x}&0&{\omega z}&{ - \omega y} \\ {\omega y}&{ - \omega z}&0&{\omega x} \\ {\omega z}&{\omega y}&{ - \omega x}&0 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{q_0}} \\ {{q_1}} \\ {{q_2}} \\ {{q_3}} \end{array}} \right]$ | (36) |
通过四元数归一化可求出当前时刻姿态角(俯仰角、翻滚角、偏航角).
由卡尔曼滤波经典状态方程可知预测值包含真实角度和误差角度, 所以这里我们将所求的姿态角作为真实角度和误差角度的合成, 用公式可表示为:
| $\phi _G^k = \phi _T^k + \Delta \phi _G^k.$ | (37) |
其中,
将由加速度计和磁力计测量出的实际姿态角作为观测量.
假设通过加速度计和磁力计计算出的姿态角为
| $\theta _{AM}^k = \theta _T^k + \Delta \theta _{AM}^k$ | (38) |
其中,
在实际卡尔曼滤波器应用过程中, 过程噪声协方差Q, 即作为预测姿态角的陀螺仪获取姿态角的过程误差协方差矩阵, 通常不容易得到, 但可以通过实验的方法计算得到. 测量噪声协方差R, 即作为测量姿态角的加速度计和磁力计的噪声协方差矩阵, 通过分析得到包含测量噪声的数据, 测量噪声协方差R可以通过数据的融合更新得到, 具体计算过程如下:
由前节的介绍可知: 陀螺仪角度的估计误差为
| ${\Delta _G} =\phi _G^{k + 1} - \phi_G^k = (\phi_T^{k + 1} - \phi _T^k) + (\Delta \phi_G^{k + 1} - \Delta \phi_G^k)$ | (39) |
| ${\Delta _{AM}} = \theta _{AM}^{k + 1} - \theta _{AM}^k = (\theta _T^{k + 1} - \theta _T^k) + (\Delta \theta _{AM}^{k + 1} - \Delta \theta _{AM}^k)$ | (40) |
将上面两式相减, 即可得到两时刻的融合误差:
| $ f = {\Delta _{AM}} - {\Delta _G} = (\Delta \theta _{AM}^{k + 1} - \Delta \theta _{AM}^k) - (\Delta \phi _G^{k + 1} - \Delta \phi _G^k) $ | (41) |
求融合误差协方差:
| $\operatorname{cov} (f,f) = E[(f - Ef)(f - Ef)]$ | (42) |
由于陀螺仪、加速度计和磁力计的误差为相互独立, 即自相关性为0, 满足:
| $E[\Delta \phi _G^{k + 1} \cdot \Delta \phi_G^k] = 0,E[\Delta \theta _{AM}^{k + 1} \cdot \Delta \theta _{AM}^k] = 0$ | (43) |
则由式(41)~式(43)经过化简及近似取代可得误差协方差的最终结果为:
| $\operatorname{cov} (f,f) = 2E\left[ {{{(\Delta \theta _{AM}^k)}^2}} \right]$ | (44) |
则得加速度计和磁力计的协方差R:
| $R = 1/2\operatorname{cov} (f,f) = E\left[ {{{(\Delta \theta _{AM}^k)}^2}} \right]$ | (45) |
通过以上计算得出的测量噪声协方差R, 用于卡尔曼滤波的自回归数据更新, 经过反复优化迭代, 进而得到最优姿态角.
3.3.4 算法流程(1)初始化参数, 记初始状态k=1, 在六轴MPU6050传感器处于静止状态下, 通过陀螺仪、加速度计和磁力计获取初始角度.
(2)当k=2时, 根据陀螺仪的角速度数据, 通过四元数法进行姿态解算预测当前角度, 根据前期陀螺仪数据实验求得先验误差协方差
(3)按照式(32)求出卡尔曼增益K.
(4)根据k=2时刻的加速度计和磁力计求出的姿态角作为观测值, 按式(33), 式(34)实现预测值更新.
(5)计算k+1时刻的预测值. 实现方法: 通过采集k+1时刻的陀螺仪输出的角速度, 代入四元数微分方程求出此时刻的姿态角, 并作为预测值. 然后循环执行步骤(3)和步骤(4).
算法流程如图5所示, 先对初始时刻采集的陀螺仪、加速度计和磁力计原始数据进行相应的滤波处理, 若是初始状态下, 那么将陀螺仪和加速度计解算出的姿态角作为初始姿态角, 并根据初始姿态角求出初始四元数, 然后将通过陀螺仪采集到的数据带入四元数微分方程进而求出姿态角, 并作为估计角度, 通过采集加速度计和磁力计数据并通过计算求出的姿态角作为测量值, 可计算出过程噪声协方差和测量噪声协方差. 利用卡尔曼滤波算法将预测角度和测量角度进行融合得到最优估计角度, 由卡尔曼滤波公式可知, 两个符合高斯分布的数据融合后仍然满足高斯分布且最优值处在融合后的高斯分布曲线, 因此可将每次计算出的姿态角作为下次融合的初始角, 反复的数据融合能够得到一系列稳定的最优估计角度[7].
3.3.5 卡尔曼滤波数据融合算法的适用性本文通过卡尔曼滤波数据融合算法输出姿态角, 而实际系统中总是存在不同程度的非线性因素, 利用线性化卡尔曼滤波方法, 通过不断地统计和计算数据方差来自动改变卡尔曼增益系数K, 因此当系统存在噪声或者预测量的累积误差较大时, 也能提高系统精度, 误差能够通过快速迭代而减少.
智能钓鱼竿中采用高性能单片机获取高频的姿态数据, 自动整定得到的卡尔曼增益系数具有较强的通用性, 同时计算量相对较大. 智能钓鱼竿系统中使用的STM32微处理器能够保证数据融合线程周期不超过100 ms, 较高的姿态融合频率可以保证预测量误差较小且收敛速度较快, 因而基于线性卡尔曼滤波的姿态数据融合能较好地完成对目标的滤波估计处理.

|
图 5 算法流程图 |
3.4 基于PID控制算法的智能遛鱼控制方案
本文中所述鱼竿是以电机转动带动鱼竿纺线轮实现鱼线自动收放线的智能钓鱼竿. 所谓遛鱼, 指的是一种钓鱼方法. 钓鱼时如果钓到个体较大的鱼一般都不能直接将鱼提上来, 鱼势必在被勾住后挣扎逃窜, 此时我们需要根据鱼的力气大小来选择收线和放线, 在收线和放线的来回拉扯中, 逐渐消耗掉鱼的体力, 当鱼精疲力竭停止反抗时, 将鱼拉回岸边的这个过程, 形象地称为“遛鱼”.
通过上文中的姿态解算及卡尔曼滤波数据融合可得鱼竿的实时姿态角, 结合图6对鱼竿模型进行分析: 当检测到鱼竿的俯仰角的倾角偏差大于或等于

|
图 6 鱼竿倾角示意图 |
3.4.1 串级PID控制模型的建立
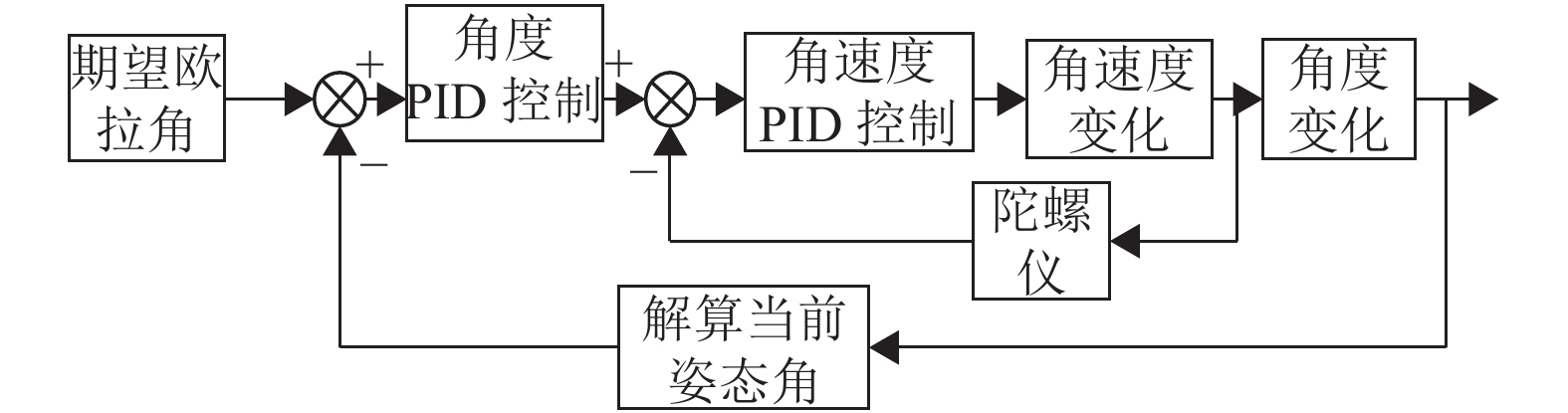
本文采用双环PID控制系统, 即外环采用角度环, 内环采用角速度环, 角速度环的加入将更加准确的表示鱼竿姿态, 使控制系统更加稳定. 与传统的单环PID控制器相比, 增强了控制系统对外界的抗干扰能力, 提高了控制精度. 智能钓鱼竿串级PID控制流程图如图7所示.
3.4.2 串级PID控制系统Simulink仿真本文中采用以角度作为外环控制, 角速度作为内环控制的串级PID与以角度作为控制量的单环PID控制作比较. 从而验证串级PID控制的优越性. 在该系统仿真中输入量为指定的角度, 输出为经过串级PID控制输出的角度, 该系统将以阶跃信号为输入进行系统仿真, 通过参考飞行器的数学模型的推导, 在这里假设该俯仰角、翻滚角及偏航角的传递函数分别为:
| $\left\{ {\begin{aligned} & {G1(s) = \frac{{38.5}}{{0.1{s^2} + 1}}} \\ & {G2(s) = \frac{{38.5}}{{0.1{s^2} + 1}}} \\ & {G3(s) = \frac{{48.6}}{{0.1{s^2} + 1}}} \end{aligned}} \right.$ | (46) |
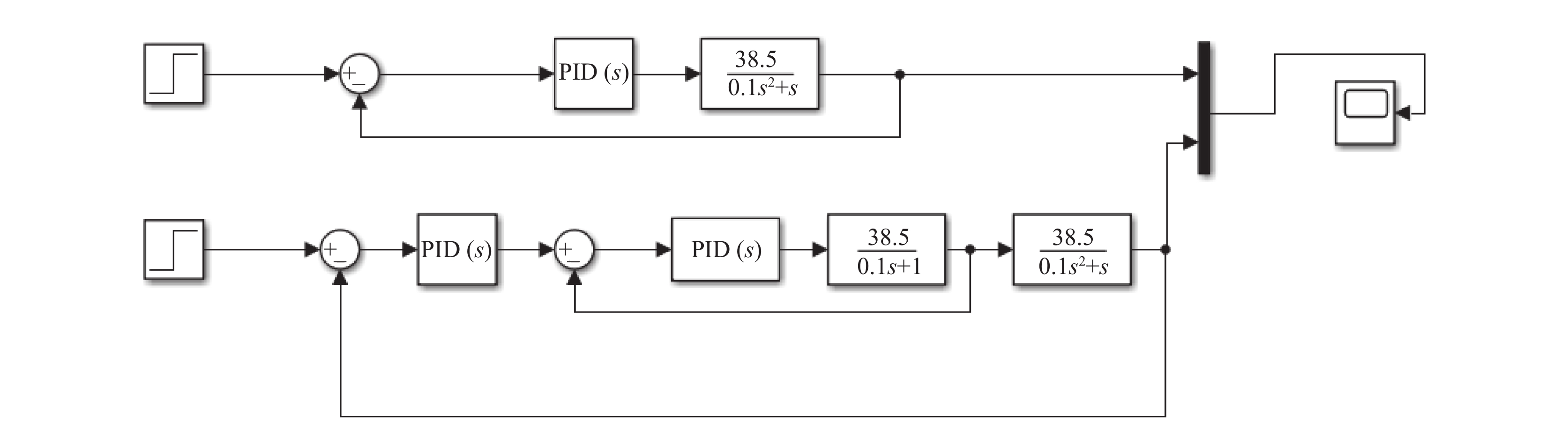
可建立单级和串级PID下俯仰角和翻滚角Simulink仿真结构如图8.
|
图 7 串级PID控制流程图 |
|
图 8 单级和串级PID下俯仰角和翻滚角仿真结构图 |
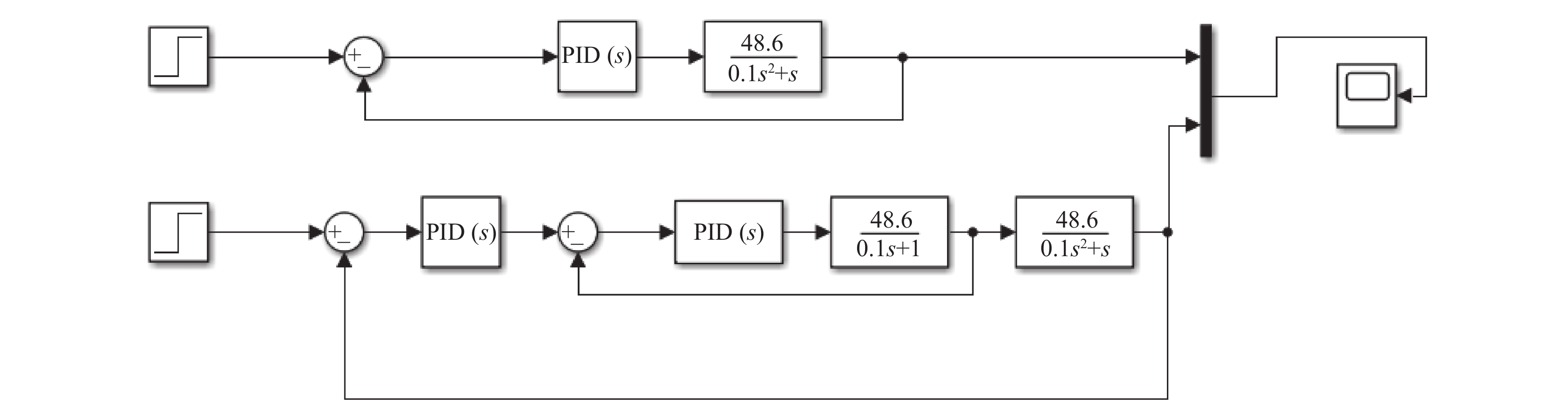
可建立单级和串级PID下偏航角Simulink仿真结构如图9.
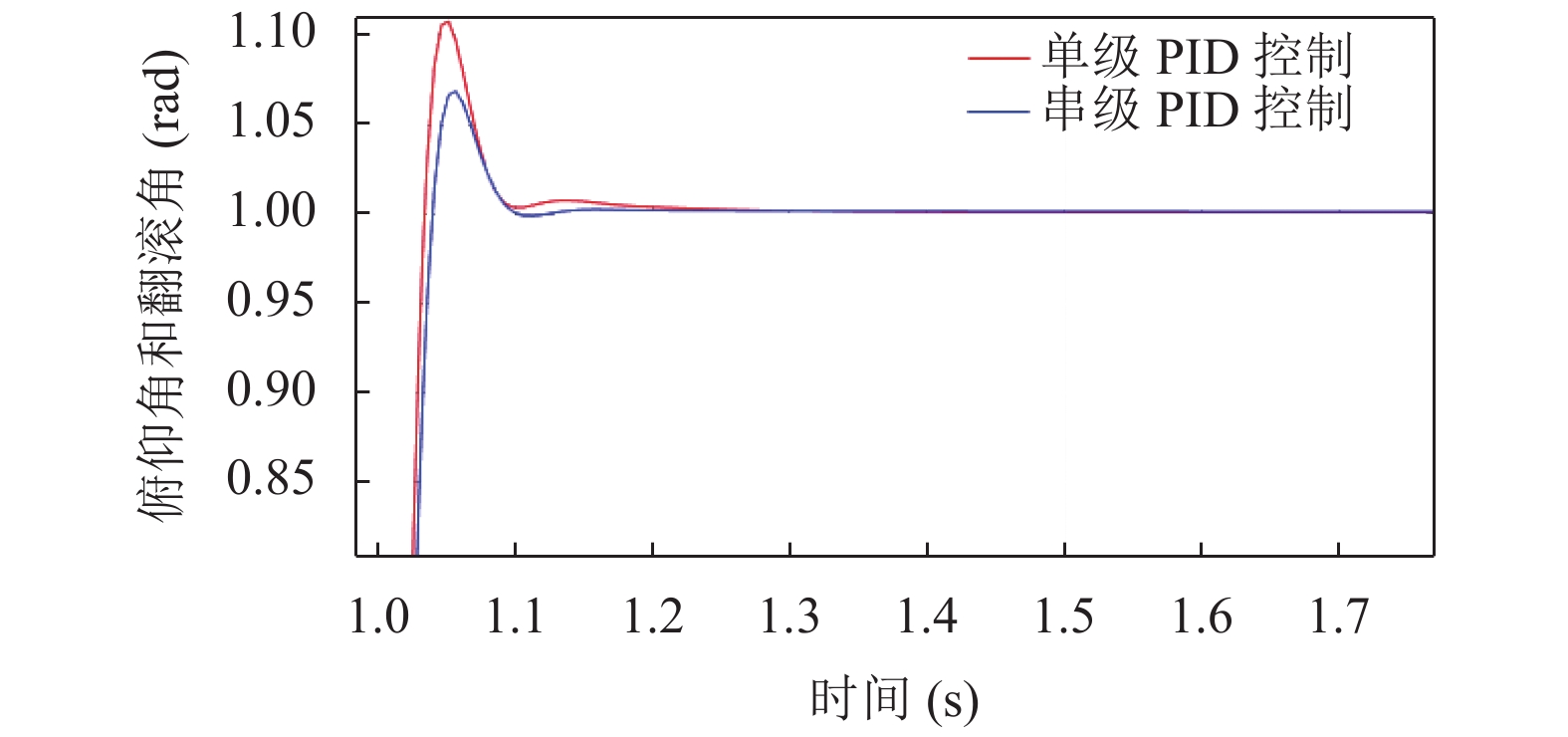
俯仰角、翻滚角的单极与串级PID仿真结果对比如图10所示, 图中红线为单级PID仿真波形, 蓝线为串级PID仿真波形:
偏航角的单极与串级PID仿真结果对比如图11所示.
由图10和图11仿真结果图可见, 在输入信号为阶跃信号的控制系统中, 单极PID控制下系统的超调量和振荡次数明显大于串级PID控制下系统的作用, 因此串级PID控制系统下控制信号更稳定且响应速度更快.
3.4.3 PID参数整定本节采用试凑法对串级PID参数进行整定. 试凑法是根据以往经验依照先内环、后外环、先比例、后积分再微分的步骤来实现参数整定. 由于参数整定过程类似, 本节以俯仰角为例进行调试.
首先整定内环PID参数, 比例参数Kp=4时, 此时系统振荡剧烈, 系统严重超调, 此时应减小Kp的值. Kp=1时系统需要很长时间才能恢复到1值, 说明Kp值偏小, 因此可初步判断Kp=3时较为合适. 但是单纯的比例调节无法使系统快速稳定, 还应加入积分调节, 调节依据是若系统误差消除较慢, 此时应当适当减少积分时间, 增强积分作用. 此时系统可以较快的消除误差, 但系统超调量较大, 此时应加入微分作用减少超调量, 加入微分控制量能一定程度上抑制超调量.
|
图 9 单级和串级PID下偏航角仿真结构图 |
|
图 10 俯仰角和翻滚角仿真结果对比图 |

|
图 11 偏航角仿真结果对比图 |
由于PID参数的调试是一个参数间相互耦合的过程, 所以在调试中要不断的尝试和试凑才能得出最终理想的参数. 通过反复试凑的方法, 最终确定智能鱼竿PID控制参数如表1所示, 最终俯仰角的PID仿真结果图如图12所示.
由最终的串级PID仿真图, 可知系统在阶跃信号输入的控制系统中, 响应时间约为0.03 s, 系统稳定时间约为0.1 s且系统超调量在10%以内, 因此该串级PID控制系统能够快速响应并快速趋于稳定, 能较好地实现鱼竿的控制需求.
| 表 1 智能鱼竿PID控制参数表 |

|
图 12 俯仰角PID最终仿真结果图 |
4 智能钓鱼竿系统测试结果
智能钓鱼竿系统实物图如图13所示, 考虑到鱼竿对轻便的需求, 经过调试, 实现了智能钓鱼竿的相关基本功能, 如智能报警功能. 该智能钓鱼竿设计成本低廉且功能实用, 具有较好的实用价值和广阔的市场前景.
4.1 姿态角测试结果由姿态传感器数据处理得到精确的姿态角是控制系统的基础, 其测量结果的准确性对于实验结果准确性有很大的影响.
由于陀螺仪和加速度计均存在不同频段的噪声而导致在检测过程中产生一定的误差, 所以本系统采用了卡尔曼数据融合方式来降低误差, 图14为传感器静止时, 最终解算出的欧拉角波形.

|
图 13 智能钓鱼竿整体实物图 |
|
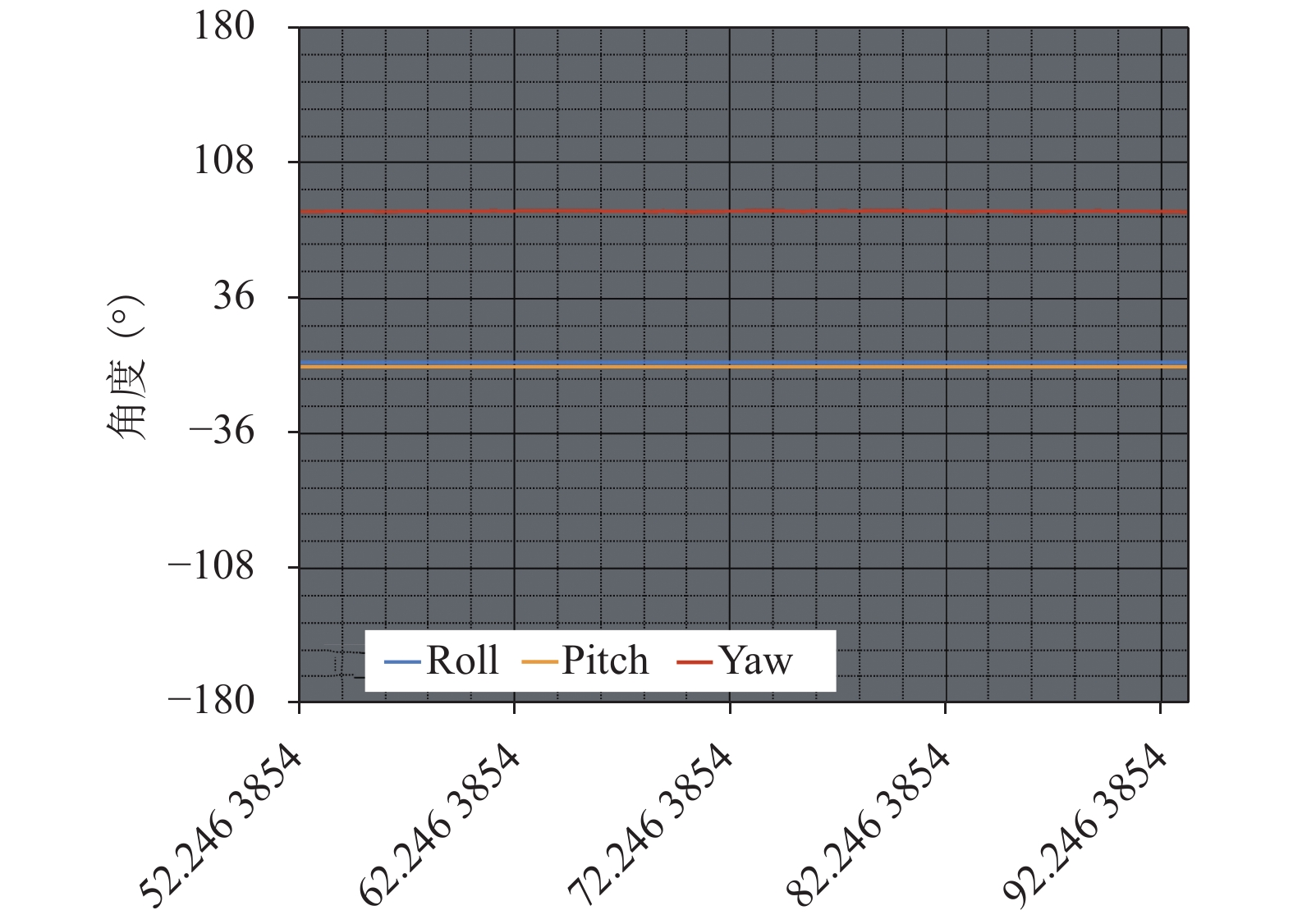
图 14 静止时解算的姿态角波形图 |
由图14可知, 蓝色曲线表示翻滚角, 黄色曲线表示俯仰角, 红色曲线表示航向角, 传感器水平静止放置时, 姿态角的初始值曲线相对平滑且俯仰角和翻滚角角度均接近零, 说明本文中通过卡尔曼数据融合算法最终得出的姿态角相对精确且噪声较小.
图15为智能钓鱼竿实际运行时姿态角变化波形图, 航向角的量程范围为–180°到+180, 则从–180°变化到+180°时, 角度会突变. 由图可知在7–8 s的时间段内Yaw出现了从–180°到+180°的突变, 因此在智能钓鱼竿姿态控制时会对该处进行平滑处理.

|
图 15 角度突变时解算的姿态角波形图 |
4.2 智能鱼竿报警功能测试
智能鱼竿的报警是依据俯仰角的变化作为咬钩信号的判断, 当鱼竿俯仰角的变化在10度以上时, 则认为此时有鱼咬钩, 且可以通过调节报警阈值来改变智能钓鱼竿报警的灵敏度. 对测试数据进行统计得出表2.
分析表2可知, 当翻滚角和偏航角保持不变时, 俯仰角度变化大于10度时鱼竿报警, 俯仰角变化小于10度时, 鱼竿不报警, 当俯仰角度不发生变化时, 无论翻滚角和偏航角如何变化, 鱼竿均不报警, 且由表中数据分析可知鱼竿倾角变化在较接近10度时依然可以很准确的发出报警信号, 这也从侧面证明姿态解算出的姿态角精度较高.
| 表 2 鱼竿报警数据分析表 |
5 结论与展望
本文以微处理器STM32为核心搭建uC/OS-II操作系统, 通过四元数法对鱼竿姿态解算, 提出基于卡尔曼滤波的数据融合算法, 并以串级PID控制算法实现了鱼竿控制系统的智能控制, 并通过Matlab建立Simulink仿真, 验证了串级PID控制器的有效性. 通过实验测试最终达到了本设计的预期功能.
| [1] |
张荣辉, 贾宏光, 陈涛, 等. 基于四元数法的捷联式惯性导航系统的姿态解算. 光学 精密工程, 2008, 16(10): 1963-1970. |
| [2] |
姚佳乐, 沈宏君, 张虹波. 变桨距四旋翼飞行器控制系统设计. 微型机与应用, 2017, 36(6): 77-79, 83. |
| [3] |
刘志军, 吕强, 王东来. 小型四旋翼直升机的建模与仿真控制. 计算机仿真, 2010, 27(7): 18-20, 69. DOI:10.3969/j.issn.1006-9348.2010.07.005 |
| [4] |
许震, 毛丽民, 刘同连, 等. 四轴飞行器控制系统设计. 常熟理工学院学报, 2013, 27(2): 109-113. DOI:10.3969/j.issn.1008-2794.2013.02.024 |
| [5] |
吴明洋. 主动雷达目标状态估计算法研究[硕士学位论文]. 上海: 上海交通大学, 2012.
|
| [6] |
邹波, 张华, 姜军. 多传感信息融合的改进扩展卡尔曼滤波定姿. 计算机应用研究, 2014, 31(4): 1035-1038, 1042. DOI:10.3969/j.issn.1001-3695.2014.04.019 |
| [7] |
陈伟. 基于四元数和卡尔曼滤波的姿态角估计算法研究与应用[硕士学位论文]. 秦皇岛: 燕山大学, 2015.
|
 2020, Vol. 29
2020, Vol. 29


