随着计算机技术的发展, 数据挖掘技术在现实生活中的作用也越来越大. 与此同时, 类似各类传感器、股票交易、境污染监控、通信传输等各个领域中的数据量有了爆发式的增长. 这种海量的数据有维度高、实时性强、变化快和延伸性好的特点. 如果按照传统的聚类方法, 先收集数据再进行聚类处理已不适合于大规模的数据. 传统的聚类算法适用于对有限的数据进行聚类分析, 而面对源源不断的数据难以进行存贮处理, 并且也具有很高的时间复杂度[1]. 可见, 数据流聚类分析是当下和未来数据挖掘中的一个研究热点.
关于数据流聚类算法理论, 先后出现了传统的BIRCH算法、STREAM算法、CluStream算法、HPStream算法、DenStream算法和D-Stream算法, 而2003年Aggarwal C等提出的以界标窗口聚类分析算法为代表的CluStream算法[2]成为数据流聚类算法研究过程中的重要转折点, 标志着增量式处理方式的聚类算法自此出现. 虽然该算法在很多实际工程中都得到了应用, 但对变速的数据流处理却有一定的劣势. 2015年陈顺生等对基于对数据时间点以及速度的占比因素的考虑, 提出了一种动态可调滑动窗口数据流聚类算法DWSWC[3]. 该算法发现并记录了数据流流速与窗口大小之间的关系, 同时为了减少窗口变化的次数, 引入调节因子参数和变异数据流聚类结构, 提高了数据特征属性对聚类结果的影响. 但该算法过于注重在线微聚类结果, 离线处理较为简单, 降低了聚类质量. 2018年Fahy C等提出一种基于密度聚类的蚁群数据流聚类算法[4], 将聚类定义为特征空间由低密度区域分割的高密度区域. 人工蚂蚁根据局部密度和局部相似度, 通过概率选取和丢弃微簇来对簇进行分类, 提高了聚类质量和可扩展性. 2011年肖裕权等提出一种基于群体协作的粒子群优化算法的数据流聚类算法CluPSO[5]. 通过指数直方图和粒子群算法对用户数据进行聚类分析, 减少了数据信息的缺失, 提高了聚类的准确性. 但是忽略了阈值T对于整体聚类效果的影响.
类似于粒子群算法的智能优化算法可以在离线部分发挥该类算法的优势, 通过动态迭代来优化聚类结果. 因此本文提出了一种基于人工蜂群优化的数据流聚类算法. 通过在线部分动态滑动窗口和改进的初始化阈值半径T, 将连续数据生成聚类效果更好的微簇; 在离线部分中采用改进的人工蜂群算法来改善聚类性能. 整体上提高了聚类质量.
1 相关概念 1.1 动态滑动窗口模型滑动窗口模型是指在不同的时刻, 根据窗口的滑动来处理不同的数据, 滑动窗口处理最后一个数据的时刻则是当前的最新时刻. 一般来说, 可以通过时间范围和窗口内的数据量来定义窗口大小. 滑动窗口自左向右的数据流传输方向, 如图1所示.

|
图 1 滑动窗口模型 |
本文算法根据数据流速度不断变化的实际情况引入了一种动态滑动窗口[6]来满足内存最大的使用率以及数据的最大贡献率. 通过将数据进入滑动窗口的时间以及流出滑动窗口的时间添加到微聚类特征中, 来提高时间属性对聚类产生的影响.
滑动窗口由静态固定大小W和动态可调节大小
在数据流速度为匀速时, 滑动窗口大小保持为W不变. 而在实际数据流传输的过程中, 每个数据项进入滑动窗口的实际时间为RE, 离开滑动窗口的时间是RL. 即数据在数据流窗口内停留的时间为
(1)在数据传送速度较慢时, 实际的数据流速度
(2)在数据流的传送过程中实际速度
(3)在数据流的传送过程中实际的速度
借鉴层次聚类中的聚类特征, 将数据流中的各个数据属性添加到微簇中. 定义微簇在数据样本中为
聚类过程中采用的距离公式如式(1), 式(2).
样本点到聚类中心的距离, 如式(1):
| $ Dis({X_a},C{F_b}) = \sqrt {\sum\limits_{i = 1}^d {{{\left(X_a^i - \frac{{F_b^i}}{n}\right)}^2}} } $ | (1) |
式中,
聚类中心之间的距离, 如式(2):
| $Dis(C{F_a},C{F_b}) = \sqrt {\sum\limits_{j = 1}^d {{{\left(\frac{{F_a^j}}{n} - \frac{{F_b^j}}{n}\right)}^2}} } $ | (2) |
式中,
在处理大规模的数据时, 借鉴Birch算法CF树中第一阶段中的阈值T的概念. 由于微聚类是将源源不断到来的数据通过存储属性特征进行压缩储存, 这样极大地节省了内存空间. 微簇半径是通过类内平均距离或类间平均距离计算的, 因此阈值半径的取值直接影响了数据分布. 所以提出一种阈值半径取值方法, 步骤如下:
(1)通过随机抽样的方法在样本数据集中选取适中规模的数据;
(2)对抽样样本两两随机为N对, 并计算每对数据间的距离;
(3)计算N对数据间的距离的期望EX和方差DX;
(4)构建阈值半径T, T=P×(EX+0.25×DX); 其中P通过统计得出取1/3时效果最优.
2 离线部分的数据流聚类优化 2.1 人工蜂群聚类优化算法思想本文在离线部分处理在线部分产生的微簇时, 将K-means算法与改进的蜂群算法相结合通过迭代计算得出最优聚类结果. 该算法的优势是采用了迭代记忆机制的方法.
2.2 基本人工蜂群算法人工蜂群算法是Karaboga D[7]提出的一种类似于粒子群算法的优化算法, 它的基本思想受启发于蜜蜂可以在不接受外界因素的情况下通过不同的分工合作和信息共享找到最丰富的蜜源. 人工蜂群对于求解约束优化问题有着天然的优势, 相比于经典算法来说更容易找到全局最优解. 通过与其他优化算法相比较发现, 人工蜂群算法具有参数少, 判断进化条件单一, 探索能力强的优点.
2.3 改进的人工蜂群算法(1)最大最小距离初始化
对于人工蜂群算法来说, 种群的初始化对求解的质量和收敛的速度有很大的影响. 随机性较强的初始化会造成局部收敛能力较弱, 影响全局收敛速度. 所以针对这个缺点, 本文参考文献[8,9]引入一种最大最小距离积法来解决初始化随机性较高的问题. 通过该方法, 初始点在选择时能够更有针对性的选择数据分布密度大的数据点, 并且增大了初始点的分散度; 在此过程中也可以利用乘积的方式进一步扩大数据间的差异, 减少了算法迭代次数, 提高了收敛速度和精准度.
(2)适应度函数
不同的适应度函数决定着不同的种群求解方向, 结合人工蜂群计算中的迭代过程采用一种适应度函数, 如式(3):
| $fi{t_i} = \frac{{C{N_i}}}{{{J_i}}};i = 1,2,\cdots ,N$ | (3) |
其中,
(3)位置更新公式
人工蜂群虽然有良好的全局探索性能, 但开发能力不足, 位置更新速度较慢. 对于种群进化来说, 每个个体都应享有整个种群提供的信息. 而人工蜂群算法在寻找蜜源过程中没有考虑到迭代前后的位置比较, 只能将当前位置信息与历史最佳位置信息比较, 缺乏对全局最优位置的考虑. 针对这个缺点引入一种带有调节因子的位置更新式(4), 该公式通过加入调节因子来不断调节位置更新幅度. 若当前所在位置与历史最佳位置相差较大, 则会增加更新幅度, 反之则会降低更新幅度.
| ${v_{id}} = {x_{id}} + \varphi ({x_{md}} - {x_{kd}}) + \theta ({x_{{\rm{best}},d}} - {x_{id}})$ | (4) |
其中,
| ${P_i} = \frac{{fi{t_i}}}{{\displaystyle\sum\limits_{i = 1}^N {fi{t_i}} }};\;\;i = 1,2,\cdots,N$ | (5) |
其中,
在线微聚类是建立在动态滑动窗口的基础上, 利用Birch算法中的CF树概念, 将数据样本按照数据属性特征逐步聚类成适当规模数量的微簇.
在线部分程序伪代码如下:
输入: 数据集样本D, 时间调节因子
输出: 通过动态滑动窗口生成K个微簇CF.
初始化微簇数量K=0
For数据集D的每个
For初始每个聚类特征
根据式(1)计算
If(
If(num>UB)
then{根据式(2)将距离最近的两个微簇合并; K←(K+1)}
Else{以
Else{根据式(1)把
If(
then {
Else if(
then {
Else {
End For
End For
3.2 离线算法(1)对微簇集初始化并进行K-means计算得到聚类中心. (2)通过改进的蜂群算法对聚类中心进行迭代计算得到新的聚类中心并更新蜂群. (3)将K-means算法与改进的蜂群算法交替计算, 在最大迭代次数内求出最优聚类结果.
离线部分程序伪代码如下:
输入: 种群规模CZ(引领蜂与跟随蜂数量均为种群规模的1/2); 蜜蜂最大迭代次数maxCycle; 蜜源被开发最大限制次数Limit; 初始化迭代次数Cycle=0, 限制次数iter=0.
输出: CZ/2个簇.
初始化CF得到
DO K-means
计算 fit(
While(Cycle<=maxCycle) do
{Initialize(
计算 Maxfit(
Prob(
While(i<CZ/2) do
{If(
then { Initialize (
计算 Maxfit(
i←i+1}
If(iter>Limit)
then { Initialize (
Else {iter←(iter+1)}
对邻域搜索到的点进行一次K-means聚类, 更新蜂群.
Cycle←(Cycle+1)}
Output聚类中心
3.3 算法分析在线部分: 将源源不断到来的数据转化为内含有特征属性的微簇, 通过一次处理但并不保留数据的方式, 极大地节省了存储空间, 降低了空间复杂度. 在线部分对于数据不需要过于细致的处理, 但对于微聚类效率要求更高.
离线部分: 将在线部分产生的微簇通过改进的蜂群算法进行处理得到CZ/2个簇. 该算法对于时间效率要求不高, 对聚类的质量有较高的要求.
4 实验分析 4.1 实验数据与参数设置为了验证本文算法的有效性, 本文数据集将采用KDD-CUP-99入侵检测数据集来进行算法测试. 该数据集是由模拟美空军局域网历经两个多月的时间所收集的网络连接数据汇集而成, 在很多文献中也都有所引用. 据统计, KDD-CUP-99测试数据集涵盖4.94×105条连接记录, 每一条连接记录是由41个特征属性和一个决策类属性构成; 41个特征属性包括9个离散型属性、32个连续型属性[10]. 该数据集具有数量大、类别多的特点, 经常被学术界运用于检测数据流聚类算法性能和精度. 在检测数据流聚类的聚类效果时, 常将聚类纯度作为衡量数据流聚类质量的标准. 为了便于数据检测, 将数据按到达的时间点分割成4个时间段, 在实际情况中每个时刻的瞬时速度有所不同, 因此采用4个时间区间的平均速度v, 如表1所示.
| 表 1 各时间段数据流平均速度 |
通过选取中等规模的数据样本来分析数据, 设置参数如下: 微簇数量K=50; 初始化窗口大小W=500;
在图2中, 取表1不同时间区间内的数据和数据速度来对本文算法与TEDA[11]算法做聚类纯度对比. 从图2中可以看出在取聚类大小K=100时, 本文算法的聚类纯度在除第二、四个时间区间内优势不明显, 其余2个时间区间内都明显高于TEDA算法, 并且其聚类纯度都高于89%. 在这4个时间单元内, 本文算法的聚类纯度波动幅度与TEDA算法相差无几. 这是因为本文算法不仅对蜂群初始化进行了改进, 克服了其随机性; 而且在算法中加入了全局的调节因子使得使蜜蜂更快的向最优位置移动, 提高了全局搜索能力, 进而提高了聚类质量.

|
图 2 不同时间单元聚类纯度比较 |
在图3中, 取数据流速度为v=100, 数据量与时间是成正相关, 随着时间的累加, 数据量也不断增加. 聚类质量虽有下降但也有不错的聚类指标, 但是总体高于TEDA算法. 因为在处理规模较大的数据时, 初始化阈值T会有更显著的效果.

|
图 3 不同时间段聚类纯度比较 |
在经过图1、图2的实现对比后, 为了更好的显示出数据流的瞬时速度与平均速度对聚类纯度的影响, 如图4将第一时间段中前一半连续数据进行细化处理, 选取100为时间间隔点. 数据显示本文算法在各个时间单元内的聚类纯度均在98%, 整体高于TEDA算法的聚类纯度. 实验结果表明本文算法在聚类纯度、性能和效率优化等方面都有提高.

|
图 4 第一时间段内聚类纯度对比 |
为了进一步检测本文算法的延展性, 本文根据KDD-CUP-99真实数据集的连续特征属性, 合成了人工数据集. 该数据集规模分为100 K与200 K两组, 分别包含不同的维数. 由图5可以看出, 不同维度数据和算法运行时间是呈线性函数关系的, 并且在两组不同的数据规模中也均有不错的线性变化.
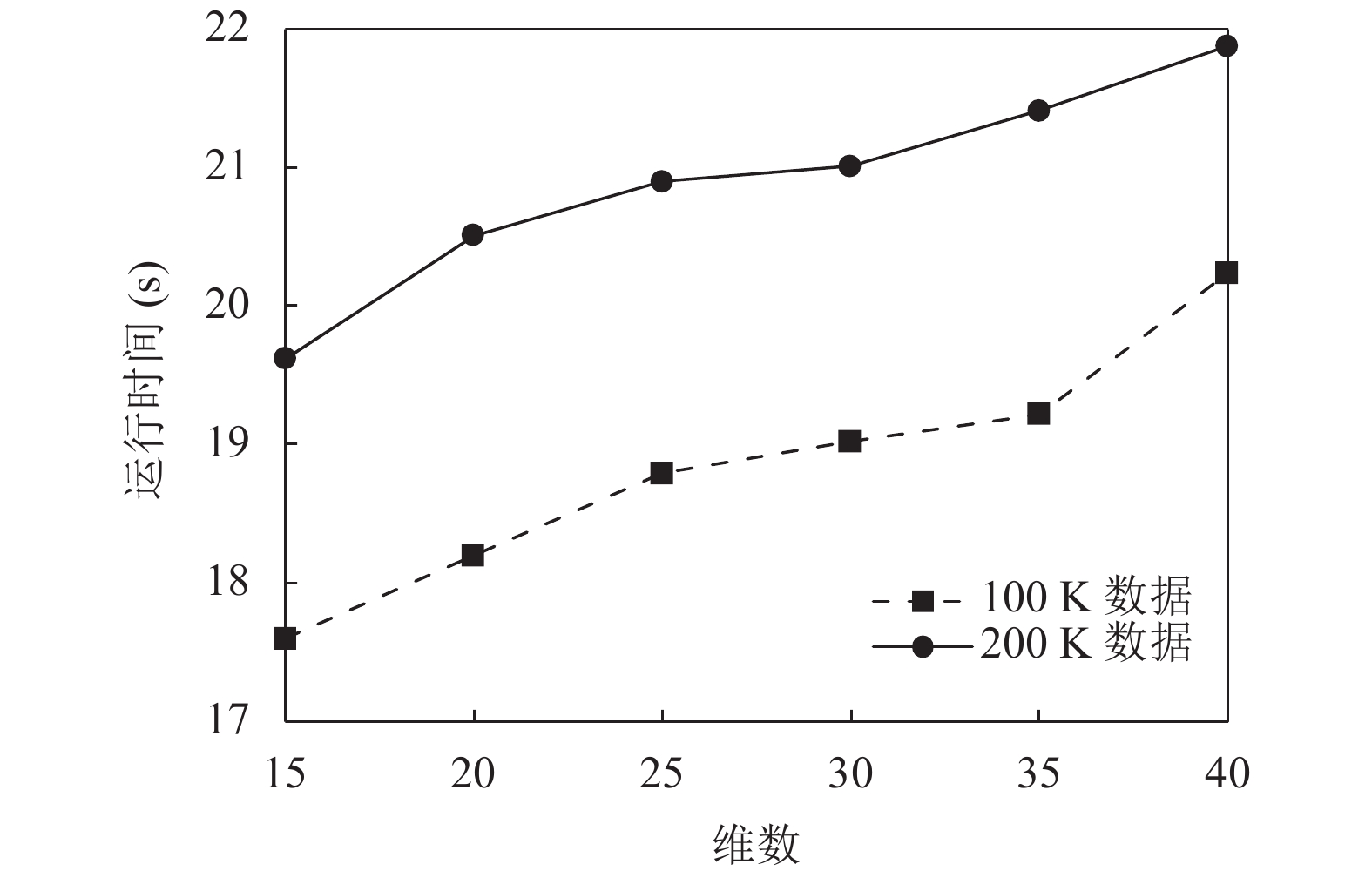
|
图 5 不同维度数据运行时间对比 |
在图6中可以看出本文算法的运行时间和簇的个数是呈线性增长的, 并且在经过多个维度的测试后表现的比较平稳, 说明簇数随着数据量的增大并没有较大的时间变化幅度. 综上所述, 本文算法在面对不同的数据以及簇数时表现出了较好的延展性和稳定性.
5 结论通过研读文献, 结合所学知识, 在动态滑动窗口模型上提出了人工蜂群优化的数据流聚类算法. 该算法通过利用动态滑动窗口、初始化阈值T以及离线部分中改进的蜂群算法, 有效的改善了聚类质量. 最后通过实验仿真的结果可以看出本文算法相比于TEDA算法提高了聚类质量, 并有较好的延展性和稳定性.

|
图 6 运行时间随簇个数的变化 |
| [1] |
Ding SF, Wu FL, Qian J, et al. Research on data stream clustering algorithms. Artificial Intelligence Review, 2015, 43(4): 593-600. DOI:10.1007/s10462-013-9398-7 |
| [2] |
Aggarwal CC, Han JW, Wang JY, et al. A framework for clustering evolving data streams. Proceedings of the 29th International Conference on Very Large Data Bases. Berlin, Germany. 2003. 81–92.
|
| [3] |
周华平, 陈顺生. 基于动态可调衰减滑动窗口的变速数据流聚类算法. 计算机应用与软件, 2015, 32(11): 255-260, 300. DOI:10.3969/j.issn.1000-386x.2015.11.059 |
| [4] |
Fahy C, Yang SX, Gongora M. Ant colony stream clustering: A fast density clustering algorithm for dynamic data streams. IEEE Transactions on Cybernetics, 2019, 49(6): 2215-2228. DOI:10.1109/TCYB.2018.2822552 |
| [5] |
肖裕权, 周肆清. 基于粒子群优化算法的数据流聚类算法. 计算机技术与发展, 2011, 21(10): 43-46, 50. DOI:10.3969/j.issn.1673-629X.2011.10.011 |
| [6] |
张忠平, 王浩, 薛伟, 等. 动态滑动窗口的数据流聚类方法. 计算机工程与应用, 2011, 47(7): 135-138. DOI:10.3778/j.issn.1002-8331.2011.07.039 |
| [7] |
Karaboga D. An idea based on honey bee swarm for numerical optimization. Kayseri, Turkey: Erciyes University, 2005.
|
| [8] |
周涓, 熊忠阳, 张玉芳, 等. 基于最大最小距离法的多中心聚类算法. 计算机应用, 2006, 26(6): 1425-1427. |
| [9] |
喻金平, 郑杰, 梅宏标. 基于改进人工蜂群算法的K均值聚类算法. 计算机应用, 2014, 34(4): 1065-1069, 1088. |
| [10] |
吴建胜, 张文鹏, 马垣. KDDCUP99数据集的数据分析研究. 计算机应用与软件, 2014, 31(11): 321-325. DOI:10.3969/j.issn.1000-386x.2014.11.081 |
| [11] |
廖江陵, 管有庆. 一种改进的模糊数据流聚类算法. 计算机技术与发展, 2017, 27(11): 96-100. DOI:10.3969/j.issn.1673-629X.2017.11.021 |
 2020, Vol. 29
2020, Vol. 29


