1 图像分割简介

图像分割和边缘检测是计算机视觉, 特别是图像分析中一个基础而重要的问题(如: 目标识别和图像解析), 其目的是把一幅给定图像根据其图像特征(如: 边缘, 颜色, 纹理, 运动, 角点特征等)划分为不同区域^[1]. 近年来, 随着计算机技术发展, 使得图像分割成文现代科学领域的研究热点, 图像分割在医学图像分析, 遥感, 监测等领域得到广泛应用^[2–11]. 在诸如物体识别, 分类和分割的应用中寻找物体边缘是非常重要的一步. 因此, 使用和设计何种边缘检测算法直接影响这些应用性能. 如: 2019年Yuan等^[12]提出了一个量子图像边缘检测算法, 将边缘检测算法灵活应用于量子计算. 图像边缘检测在雷达图像检测中也有重要应用, Ma等^[13]提出通过稀疏表示进行SAR图像边缘检测, 作者提出了一种基于去噪算法的新型合成孔径雷达(SAR)图像检测算法, 该算法通过稀疏表达和一种新的形态学边缘检测器. 首先, 作者将Shearlet变换应用于SAR图像以获得图像的稀疏表示. 然后, 将带方向的形态学边缘检测器应用于Shearlet的方向子带系数, 其通过迭代去噪处理来恢复. 2019年Sert等^[14]提出了一个新的基于最大范数熵的中智学边缘检测方法. 同时, 边缘检测算法在医学图像领域也有重要应用, 随着医学领域成像技术的快速发展, 不同模态的医学图像具有不同的成像原理, 反映了人体生理信息的不同重点和缺陷. 边缘检测是医学超声图像处理的关键步骤, 检测结果将直接影响医生对疾病的诊断. 图像边缘检测可以看作边缘点和非边缘点的分类问题. 基于此, Song等于2019年^[15]提出了基于改进差分进化算法和Prewitt算子的医学图像边缘检测. Churchill等于2019年^[16]提供了理论证据来解释边缘位置在CT影像重建中的潜在重要性. 然后开发一种实用的方案来利用这一理论. 最后, 作者通过实验证实了提出的使用边缘遮蔽正则化可以提高CT重建的准确性和重建速度.

近年来, 基于变分法和偏微分方程(PDES)的图像分割方法得到了广泛研究^[17–24]. 早期图像分割模型代表为活动轮廓模型, 活动轮廓模型根据图像边缘信息和区域信息对给定图像进行分割. 基于边缘信息和区域信息考虑, Kass等于1988年提出基于边缘信息的能量最小化方法, 即, Snake模型^[25]. 其后, 受到Snake活动轮廓模型启发, Caselles等提出了综合活动轮廓长度信息, 提出了几何活动轮廓模型^[26], 与此同时, Mumford和Shah提出了基于区域信息图像分割变分框架, 即, 著名的Munmford-Shah (MS)模型^[27]. 但是, 由于MS模型能量泛函的非凸性, 导致在当时对该模型直接求解十分困难. 所以, Chan和Vese为了克服MS模型所存在的弊端, 并整合了变分法和水平集方法^[17], 提出了Chan-Vese (CV)模型^[28].

由于CV模型应用广泛, 所以在过去几十年里, 该模型一直受到研究学者青睐. 同时, 各研究学者开发各种对该模型求解的有效方法, 例如: 为克服初始化轮廓敏感度问题, Li等^[29]修改CV模型, 提出了利用惩罚函数作为约束且无需初始化过程的图像分割模型. 2014年Duan等^[30]综合了变量分离法, 对偶方法, Bregman迭代和增广的拉格朗日方法提出了更快更有效更的算法. 这些算法在高计算精度和无需初始化方面取得重要成果.

随着计算机技术的发展, 深度学习在图像分割中取得重要进展, 最显著的进展是深度卷积神经网络(CNNS)不断被应用到场景解析中. 典型的网络包括: DeepLab (V1-V3)^[31,32], Refinenet^[33], PSP-Net^[34]和DANet^[35], 然而, 这些模型的缺点是计算代价相当大, 需要学习的参数特别多, 为了降低这些模型在场景解析中的计算复杂度, 过去几年里, 很多学者在降低计算复杂度方面做了大量工作. 例如: ENet^[36], ESPNet^[37]大量减少了需要学习的参数.

但是, 上述所提的变分优化模型中, 基本上都是假设图像所含噪声为高斯噪声, 几乎是用L2范数对高斯噪声加以拟合. 然而在现实生活中, 情况相对较为复杂, 往往图像在成像时还有来自外加噪声的污染, 幸运的是, 外加噪声可以用L1范数得以很好拟合^[38,39]. 利用L1范数作为数据拟合项作为分段常数图像分割模型, 并利用二阶正则函数(TV2)对目标函数加以惩罚, 使得所提出模型能更好地逼近目标函数的同时还能能更好地分割低对比度和含有外加噪声的图像. 再者, 本文通过变量分离方法把一复杂非凸问题转换为若干个简单凸子问题进行求解, 从而巧妙地处理了不可导项和正则项.

2 预备知识

在本节中, 因为Alternating Direction Method of Multipliers (ADMM)或Split Brgman迭代^[40]方法是求解线性约束凸二次规划问题的有效方法, 所以在此对该方法做如下简单介绍. 考虑如下线性约束凸优化问题:

$\left\{ {\begin{array}{*{20}{c}} {\mathop {\min }\limits_{u \in {R^N}} {E_1}\left( u \right) + {E_2}\left( v \right)} \\ {{A_1}u + {A_1}v = f} \end{array}} \right. $

(1)

其中, 通过上述目标函数, 可得如下增广拉格朗日泛函:

$\left\{ {\begin{aligned} & \left( {{u^{k + 1}}, {v^{k + 1}}} \right) \in \mathop {\min }\limits_{u, v} {E_1}\left( u \right) + {E_2}\left( v \right) + \frac{\gamma }{2}\left\| {{A_1}u + {A_1}v - f - {b^k}} \right\|_2^2 \\ & {{b^{k + 1}} = {b^k} - \left( {{A_1}{u^{k + 1}} + {A_1}{v^{k + 1}} - f - {b^k}} \right)} \end{aligned}} \right. $

(2)

当上述系统方程满足某些收敛条件时, ADMM方法在(2)中固定 $v$ 更新 $u$ , 固定 $u$ 更新 $v$ . 因此, ADMM算法可以总结如算法1.

算法1. ADMM算法

初始化: 设k=0, 选择 $\scriptstyle \gamma > 0$ , $ \scriptstyle{u^0}$ , $\scriptstyle{v^0}$ and $\scriptstyle{b^0} = 0$ ;

for $\scriptstyle k = 1, 2, 3, \cdots , K$ do

(1)解问题

$\scriptstyle \mathop {\arg \min }\limits_u {E_1}\left( u \right) + \frac{\gamma }{2}\left\| {{A_1}u + {A_2}v - f - {b^k}} \right\|_2^2$ ;

(2)求解问题

$\scriptstyle\mathop {\arg \min }\limits_u {E_2}\left( v \right) + \frac{\gamma }{2}\left\| {{A_1}u + {A_2}v - f - {b^k}} \right\|_2^2$ ;

(3)拉格朗日乘子更新

$\scriptstyle{b^{k + 1}} = {b^k} - \left( {{A_1}{u^{k + 1}} + {A_2}{v^{k + 1}} - f} \right)$ ;

end

对上述最小值问题直接求解 $\left( {{u^{k + 1}}, {v^{k + 1}}} \right)$ 十分困难, 因为从式(2)拉格朗日泛函中可知, 该数学表达式中涉及一项不可分离的二次项, 该二次项也可能是非光滑项. 所以对于该目标函数, 一个很自然的方法是应用非线性block-Guass-Seidel技术(NLBGS)对 $u$ 和 $v$ 固定其中一个变量, 从而对另外一个变量轮换求解, 经过这样的处理, 与NLBGS方法相比ADMM计算代价更小, 更加容易求解, 故该方法在近几年得到十分广泛地使用与研究.

3 模型提出与数值求解

在本节中将介绍所提出的高阶正则图像轮廓检测算法, 随后用变量分离法和ADMM算法对该模型详细优化过程和部分收敛性分析加以描述.

设 $f: {\left[ {0, 1} \right]^2} \to R \subset {L^1}\left( \Omega \right)$ 为观测到信号(图像), 且满足如下数学表达式, $f = u + n$ , 其中 $u$ 为未受噪声污染信号(图像), $n$ 为外加噪声(IN). 为了重建 $u$ , 可以考虑如下优化问题:

$\mathop {\min }\limits_u \left\{ {\lambda {{\left\| {f - u} \right\|}_1} + {{\left\| {\nabla u} \right\|}_1}} \right\}$

(3)

其中, $\nabla u$ 为 $u$ 的分布导数, ${\left\| {\nabla u} \right\|_1}$ 为著名的total variation (TV)^[41]有界变差空间中的半范数, $\lambda > 0$ 为权参数. 若用L2-数据拟合项 ${\left\| {f - u} \right\|_2}$ 替代 ${\left\| {f - u} \right\|_1}$ 数据拟合项, 从而可得经典的Rudin-Osher-Fatemi (ROF)^[41]模型. 从而图像分割模型数学表达式如下:

$\mathop {\min }\limits_u \left\{ {\lambda {{\left\| {f - u} \right\|}_1} + {H^1}\left( \Gamma \right)} \right\}$

(4)

其中, $\Gamma $ 为 $u$ 的不连续集合, ${H^1}$ 为一维的Hausdorff测度, 即, $\Gamma $ 的长度.

假设区域 ${\left[ {0, 1} \right]^2}$ 被划分为如下的 $N$ 个区域, ${\Omega _1}, $ $ {\Omega _2}, \cdots , {\Omega _N}$ 且同时满足 ${ \cup _{i = 1,\cdots , N}}{\Omega _i} = {\left[ {0, 1} \right]^2}$ , $ {\Omega _i} \cap {\Omega _j} = \phi $ , $i \ne j$ , 且 $u =\displaystyle \sum\limits_{i = 1}^N {{c_i}{\chi _{{\Omega _i}}}} $ 对于所有的 $i$ 具有 ${c_i} \in R$ . 特别地, 当 $N = 2$ 可以得到除了数据拟合项之外, 其他都类似于CV模型的模型.

$\mathop {\min }\limits_{{c_1}, {c_2}} \left\{ {\lambda \int\limits_\Omega {\left| {f - {c_1}} \right|dx + \lambda \int\limits_{{\Omega ^c}} {\left| {f - {c_1}} \right|dx + \lambda \int\limits_{\partial \Omega } {ds} } } } \right\}$

(5)

由于 ${\left\| {f - u} \right\|_1}$ 不可微, 所以可以通过迭代得出 ${c_1}$ , ${c_2}$ 近似解. 在图像恢复中, 尽管基于TV^[41]正则已经取得了很好的效果, 但是在图像恢复过程中TV正则会引起阶梯效应. 而高阶正则不仅有可以去除阶梯效应的功能, 而且高阶正则还有光滑区域, 很好地保持物体边缘的效果, 在本模型的实验过程中, 假设图像都是带有噪声的, 又因为高阶正则比低阶正则更具有光滑性和非线性性, 所以为了更高的提取边缘信息, 综合Jung等^[38]提出的模型, 我们提出如下的高阶正则图像边缘检测模型:

$\mathop {\min }\limits_{{c_1}, {c_2}, u} {\left\{ {\lambda {{\left\| {f - {c_1}} \right\|}_1}u + \lambda {{\left\| {f - {c_2}} \right\|}_1}\left( {1 - u} \right)} \right. } {\left. { + \alpha {{\left\| {\nabla u} \right\|}_1} + \beta {{\left\| {\Delta u} \right\|}_1}} \right\}} $

(6)

其中, $\nabla u = \left( {{D_x}u, {D_y}u} \right), \;\Delta u = \left( {{D_{xx}}u, {D_{yy}}u, {D_{xy}}u, {D_{yx}}u} \right) $ 分别是离散的一阶偏导数算子和二阶偏导数算子(拉普拉斯算子), 所有离散的一阶偏导数算子和二阶偏导数算子 ${D_x}, {D_y}, {D_{xx}}, {D_{yy}}, {D_{xy}}$ 都来自于 ${R^{M \times N}} \to {R^{M \times N}}$ . 我们可以证明上述目标函数的解存性, 这不是本文的讨论重点, 故此省略.

通过观察上述目标函数可以发现, 为了对该目标泛函进行求解, $\left( {{c_1}, {c_2}, u} \right)$ , 即, 两步骤算法: 第1步: 先固定 $u$ 求解 ${c_1}, {c_2}$ , 第2步: 固定 ${c_1}, {c_2}$ 求解 $u$ . 同时并对离散的散度算子做了如下定义, 且散度算子 $div: $ ${\left( {{R^{M \times N}}} \right)^2} \to {R^{M \times N}}$ 具有如下的共轭性质. $- div. u = p. \nabla u, $ $ \forall u \in {R^{N \times M}}, p \in {\left( {{R^{M \times N}}} \right)^2}$ .

故此, 离散散度算子可以作如下定义: 对

$\begin{array}{*{20}{c}} {p = \left( {{p_1}, {p_1}} \right) \in {{\left( {{R^{M \times N}}} \right)}^2}} \\ {divp\left( {i, j} \right) = {D_x}{p_1}\left( {i, j} \right) + {D_y}{p_2}\left( {i, j} \right)} \end{array}$

其中, ${D_x}$ 和 ${D_y}$ 为如下的向前向后分算子.

以此类推, 离散二阶散度算子定义如下: $ di{v^2}:$ $ {\left( {{R^{N \times M}}} \right)^4} \to {R^{N \times M}}$ . 且具有如下共轭性质: $di{v^2}q. u = $ $q. \Delta u , \forall u \in {R^{M \times N}}, q \in {\left( {{R^{N \times M}}} \right)^4} $ . 对于, $ q = ( {q_{11}},{q_{12}}, {q_{21}}, {q_{22}} ) \in$ $ {\left( {{R^{N \times M}}} \right)^4}$ , 我们定义, $di{v^2}q\left( {i, j} \right)\! = \! {D_{xx}}{q_{11}}\left( {i, j} \right) \!+\! {D_{xy}}{q_{12}}\left( {i, j} \right) \! + $ ${D_{yy}}{q_{21}}\left( {i, j} \right) + {D_{yx}}{q_{22}}\left( {i, j} \right) $ .

在实际应用中, 学者经常用算子分离法(split Bregman iteration和ADMM)对(6)进行求解. 为达到求解目的, 本文先把(6)无约束优化问题转化成一个有约束优化问题, 从而利用Bregman iteration进行求解, 引入中间变量的好处在于: 通过引入如下辅助变量, 不仅把无约束优化问题变成一个有约束优化问题, 引入辅助变量使用变量分离法把一个复杂问题分解成若干简单子问题, 使得分别对各子问题求解相对容易.

$\left\{ {\begin{array}{*{20}{c}} {\mathop {\min }\limits_{{c_1}, {c_2}, u, v, w} \left\{ {\begin{array}{*{20}{c}} {\lambda {{\left\| {f - {c_1}} \right\|}_1}u + \lambda {{\left\| {f - {c_2}} \right\|}_1}\left( {1 - u} \right)} \\ { + \alpha {{\left\| {\nabla u} \right\|}_1} + \beta {{\left\| {\Delta u} \right\|}_1}} \end{array}} \right\}} \\ {v = \nabla u, w = \Delta u} \end{array}} \right. $

(7)

其中, $v = \left( {{v_x}, {v_y}} \right)$ , $w = \left( {{w_{xx}}, {w_{yy}}, {w_{xy}}, {w_{yx}}} \right)$ . 这里需要进行说明的是该符号不是对 $v, w$ 分别求导, 而是表示坐标. 显而易见, 无约束优化问题(6)和有约束优化问题(7)等价, 从而可以利用ADMM或Split Bregman迭代进行求解. 其中, 问题(7)等价于:

$ \mathop {\min }\limits_{{c_1}, {c_2}, u, v, w} \left\{ {\begin{array}{*{20}{c}} {\lambda {{\left\| {f - {c_1}} \right\|}_1}u + \lambda {{\left\| {f - {c_2}} \right\|}_1}\left( {1 - u} \right)} \\ { + \alpha {{\left\| v \right\|}_1} + \beta {{\left\| w \right\|}_1}} \\ { + \dfrac{{{\gamma _1}}}{2}\left\| {v - \nabla u + b_1^k} \right\|_2^2 + \dfrac{{{\gamma _2}}}{2}\left\| {w - \Delta u + b_2^k} \right\|_2^2} \end{array}} \right\} $

(8)

Bregmen迭代算法总结如算法2.

算法2. Bregman迭代图像边缘检测算法

初始化: 设k=0, 选择 $\scriptstyle{u^1} = {u_0}, {v^1} = \nabla {u_0}, {w^1} = \Delta {u_0}$ and $\scriptstyle b_1^k = 0, b_2^k = 0$ ;

for $\scriptstyle k = 1, 2, 3, \cdots , K$ do

　　计算(8)的最优解;

　　更新: $\scriptstyle b_1^{k + 1} = b_1^k + {v^{k + 1}} - \nabla {u^{k + 1}}$ ;

　　更新: $\scriptstyle b_2^{k + 1} = b_2^k + {w^{k + 1}} - \Delta {u^{k + 1}}$ ;

end

直接对(8)求解时十分困难, 从而可把上式分离成多个单变量, 即, 把一个复杂问题分解成几个子问题求解. Split Bregman iteration第一次被Goldstain和OSher^[40]提出, 它在很多宽松条件下等价于ADMM算法. 该方法被广泛地应用到图像噪声去除, 图像去模糊, 图像修补等相关领域.

3.1 u-子问题

对 $u$ -子问题进行求解时首先固定 $r = \left| {f - {c_1}} \right| + $ $\left| {f - {c_2}} \right|$ . 得到如下目标泛函:

$\mathop {\min }\limits_u \left\{ {\lambda \int {rudx + } \dfrac{{{\gamma _1}}}{2}\left\| {v\! - \!\nabla u \!+\! b_1^k} \right\|_2^2} {\! + \!\dfrac{{{\gamma _2}}}{2}\left\| {w \!-\! \Delta u \!+\! b_2^k} \right\|_2^2} \right\}$

(9)

此优化问题可以通过其优化条件加以求解, 在连续情况下, 其解为四阶线性PDE, 离散情况, 其优化条件如下:

$ \left( {{\gamma _1}\Delta + {\gamma _2}{\Delta ^2}} \right)u = \lambda r + {\gamma _1}div\left( {v + b_1^k} \right) + {\gamma _2}div\left( {w + b_2^k} \right) $

(10)

通过FFT (快速傅里叶变换)可以得到(10)如下近似解. 其中, ${\cal F}$ 代表傅里叶变换, ${{\cal F}^{ - 1}}$ 代表傅里叶的逆变换.

${u^{k + 1}} = {{\cal F}^{ - 1}}\left( {{\cal F}\left( {\frac{{ {\lambda r + {\gamma _1}div\left( {v + b_1^k} \right)} { + {\gamma _2}div\left( {w + b_2^k} \right)} }}{{{\gamma _1}\Delta + {\gamma _2}{\Delta ^2}}}} \right)} \right)$

(11)

3.2 v-子问题

$v$ -子问题等价于求解如下优化问题:

${v^{k + 1}} = \mathop {\min }\limits_v \alpha {\left\| v \right\|_1} + + \frac{{{\gamma _1}}}{2}\left\| {v - \nabla u + b_1^k} \right\|_2^2$

(12)

上述优化问题的解可以使用收缩算子^[42]表达, 其解析表达如下:

${v^{k + 1}} = shrink\left( {\nabla {u^{k + 1}} - b_1^k, \frac{\alpha }{{{\gamma _1}}}} \right)$

(13)

其中, 收缩算子shrink (x)^[42]定义如下:

对于任意点 $\alpha \in {\left[ {0, 1} \right]^2}$ , 为了方便起见, 令 $0. \left( {\dfrac{0}{0}} \right){\rm{ = }}0$ .

$shrink\left( {{s_\alpha }, {t_\alpha }} \right) = \frac{{{s_\alpha }}}{{\left| {{s_\alpha }} \right|}}\max \left( {{s_\alpha } - {t_\alpha }, 0} \right)$

(14)

3.3 w-子问题

$w$ -子问题满足如下优化条件:

${w^{k + 1}} = \mathop {\min }\limits_w \beta {\left\| w \right\|_1} + \frac{{{\gamma _2}}}{2}\left\| {w - \Delta u + b_2^k} \right\|_2^2$

(15)

类似于 $v$ -子问题, 上述优化问题解为具有收缩性质的软阈算子.

${w^{k + 1}} = shrink\left( {\Delta {u^{k + 1}} - b_2^k, \frac{\beta }{{{\gamma _2}}}} \right)$

(16)

为了说明收缩算子的表达效果和设置依据我们考虑如下的一维最小值问题加以说明:

$\mathop {\min }\limits_x \left\{ {\frac{1}{{2\alpha }}{{\left( {x - h} \right)}^2} + \lambda \left| x \right|} \right\}$

(17)

其中, $x, h$ 都为标量. 令 $Q\left( x \right) = \dfrac{1}{{2\alpha }}{\left( {x - h} \right)^2} + \lambda \left| x \right|$ , 可得:

$Q\left( x \right) = \left\{ {\begin{aligned} & {\frac{1}{{2\alpha }}\left( {x - 2hx + 2\lambda \alpha x + {h^2}} \right),{\text{若}}x > 0}\\ & {\frac{1}{{2\alpha }}\left( {x - 2hx - 2\lambda \alpha x + {h^2}} \right),{\text{若}}x < 0} \end{aligned}} \right.$

(18)

当 $h \ge \lambda \alpha $ 时, $Q\left( x \right)$ 的最小值为 $h - \lambda \alpha \ge 0$ ; 当 $h \le - \lambda \alpha $ 时, $Q\left( x \right)$ 的最小值为 $h + \lambda \alpha \le 0$ ; 当 $ - \lambda \alpha < h < \lambda \alpha $ 时, $Q\left( x \right)$ 的最小值为0. 所以, 最小值问题(17)可以用如下收缩算子更新:

${x^{k + 1}} = \left\{ {\begin{aligned} & {{h^k} - \lambda \alpha ,{\text{若}}{h^k} \ge \lambda \alpha } \\ & {0,{\text{若}} - \lambda \alpha < {h^k} < \lambda \alpha }\\ & {{h^k} - \lambda \alpha ,{\text{若}}{h^k} \le - \lambda \alpha } \end{aligned}} \right.$

(19)

收缩算子对稀疏解是有利的, 最终大量的 $h$ 值会趋近于区间 $\left[ {{\rm{ - }}\lambda \alpha {\rm{, }}\lambda \alpha } \right]$ 的某个值从而使得 $x$ 变得稀疏. 当 $\lambda $ 值越大, 区间 $\left[ {{\rm{ - }}\lambda \alpha {\rm{, }}\lambda \alpha } \right]$ 就越大, 从而使得 $x$ 的解就越稀疏.

对于本模型来说若图像的大小为 $N \times N$ , 以式(13) 为例, 其线性时间复杂度为 ${\rm O}\left( {{N^2}} \right)$ , 所以, $v, w$ -子问题可以被快速求解, 综上所述, 对于 $v, w$ -子问题我们设置了如式(14)的收缩算子是合理的.

3.4 ${c_1},{c_2}$ -子问题

现考虑如下最小值问题, 从而得到 ${c_1}, {c_2}$ 的近似解. 先固定 $u$ , 得到如下最小值问题:

${c_i} \in \mathop {\arg \min }\limits_{{c_i}} \left\{ {\lambda \int {\left| {f - {c_i}} \right|h\left( x \right){\rm d}x} } \right\}$

(20)

其中, 当 $i = 1$ 时, $h = u$ , 当 $i = 2$ 时, $h = 1 - u$ .

首先我们定义区域 ${\left[ {0, 1} \right]^2}$ 上的特征函数, $ \chi =$ $ \left\{ {\begin{array}{*{20}{c}} {1, x \in {{\left[ {0, 1} \right]}^2}} \\ {0, x \notin {{\left[ {0, 1} \right]}^2}} \end{array}} \right. $ , 从而常数值 ${c_i}$ 可以用如下的表达式来代替 $\chi {c_i}$ , 从而可以重写最小值(20):

${c_i} \in \mathop {\arg \min }\limits_{{c_i}} {\left| {f - {c_i}} \right|_h}$

(21)

其中,

$ {\left| {f - {c_i}} \right|_h} = \int {\left| {f - {c_i}} \right|h\left( x \right){\rm d}x} $

(22)

为使用变量分离法, 故此引入如下辅助变量,

$\left\{ {\begin{array}{*{20}{c}} {\mathop {\min }\limits_{{c_i}, {e_i}} \left\{ {\lambda {{\left| {{e_i}} \right|}_u}} \right\}} \\ {{e_i} = f - \chi {c_i}} \end{array}} \right. $

(23)

式(23)可以通过ADMM或Split Bregman迭代进行求解.

$\mathop {\arg \min }\limits_{{c_i}} \left\{ {\frac{{{\eta _i}}}{2}\int {{{\left( {\chi {c_i} + {e_i} - f - d_i^k} \right)}^2}{\rm d}x} } \right\}$

(24)

$\mathop {\arg \min }\limits_{{e_i}} \left\{ { {\lambda {{\left| {{e_i}} \right|}_h}} { + \frac{{{\eta _i}}}{2}\int {{{\left( {\chi c_i^{k + 1} + {e_i} - f - d_i^k} \right)}^2}{\rm d}x} } } \right\}$

(25)

$d_i^{k + 1} = d_i^k - \left( {\chi c_i^{k + 1} + e_i^{k + 1} - f} \right)$

(26)

从而, $c_i^{k + 1}$ 和 $e_i^{k + 1}$ 的近似解解析表达式为:

$c_i^{k + 1} = \frac{{\int {d_i^k - e_i^k + f{\rm d}x} }}{{\int {{\rm d}x} }}$

(27)

$ e_i^{k + 1} = shrink\left( {f + d_i^k - \chi c_i^{k + 1}, \frac{{\lambda u}}{{{\eta _i}}}} \right) $

(28)

故此ADMM图像边缘检测算法总结如算法3.

算法3. ADMM图像边缘检测算法

初始化: 设k=0, 选择 $\scriptstyle \lambda $ , $\scriptstyle {\eta _1}$ , $\scriptstyle {\eta _2}$ , $\scriptstyle \alpha $ , $\scriptstyle \;\beta > 0$ , $\scriptstyle {\gamma _1}, {\gamma _2} >0, \;b_1^k ={v^0} =0, $ $\scriptstyle b_2^k = {w^0} = 0, e_i^0 = d_i^0 = 0$ $\scriptstyle {u^0} = 1$ 在某些区域 $\scriptstyle \Omega \subset {\left[ {0, 1} \right]^2}$ , 0其他;

for $\scriptstyle k = 1, 2, 3, \cdots , K$ do

　　　 $\scriptstyle {h^k} = {u^k}$ if $\scriptstyle i = 1$ , $\scriptstyle {h^k} = \left( {1 - {u^k}} \right), i = 2$ ,

　　　计算 $\scriptstyle c_i^{k + 1}$ : 用式(27)计算 $\scriptstyle c_i^{k + 1}$ , $\scriptstyle i = 1, 2$ ;

　　　计算 $\scriptstyle e_i^{k + 1}$ : 用式(28)计算 $\scriptstyle e_i^{k + 1}$ , $\scriptstyle i = 1, 2$ ;

　　　更新 $\scriptstyle d_i^{k + 1}$ : 用式(26)计算 $\scriptstyle d_i^{k + 1}$ , $\scriptstyle i = 1, 2$ ;

　　　计算 $\scriptstyle {r^{k + 1}}$ : 用 $\scriptstyle {r^{k + 1}} = \left| {f - c_1^{k + 1}} \right| - \left| {f - c_2^{k + 1}} \right|$ ;

　　　计算 $\scriptstyle {v^{k + 1}}$ : 用式(13)计算 $\scriptstyle {v^{k + 1}}$ ;

　　　计算 $\scriptstyle {w^{k + 1}}$ : 用式(16)计算 $\scriptstyle {w^{k + 1}}$ ;

　　　计算 $\scriptstyle {u^{k + 1}}$ : 用式(11)计算 $\scriptstyle {u^{k + 1}}$ ;

　　　更新 $\scriptstyle b_1^{k + 1}$ : $\scriptstyle b_1^{k + 1} = b_1^k + {v^{k + 1}} - \nabla {u^{k + 1}}$ ;

　　　更新 $\scriptstyle b_2^{k + 1}$ : $\scriptstyle b_2^{k + 1} = b_2^k + {w^{k + 1}} - \Delta {u^{k + 1}}$ ;

end

4 算法部分收敛性分析

本节中, 受到文献[38]启发, 本文将给出本算法的部分收敛性分析, 最小值问题(6)可以通过引入变量分离办法重写成有约束条件:

$ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_{{c_1}, {c_2}, u, {e_1}, {e_2}, v, w} \lambda \int {\left| {{e_1}} \right|} udx \!+ \! \lambda \int {\left| {{e_2}} \right|} \left( {1 \! - \! u} \right)dx \!+ \! \alpha {{\left\| v \right\|}_1} \!+ \beta {{\left\| w \right\|}_1}} \\ {{e_i} = f - \chi {c_i}, v = \nabla u, w = \Delta u, i = 1, 2} \end{array}} \right. $

(29)

其对应的拉格朗日泛函如下:

$ \begin{array}{l} L\left( {{c_1}, {c_2}, u, {e_1}, {e_2}, v, w, {\mu _1}, {\mu _2}, {\mu _3}, {\mu _4}} \right) \\ = \lambda \displaystyle\int {\left| {{e_1}} \right|} udx + \lambda \displaystyle\int {\left| {{e_2}} \right|} \left( {1 - u} \right)dx + \alpha {\left\| v \right\|_1} + \beta {\left\| w \right\|_1} \\ - \displaystyle\int {{\mu _1}} \left( {v - \nabla u} \right)dx - \int {{\mu _2}} \left( {{e_1} + \chi {c_1} - f} \right)dx \\ - \displaystyle\int {{\mu _3}} \left( {{e_2} + \chi {c_2} - f} \right)dx - \int {{\mu _4}} \left( {w - \Delta u} \right)dx \\ + {\gamma _1}\left\| {v - \nabla u} \right\|_2^2 + {\gamma _2}\left\| {w - \Delta u} \right\|_2^2 \\ + {\gamma _3}\left\| {{e_1} + \chi {c_1} - f} \right\|_2^2 + {\gamma _4}\left\| {{e_2} + \chi {c_2} - f} \right\|_2^2 \end{array} $

(30)

其中, ${\mu _1}, {\mu _2}, {\mu _3}$ 为对偶变量.

设 ${X^*} = \left( {c_1^*, c_2^*, {u^*}, e_1^*, e_2^*, {v^*}, {w^*}, \mu _1^*, \mu _2^*, \mu _3^*, \mu _4^*} \right)$ 为问题(29)的KKT点, 则点 ${X^*}$ 满足如下的KKT条件:

$\left\{ {\begin{array}{*{20}{l}} {\int {\mu _2^*dx = 0} } \\ {\int {\mu _3^*dx = 0} } \\ {\lambda \left| {e_1^*} \right| - \lambda \left| {e_2^*} \right| - div\mu _1^* = 0} \\ {0 \in \lambda \partial \left| {e_1^*} \right| \odot {u^*} - \mu _2^*} \\ {0 \in \lambda \partial \left| {e_2^*} \right| \odot \left( {1 - {u^*}} \right) - \mu _3^*} \\ {0 \in \partial \left| {{v^*}} \right| - \mu _1^*} \\ {0 \in \partial \left| {{w^*}} \right| - \mu _4^*} \\ {{v^*} = \nabla {u^*}, {w^*} = \Delta {u^*}} \\ {e_i^* = f - \chi c_i^*, i = 1, 2} \end{array}} \right. $

(31)

其中, $x \odot y$ 为coordinate-wise乘法.

定理. 设 ${X^k} = \left( {c_1^k,c_2^k,{u^k},e_1^k,e_2^k,{v^k},{w^k},d_1^k,d_2^k,b_1^k,b_2^k} \right)$ 为算法3中的迭代, 并且, 设:

${\tilde X^k} = \left( c_1^k, c_2^k, {u^k}, e_1^k, e_2^k, {v^k}, {w^k}, {\gamma _1}d_1^k, {\gamma _2}d_2^k, {\gamma _3}b_1^k, {\gamma _4}b_2^k \right)$

假设,

$\mathop {\lim }\limits_{k \to \infty } \left( {{X^k} - {X^{k - 1}}} \right) = 0.$

则任意 ${\tilde X^k}$ 的点集是问题(29)的KKT条件.

证明: 首先, 对于 $u$ -子问题等价于求解最小化问题(9), 从而得出如下优化条件:

$ \left( {{\gamma _1}\Delta \! +\! {\gamma _2}{\Delta ^2}} \right){u^{k + 1}} \! =\! \lambda r \!+\! {\gamma _1}div\left( {{v^k}\! +\! b_1^k} \right) \!+ \!{\gamma _2}div\left( {{w^k}\! +\! b_2^k} \right) \!\!\! $

(32)

其中, $r = \left| {f - c_1^{k + 1}} \right| - \left| {f - c_2^{k + 1}} \right|.$

其次, 从优化条件和ADMM算法对各变量的表达式可得:

$ \int {dx\left( {c_i^{k + 1} - c_i^k} \right)} = \int - e_i^k + f + d_i^k - \chi c_i^k{\rm d}x, i = 1, 2 $

(33)

$\begin{aligned}[b] & \left( {{\gamma _1}\Delta + {\gamma _2}{\Delta ^2}} \right)\left( {{u^{k + 1}} - {u^k}} \right) = \lambda r + {\gamma _1}div\left( {{v^k} + b_1^k} \right) +\\ & {\gamma _2}div\left( {{w^k} + b_2^k} \right) - \left( {{\gamma _1}\Delta + {\gamma _2}{\Delta ^2}} \right){u^k} \end{aligned} $

(34)

$ e_1^{k + 1} - e_1^k = shrink\left( {f + d_1^k - \chi c_1^{k + 1}, \frac{{\lambda u}}{{{\gamma _3}}}} \right) - e_1^k $

(35)

$ e_2^{k + 1} - e_2^k = shrink\left( {f + d_2^k - \chi c_2^{k + 1}, \frac{{\lambda \left( {1 - u} \right)}}{{{\gamma _4}}}} \right) - e_2^k $

(36)

${v^{k + 1}} - {v^k} = shrink\left( {\nabla {u^{k + 1}} - b_1^k, \frac{\alpha }{{{\gamma _1}}}} \right) - {v^k}$

(37)

${w^{k + 1}} - {w^k} = shrink\left( {\Delta {u^{k + 1}} - b_2^k, \frac{\beta }{{{\gamma _2}}}} \right) - {w^k}$

(38)

因为, $\mathop {\lim }\limits_{k \to \infty } \left( {{X^k} - {X^{k - 1}}} \right) = 0$ , 所以当 $k \to \infty $ 时, 式(33)–式(38)的右边全部趋近于0. 由此可得,

$e_1^* = shrink\left( {e_1^* + \frac{{\mu _2^*}}{{{\gamma _3}}}, \frac{{\lambda {u^*}}}{{{\gamma _3}}}} \right)$

(39)

$e_2^* = shrink\left( {e_2^* + \frac{{\mu _3^*}}{{{\gamma _4}}}, \frac{{\lambda \left( {1 - {u^*}} \right)}}{{{\gamma _4}}}} \right)$

(40)

${v^*} = shrink\left( {{v^*} + \frac{{\mu _1^*}}{{{\gamma _1}}}, \frac{\alpha }{{{\gamma _1}}}} \right)$

(41)

${w^*} = shrink\left( {{w^*} + \frac{{\mu _4^*}}{{{\gamma _2}}}, \frac{\beta }{{{\gamma _2}}}} \right)$

(42)

所以, 根据式(33)–式(38)可得, 任意 ${\tilde X^k}$ 的点集满足KKT条件(31).

5 实验结果

为了说明本文提出算法优越性, 本文将给出该模型在灰度图像, 真实图像, 含噪声图像, CT图像的分割实验结果, 在讨论结果之前, 本文先作以下说明, 该算法的迭代终止条件应满足如下的相对容忍度, 即满足下列条件:

$\frac{{{{\left\| {{u^{k + 1}} - {u^k}} \right\|}_2}}}{{{{\left\| {{u^{k + 1}}} \right\|}_2}}} < tol$

此后, 用该模型和Chan-Vese (CV)做比较. 该算法与CV模型不同之处在于计算常数值 ${c_i}, i = 1, 2$ , 对于CV模型而言, ${c_i}, i = 1, 2$ 在每次迭代过程中都有具体迭代表达式. 该模型另外一个优点是很少依赖于初始化位置和微调参数, 在本算法中, ${\eta _1}$ , ${\eta _2}$ , $\alpha $ , $\beta > 0$ , ${\gamma _1}$ , ${\gamma _2} > 0$ , 所有参数都相对很固定. 因为该模型是一个局部极小值问题, 不同初始轮廓可能会收敛到不到能量局部极小值. 我们之所以选择和CV模型作比较, 主要原因在于想体现高阶正则模型与低阶正则模型对图像边缘检测不同效果影响.

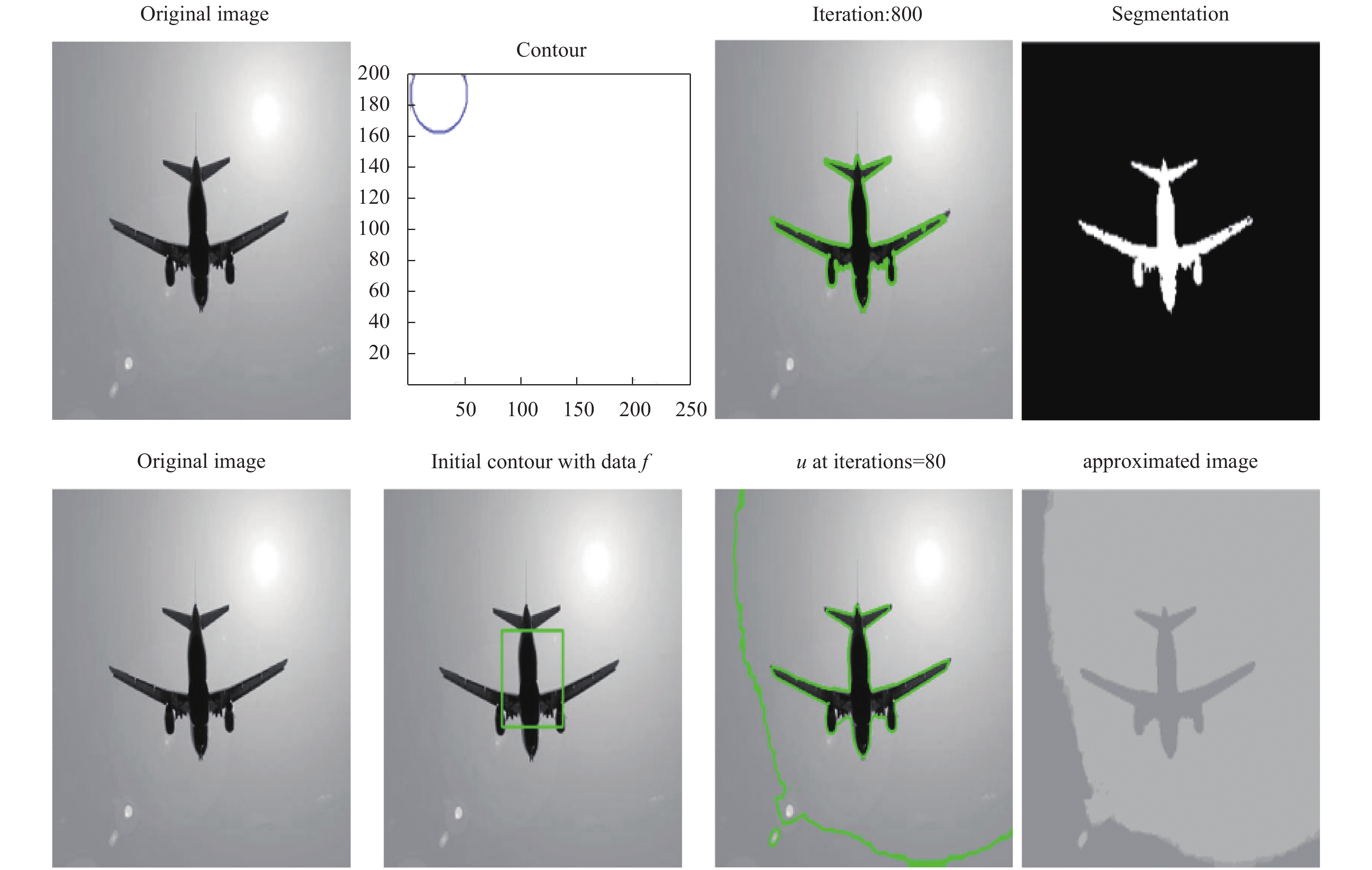
图1为CV模型和新模型对飞机图像的分割效果图, 其中, 第一, 二行分别代表CV模型和高阶正则模型对飞机图像的分割效果图; 第一列代表原始图像, 第二列分别代表CV模型和高阶正则模型对飞机图像的初始化轮廓; 第三列分别代表CV模型对飞机图像迭代800次时的边缘检测情况和高阶正则模型对飞机图像迭代80次时的边缘检测情况; 第四列分别代表CV模型对飞机图像迭代800次时的实际分割效果图和高阶正则模型对飞机图像迭代80次时的实际分割效果图.

图2表示CV模型对自然风景图像的分割效果图, 图3表示高阶正则模型对自然风景图像的分割效果图. 其中图2的4幅图分别为: 第一幅代表原始图像, 第二幅代表CV模型对自然风景图像的初始化轮廓, 第三幅代表CV模型对自然风景这幅图像迭代800次时的边缘检测图, 第四幅代表CV模型对自然风景这幅图迭代800次时的实际分割效果图. 图3的4幅图分别代表的意义为: 第一幅为原始图像, 第二幅为高阶正则模型对自然风景图像的初始化轮廓图, 第三幅图像表示高阶正则模型对自然风景图迭代200次时的边缘检测图, 第三幅图像表示高阶正则模型对自然风景图迭代200次时的实际分割效果图.

从图4可以看出, CV模型对自然风景这一幅图像迭代30次后基本收敛, 而高阶正则模型需要迭代到40次左右才收敛, 但是值得注意的是, 从两个模型对同一幅图像Loss函数曲线图可知, CV模型基本收敛后Loss函数曲线图还有小幅度跳跃情况, 然而, 高阶正则模型收敛后Loss函数曲线图相对更平滑, 说明其分割效果也很好, 更能精确地逼近物体边界.

下面我们给出一个例子说明该高阶正则模型在医学图像领域的应用, 图像分割在医学图像领域的应用就是通过发展大量的自动或者半自动图像分割方法, 精准分割医学图像, 从而替代医生的大量手工标注, 从而使得医生从大量繁重的体力劳动中解放出来.

我们用本模型在病人肺部CT图上做分割实验, 如图5所示, 从其分割效果图得知, 高模型不仅能对病人肺部做精准分割, CV模型和高阶正则模型Loss函数曲线收敛图如图6, 可知, 新模型Loss函数曲线图相对CV模型而言相对较光滑, 这更能说明该模型比CV模型来更能精确地逼近物体边界.

需要说明的是, 在分割过程中, CV模型的模型参数设置均为原始论文的参数, 考虑到CV模型的数据项数拟合高斯噪声, 而本文所设计的模型数据保真项模拟的是外加噪声, 所以, 在实验过程中, 对于CV模型而言, 并没有人工地加入任何噪声. 但是, 对于高阶正则模型而言, 由于本文假设其成像过程中可能含有外加噪声(如: 椒盐噪声), 所以在实验过程中我们用Matlab中的加噪声函数imnoise (Im0, 'salt & pepper' 0.6); 每幅原始图像都人为的加了参数为0.6的椒盐噪声. 新模型对所有图像分割的迭代总次数均设置为200, CV迭代总次数均设为800, 迭代停止条件为stoppling_tol=–10, $\lambda = 20$ , $\alpha = \beta = 1$ , ${\eta _1} = {\eta _2} = $ 50, ${\gamma _1} = {\gamma _1} = 50$ .

6 总结与展望

本文提出一个修改的Chan-Vese模型, 并引入高阶正则函数对目标函数进行惩罚, 然后对新模型用ADMM或者Split Bregmen迭代算法进行数值求解. 再者, 本文还分析了该模型的数学性质, 并给出该模型的部分收敛性分析, 实验结果表明, 通过引入高阶正则函数后, 该模型不仅能分割对比对低的物体, 而且还可以探测带噪声的物体. 大量实验表明, 该算法在各领域具有广泛应用价值, 在未来的工作中, 我们会综合一些深度学习的模块, 去探测物体的landmarks点, 从而使得算法更自动, 更鲁棒.