在雷达组网中, 雷达系统误差估计是多传感器多目标跟踪的首要问题, 与航迹关联互为前提^[1]. 雷达观测系统的测量误差主要包括两种形式的误差: 随机误差和系统误差. 随机误差可以采用各种滤波方法进行滤除^[2,3]. 系统误差是一种确定型误差, 很难通过滤波方法处理, 需要先对它进行估计, 再利用估计值对雷达量测进行补偿或配准, 才能够降低或消除其影响^[1]. 系统误差的存在会降低跟踪结果的精度, 导致跟踪均方根误差比理论值大很多; 严重时导致来自同一目标的多雷达量测关联失败, 甚至产生多条轨迹, 从而难以形成统一、准确的跟踪态势. 因此在雷达组网中, 如何解决雷达系统误差估计问题是多传感器多目标跟踪领域的重点和难点之一.

现有方法一般假设雷达系统误差为固定值, 主要包括实时精度控制(RTQC)算法、最小二乘(LS)算法、广义最小二乘(GLS)算法、基于地心地固坐标系的GLS算法(EFEC-GLS)、极大似然(ML)算法、扩维(ED)算法, 以及它们的改进方法^{[1, 4–12]}. 在实际雷达组网中存在以下特点: (1)不同雷达的系统误差一般不同, 甚至相差很大; (2)雷达探测距离越远, 测量误差越大; (3)由于不同雷达的采样时刻不同, 采样周期(或采样间隔)较大, 考虑到目标飞行速度快以及目标运动轨迹的不确定性, 导致对雷达航迹进行时间校正时, 往往会引入新的误差. 因此, 在实际中雷达量测数据包含的测量误差一般会比较大. 在这种情况下, 由于上述估计方法大多是建立在最小二乘模型上, 在计算过程中忽略了系统误差二阶或高阶项的影响, 会一定程度上降低这些方法的估计效果.

实际上, 如果已知目标的真实位置, 那么雷达系统误差估计过程将被大大简化^[13]. ADS-B(广播式自动相关)设备以GPS(全球定位系统)为基础, 能够为合作目标提供精确的位置信息, 其定位精度相对雷达量测而言完全可以近似作为目标的真实位置, 而且其采样时刻更密集^[14]. 考虑到ADS-B的优点, 文献[15]从图形学的角度, 提出一种基于多直线融合的雷达标定误差(FL)算法. 尽管FL方法简单实用, 但是其估计精度还有待进一步提高. 文献[12]基于ADS-B量测数据, 针对雷达和ADS-B跟踪平台, 提出一种联合系统误差估计方法, 但是算法复杂度依然比较高.

为此, 本文针对两坐标雷达和ADS-B联合跟踪平台, 在文献[15]的基础上, 考虑到传统基于LS模型的系统误差估计方法对量测数据比较敏感的特点, 提出一种联合ADS-B的最小二乘雷达系统误差估计方法. 提出方法首先针对雷达量测和ADS-B量测数据的特点进行预处理, 然后利用LS算法估计雷达系统误差, 最后采用实测数据实验对提出方法的有效性和可行性进行验证.

1 雷达及ADS-B航迹数预处理

考虑到雷达航迹和ADS-B航迹的坐标系(分别采用雷达局部坐标系和地理坐标系)、采样时刻不同的影响, 首先需要对它们进行预处理.

1.1 坐标转换

由于ADS-B量测数据采用地理坐标, 为了对雷达和ADS-B的量测数据进行统一处理, 需要先将ADS-B量测数据转换到以雷达为中心的局部直角坐标系. 设 $({\lambda _{A,i}},{\phi _{A,i}},{h_{A,i}})$ 是ADS-B量测的地理坐标, 则对应的局部坐标为:

$\begin{split} &{[{x_{A,i}},{y_{A,i}},{z_{A,i}}]^{\rm{T}}} =\\ &\quad\quad D({\lambda _R},{\phi _R})\left[ {P({\lambda _{A,i}},{\phi _{A,i}},{h_{A,i}}) - P({\lambda _R},{\phi _R},{h_R})} \right]\end{split}$

(1)

这里, $({\lambda _R},{\phi _R},{h_R})$ 是雷达位置的地理坐标, $D({\lambda _R},{\phi _R})$ 、 $P({\lambda _R},{\phi _R},{h_R})$ 可以分别由下面两式计算:

$D({\lambda _R},{\phi _R}) = \left[ {\begin{array}{*{20}{c}} { - \sin {\lambda _R}}&{\cos {\lambda _R}}&0 \\ { - \sin {\phi _R}\cos {\lambda _R}}&{ - \sin {\phi _R}\sin {\lambda _R}}&{\cos {\phi _R}} \\ {\cos {\phi _R}\cos {\lambda _R}}&{\cos {\phi _R}\sin {\lambda _R}}&{\sin {\phi _R}} \end{array}} \right]$

(2)

$P(\lambda ,\phi ,h) = \left[ {\begin{array}{*{20}{c}} {(N + h)\cos \phi \cos \lambda } \\ {(N + h)\cos \phi \sin \lambda } \\ {N[(1 - {\rho ^2}) + h]\sin \phi } \end{array}} \right]$

(3)

其中, $N = {{{R_e}}/{\sqrt {1 - {\rho ^2}{{\sin }^2}\varphi } }}$ , $\rho = \sqrt {1 - {{r_e^2}/{R_e^2}}} $ 为地球的偏心率, ${r_e} $ =6356.752 km为地球短轴半径, ${R_e} = $ 6378.137 km为地球长轴半径.

由于两坐标雷达仅能获取目标的斜距离和方位角信息, 后续有些步骤还需要在雷达极坐标系处理数据, 因此需要将ADS-B量测数据从雷达直角坐转换成极坐标. 设 $({r_{A,i}},{\theta _{A,i}},{h_{A,i}})$ 和 $({x_{A,i}},{y_{A,i}},{z_{A,i}})$ 分别是ADS-B量测在雷达局部坐标系中的极坐标和直角坐标, 则

$\left\{ {\begin{array}{*{20}{c}} {{r_{A,i}} = \sqrt {x_{A,i}^2 + y_{A,i}^2 + z_{A,i}^2} } \\ {{\theta _{A,i}} = \arctan ({{{x_{A,i}}}/{{y_{A,i}}}})} \\ {{h_{A,i}} = {z_{A,i}}} \end{array}} \right.$

(4)

这里主要是针对两坐标雷达量测的斜距离和方位角进行配准, 因而只需要对雷达量测和ADS-B量测的斜距离和方位角进行处理. 为了后续处理方便, 仍需进一步将雷达量测和ADS-B量测转换到平面直角坐标系, 设 $({x'_i},{y'_i})$ 和 $({r_i},{\theta _i})$ 分别为雷达量测或ADS-B量测的极坐标和直角坐标, 则

$\left\{ {\begin{array}{*{20}{c}} {{{x'}_i} = {r_i}\sin {\theta _i}} \\ {{{y'}_i} = {r_i}\cos {\theta _i}} \end{array}} \right.$

(5)

在下文中, 涉及的雷达量测或ADS-B量测的直角坐标均是通过式(5)计算得到.

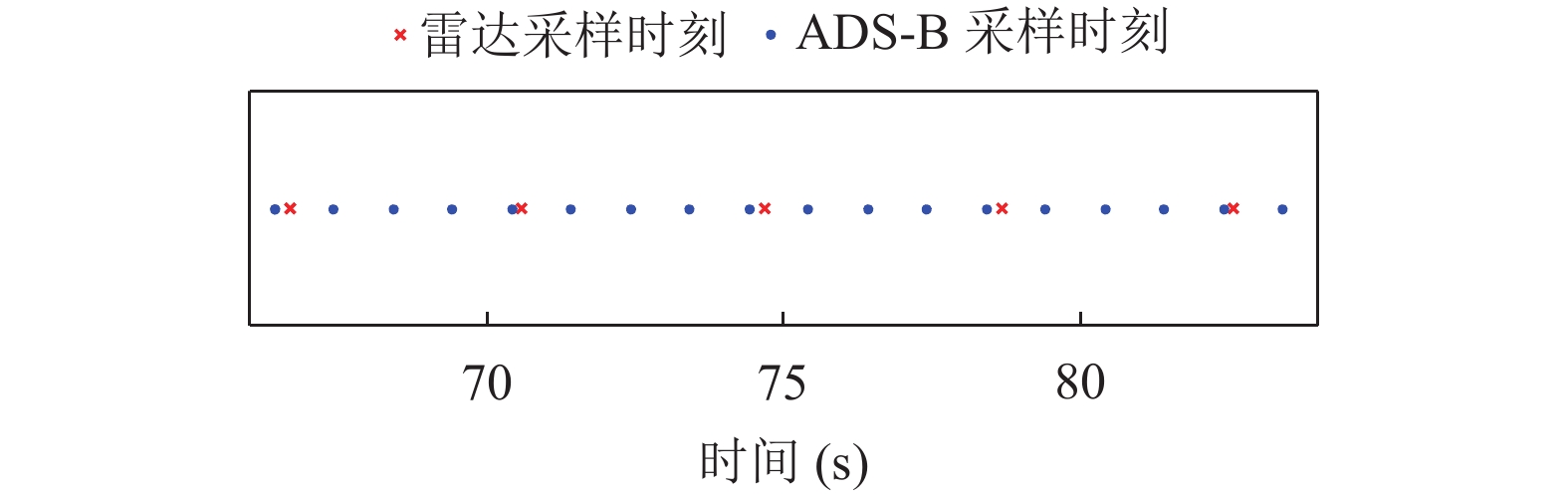
1.2 时间配准

在实际中, 雷达和ADS-B对目标进行个跟踪时, 采样时刻只是近似周期的. 一般地, ADS-B采样时刻比雷达更密集. 图1给出实际中雷达和ADS-B跟踪同一批目标的采样时刻, 可以看出ADS-B采样间隔比雷达更小、更密集. 为了方便进一步对雷达数据处理以及更准确地估计雷达系统误差, 这里以雷达航迹数据的采样时刻序列 $\{ {t_{R,i}}\} _{i = 1}^M$ 为基准, 对ADS-B航迹数据进行插值, 通过计算得到的插值序列作为新的ADS-B航迹数据, 用于估计雷达系统误差.

在具体插值过程中, 由于ADS-B采样间隔小, 近似1s/次, 为此可以假设目标在单个采样间隔做匀速运动, 采用与雷达采样时刻 ${t_{R,i}}$ 相邻的两个ADS-B量测 ${z_{A,j}}$ 、 ${z_{A,j + 1}}$ ( ${t_{A,j}} < {t_{R,i}} < {t_{A,j + 1}}$ )计算插值:

$\left\{ {\begin{array}{*{20}{c}} {{{\hat x}_{A,i}} = {x_{A,j}} + {{\hat v}_{x,i}}({t_{A,j + 1}} - {t_{R,i}})} \\ {{{\hat y}_{A,i}} = {y_{A,j}} + {{\hat v}_{y,i}}({t_{A,j + 1}} - {t_{R,i}})} \end{array}} \right.$

(6)

其中,

$\left\{ {\begin{array}{*{20}{c}} {{{\hat v}_{x,i}} = {{({x_{A,j + 1}} - {x_{A,j}})}/{({t_{A,j + 1}} - {t_{A,j}})}}} \\ {{{\hat v}_{y,i}} = {{({y_{A,j + 1}} - {y_{A,j}})}/{({t_{A,j + 1}} - {t_{A,j}})}}} \end{array}} \right.$

(7)

式中, ${t_{A,j}}$ 、 ${t_{A,j + 1}}$ 为对应 ${z_{A,j}}$ 、 ${z_{A,j + 1}}$ 的采样时刻.

1.3 雷达方位角误差补偿

考虑到系统误差估计算法对量测误差比较敏感, 为了更准确地估计雷达系统误差, 这里首先估计雷达方位角误差的粗值, 然后对雷达方位角数据进行补偿. 假设目标做直线运动, 采用最小二乘拟合计算雷达航迹和ADS-B航迹对应的直线方程:

$\left\{ {\begin{array}{*{20}{c}} {{{\hat l}_R}:{y_{R,i}} = {{\hat a}_R}{x_{R,i}} + {{\hat b}_R}} \\ {{{\hat l}_A}:{y_{A,i}} = {{\hat a}_A}{x_{A,i}} + {{\hat b}_A}} \end{array}} \right.$

(8)

然后计算两直线的夹角, 并将该夹角作为雷达方位角误差估计的粗值:

$\Delta {\hat \theta _{R,0}}{\rm{ = }}\arctan \left| {\frac{{{{\hat a}_R} - {{\hat a}_A}}}{{1 + {{\hat a}_R}{{\hat a}_A}}}} \right|$

(9)

最后利用该粗值补偿雷达航迹的方位角数据:

${\theta '_{R,i}} = {\theta _{R,i}} + \Delta {\theta _{R,0}}$

(10)

2 基于最小二乘的雷达系统误差估计

设雷达航迹数据和ADS-B航迹数据经过预处理后, $({r_{R,i}},{\theta _{R,i}})$ 和 $({r_{A,i}},{\theta _{A,i}})$ 分别表示 ${t_i}$ 时刻目标 $T$ 在雷达极坐标系中的雷达量测和ADS-B量测的极坐标, $({x'_{R,i}},{y'_{R,i}})$ 和 $({x'_{A,i}},{y'_{A,i}})$ 分别为它们在雷达直角坐标系中直角坐标, $\Delta {r_R}$ 、 $\Delta {\theta _R}$ 分别是雷达的斜距离系统误差和方位角系统误差. 如果忽略随量测误差的影响, 根据(5)式可以得到:

$\left\{ {\begin{array}{*{20}{c}} {{{x'}_{R,i}} = ({r_{R,i}} - \Delta {r_R})\sin ({\theta _{R,i}} - \Delta {\theta _R})} \\ {{{y'}_{R,i}} = ({r_{R,i}} - \Delta {r_R})\cos ({\theta _{R,i}} - \Delta {\theta _R})} \end{array}} \right.$

(11)

因为 $\Delta {r_R}$ 、 $\Delta {\theta _R}$ 是微量, 若忽略它们的二阶项, 式(11)可以简化为:

$\left\{ {\begin{array}{*{20}{c}} {{{x'}_{R,i}} = {r_{R,i}}\sin {\theta _{R,i}} - \Delta {r_R}\sin {\theta _{R,i}} - \Delta {\theta _R}{r_{R,i}}\cos {\theta _{R,i}}} \\ {{{y'}_{R,i}} = {r_{R,i}}\cos {\theta _{R,i}} - \Delta {r_R}\sin {\theta _{R,i}} + \Delta {\theta _R}{r_{R,i}}\sin {\theta _{R,i}}} \end{array}} \right.$

(12)

考虑到ADS-B系统误差相对雷达系统误差非常小, 这里忽略ADS-B系统误差, 将其近似作为目标位置的真实位置, 即:

$\left\{ {\begin{array}{*{20}{c}} {{{x'}_{A,i}} = {r_{A,i}}\sin {\theta _{A,i}}} \\ {{{y'}_{A,i}} = {r_{A,i}}\cos {\theta _{A,i}}} \end{array}} \right.$

(13)

由 $({x'_{R,i}},{y'_{R,i}})$ 和 $({x'_{A,i}},{y'_{A,i}})$ 的几何关系可知:

$\left\{ {\begin{array}{*{20}{c}} {{r_{R,i}}\sin {\theta _{R,i}} - \Delta {r_R}\sin {\theta _{R,i}} - \Delta {\theta _R}{r_{R,i}}\cos {\theta _{R,i}}{\rm{ = }}{r_{A,i}}\sin {\theta _{A,i}}} \\ {{r_{R,i}}\cos {\theta _{R,i}} - \Delta {r_R}\sin {\theta _{R,i}} + \Delta {\theta _R}{r_{R,i}}\sin {\theta _{R,i}}{\rm{ = }}{r_{A,i}}\cos {\theta _{A,i}}} \end{array}} \right.$

(14)

通过恒等式变形可以得到:

$\left\{ {\begin{array}{*{20}{c}} {{r_{R,i}}\sin {\theta _{R,i}} - {r_{A,i}}\sin {\theta _{A,i}}{\rm{ = }}\Delta {r_R}\sin {\theta _{R,i}} + \Delta {\theta _R}{r_{R,i}}\cos {\theta _{R,i}}} \\ {{r_{R,i}}\cos {\theta _{R,i}} - {r_{A,i}}\sin {\theta _{A,i}}{\rm{ = }}\Delta {r_R}\sin {\theta _{R,i}} - \Delta {\theta _R}{r_{R,i}}\sin {\theta _{R,i}}} \end{array}} \right.$

(15)

令 ${Z_i} = \left[ {\begin{array}{*{20}{c}} {{r_{R,i}}\sin {\theta _{R,i}} - {r_{A,i}}\sin {\theta _{A,i}}} \\ {{r_{R,i}}\cos {\theta _{R,i}} - {r_{A,i}}\sin {\theta _{A,i}}} \end{array}} \right]$ , $\beta = {[\Delta {r_R},\Delta {\theta _R}]^{\rm{T}}}$ , ${H_i} = \left[ {\begin{array}{*{20}{c}} {\sin {\theta _{R,i}}}&{{r_{R,i}}\cos {\theta _{R,i}}} \\ {\cos {\theta _{R,i}}}&{ - {r_{R,i}}\sin {\theta _{R,i}}} \end{array}} \right]$ , 则式(15)用矩阵的形式可以进一步表示为:

${Z_i}{\rm{ = }}{H_i}\beta $

(16)

针对雷达航迹 $M$ 个不同的量测数据, 根据(16)式可得:

${\left[ {{Z_1},{Z_2}, \cdots, {H_M}} \right]^{\rm{T}}}{\rm{ = }}{\left[ {{H_1},{H_2}, \cdots, {H_M}} \right]^{\rm{T}}}\beta $

(17)

令 $H = {\left[ {{H_1},{H_2}, \cdots, {H_M}} \right]^{\rm{T}}}$ , $Z{\rm{ = }}{\left[ {{Z_1},{Z_2}, \cdots, {Z_M}} \right]^{\rm{T}}}$ , 则式(17)可以进一步表示为:

$Z{\rm{ = }}H\beta $

(18)

由于式(18)是超定的, 可以采用最小二乘估计方法^[16]求解可得:

$\beta {\rm{ = }}({H^{\rm{T}}}{H^{ - 1}}){H^{\rm{T}}}Z$

(19)

3 实测数据实验

为了验证提出方法的性能, 采用实测数据对三种系统误差方法进行比较, 包括基于直线拟合的系统误差估计方法(FL)、基于最小二乘的系统误差估计方法(LS)、以及基于直线拟合的最小二乘系统误差估计方法(FL-LS).

实测数据来源于空中同一批合作目标的雷达航迹和ADS-B航迹的量测数据, 目标在空中近似做直线运动, 如图2所示. 其中, 雷达航迹包括27个采样点, ADS-B航迹包括105个采样点. 为了估计雷达系统误差, 首先将ADS-B航迹数据从地理坐标系转换到雷达的局部坐标系, 并将雷达航迹数据从雷达极坐标系转换到雷达直角坐标系.

经过转换后的雷达航迹和ADS-B航迹的量测数据如图2所示. 由图2可知, 尽管存在系统误差, 但是雷达航迹和ADS-B航迹的量测数据都近似分布于所对应直线的两侧, 特别是ADS-B航迹. 这是因为ADS-B数据集以GPS为基础, 定位精度高, 能够满足雷达对系统误差估计的要求^[15]. 因此, 可以通过计算雷达航迹和ADS-B航迹对应直线的夹角, 将其作为雷达方位角系统误差估计的粗值, 用于补偿雷达航迹数据的方位角. 由图2可以看出, ADS-B航迹采样时刻比雷达更密集. 为了对雷达航迹进行配准, 需要以雷达航迹数据的采样时刻为基准, 计算ADS-B航迹在对应时刻的插值, 再利用计算得到的插值序列构建新的ADS-B航迹数据, 用于估计雷达系统误差. 经过插值处理后, 新的ADS-B航迹与雷达航迹的采样时刻相同, 采样点数也为27个.

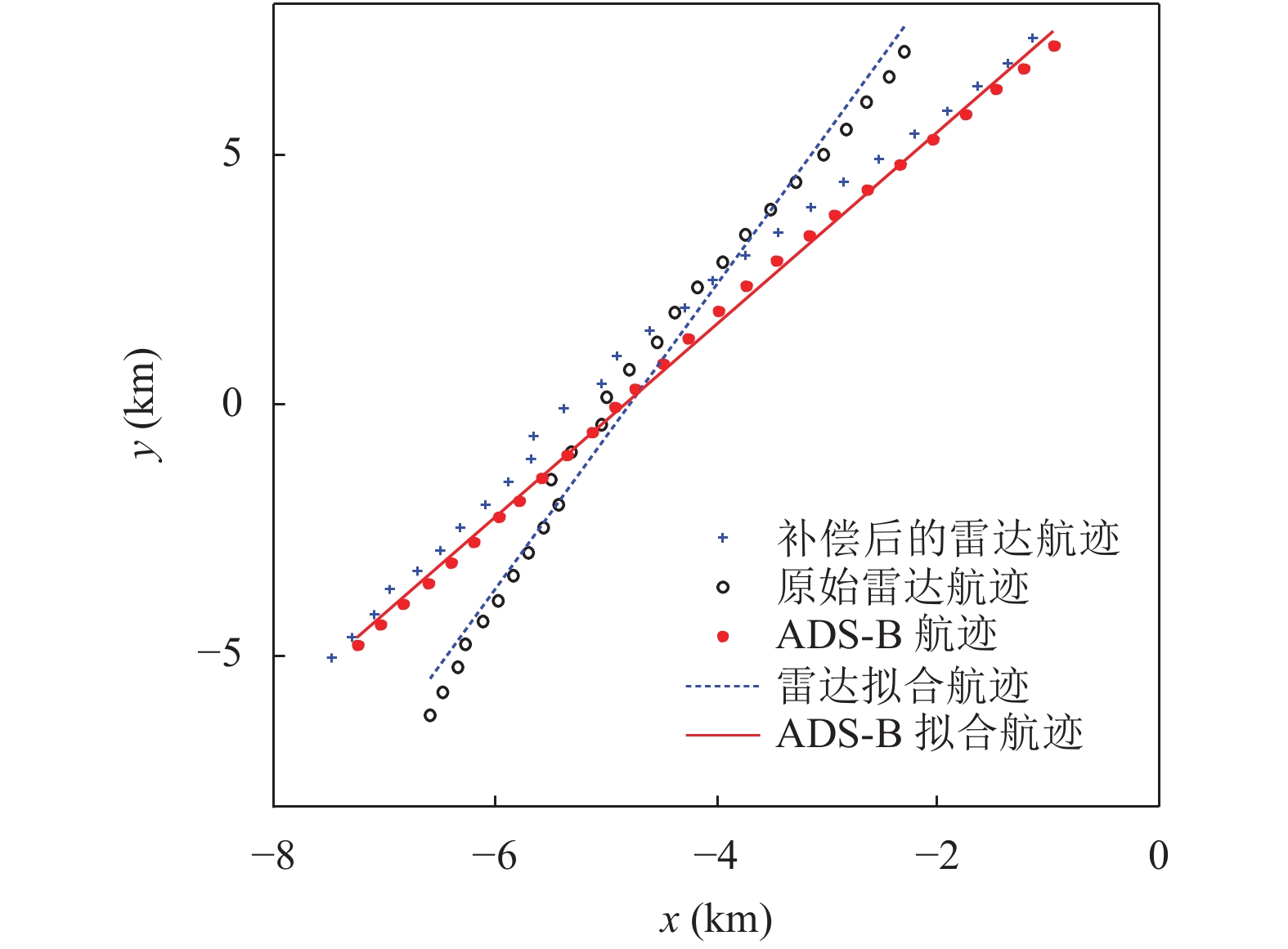
图3给出经过时间插值的新ADS-B航迹和雷达航迹数据, 以及对新ADS-B航迹数据和雷达航迹数据的拟合直线. 经过直线拟合后, 可以计算得到两条直线的夹角为161.7 mrad, 用于补偿雷达航迹数据的方位角, 经过方位角补偿后的新雷达航迹数据也如图3所示. 由图3可知, 对于雷达航迹和ADS-B航迹, 都近似分布于拟合直线的两侧, 经过方位角补偿的雷达航迹数据在平面直角坐系中更接近ADS-B航迹.

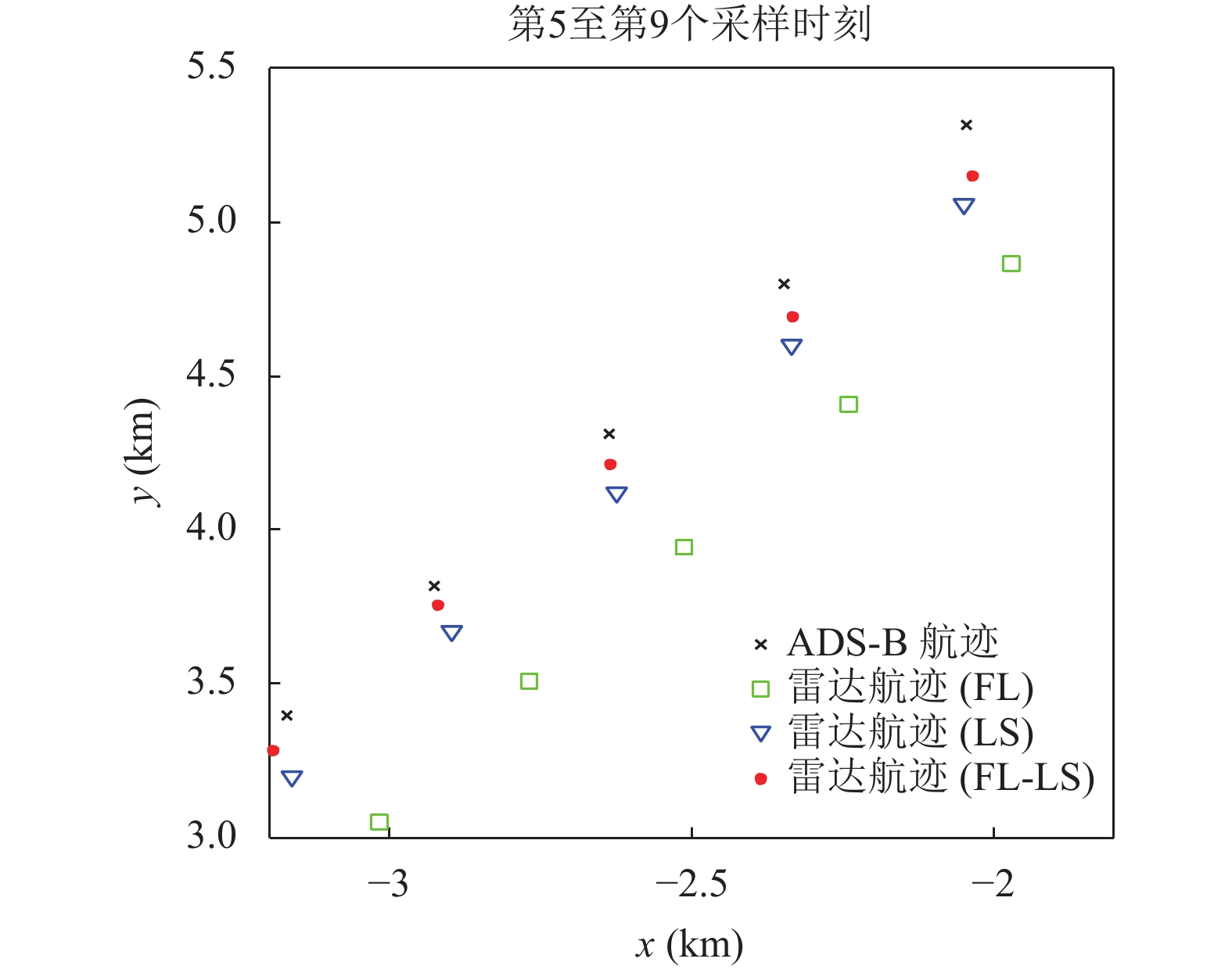
图4是采用系统误差配准后的雷达航迹. 由图4可知, 采用FL、LS以及FL-LS三种估计方法配准后的雷达航迹都十分接近ADS-B航迹, 证明三种系统误差估计方法都是有效的. 为了更好地说明三种方法的性能, 图5列举了第5至第9个采样时刻的三种雷达航迹的量测数据. 从图5可知, 按照到ADS-B航迹点距离从小到大依次是分别是经由FL-LS、LS和FL配准后的雷达航迹, 从而说明FL-LS方法的估计精度最高, 其次是LS方法, 最后是FL方法.

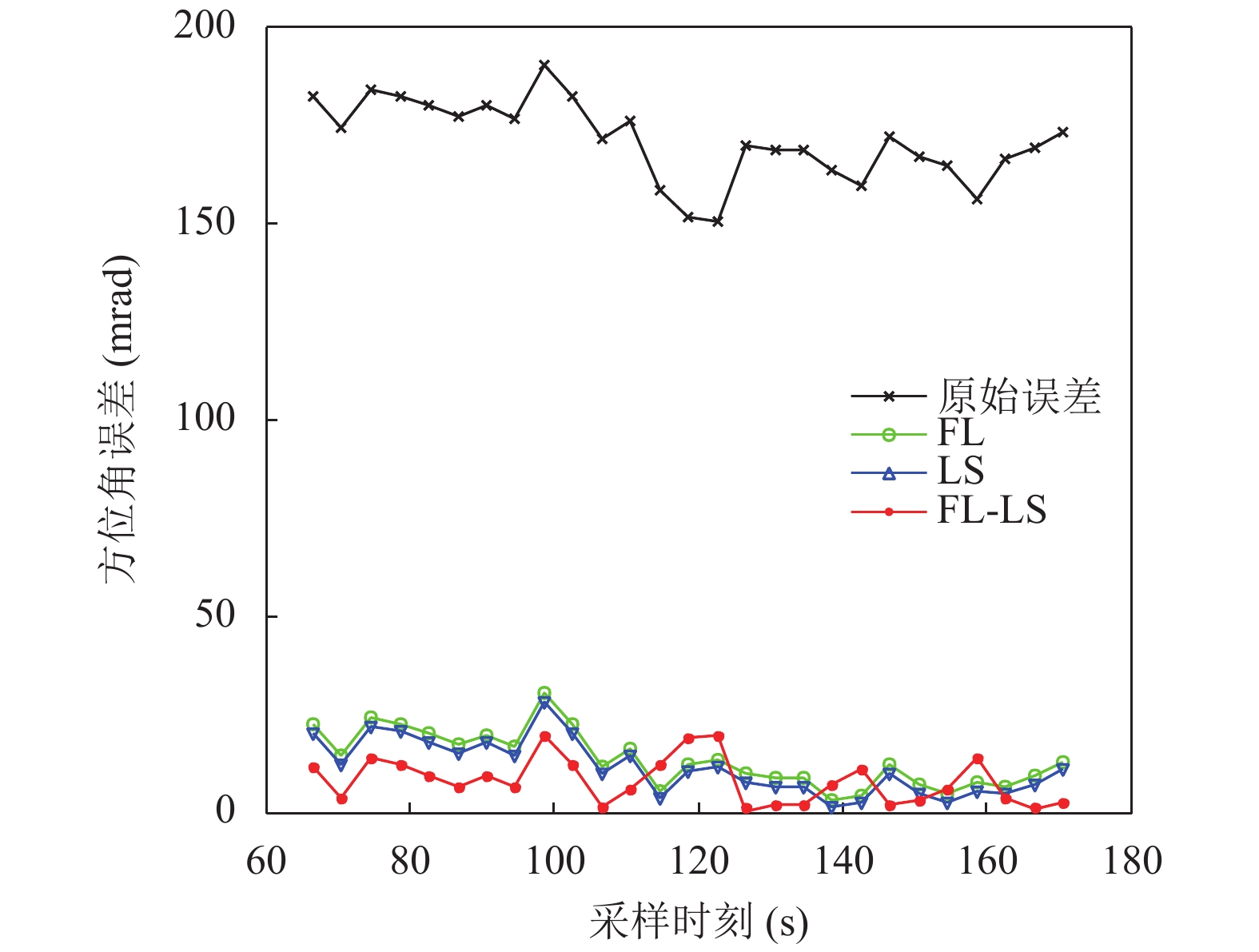
为了更直观地比较三种方法的性能, 图6和图7分别给出三种配准后雷达航迹在每一时刻斜距离估计误差和方位角估计误差. 由图6可知, 在大部分采样时刻, FL-LS方法的斜距离配准效果要优于LS方法和FL方法, 而LS方法又要优于FL方法. 类似地, 由图7也可以得到同样的结论, 方位角配准性能从低到高依次是: FL方法、LS方法和FL-LS方法. 三种估计方法均较大地降低了方位角误差. 特别地, 尽管FL方法方位角估计结果比LS方法略差, 但已十分接近, 从而也说明从图形学的角度分析和估计雷达系统误差也是一种简单、有效的方法, 为以后进一步分析雷达系统误差估计问题提供了一种很好的解决思路.

最后, 表1给出了三种系统误差估计的结果, 表2给出配准后雷达航迹的平均误差(以ADS-B航迹数据为真值). 与上述系统误差性能的分析结果类似, 由表2可知, 无论是在斜距离还是方位角上, 三种估计方法的性能从高到低依次是FL-LS方法、LS方法和FL方法. 针对方位角误差, 三种系统误差估计方法都能较大地提高雷达航迹的方位角的精度. 为了定量说明配准后雷达航迹的精度情况, 分别定义斜距离配准性能指标和方位角配准性能指标:

$\left\{ {\begin{array}{*{20}{c}} {{\eta _r} = \dfrac{{{\varepsilon _{r0}} - {\varepsilon _r}}}{{{\varepsilon _{r0}}}} \times 100{\rm{\% }}} \\ {{\eta _\theta } = \dfrac{{{\varepsilon _{\theta 0}} - {\varepsilon _\theta }}}{{{\varepsilon _{\theta 0}}}} \times 100{\rm{\% }}} \end{array}} \right.$

(20)

其中, ${\varepsilon _r}$ 、 ${\varepsilon _{r0}}$ 分别为配准后雷达航迹的斜距离平均误差和配准前雷达航迹的平均误差, ${\varepsilon _\theta }$ 、 ${\varepsilon _{\theta 0}}$ 分别为配准后雷达航迹的方位角平均误差和配准前雷达航迹的方位角平均误差, ${\eta _r}$ 、 ${\eta _\theta }$ 定义为配准性能指标.

在此基础上, 表3给出了三种估计方法的配准性能指标情况, 从而能够定量地分析它们的配准性能. 由表3可知, 经过配准处理后, FL-LS方法、LS方法能够较大地降低雷达航迹的斜距离平均误差, 且FL-LS方法优于LS方法, 斜距离平均距离误差降低了71.7%. FL方法对雷达航迹的斜距离平均误差改善不明显, 效果不好, 仅降低0.2%. 另外, 三种方法都能较大地降低雷达航迹的方位角平均误差, 其中FL-LS方法最好, 其次是LS方法, 最后是FL方法. FL方法对雷达航迹的方位角平均误差降低了52.7%. 因此, 无论是对斜距离还是方位角, FL-LS方法的配准性能均是最好.

4 结束语

本文首先分析了传统系统误差配准方法的优点和不足. 在此基础上, 针对两坐标雷达系统误差估计问题, 提出一种联合ADS-B的最小二乘雷达系统误差估计方法. 在提出方法中, 首先对雷达航迹和ADS-B航迹的量测数据进行预处理, 包括通过坐标转换建立统一的配准空间, 采用插值方法构造新的ADS-B航迹, 以及对雷达航迹数据的航向角进行补偿. 经过预处理后, 能够一定程度上降低雷达量测数据的误差. 然后, 采用最小二乘算法估计雷达系统误差. 通过实测数据实验结果证明, 相对传统直线拟合方法和最小二乘方法, 提出方法能够更有效、更准确地估计雷达系统误差. 经过提出方法配准处理后, 雷达航迹数据的平均斜距离误差和方位角误差分别降低了71.7%和52.7%.

在下一步工作中, 我们将考虑目标运动、以及雷达和ADS-B采样时间的不确定等因素, 并结合实测数据, 对ADS-B的雷达系统误差估计问题进一步分析和研究, 从而更准确地估计雷达系统误差. 特别是针对目标非直线航迹数据的情况, 对本文提出方法进行改进, 以提高方法的鲁棒性.