随着生活水平的不断提高, 人们对眼睛的保护意识越来越强. 裂隙灯显微镜, 如图1, 作为医院检查眼睛病状最重要的设备, 医院对裂隙灯显微镜成像质量的要求也越来越高. 而裂隙灯显微镜中对最终成像质量起关键性作用的的结构就是转鼓, 如图2.
在传统转鼓装校平台上, 如图3, 主要依靠工人师傅主观判断转鼓在显示器上所呈现图像的清晰度来评价转鼓装校的优劣, 如图4. 由于每个工人师傅的主观感受不一, 长时间工作导致的视觉疲劳, 传统方法存在着随机性、不准确性、效率低下、有损视力等一系列问题, 本文提出一种基于改进的清晰度评价算法的裂隙灯转鼓数字化装校方法, 以实现依靠CCD相机拍摄转鼓图像后, 自动进行图像清晰度判别, 从而反映每组镜片装校的优劣.

|
图 1 裂隙灯显微镜 |

|
图 2 转鼓 |

|
图 3 传统装校平台 |
裂隙灯转鼓数字化装校方法的难点在于选择合适图像预处理方式, 筛选出一种适合于转鼓图像使用的清晰度评价算法, 并设计一套软件对转鼓图像进行实时评价. 以求在生产线上能够更加快速, 准确的装校裂隙灯转鼓, 提高裂隙灯质量, 提升产品竞争力[1].

|
图 4 传统图像评价工具 |
1 转鼓图像清晰度评价方法
相较于装校不合格转鼓, 合格的转鼓呈现的图像细节更丰富, 在空域表现为相邻像素的灰度值变化较大, 在频域表现为频谱的高频分量多, 对比度也更加强烈.
常用的图像清晰度评价算法主要可分为3类[2–5]: ① 全参考质量评价(Full Reference QA), 将需要检测的图像和标准的参考图像进行比较, 从而得到清晰度评价结果, 此类算法有PSNR、SSIM、MSSIM、IFC、VIF、FSIM等算法;② 弱参考质量评价(Reduced Reference QA), 先从标准的参考图像中得到一些有用的特征信息, 再利用这些特征信息对需要检测的图像清晰度进行计算评价;③ 无参考质量评价(No Reference QA), 不需要任何标准参考图像的辅助, 只依靠算法本身独立完成对需要检测图像的清晰度的评价. 无参考图像质量评价算法在计算评价时, 只分析自身图像的特点, 因此不需要先获取无失真的标准参考图像.
无参考图像清晰度评价方法主要包括空域算法、频域算法和统计学算法三类.
1.1 基于空域的梯度函数算法在空域算法中, 清晰的图像相比于模糊的图像表现为边缘和细节更加清晰, 边缘相邻像素的特征值(如灰度)变化较大, 所以主要依据边缘检测算子, 通过计算图像的灰度梯度差来表征待测图像的清晰程度.
(1) Brenner算法
传统Brenner算法[6,7]以Brenner算子作为基础, 该算法只计算相差两个像素单元的两个图像像素的灰度差, 由于需要对图像轮廓的贡献进行增强, 所以对差值进行了平方处理, 从而使用差值平方的和作为图像清晰度的评价值. 一幅高宽为
| ${F_{\rm{Brenner}}} = \sum\limits_M {\sum\limits_N {{{(f(x + 2,y) - f(x,y))}^2}}} $ | (1) |
式中, (f(x+2, y)–f(x, y)2)(自定义阈值), f(x, y)是像素点(x, y)的灰度值, FBrenner为图像清晰度计算结果(下同).
根据Brenner算法的定义, 装校合格的转鼓显示的图像具有最大的计算值. 在实际的清晰度评价软件应用中, Brenner算法只统计大于一定阈值的灰度差, 而舍弃掉小于阈值的灰度差. 因此, 阈值选取是否合适直接关系到该算法的准确性, 一个好的阈值可以很准确地评价图像的清晰度. 如果阈值选取的很低, 则Brenner算子能够计算的像素越多, 计算的结果也就越容易受到周围噪声的影响. 与此相反, 如果阈值选取的太高, 则会导致图像的细节遗失过多, 从而降低清晰度评价算法的计算准确性.
(2) Tenengrad算法
Tenengrad算法[8–10]由Tenenbaum提出, 是一种常用的图像清晰度评价方法. 在处理过程中, 该算法使用Sobel算子提取图像水平方向和竖直方向的梯度值. 并将处理后的梯度值之和作为图像清晰度评价值. 其定义如下:
| ${T_{\rm{Tenengrad}}} = \sum\limits_M {\sum\limits_N {\left| {G(x,y)} \right|}} $ | (2) |
| $G(x,y) = \sqrt {G_x^2(x,y) + G_y^2(x,y)} $ | (3) |
式中, G(x, y)>T, Gx和Gy分别是Sobel算子在像素点(x, y)处的水平方向和竖直方向的卷积. 使用以下的Sobel算子模板:
| ${g_x} = \frac{1}{4}\left[ {\begin{array}{*{20}{c}} { - 1}&0&1 \\ { - 2}&0&2 \\ { - 1}&0&1 \end{array}} \right],\;{g_y} = \frac{1}{4}\left[ {\begin{array}{*{20}{c}} 1&2&1 \\ 0&0&0 \\ { - 1}&2&{ - 1} \end{array}} \right] $ | (4) |
Tenengrad算法具有单峰性好、可靠性高等特点.
(3) Laplacian算法
Laplacian算法利用Laplacian算子对图像进行模板卷积, 从而得到图像的高频分量, 然后对图像的高频分量求和, 用高频分量之和作为图像清晰度评价值. 其定义如下:
| ${F_{{\rm{Laplacian}}}} = \sum\limits_M {\sum\limits_N {\left| {G(x,y)} \right|} } $ | (5) |
式中, G(x, y)>T, G(x, y)是Laplacian算子在像素点(x, y)处的卷积. 使用以下Laplacian算子模板:
| $L = \frac{1}{6}\left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 1&{ - 4}&1 \\ 0&1&0 \end{array}} \right] $ | (6) |
(4) SMD算法
SMD (Sum of Modulus of gray Difference, 相邻像素灰度方差法, 简称灰度方差)算法[11], 对像素点(x, y)及其邻近点的灰度作差分运算, 用图像灰度差分绝对值之和作为图像清晰度评价值. 其定义为:
| ${F_{\rm{SMD}}} = \sum\limits_M {\sum\limits_N {\left( \begin{array}{l} \left| {f(x,y) - f(x,y - 1)} \right| \\ + \left| {f(x,y) - f(x + 1,y)} \right| \\ \end{array} \right)}} $ | (7) |
SMD算法具有较好的计算性能, 但同时, 该算法的缺点也非常明显, 就是在靠近焦点的附近的时候, 算法的灵敏度不是很高, 也就是说SMD算法在图像最清晰度的附近计算结果过于平坦, 变化不够明显, 从而导致聚焦精度难以提高[12].
1.2 基于频域的图像变换域算法在频域算法中, 清晰图像相比于模糊图像表现为图像的高频分量比例更大, 对比度也更强烈, 可以利用傅里叶变换、小波变换等变换方法提取待测图像的不同频率成分, 计算高频成分所占比例来表征图像清晰程度[13]. 具体处理过程: 利用傅立叶变换对转鼓图像的频率进行分析, 即对图像进行FFT变换, 其定义如下:
| $\begin{split} {F_{\rm{FFT}}} = &\frac{1}{{M \times N}}\sum {(rea{l^2} + imaginar{y^2})} \\ &\times {\tan ^{ - 1}}(imaginary/real) \\ \end{split} $ | (8) |
式中, real和imaginary分别表示图像变换后的实部和虚部, 计算结果越大表征图像的清晰度越好.
1.3 基于统计学的熵函数算法统计学算法主要利用统计学思想, 以信息量表征图像清晰程度. 基于统计特征的熵函数[14]是衡量图像 信息丰富程度的一个重要指标, 根据 Shannon 信息论, 熵最大时信息量最多, 则FShannon越大则图像越清晰, 并定义如下:
| ${F_{\rm{Shannon}}} = - \sum\limits_{i = 0}^{L - 1} {{p_i}\ln ({p_i})} $ | (9) |
式中, pi是图像中灰度值为i的像素出现的频率, L为图像的灰度级总数(常取256级). 熵函数灵敏度不高, 在图像内容不同的情况下容易出现与真实情况相反的结果.
1.4 其他算法前三类算法能够满足对特定一类图像的清晰度的评价, 但是没有和人眼视觉系统(Human Visual System HVS)相结合, 所以存在一定的局限性. 近年来, 随着人们对于HVS特性的进一步研究和深入了解, 不断引入新的图像清晰度评价方式, 如基于点锐度的清晰度算法(EVA):
EVA算法[15–17]由徐贵力等人提出, 是一种基于边缘锐度的图像清晰度评价算法. 该算法只对图像的特定边缘区域进行统计, 且在计算前需要人工选定边缘区域, 不便实现程序运算自动化. 因此王鸿南等人提出了改进的EVA算法: ① 将特定边缘梯度的计算改为逐个像素领域梯度的计算; ② 对像素8领域的灰度变化进行距离加权, 水平垂直方向为1, 45°和135°为
| ${F_{\rm{EVA}}} = \frac{\displaystyle{\sum\nolimits_M {\sum\nolimits_N {\sum\nolimits_{i = 1}^8 {\left| {df/dx} \right|} } } }}{{M \times N}} $ | (10) |
改进的算法能对图像的整体进行评价, 容易使程序实现自动化.
空域方法计算简单, 实现方便, 应用广泛, 但抗噪声性能较差, 且易受光照条件和背景干扰; 频域方法灵敏度高, 但计算量大, 一般较少采用; 统计学方法具有一定的抗噪性, 但准确率低, 灵敏度低. 在本文中选用4种空域方法和EVA算法进行实验对比研究.
2 实验分析一个好的清晰度评价函数应该满足4个要求[18,19]: ① 单峰性是指只有一个极值, 不能出现其他局部极值; ② 无偏性是指在光学系统的正焦位置, 图像清晰度评价值是调焦曲线的最大值, 也就是最大值位置恰好对应系统正焦位置, 也就是计算出来的清晰度曲线要与图像的清晰度变化事实相吻合; ③ 灵敏性是指能够区分开轻微离焦状态, 并且评价值变化梯度大使系统容易得到真实的焦平面, 即对不同程度的模糊图片, 清晰度评价结果要求有一定的差别; ④ 实时性是指运算时间小于一定阈值, 满足实际生产需要.
其中单峰性和无偏性决定了评价函数的正确性, 灵敏性决定了评价函数的准确性, 实时性决定了该程序是否能够适用于工厂中的实际生产线.
在实验过程中CCD相机获取的图像由于转鼓倍率的不断改变和现实装校过程中光照条件的非人为改变, 图像的比度和节会发生变化, 所以需要考虑不同放大倍率和不同光照条件对算法的影响; 而获取的图像内容不变, 均是十字刻线, 且获取的图像尺寸大小不变(设定为1280×960), 故不需要考虑算法计算结果与图像内容, 图像尺寸的关系. 本文设计了3组实验用于比较选取的五种算法对4个要求的符合程度.
2.1 实验软硬件配置、实验平台实验中使用的硬件和软件如下: 德国IDS公司生产的型号为UI148xLE-C的工业相机, 日本Computar公司生产的焦距为16 mm、最大光圈为F1.4、像场2/3英寸的工业镜头; 使用Visual Studio2013中的OPENCV3.0.0库进行开发; 计算机硬件配置: 处理器Core(TM)i5-7500 主频 3.40 GHz; 内存DDR4 16 GB; 显卡NVIDIA GeFoRce GTX1060 3 G.
实验平台采用IDS相机作为光电接收器件, 使用LED光源、光学透镜、导轨、光学镜座等光学元件, 搭建了如图5的转鼓装校平台.

|
图 5 转鼓装校平台 |
2.2 实验1. 单峰性、无偏性、灵敏性和实时性
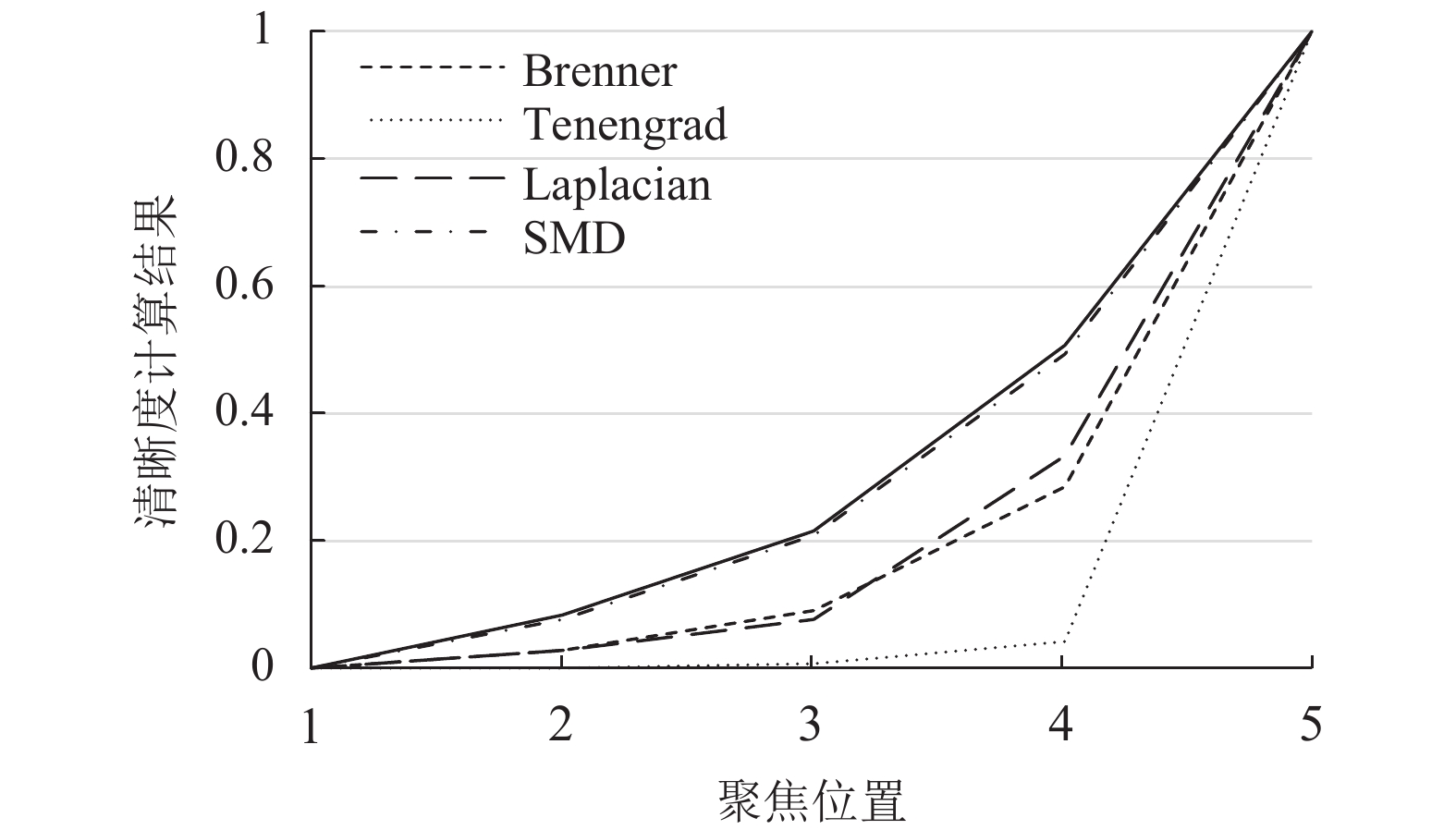
为了对比不同算法的单峰性、无偏性、灵敏性和实时性, 实验1为: 在同一放大倍率下, 同一光照条件下, 调整CCD相机焦距, 得到转鼓不同焦距下不同清晰度的图像, 如图6. 然后运行程序对5幅图像进行单独评价, 将5种算法计算得出的结果在不同尺度下进行归一化, 如图7. 算法运行时间如表1.
图7的横坐标表示不同焦距位置拍摄图像的序号, 聚焦位置由1到5人眼的主观感受逐渐清晰, 主观评价逐渐提高, 纵坐标表示不同算法下清晰度的计算结果(下同). 实验所选取的5种清晰度算法的计算结果都只在聚焦位置5处达到极值, 满足单峰性要求; 转鼓图像清晰度计算结果与人眼的主观感受的图像清晰度变化一致, 满足无偏性要求; 除Tenengrad算法外, 其余算法计算结果均不相同, 且区分度较好, 满足灵敏性要求; 表1为5种清晰度评价函数在5个聚焦位置进行50组实验的平均运行时间, 从表1可以看出每个算法对单张图片的运算时间都控制在1秒以内, 所以能够满足实时性要求.

|
图 6 不同焦距图像 |
|
图 7 不同焦距图像计算结果 |
2.3 实验2. 算法与放大倍率的无关性
为了比较5种算法计算结果与图像放大倍率的无关性, 实验2为: 在同一光照条件下, 改变裂隙灯转鼓的放大倍率并保持不变, 重复实验1中5个焦距位置, 得到不同清晰度的图像, 如图8. 然后运行程序对5幅图像进行单独评价, 将5种算法计算得出的结果在不同尺度下进行归一化, 如图9.
| 表 1 不同算法单次运行时间(单位: ms) |

|
图 8 放大图像 |

|
图 9 放大图像计算结果 |
对于实验2, 人眼的主观感受由聚焦位置1到聚焦位置5, 清晰度依次上升. 实验所选取的5种清晰度算法的计算结果都只在聚焦位置5处达到极值, 满足单峰性要求; 转鼓图像清晰度计算结果与人眼的主观感受的图像清晰度变化一致, 满足无偏性要求; 除Tenengrad算法外, 其余算法计算结果均不相同, 且区分度较好, 满足灵敏性要求; 单次运行时间与表1相差不大, 每个算法对单张图片的运算时间都控制在1秒以内, 所以能够满足实时性要求.
2.4 实验3. 算法与光照条件的无关性为了比较5种算法计算结果与图像的光照条件, 即图像亮度的无关性, 实验3为: 在同一放大倍率下, 将光源亮度改变并保持不变, 重复实验1中5个焦距位置, 得到不同清晰度的图像, 如图10. 然后将计算得出的结果在不同尺度下进行归一化, 如图11.

|
图 10 亮度增强图像 |
对于实验3, 人眼的主观感受由聚焦位置1到聚焦位置5, 清晰度依次上升. 实验结果表明选取的算法都只在聚焦位置5处达到极值, 满足单峰性要求; 转鼓图像清晰度计算结果与人眼的主观感受的图像清晰度变化一致, 满足无偏性要求; 除Tenengrad算法外, 其余算法计算结果均不相同, 且区分度较好, 满足灵敏性要求; 单次运行时间与表1相差不大, 每个算法对单张图片的运算时间都控制在1秒以内, 所以能够满足实时性要求.

|
图 11 亮度增强图像计算结果 |
3 结语
本文为了解决在传统裂隙灯转鼓装校生产线上, 由于人眼评价存在主观性和随机性等问题. 对当前较为常用的、具有代表性的几种基于空域的清晰度评价算法的原理定义和特点进行了详细的描述, 并搭建实验平台, 设计图像处理软件, 通过3组实验综合分析和对比了这算法对实际生产线上转鼓图像的适用情况. 结果表明除Tenengrad算法在灵敏性方面不能满足实际要求外, 其余4种算法都能满足要求. 而4种满足要求的算法当中, 又因为EVA算法在不同光照条件、不同放大倍率条件下所表现出更高的灵敏性, 能够区分轻微离焦状态, 更适合作为转鼓数字化装校系统图像清晰度评价算法而采用. 本文的研究可运用于实际的裂隙灯转鼓装校生产线, 以提高转鼓的装校质量.
| [1] |
Li YK, Yu TS, Li BX. Simultaneous event localization and recognition in surveillance video. 2018 15th IEEE International Conference on Advanced Video and Signal Based Surveillance. Auckland, New Zealand. 2018. 1–6.
|
| [2] |
Chandler DM. Seven challenges in image quality assessment: Past, present, and future research. ISRN Signal Processing, 2013, 2013: 905685. |
| [3] |
褚江, 陈强, 杨曦晨. 全参考图像质量评价综述. 计算机应用研究, 2014, 31(1): 13-22. DOI:10.3969/j.issn.1001-3695.2014.01.003 |
| [4] |
赵旦峰, 王博, 李明. 基于空域特征的无参考图像质量评价算法. 计算机工程与应用, 2016, 52(12): 216-220. DOI:10.3778/j.issn.1002-8331.1409-0232 |
| [5] |
Chen LL, Han M, Wan HL. The fast iris image clarity ev-aluation based on Brenner. 20132nd International Symposium on Instrumentation and Measurement, Sensor Network and Automation. Toronto, ON, Canada. 2013.
|
| [6] |
李祚林, 李晓辉, 马灵玲, 等. 面向无参考图像的清晰度评价方法研究. 遥感技术与应用, 2011, 26(2): 239-246. |
| [7] |
王健, 陈洪斌, 周国忠, 等. 改进的Brenner图像清晰度评价算法. 光子学报, 2012, 41(7): 855-858. |
| [8] |
Redondo R, Bueno G, Valdiviezo JC, et al. Autofocus evaluation for brightfield microscopy pathology. Journal of Biomedical Optics, 2012, 17(3): 036008. DOI:10.1117/1.JBO.17.3.036008 |
| [9] |
陈亮, 李卫军, 谌琛, 等. 数字图像清晰度评价函数的通用评价能力研究. 计算机工程与应用, 2013, 49(14): 152-155, 235. DOI:10.3778/j.issn.1002-8331.1202-0442 |
| [10] |
朱晨旭. DNA芯片电泳检测中的自动对焦和定位研究[硕士学位论文]. 南京: 东南大学, 2015.
|
| [11] |
崔作龙, 徐长松. 图像清晰度的量化测量探究. 实验技术与管理, 2012, 29(5): 49-51. DOI:10.3969/j.issn.1002-4956.2012.05.014 |
| [12] |
Trent1985. 无参考图像清晰度评价. https://blog.csdn.net/Trent1985/article/details/50904173, [2016-03-16].
|
| [13] |
王昕, 刘畅. 基于提升小波变换的图像清晰度评价算法. 东北师大学报: 自然科学版, 2009, 41(4): 52-57. |
| [14] |
潘雪娟, 朱尤攀, 浦恩昌, 等. 基于熵的自动聚焦图像清晰度评价函数仿真分析. 红外技术, 2016, 38(10): 838-844. DOI:10.11846/j.issn.1001_8891.201610005 |
| [15] |
徐贵力, 刘小霞, 田裕鹏, 等. 一种图像清晰度评价方法. 红外与激光工程, 2009, 38(1): 180-184. DOI:10.3969/j.issn.1007-2276.2009.01.039 |
| [16] |
王鸿南, 钟文, 汪静, 等. 图像清晰度评价方法研究. 中国图象图形学报, 2004, 9(7): 828-831. DOI:10.3969/j.issn.1006-8961.2004.07.011 |
| [17] |
魏红生, 何建农. 基于点锐度法和小波变换的图像融合方法. 计算机工程, 2010, 36(23): 204-206. DOI:10.3969/j.issn.1000-3428.2010.23.068 |
| [18] |
袁珂, 徐蔚鸿. 基于图像清晰度评价的摄像头辅助调焦系统. 光电工程, 2006, 33(1): 141-144. DOI:10.3969/j.issn.1003-501X.2006.01.034 |
| [19] |
范媛媛. 光测设备电视图像无参考质量评价方法的研究[博士学位论文]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2011.
|
 2019, Vol. 28
2019, Vol. 28


