计算机系统应用  2019, Vol. 28 Issue (9): 168-173   PDF    
引用本文
毛良献, 王品. 板材排样中非拟合多边形的构造实现方法. 计算机系统应用, 2019, 28(9): 168-173.http://www.c-s-a.org.cn/1003-3254/7061.html   
Mao LX, Wang P. Construction and Implementation of No-Fit Polygon for Packing and Cutting Problem. Computer Systems and Applications, 2019, 28(9): 168-173(in Chinese).http://www.c-s-a.org.cn/1003-3254/7061.html   
板材排样中非拟合多边形的构造实现方法
毛良献1,2, 王品2,3     
1. 中国科学院大学, 北京 100049;
2. 中国科学院 沈阳计算技术研究所, 沈阳 110168;
3. 沈阳高精数控智能技术股份有限公司, 沈阳 110168
收稿日期：2019-03-01; 修改日期：2019-03-29; 采用时间：2019-04-01; csa 在线出版时间：2019-09-05
基金项目：国家重大科技专项(2018ZX04035001)
通讯作者：毛良献, E-mail: 1029193287@qq.com.
摘要：非拟合多边形可用于处理两维的不规则形状的板材排样问题. 先前, 基于非拟合多边形的构造很难实现, 并且也没有通用的方式来处理多种特殊情况, 从而非拟合多边形并没有被广泛的使用. 本文介绍了一种基于环绕的实现方式来构造非拟合多边形, 对各种特殊情况能统一解决, 例如互锁, 交叉等. 通过对ESICUP的数据集测试, 表明该方法具有一定的效果, 可以对板材排样的解决思路提供一定的借鉴.
关键词: 板材排样    非拟合多边形    环绕方法    
Construction and Implementation of No-Fit Polygon for Packing and Cutting Problem
MAO Liang-Xian1,2, WANG Pin2,3     
1. University of Chinese Academy of Sciences, Beijing 100049, China;
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China;
3. Shenyang Golding NC & Intelligence Tech. Co. Ltd., Shenyang 110168, China
Foundation item: National Science and Technology Major Program (2018ZX04035001)
Abstract: The No-Fit Polygon (NFP) can be used for handling of stock packing and cutting problems with two-dimensional non-regular shape. Previously, NFP has not been widely applied because it is difficult to be implemented and is lack of generic approaches that can cope with all problem cases without specific case-by-case handling. This paper introduces an orbital method. The method can handle the typical degenerate cases, such as holes, interlocking concavities. And we make benchmark for ESICUP datasets which from the literature, proving that this approach can be efficient with almost every situation. It has certain reference significance for the research of the packing and cutting problem.
Key words: packing and cutting     no-fit polygon     orbital approach    

板材排样问题影响着许多领域, 例如纺织品、塑料、金属切削等等, 其中最主要的就是两维不规则形状的排样. 这些问题通常可以描述为: 将一系列的不规则的二维形状放置在一个或多个板子上, 使得他们尽可能的接触, 这样就可以节约板材的面积, 提高板材利用率. 这种板材排样是一个NP难问题, 因此有许多方法用于解决它, 包括线性规划方法, 启发式放置方法等等[1–4]. 通常, 绝大多数情况都可以利用三角函数[5]来解决, 但NFP提供了一种高效的解决策略.

在本文中, 介绍了非拟多边形及实现它一种方法. 非拟合多边形结构能处理一些传统方法(基于三角函数)很难解决的特殊情况, 说明非拟合多边形在排样处理中可以作为一种解决思路.

1 非拟合多边形

本文提出了一种非拟合多边形(No-Fit Polygon, NFP)的构造方式, 原理是利用环绕的方法来产生NFP[6], 该算法是对文献[6]提出的算法的一种改进实现. 比起传统的利用三角函数的重叠测试[7–10], 实现该算法简单, 同时具有时间复杂度较低的优点.

算法的原理如下, 输入参数是两个二维多边形, 形状可以是不规则的. 假定其中一个多边形(记为A)保持不动, 另一个多边形(记为B)绕A运动. 这样当B环绕A一周后, 就可以生成一个非拟合多边形(下面简称为NFP).

假定多边形A为固定多边形, B为环绕多边形. 算法实现过程分为4步. (1)首先需要A与B接触; (2)移动B; (3)找到下一个起点; (4)将平移向量合并.

1.1 多边形A与B的接触

在B绕A运动之前, 需要把B放置在A的边上, 保证B接触A, 但又和A不相交. 然后, 可以对B沿某方向平移, 使之一直是和A保持接触.

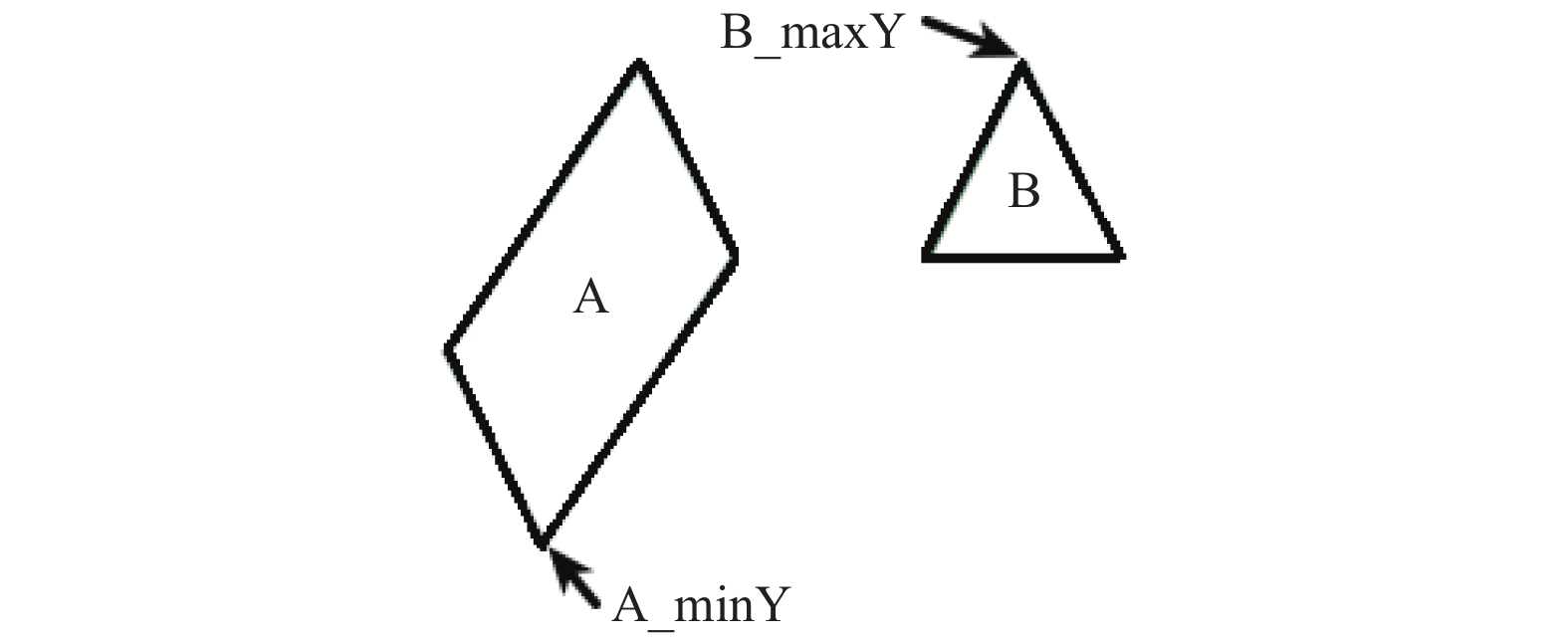
例如, 图1给出的多边形A和B, 同时标记了A的最低点A_minY和B的最高点B_maxY.

图 1 多边形A和B

那么, 可以让B的最高点与A的最低点接触, 这样A与B是一定接触, 但不相交(也可以有其他方法, 例如B最左点和A的最右点接触, 等等). 平移向量

$\rm{{\overrightarrow {\rm{T}}} = A\_\min Y - B\_\max Y}$ (1)

那么B按T平移后, 如图2所示, B与A接触并且不交叉. 此时, B所在位置是B绕A运动的开始位置, 并记录起点和B的参考点, 保证B在绕A平移过程中可以回到初始位置. 设B的参考点和起点都为A_minY. 那么, 当B的参考点再次平移到起点(A_minY)时, 就可以确定B绕A一周.

1.2 移动B

在A与B接触后, 需要对B做平移操作. 这个过程细分为以下5步.

1.2.1 找出接触边对

当前A和B接触, 通过遍历A和B的全部边, 找出所有接触点. 继而确定全部接触边对.

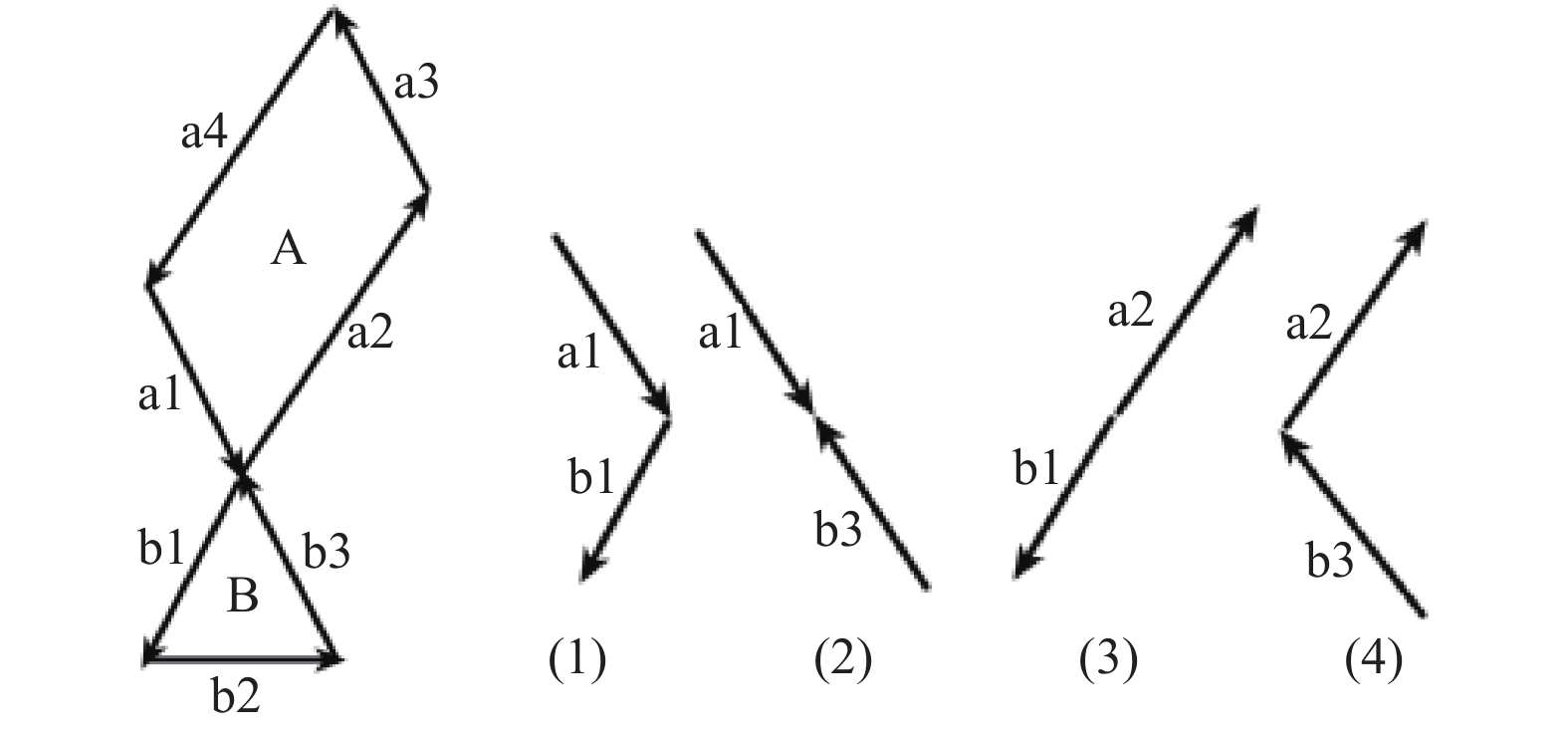
如图3所示, 找到4组接触边对, 分别是<a1, b1>, <a1, b3>, <a2, b1>, <a2, b3>.

图 2 多边形B沿T向量平移

图 3 接触点及接触边对

1.2.2 从接触边对中找出平移向量

在1.2.1节中, 找到4组接触边对. 接触边对的作用是: 一组接触边对能生成一个平移向量, 故能得到全部的平移向量. 例如, 在图3的4组边对中, 1号边对<a1, b1>可以生成一个平移向量 $\overrightarrow {\rm{T}} = - \overrightarrow {{\rm{b}}1} $ , $\overrightarrow {\rm{T}} $ 是由边b1生成的. 那为什么是由边b1生成, 而非a1生成? 算法假定平移向量是接触点到边的终点, 故a1生成的是空向量. $\overrightarrow {\rm{T}} $ 是 $\overrightarrow {{\rm{b}}1} $ 的反向, 这是认为B必须绕A做逆时针运动. 那么2号边对<a1, b3>就不能生成平移向量. 因为接触点是a1(也是b3)的终点. 而3号边对<a2, b1>(a2与b1是平行关系)可以生成平移向量 $\overrightarrow {\rm{T}} = \overrightarrow {{\rm{a}}2} $ (或者 $\overrightarrow {\rm{T}} = - \overrightarrow {{\rm{b}}1} $ ). 也就是说, 在这种情况下可以选择任何一边来生成平移向量. 4号边对<a2, b3>中, $\overrightarrow {\rm{T}} = \overrightarrow {{\rm{a}}2} $ . 接触边对对应的平移向量见表1.

1.2.3 删除不可行的平移向量

对1.2.2节中找到的所有平移向量, 需要依次判断多边形A与B这些向量移动会不会交叉. 若有交叉, 那么该向量就是不可行的. 按如下方式思考: 因为B绕A运动, 那么1.2.1节中的接触边对中来自B的边是运动的. 也就是说, 我们可以对每一个平移向量, 依次针对每一组接触边对, 判断来自B的边按该向量平移, 是否与来自A的边相交. 若有一组接触边相交, 那么就可以判断该平移向量是不可行的, 直接舍弃.

表 1 多边形A和B的接触边对对应的平移向量

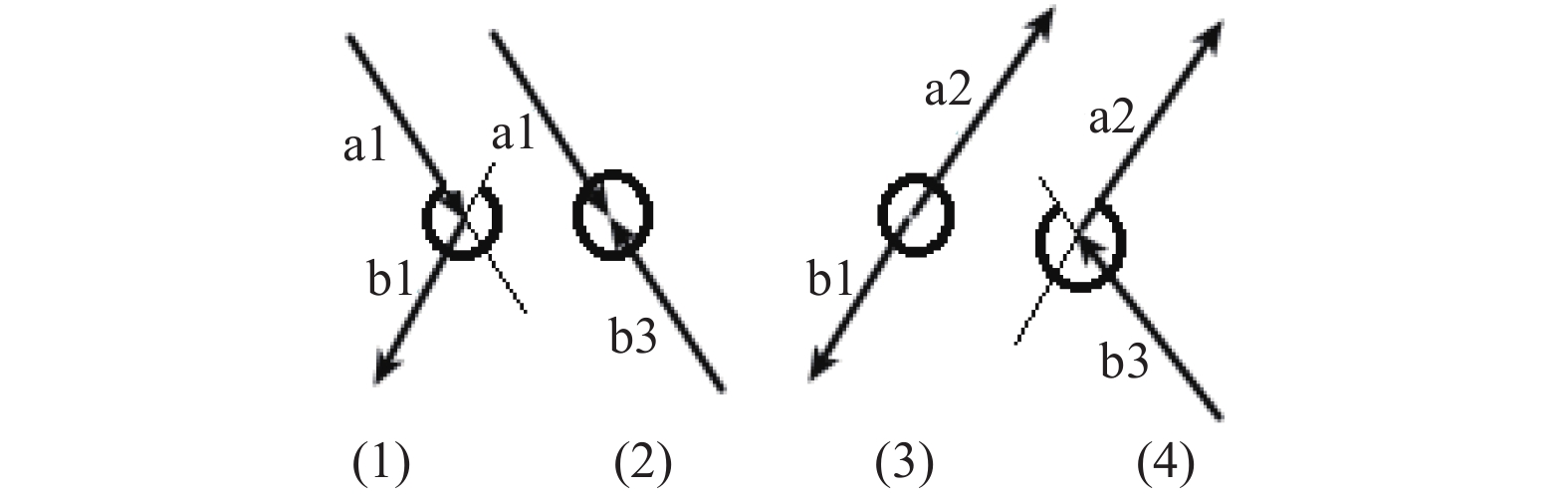
那么怎么验证接触边对中来自B的边按平移向量平移, 会不会与来自A的接触边交叉. 对于每一组接触边对而言, 可以计算出弧度区间, 使得来自B的边沿区间中的某个弧度方向平移, 不会和来自A的边相交. 故只需要判断平移向量的弧度方向是否在该区间内即可. 例如, 对1.2.1节中的四组接触边对, 可以确定相应的弧度区间(用圆弧表示可行的弧度区间, 如图4所示.

图 4 接触边对的可行弧度区间

在1.2.2中, 找到的平移向量有 $ - \overrightarrow {{\rm{b}}1} $ 和 $\overrightarrow {{\rm{a}}2} $ . 对照4组接触边对的弧度区间和 $ - \overrightarrow {{\rm{b}}1} $ (或 $\overrightarrow {{\rm{a}}2} $ )的弧度方向, 发现 $ - \overrightarrow {{\rm{b}}1} $ (或 $\overrightarrow {{\rm{a}}2} $ )的弧度方向均在每一组的弧度区间内, 故 $ - \overrightarrow {{\rm{b}}1} $ 和 $\overrightarrow {{\rm{a}}2} $ 都是可行的平移向量.

1.2.4 修剪可行的平移向量

通过1.2.3的过滤, 找到了全部可行的平移向量. 那么接下来, 需要判断每一个可行的平移向量是否能全部应用.

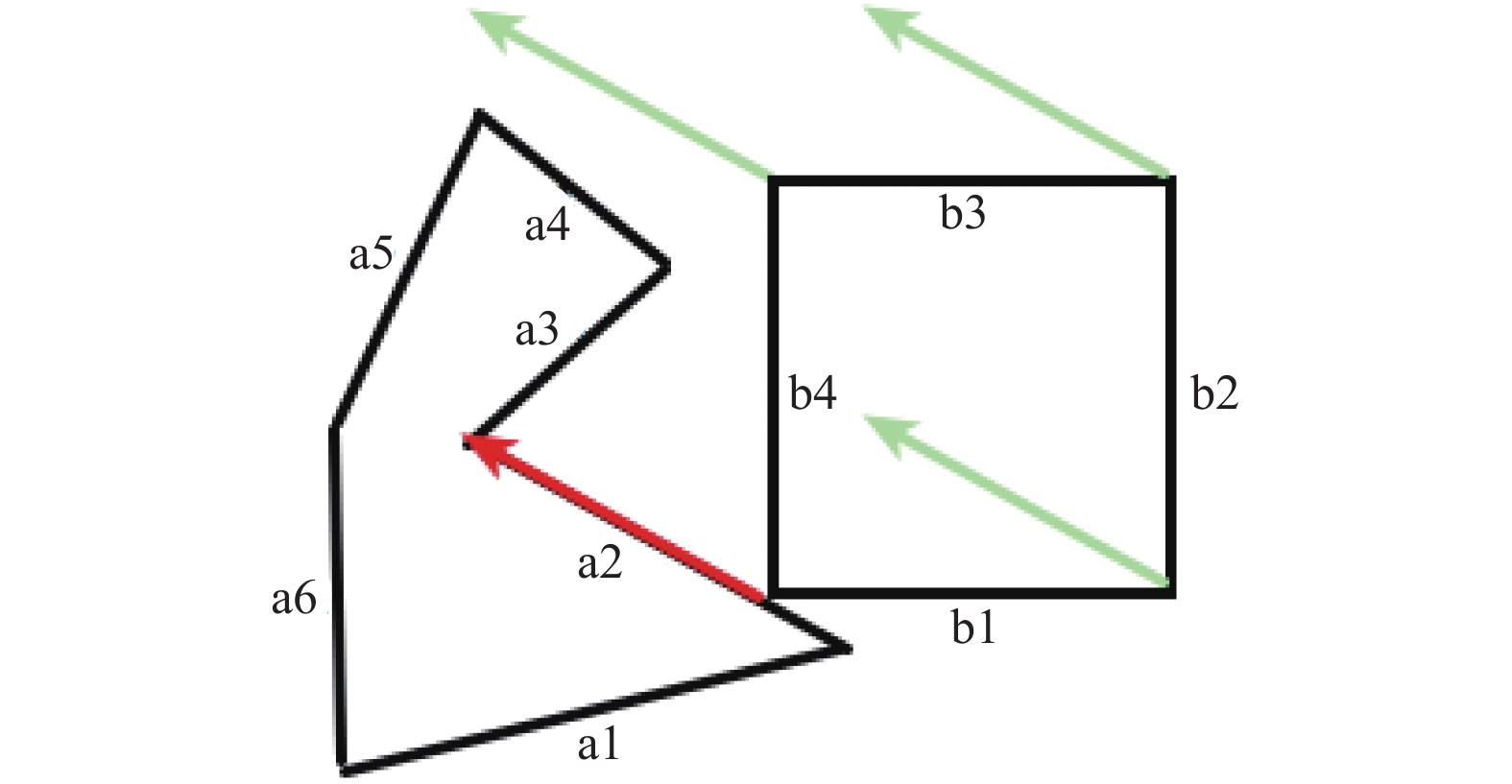
在图5中, A是一个不规则多边形, B是一个矩形. 红色的是一个可行的平移向量, 浅绿色是红色的平移向量平移到B的每个顶点之后的情况.

此时B沿着红色的平移向量平移, A与B必然交叉. 从而, 必须对红色向量进行修剪. 图中得到修剪后的是绿色的平移向量. 看到有两个绿色向量, 但取得是较短的那个. 同时, 需要注意的是, B按修剪后的平移向量平移, 一定不会与A相交?

图 5 多边形沿平移向量平移, 交叉

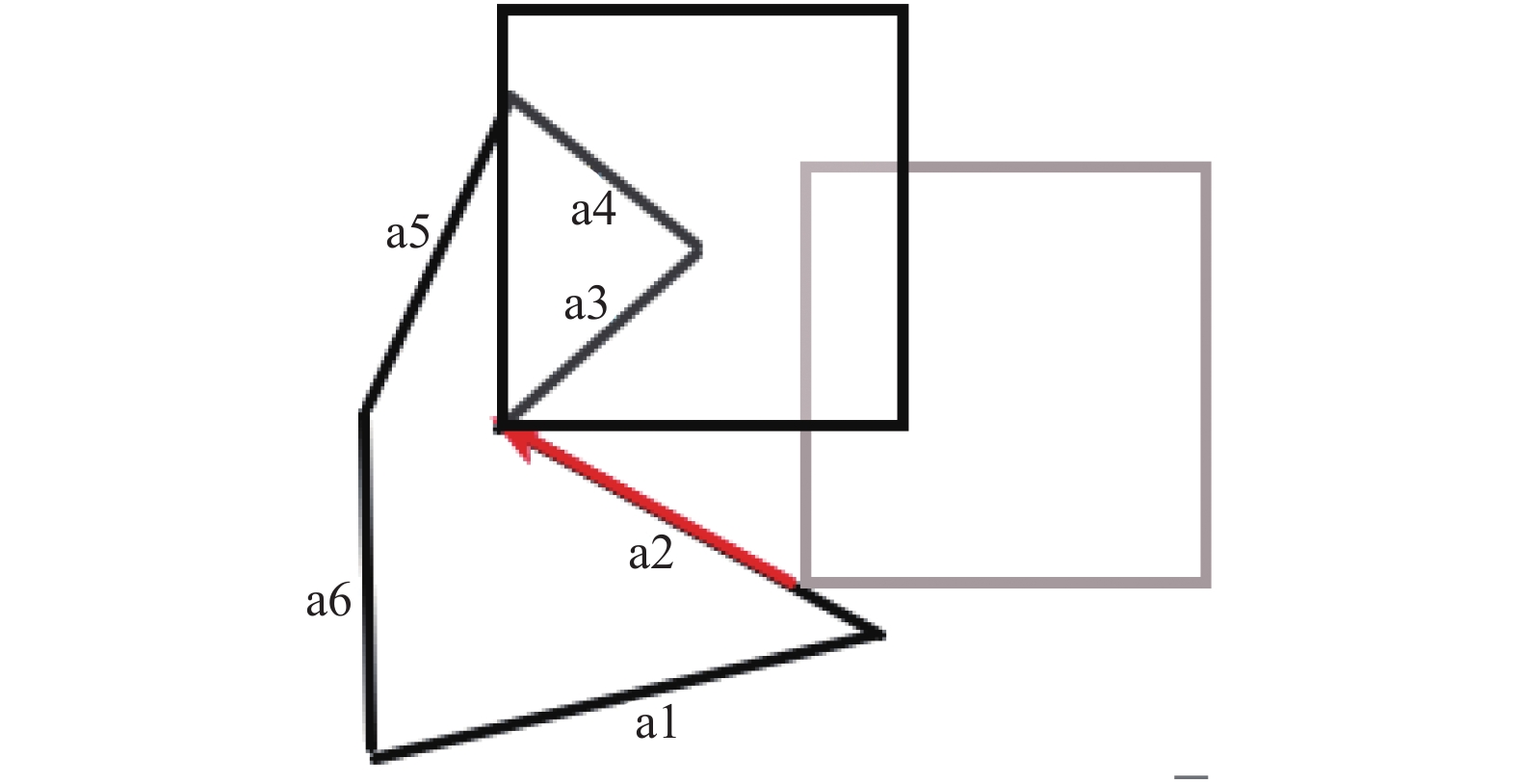
在图6中, A不变, B是较大的矩形, 红色向量仍是可行的平移向量. 将红色向量平移到B的每个顶点, 发现并不需要修剪平移向量. 但是按红色向量平移后, 如图7所示, A与B相交. 这种情况下, 就需要考虑将可行的平移向量平移到A的每个顶点, 然后再修剪. 如图8所示.

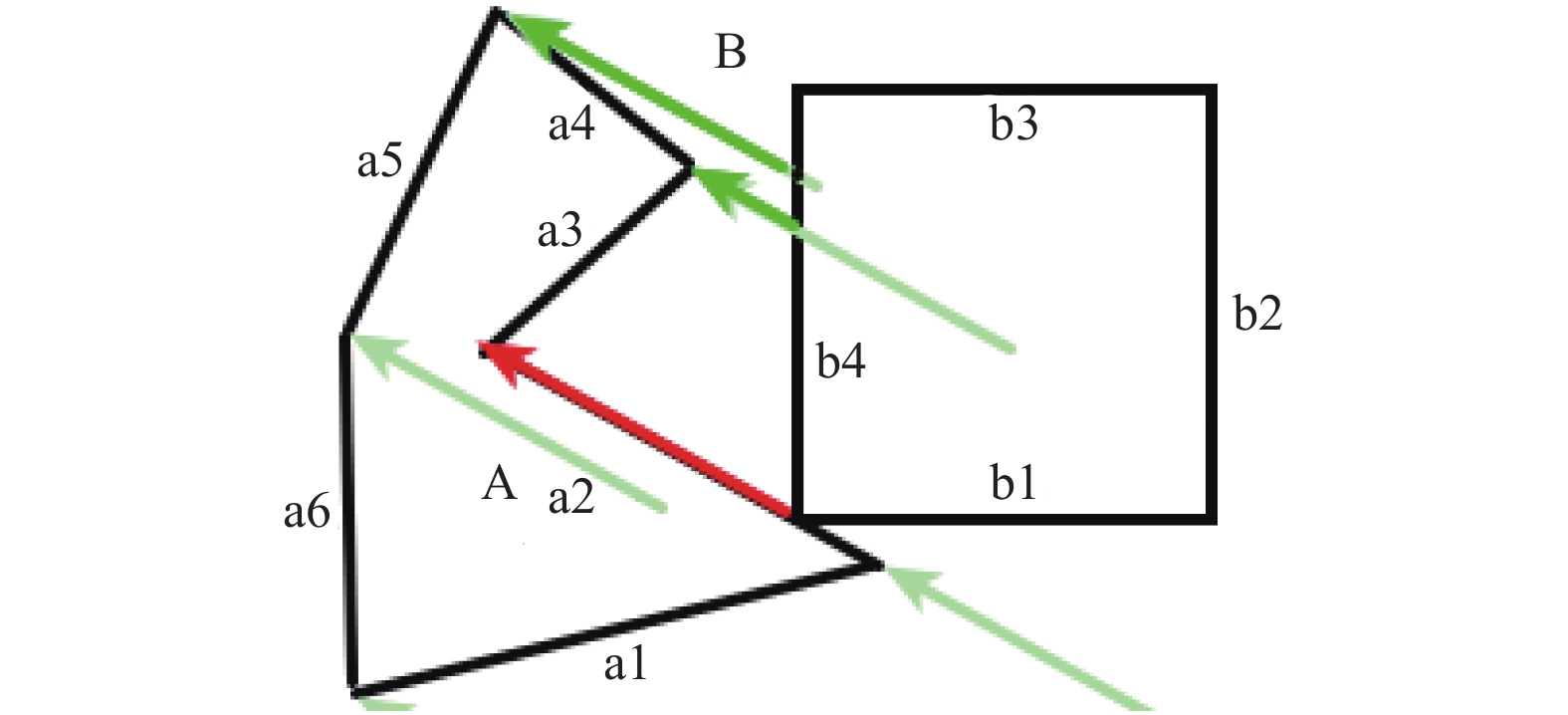
在图8中, 将平移向量的每个终点平移到A的每个顶点, 判断与B的交叉性, 最终得到修剪后的平移向量(绿色). 然后将两种情况的最小值作为最终的可行平移向量. 对每一个可行的平移向量执行上述过程之后, 就能得到全部修剪后的平移向量, 然后按从长到短排序. 接下来只需要按最长的修剪后的可行平移向量平移B就可以了.

图 6 平移向量的起点放置在B的每个顶点

图 7 多边形B沿平移向量平移

图 8 平移向量的修剪

值得指出的是, 在文献[5]中, 直接使用修剪后的最长平移向量进行平移. 但是, 在实验中发现该平移向量不一定是能用的. 也就是说, 按此平移向量平移后, B在下一次平移之前就不一定与A接触了.

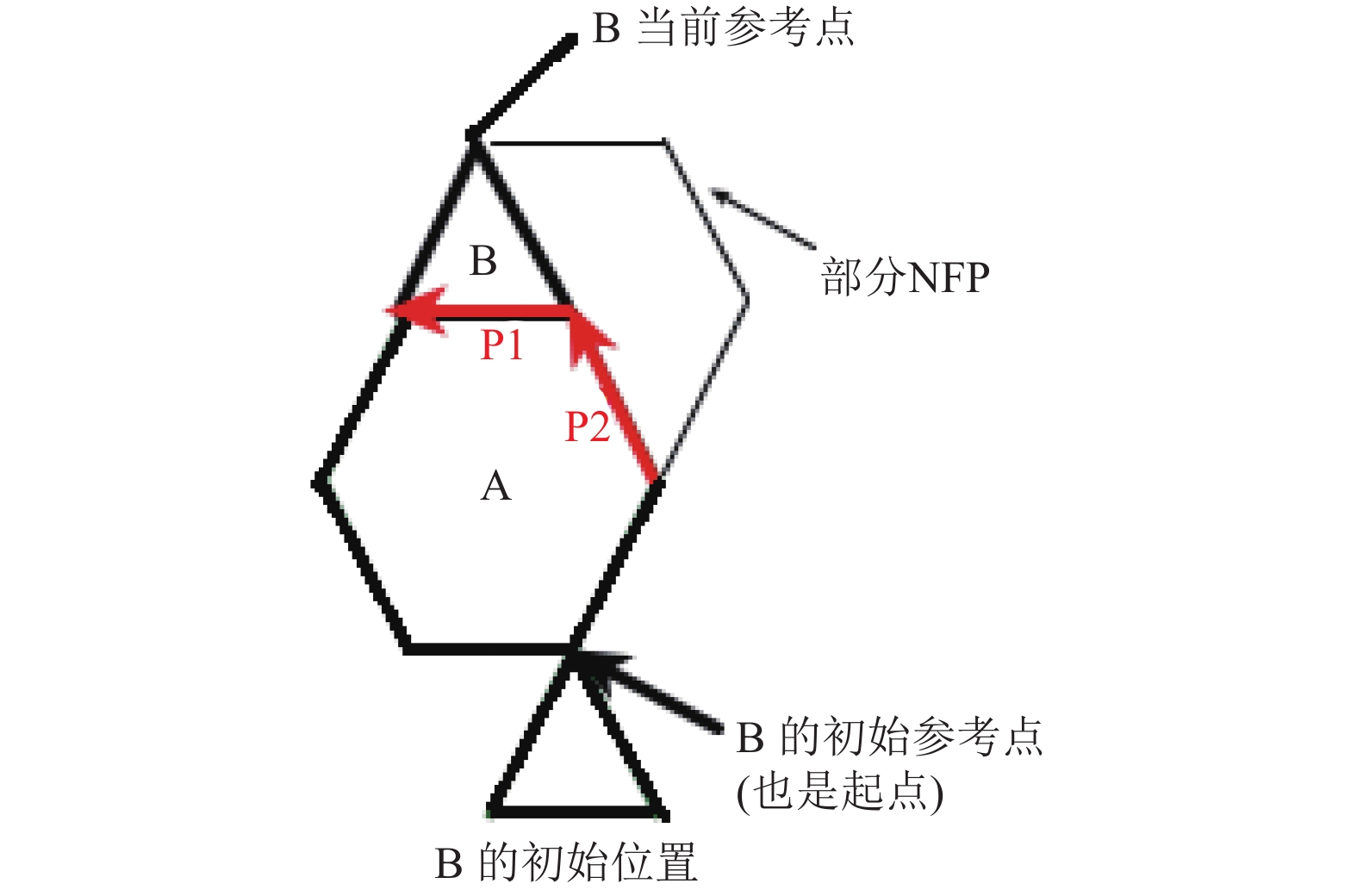
在图9中, 找到了两个可行的平移向量 $\overrightarrow {p1} $ 和 $\overrightarrow {p2} $ , $\overrightarrow {p2} $ 的长度比 $\overrightarrow {p1} $ 的长, 并且 $\overrightarrow {p1} $ 和 $\overrightarrow {p2} $ 均是不需要修剪的. 当B按 $\overrightarrow {p2} $ 平移之后, A与B就不在接触, 那么在下一轮找接触点时, 就不可能找到, 也就无法继续执行. 因此, 在此种情况下, 需要抛弃 $\overrightarrow {p2} $ , 选择 $\overrightarrow {p1} $ .

1.2.5 移动多边形B

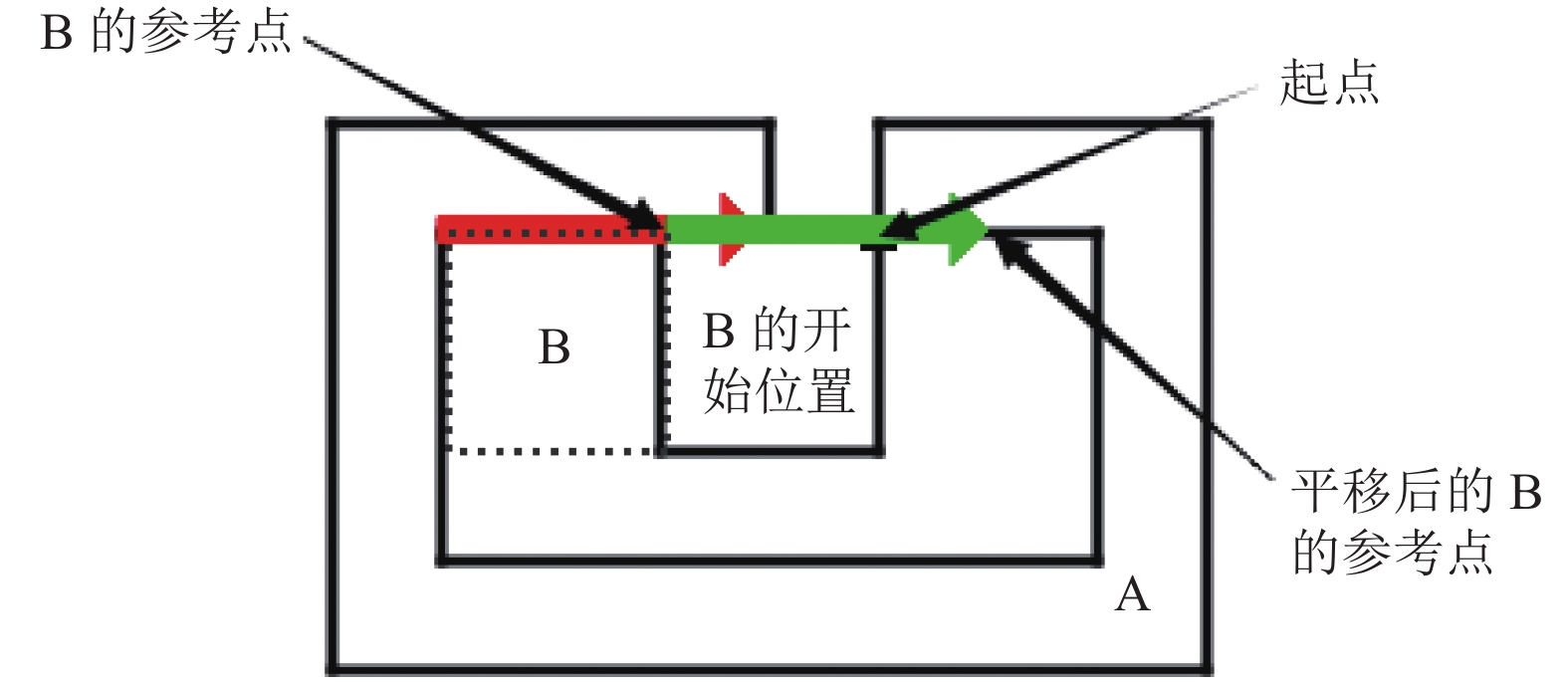
通过前面的步骤, 得到了修剪后最长的可行平移向量. 接下来, B按这个向量平移即可. 但需要注意两点: (1)判断B的参考点是否回到了起点. 若回到起点, 得到一个NFP. (2)判断B的参考点是否越过起点. 这个是对文献[5]的一个补充. 也就是此时B的平移距离过长, 超过了起点, 如图10所示.

图 9 B沿平移向量 $\overrightarrow {p1} $ (或 $\overrightarrow {p2} $ )平移情况分析

图 10 B的参考点沿平移向量平移越过起点

在图10中, 红色的是可行的平移向量, 绿色的表示B的参考点的平移. 由图知, 当B的参考点沿平移向量平移后, 越过了起点. 本来可以生成一个NFP, 现在就会无限循环下去, 因为B的参考点不会移东到起点了. 在这种情况下, 需要缩短平移向量.

1.3 找到下一个起点

在1.2节中, 生成了一个完整的外部NFP, 是B对A的外部环绕. 是否存在着其他NFP呢? 也就是B在A的内部平移存不存在, 从而生成内部的NFP. 这里涉及到起点搜索. 在1.2节中, 我们假定的起点是A的最低点. 而在这里, 我们需要找到其他起点, 以便B能从这些起点出发, 得到其他的NFP.

1.3.1 起点搜索算法

在寻找外部NFP过程中, A中的有些边可能没有遍历到. 故可以从这些边中寻找起点. 假设a是A中一条未遍历的边, 试着在a中找到一个可行的起点. 算法过程如下: 依次让B的每个顶点平移到a的起点, 判断: (1)如果A此时与B没有相交, 那么a的起点是一个可行的起点. 可再次运用1.2节中介绍的方法. (2)如果A此时与B有交叉, 那么需要让B沿着a移动, 直到平移到一个的不相交位置, 或者到达a的终点(这就说明在a上不可能找到起点).

现在, 假定A与B相交, 然后B沿a平移寻找可行的起点. 首先, 可以快速判断一下, B沿着a移动是否一定存在交叉. 方法如下: 因为此时的接触点是a的起点, 并且B中有两条边也接触到这个顶点. 那只要判断一下, B的两条接触边是否至少有一条边在a的左侧. 若成立, 那么B沿着a移动一定会与A相交. 这样, 就需要判断A中其他未遍历的边了. 如果通过上述判断, 就需要修剪a向量. 过程如下: 当前的平移向量 $\overrightarrow T $ =a的起点->a的终点. 同样, 利用1.2.4中介绍的修剪方法修剪 $\overrightarrow T $ , 得到 $\overrightarrow {T'} $ . 那么B按 $\overrightarrow {T'} $ 平移, 同时更新接触点和B的参考点. 再次运用1.2节中介绍的方法, 找出剩余的平移向量. 这里要注意, 就是对a进行标记, 表示a被遍历过了. 那么在下一次的搜索中就不会遍历边a了.

1.4 平移向量合并生成NFP

通过1.1节到1.3节的计算, 找到所需要的全部平移向量. 现在, 就需要对他们合并生成NFP. 每一组平移向量都对应一个起点和B的参考点. 那么对B的参考点执行一组平移操作, 就可以生成一个NFP.

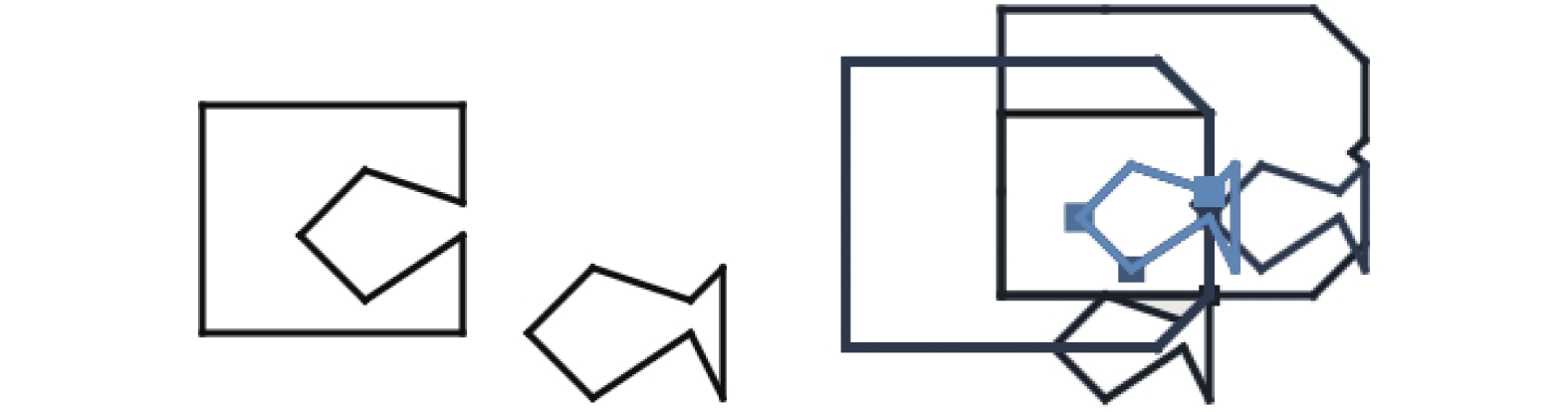
2 案例介绍

下面举一些例子,如图11至图15, 表明算法的运行情况. 图11至图15中左图是多边形的初始位置, 右图是平移的开始位置、起点和生成的NFP.

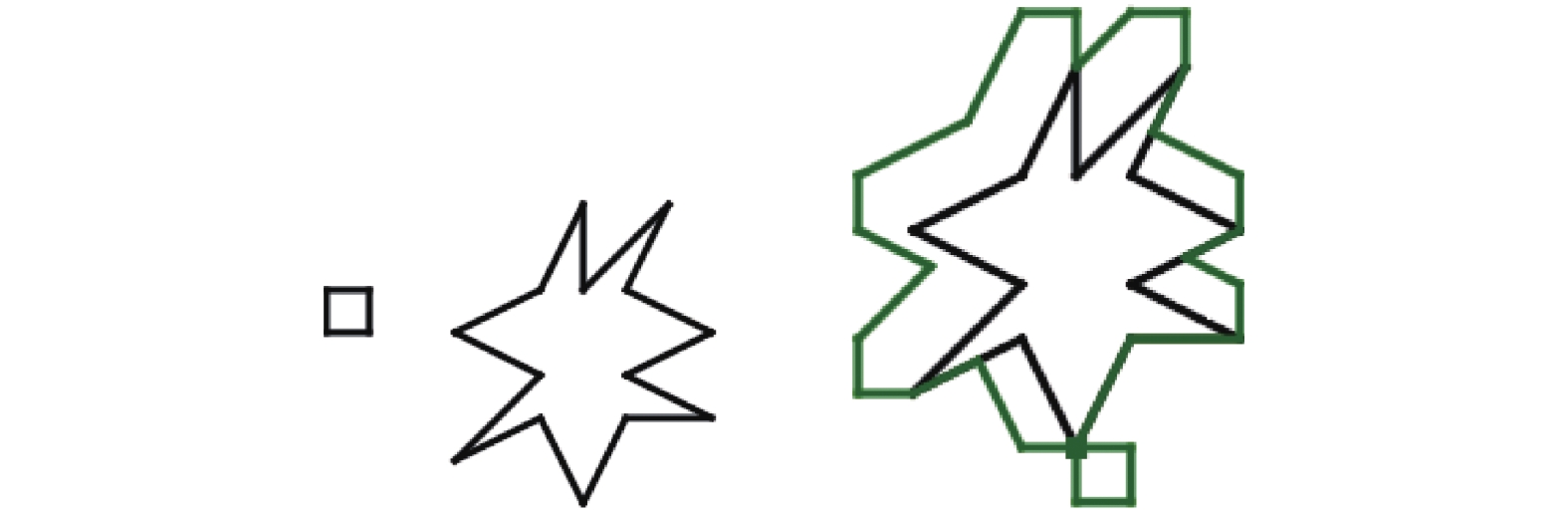
图 11 生成一个外部的NFP

3 测试

根据文献[5]和来自the Association of the European Operational Research Societies的板材排样工作小组的数据集(https://www.euro-online.org/websites/esicup/data-sets/), 执行如表2所列出的测试. 实验中使用的机器为Intel Core i5-3230M@2.6 GHz, 8 GB内存. 表格的形式参考了文献[5].

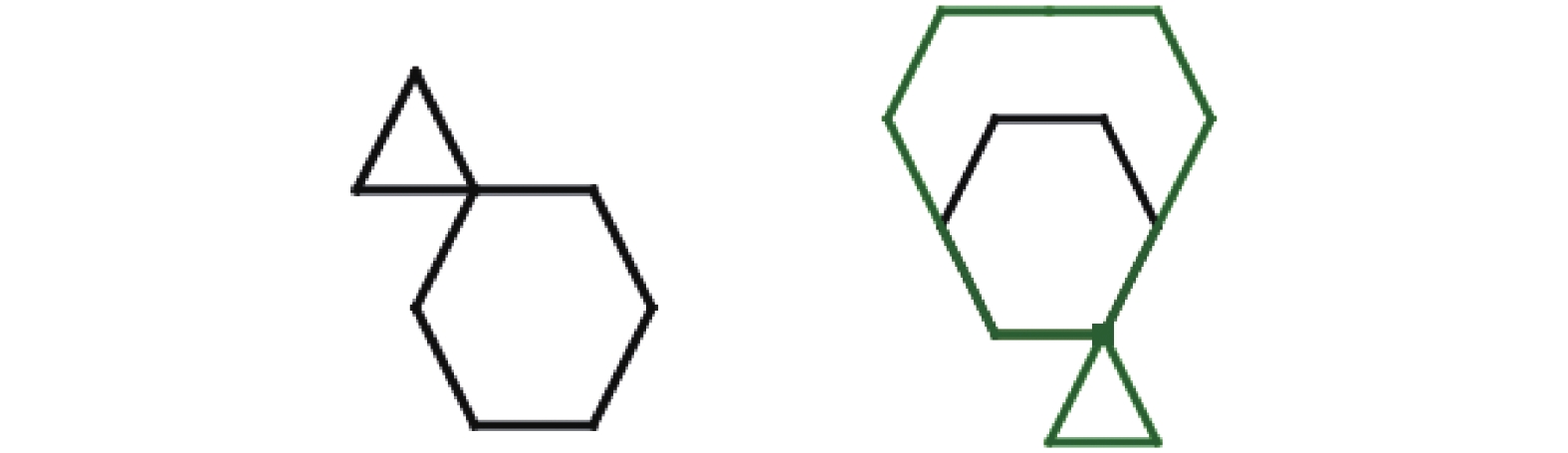
图 12 生成一个外部的NFP

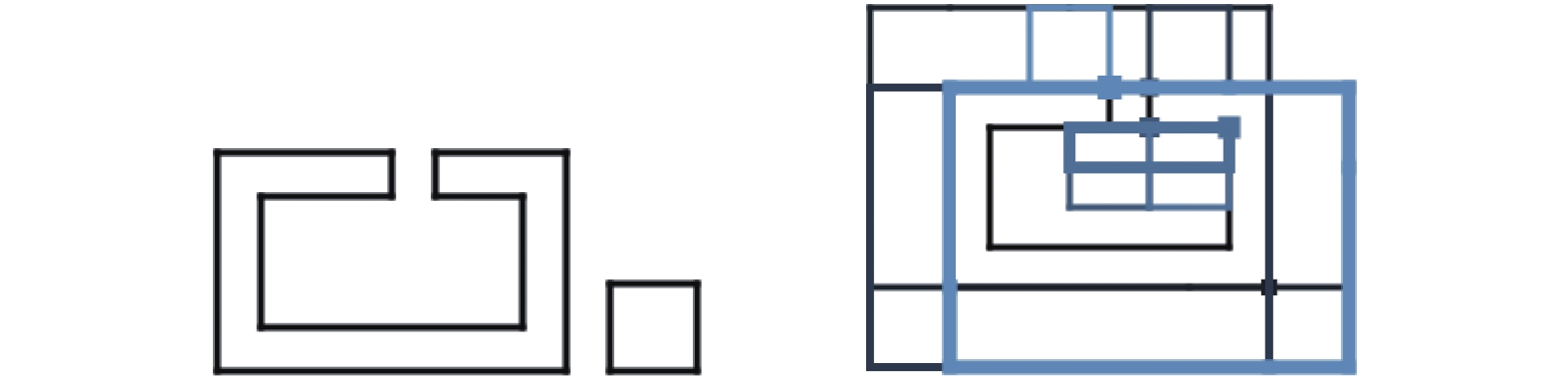
图 13 生成内部和外部的NFP

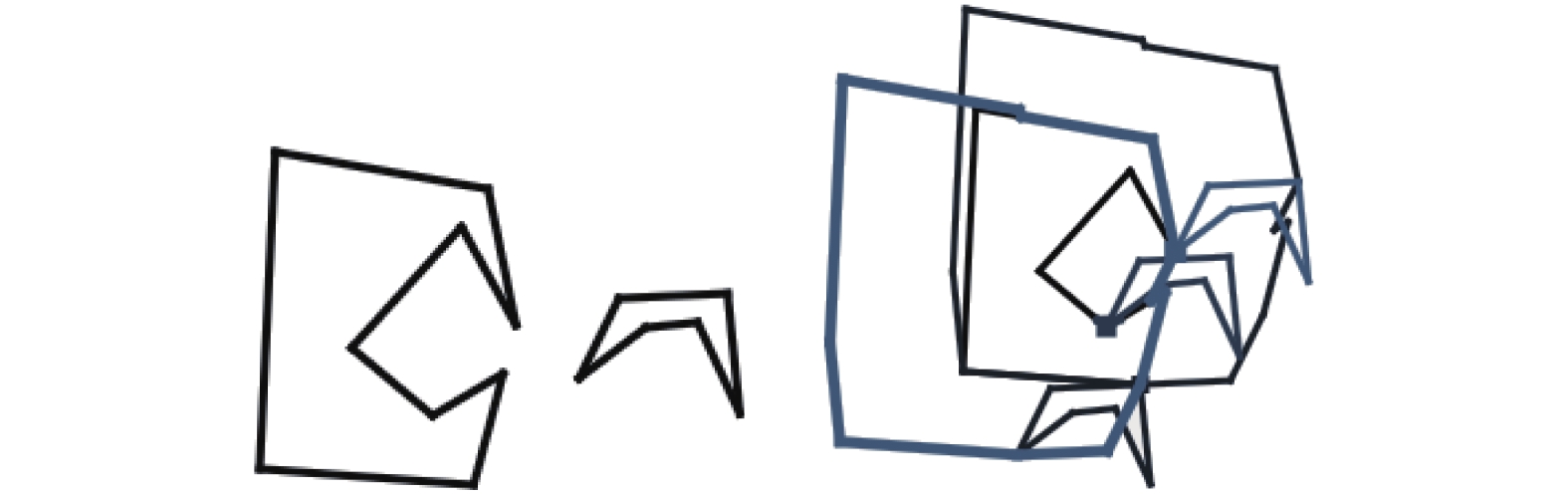
图 14 生成内部和外部的NFP

图 15 互锁和外部的NFP

4 结论与展望

生成了完整的NFP结构, 给出算法实现的具体细节和一些要点. 通过测试, 表明该方法具有一定的高效性. 与先前的一些借助于三角函数的方法相比, 该算法的实现简单, 高效, 且不需要对每一种特殊情况做特殊的考虑. 利用起点搜索过程, 对某些传统方法无法解决的互锁, 洞等情况, 能够成功解决. 对板材排样系统的设计与实现有一定的借鉴意义.

表 2 对不同数据集的测试结果

参考文献
[1]
贾志欣, 殷国富, 罗阳. 二维不规则零件排样问题的遗传算法求解. 计算机辅助设计与图形学学报, 2002, 14(5): 467-670. DOI:10.3321/j.issn:1003-9775.2002.05.020
[2]
李建涛, 黄星梅, 钟志华. 二维矩形件切割的路径优化. 机械设计与制造, 2005(4): 86-87. DOI:10.3969/j.issn.1001-3997.2005.04.040
[3]
王书文, 黄星梅, 李建涛. 二维矩形件组块优化切割的研究与实现. 苏州大学学报(工科版), 2007, 27(6): 49-52.
[4]
曹德列. 不规则图形数控切割关键技术研究[硕士学位论文]. 武汉: 华中科技大学, 2012.
[5]
O’Rourke J. Computational Geometry in C. 2nd ed. New York: Cambridge University Press, 1998.
[6]
Burke EK, Hellier RSR, Kendall G, et al. Complete and robust no-fit polygon generation for the irregular stock cutting problem. European Journal of Operational Research, 2007, 179(1): 27-49. DOI:10.1016/j.ejor.2006.03.011
[7]
Bennell JA, Dowsland KA, Dowsland WB. The irregular cutting-stock problem - A new procedure for deriving the no-fit polygon. Computers & Operations Research, 2001, 28(3): 271-287.
[8]
Dowsland K A, Dowsland WB. Packing problems. European Journal of Operational Research, 1992, 56(1): 2-14. DOI:10.1016/0377-2217(92)90288-K
[9]
Agarwal PK, Flato E, Halperin D. Polygon decomposition for efficient construction of Minkowski sums. Computational Geometry, 2002, 21(1-2): 39-61. DOI:10.1016/S0925-7721(01)00041-4
[10]
Art Jr RC. An approach to the two dimensional irregular cutting stock problem. Massachusetts: IBM Cambridge Scientific Centre, 1966.